基于包络矩形算法的实战连续射击技能评价

何移宸，周维方，叶强

(1. 南京体育学院体育教育与人文学院，南京 210014；2. 南京森林警察学院特警学院，南京 210023)

0 引言

射击技能评价是帮助射手找到自身问题、提高成绩的重要指标，也是指导训练和教学的重要依据[1]。日常实战射击训练中主要采用靶弹着点命中环数和依靠环数评定等级的方法，这种方法侧重射击准确性评价，然而对于不规律持续射击、多发速射等模拟实战环境的射击训练而言，无法反映射手连续射击的技术稳定性和一致性[2]，也难以提取综合、有效的信息指导射手技术改进训练。为了适应近距离非线性作战发展，射击实战化训练依靠大量实弹练习来提高射击技术的模式不仅损耗巨大，效果也不明显，甚至导致训练损伤，因此原有射击效果评价方法难以满足面向实战指导思想下的射击训练发展。

针对传统命中环数方法对射击稳定性评价不足的问题，研究多从弹着点散布误差或密集度检测分析寻求解决方法，常见检测方法包括：基于统计学习方法的云模型方法[3]、基于离散中心距离误差的散布域方法[2]、基于散布误差分析的统计模拟法[4]等。这些方法多用于导弹、火炮、枪械等器械火力密集程度评价，需要大样本的弹着点数据集，对于小样本弹着点数据集的手枪、自动步枪等射击技能评价，基于弹着点散布包络特征的检测方法仍然是较适宜的选择[5-6]。本文从分析弹着点散布面积计算着手，提出一种新的实战连续射击技能评价方法，能用于快速进行射击准确性和稳定性综合评价。

1 弹着点散布面积的评价方法

呈现于靶纸上的弹着点散布可以表达为给定二维平面上的点集，相关包络及其特征分析方法包括最小凸包法[7]、包络圆法[8]和包络矩形法[9]三种(表1)。

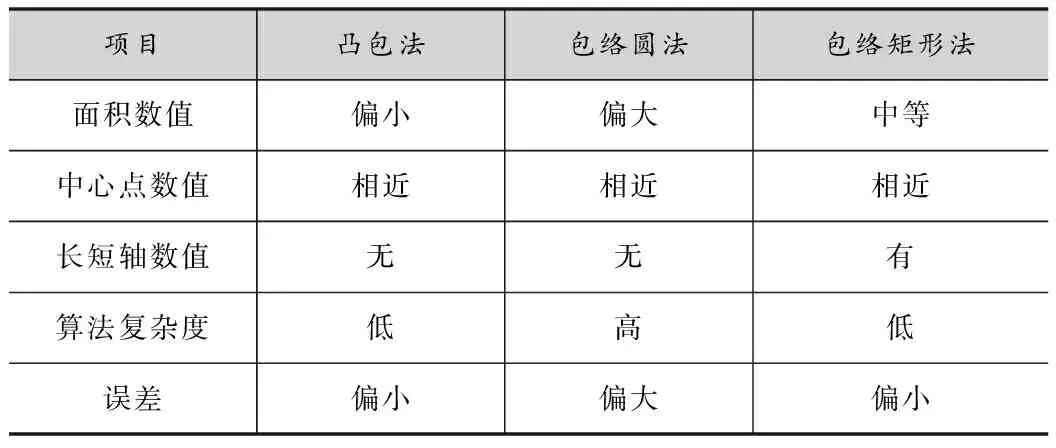
表1 方法比较

凸包是一个计算几何的概念，是在二维平面上将所有最外侧散点连接起来的一个凸多边形，它能够可以涵盖所有的散点，从而计算其面积并判断图形中心得到需要的数据。处理前需输入所有坐标点，找出输入数据中所有X轴坐标和Y轴坐标中最大及最小值的四个点，并删除所构筑四边形中所有的点。然后按Y轴坐标数值进行排序，并删除共线的点，对X轴数值进行定向，确定计算方向后按顺时针或逆时针方向进行运算，得到相应的图形，面积及其几何中心。

包络圆是指通过一个最小的标准圆来包含所有数据散点的图形，其圆周最少需要通过两个或两个以上的散点。处理前需输入坐标点集大于3的所有坐标点，而后根据如示函数公式初步计算包络圆圆心及包络圆半径，遇到不可计算点集则代入算法，通过三点求圆算法及其函数公式进一步确定包络圆圆心及包络圆半径，从而计算包络圆面积，包络圆圆心即所需坐标散点中心点坐标。

包络矩形是指将所有数据散点可以用一个矩形完全覆盖，其四个顶点及其四边上分别需要经过最少一个散点。在处理前同样需输入样本坐标点集数大于3的坐标点集，通过算法构建包络矩形，得到包络矩形四个顶点坐标数值，从而计算出包络矩形的面积和中心点坐标，同时得到所需包络矩形长短轴长度数值。

随机生成一组含五个弹着点的数据集，分别用三种方法进行模拟(图1)。通过对比发现，三种算法在中心点数值上具有相关性，射击准确性的评价上三种方法没有显著差异。通过散布面积反映密集程度用于稳定性评价时，包络矩形法与最小凸包法在算法复杂度和误差上较低，而包络圆法最高，同时因为数据集的小样本量特征，包络圆法所提取散布区域面积值偏大，不适用于描述单轮次射击弹着点散布范围。尽管凸包法能获得最小的散布区域面积，而包络矩形法数值略高于凸包法，但通过因子分析发现，包络矩形法的面积数值足以反映射手射击弹着点的散布范围，同时包络矩形法能反映散布区域的方向性特征，用于描述射击弹着点的具体偏移方向及偏移量，信息利用率最高，有利于进一步解读射手的射击技术和射击习惯，从而更好地对射手训练给予指导意见。由于最小包络矩形算法具有方便计算、数值详尽、误差较小等优势，为此本文使用最小包络矩形算法用于实战连续射击技能评价方法构建。

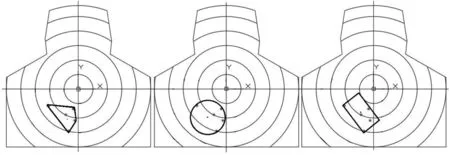
图1 模拟结果对比(左最小凸包法，中包络圆法，右包络矩形法)

2 最小包络矩形算法

2.1 数据采集

对原始胸环靶纸进行图像转换，经坐标比例转换，转换后坐标原点为靶中心点，坐标比例为1:20，逐一对靶纸上弹着点进行采样，获得原始弹着点中心横坐标和纵坐标向量Xi和Yi。实际过程中单轮次最小射击数目为5，在射手不脱靶情况下可以保证算法如期运算。若出现脱靶现象，则该轮次射击成绩不作为实验数据使用。

将坐标点集输入包络矩形算法中，判断输入样本坐标点集数是否大于3，确定输入点集能够构建包络矩形，并得到输入点集的最小凸包坐标。若坐标点数目小于3，则返回前端，不进行运算。

2.2 最小矩形提取

将坐标点的横，纵坐标作为算法的输入。如果坐标点的个数小于等于4，则无法构成一个矩形。若坐标点个数大于3则计算输入点集的最小凸包的坐标。

在上一步基础上获得的凸包的边按逆时针排列依次为l1，l2， …，lm-1，其最小包络矩形算法处理步骤如下：

步骤1：选择凸包一条边l1，计算此边与x轴的夹角θ；

步骤2：利用公式(1)计算旋转后各顶点的坐标，找出Xmin、Xmax、Ymin、Ymax；

x'=xcosθ+ysinθ

y'=-xsinθ+ycosθ

(1)

步骤3：利用公式(2)计算包络矩阵长L、宽W以及面积S。

L=xmax-xmin

W=ymax-ymin

S=L×W

(2)

重复步骤1-3，直至遍历完凸包每一条边，得到n个包络矩形，并选择面积最小的作为最小包络矩形。其中(x，y)为构成最小凸包的坐标，(x′，y′)为坐标转换后各顶点坐标。

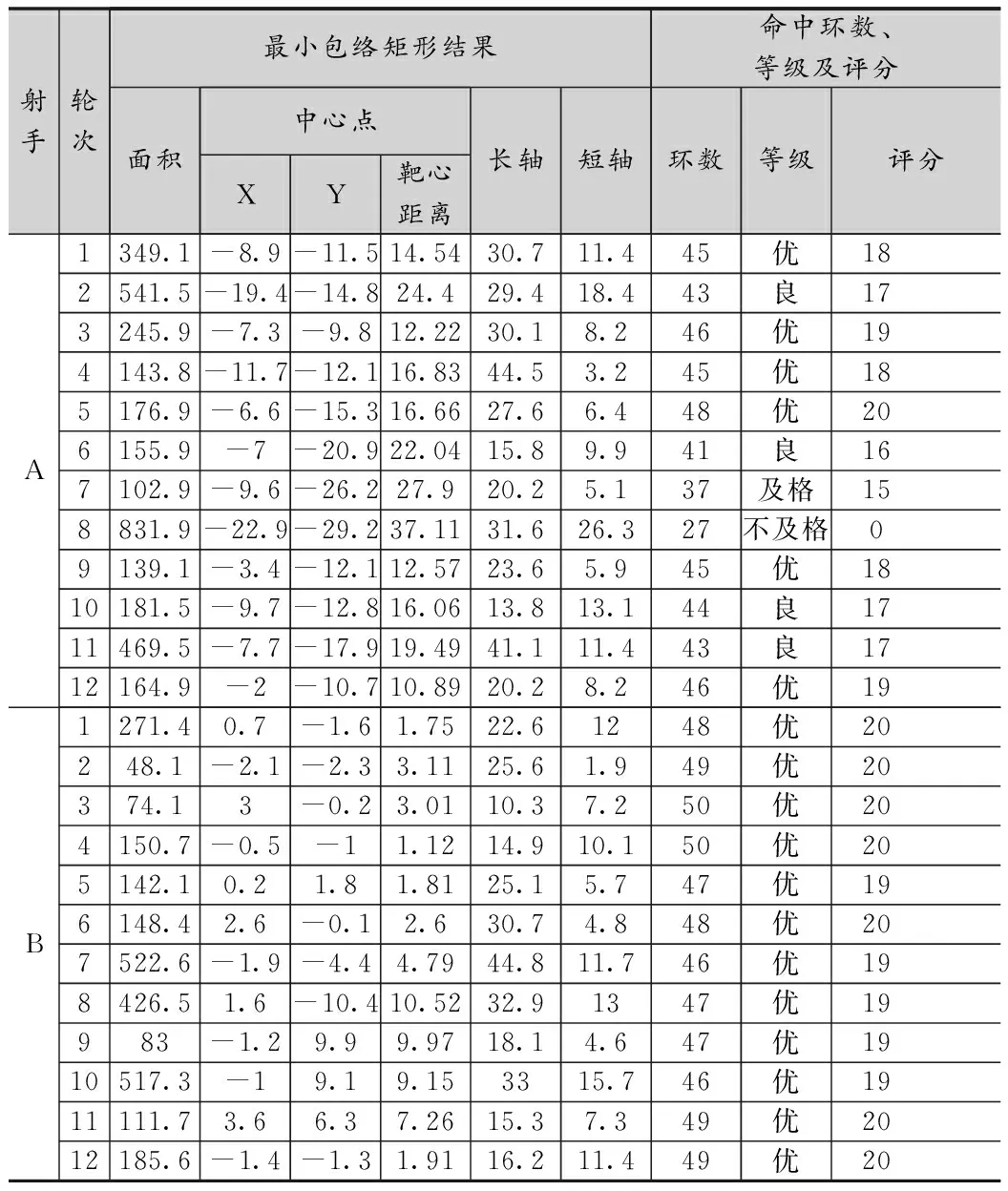
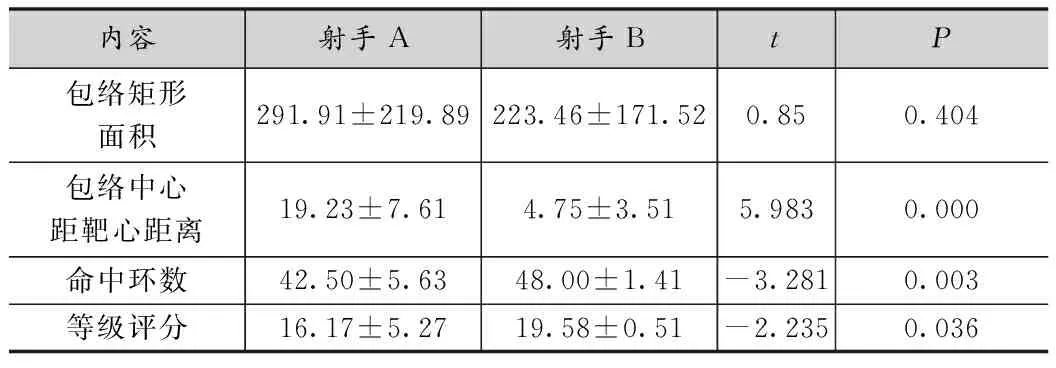
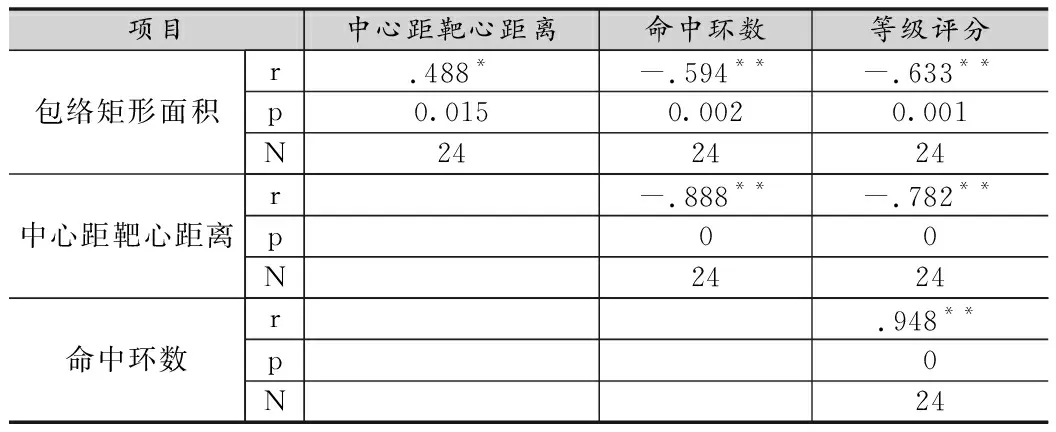
算法最小包络矩形输入 经过转换后的弹着点x轴、y轴序列,X=[x1,x2,…,xn]TY=[y1,y2,…,yn]T如果 n>3 计算出由X 和 Y构成的凸包,X=[x1,x2,…,xm],Y=[y1,y2,…,ym]。 构建变量nedges=m-1否则如果n>1 构建矩阵X=[x1,x2,…,xm,x1] and Y=[y1,y2,…,ym,y1] 构建变量nedges=n否则 构建变量nedges=n结束如果循环Switch nedges情况 0 do 输出 矩形四个顶点横坐标向量:rectx=[],纵坐标向量:recty=[],面积area=[]情况 1 do 输出rectx=[x1,x1,x1,x1,x1]recty=[y1,y1,y1,y1,y1]area=0 情况 2 do 输出rectx=[x1,x2,x2,x1,x1]recty=[y1,y2,y2,y1,y1]area=0 循环 i=1:m-1 do 计算凸多边形各边的角度edgeangles结束循环循环 i=1:m-1 do 构建最优面积betterarea=∞ 构建矩阵rot=[cosθ,-sinθ;sinθ,cosθ],θ=edgeangles(i) 计算矩阵 xyr=[X,Y]*rot 计算矩阵 xymin=min(xyr) and xymax=max(xyr) 计算面积area依据 (xymin[0]-xymax[0])* (xymin[1]-xymax[1]) 如果area

2.3 输出数据

通过已知包络矩形坐标顶点数据及角度数据进一步提取包络矩形中心点数值、长短轴数值和偏转角等信息。最小包络矩形算法优点是操作简单、时间复杂度低、易于实现。

3 实证及结果分析

3.1 研究方法

本研究主要采用对比法对现在使用的命中环数评价法和包络矩形评价法两种射击技术评价方法进行比较，证实包络矩形评价法的合理性和科学性。实验选取2名警校学员作为实验对象，他们均接受过系统的射击训练，2人日常射击技术水平相近，且近期无心理疾病且身体未有重大伤病。实验场地为室内实弹射击场，选用54式手枪进行实弹射击，射击点距胸靶7米距离[10-11]。要求射手在15秒内完成掏枪、出枪、瞄准及射击各项技术动作，并进行5发弹连续快速射击。2名射手各进行12轮手枪快速射击，共得到24张含有效弹着点的靶纸。结合转换后弹着点坐标点集，对命中环数评价法和包络矩形评价法分析结果进行相关性分析，对2名射手成绩进行差异性分析。

3.2 结果分析

将弹着点坐标数值代入包络矩形法中进行计算，结果表述为包络矩形面积、中心点和长短轴数据，同时使用命中点环数进行评价(表2)。胸环靶上最高环为10环，最低环为5环，计总环数，最高50环，最低0环。环数通常与等级评分挂钩，常见有两种评定方法，一是等级评定，45环及以上为优、40环至44环为良好、35环至39环为及格、34环及以下为不及格；二是分数评定，根据《2020年军队院校招生军事共同科目考核课目评分细则》，最高20分，最低0分，其中29环及以下记0分、48环及以上记20分。

表2 射击结果统计表

根据表2结果，依据命中点环数和等级评定，综合12轮射击成绩，可以认定射手B相对射手A成绩稳定，射手A表现出其射击状态起伏较大。但单从某一轮次如第3轮来看，射手A为45环，射手B为50环，但两者等级评价均为“优”，说明等级法并不能充分反映两人射击水平差异；如第1轮和第12轮，射手A环数均比射手B低3环，但第1轮射手A评分比射手B低2分，而第12轮射手A却比射手B只低1分，说明评分法在判断射手射击水平时具有一定的局限性。等级法和评分法均是以环数法为基础建立的判断射手射击水平的方法，两种方法并不能充分有效地对优秀射手射击水平和技术进行评价，不能直观反映出射手射击弹着点的散布情况。

对包络矩形面积、中心点距靶心距离、命中环数和等级评分等主要指标进行独立样本假设检验。表3结果表明，中心点距靶心距离、命中环数和等级评分上两名射手间存在显著差异，从均值和标准差数据上可以看出，射手A的弹着点散布中心相较于射手B距离靶心远，均值差异明显，表明中心点距靶心距离相对命中环数和等级评分更能明显区分两名射手的射击准确性差异。尽管包络矩形面积上表明射手A的弹着点分布密集度低于射手B，反映出射手A弹着点散布范围更大，射击稳定性和一致性低于射手B，但两者间没有统计学显著差异，这也与两名射手平时射击总体技能水平相近的现实情况一致，因此说明通过使用包络矩形评价方法评定射手的连续射击水平不仅能够有效区分射手的能力水平，也更贴近训练现实状况。

表3 射手差异性分析

进一步对指标结果进行Pearson相关性分析，表4结果表明所有指标之间均存在显著相关。其中中心点距靶心距离与命中环数存在具有极高显著性的高相关性(r=-0.888)，表明中心点距靶心距离可以有效表示命中环数结果，用于射击准确性评价。同时包络矩形面积指标与其他指标间均存在显著性中等程度相关，表明包络矩形面积指标可以作为一个辅助说明指标用于射击技术评价。

表4 相关性分析

结合包络矩形法对散布特征进行分析(表5)，射手A弹着点散布中心点、长短轴长上均大于射手B，表明射手B射击时弹着点更为集中，散布范围更小。需要注意的是两名射手的散布中心点在X轴的偏移量均小于Y轴，考虑到实际手枪射击采用并腿射击姿势，受枪械后坐力影响，连续射击时身体前后晃动和手腕的上下波动，这一结果有效地反映了射击技术的现实问题，对于射击技术改进具有指示性。同时包络矩形长短轴的使用，结合偏转角信息，能对解读射手射击技术诊断提供更多的细节信息，因此使用包络矩形法进行射击技术评价信息利用率高，评价更加全面。

表5 散布面积分布特征分析

4 结语

本文基于实战快速连续射击靶纸记录进行弹着点二维空间坐标提取，采用包络矩形算法进行弹着点分布特征分析和射击技能评价，得出如下结论。

(1)使用包络矩形算法进行射击技能评价操作简单、时间复杂度低、易于实现。得出的弹着点分布中心点距靶心距离可用于评价射击准确性，包络面积大小可用于评价射击的稳定性。

(2)使用包络矩形算法用于射击技能评价，信息利用率高，评价更加全面，通过分布信息提取，更能反映射击技术和能力特点，便于训练指导和技术改进。

随着现代军事作战和安全反恐形势变化，实战能力要求越发凸显，该方法用于不同场景下的射击技能实践应用将是下一步研究的重点。