火眼金睛找模型，水到渠成解图形

马正芳 何章鸣

◆摘  要：相似三角形是数学的核心内容，经常出现在压轴题，考查学生综合应用知识解决问题的能力，而这些问题的解决总是以一些基本模型为基础的.如果能掌握这些基本模型，并把它们从复杂的图形中挖掘出来，往往可将复杂问题简单化，问题的解决也就水到渠成.本文主要介绍相似三角形的四种基本模型。

◆关键词：相似三角形;数学模型;模型应用

相似三角形是数学的重要组成部分，是几何知识中的核心，容易出现在压轴题，并且经常与函数等知识相结合，图形相对复杂.但不管多么复杂的几何图形，都是由基本模型组成的.《义务教育数学课程标准（2011年版）》明确要求，学生能从较复杂的图形中分解出基本的图形，并能分析其中的基本元素及其关系，利用直观图形来进行思考.因此掌握相似三角形的基本模型，并能把它们从复杂的图形中挖掘出来，问题的解决也就水到渠成.本文由2020年长沙市中考第23题引出，主要介绍4种常见的基本模型，供同学们参考.

一、问题引入

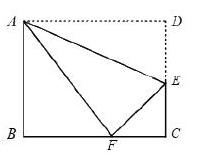
（2020 长沙）如图，在矩形ABCD中，E为DC边上一点，把△ADE沿AE翻折，使点D恰好落在BC边上的点F.（1）求证：△ABF[?]△FCE;（2）若AB=2[3]，AD=4，求EC的长;（3）若AE-DE=2EC，记∠BAF=α，∠FAE=β，求tanα+tanβ的值.

此题是对相似三角形中的三垂直模型的证明及应用，尤其是第（3）问，模型提供了解题的思路，有利于问题的解决.下面我们就相似三角形中的基本模型做一个归纳和总结.

二、模型归纳

模型一：“A”字型在图2-1-1中，已知DE∥BC，则△ADE∽△ABC，这就是最常见的“A”字型.变形1：如图2-1-2，已知∠1=∠B，则△AED∽△ABC，称为反A共角型.变形2：如图2-1-3，当点E与点C重合时，则△ACD∽△ABC，称为反A共角共边型，也称为子母型.变形3：如图2-1-4，当AC⊥BC，CD⊥AB时，则△ACD∽△CBD∽△ABC，称为双垂直模型.

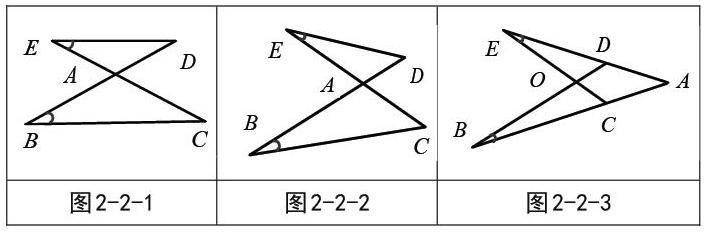
模型二：“X”字型在图2-2-1中，已知DE∥BC，则△ADE∽△ABC，这就是最常见的“X”字型.变形1：如图2-2-2，已知∠E=∠B，则△AED∽△ABC，称为反X型或斜X型.变形2：如图2-2-3，当ED和BC相交时，若∠E=∠B，则△AEC∽△ABC，△DOE∽△COB，有时也被称为燕尾型.

模型三：旋转型当“A”字型（图2-1-1）和“X”字型（图2-2-1）绕点A旋转时，就得到了下面的图2-3-1、图2-3-2和图2-3-3，称为旋转型.以图2-3-1为例，已知∠D=∠B，∠E=∠C，连接BD和CE（图2-3-4），则△ABD∽△ACE.图2-3-2和2-3-3中也有同样的结论.

模型四：一线三等角常见的模型还有一线三等角模型，经常与等腰三角形、函数图象等内容相结合，综合性较强.如图2-4-1所示，若∠B=∠C=∠EDF，则△BDE∽△CFD.特别地，当点D是BC的中点时，△BDE∽△DFE∽△CFD，并且ED平分∠BEF，FD平分∠EFC.有时也称为“K”字型.在特殊情形下，即相等的这三个角都是直角时，如图2-4-2所示，上述结论也成立，常常被称为三垂直模型或者“M”字型.

三、结论

在题目中快速找到模型，有利于发现问题的突破口，从而提高解题效率.这对绝大多数的几何问题也是适用的，基本模型是分析几何问题时观察的起点和目的，只有从复杂的图形中数量识别基本模型，才能正确得出与之对应的结论.值得注意的是当所给图形中不存在基本模型时，往往还需要添加辅助线进行构造.类似的基本模型，教材中还有很多，应予以重视，以更好地提高学生的综合分析和解题能力。

参考文献

[1]张小艳.运用基本图形巧证三角形相似[J].中学生数理化（初中版.中考版）， 2020，No.1208，29-31.

[2]張莲.挖掘基本图形，渗透转化和模型思想—浅谈一道旋转型相似的中考题[J]. 试题与研究， 2019（14）.

[3]鲁巧女.老歌新唱出新意，基本图形来演绎——中考专题复习《相似三角形之一线三等角图形》教学案例[J].青少年日记（教育教学研究），2019，No.152，218.

[4]付义娜.利用相似三角形基本图形解题[J].中学生数学，2018，No.590，17-18.

[5]向玫瑰.抓住基本图形突破相似判定[J].初中生学习指导，2018，No.1092.

[6]董德荣. 例谈相似三角形中的基本图形模型的巧妙应用[J].新高考， 2017， 000（011）：21-23.

作者简介

马正芳（1986.02—），女，山东泰安人，硕士，研究方向：数学教育，湖南省长沙市岳麓区南雅湘江中学。

何章鸣（1985.10—），男，广东乐昌人，博士，研究方向：数学教育、数据处理。

资助基金：湖南省学位与研究生教育教学改革研究课题（JG2017B008）;湖南省普通高等学校教学改革研究项目之“五位一体”本科全程导师制培养模式研究与实践（U2019003）;国防科大教育教学研究课题（U2017008;yjsy2017019）.