斜向地震作用下高轴压比RC方柱抗震性能试验*

宋 坤，王 伟

(1 燕山大学建筑工程与力学学院，秦皇岛 066004；2 绍兴文理学院土木工程学院，绍兴 312000)

0 引言

我国《建筑抗震设计规范》(GB 50011―2010)规定：“一般情况下，应至少在建筑结构的两个主轴方向分别计算地震作用”，但是建筑结构在地震中的响应监测结果显示，结构的层间侧移轨迹不一定与建筑主轴平行或垂直[1-3]，亦即，地震动可能以任意方向作用于结构构件[4]，从而导致其斜向受力。目前，已有学者针对斜向地震作用下钢筋混凝土(简称RC)长柱的抗震性能，围绕加载角度[5-8]、截面形式[9-10]、材料形式[11-14]等参数展开了试验研究，结果表明：矩形或方形截面柱，其斜向承载力与单向主轴(强轴)受力相比变差；异形截面柱在斜向与主轴向的抗震性能，因截面形式而有所差异。可见，斜向地震作用的影响不可忽视。但是，上述研究中，柱的轴压比主要集中于0～0.4的低轴压比情形。而随着建筑高度的增加和跨度的增大，钢筋混凝土框架结构或框架-剪力墙结构中，下部承重柱以及地下结构中的承重柱所承担的竖向荷载显著增加，常使其轴压比接近混规[15]中的上限值，形成高轴压比RC柱。因此，有必要开展斜向地震作用下高轴压比RC柱抗震性能的试验研究，以保证地震中结构的安全性。

本文制作了3个剪跨比为4的压弯型破坏RC方柱，控制轴压比为0.6，对其分别进行了0°，22.5°，45°加载角下的低周往复加载试验，在一定程度上解决了斜向地震作用下高轴压比弯曲破坏RC柱抗震性能试验缺乏问题。

1 试验概况

1.1 试件设计

共设计3个几何尺寸、配筋形式、材料属性皆相同，编号分别为D1，D2，D3的RC方柱试件。试验轴压比统一取0.6，根据荷载及材料强度设计值与标准值的换算关系，设计轴压比约为1.0，此值接近抗震等级较低的三、四级框架结构或框架-剪力墙结构的轴压比限值[15]。D1，D2，D3试件对应的加载角α分别为0°，22.5°，45°，意在研究高轴压比RC柱的抗震性能在斜向与主轴向的差异，及其随斜向地震动输入角度的变化规律。

方柱试件的几何尺寸详见图1。截面边长300mm，纵向柱高1 200mm，其中加载点至柱顶面108mm；柱下端与高500mm、宽400mm、长1 300mm的固定刚性支座相连；为保证22.5°和45°加载角的有效实施，在试件D2和D3的顶端设置边长为440mm的正方形混凝土加载端，在柱试件底端与刚性支座交界面处，方形支座截面尺寸局部增大至500mm×500mm，且在方形截面四角增设沿支座高度方向的角部纵筋及箍筋(图1)。

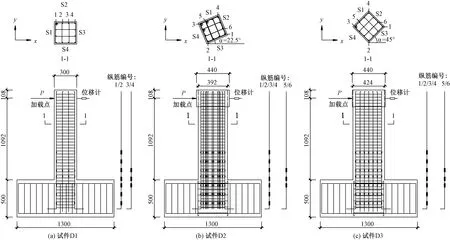
图1 柱截面尺寸及配筋

为保证所研究试件发生弯曲型破坏，设计其剪跨比为4，且配筋形式(图1)满足“强剪弱弯”原则。其中，纵筋为1212钢筋，沿柱横截面均匀分布，配筋率为1.0%；箍筋为φ6@40mm的四肢箍形式，配箍率为2.1%；钢筋的实测强度、弹性模量见表1；保护层厚度为15mm，混凝土轴心抗压强度实测平均值为43MPa。

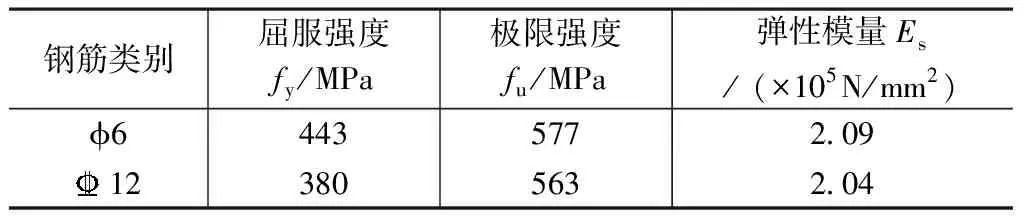
钢筋材料力学性能 表1

1.2 加载装置及加载原则

试验的加载装置如图2所示，由控制轴力的竖向作动器和控制水平荷载的水平作动器组成。试验过程中采用力-位移混合控制加载方法实施加载，加载全程保证缓慢、匀速。首先，对柱顶施加竖向荷载至预定轴力值。此后，以屈服荷载的20%为增量幅度逐级施加水平荷载，每一级循环1次，此处屈服荷载取为逆向数值积分算法[16]估算的峰值荷载的80%；当荷载加至屈服荷载后，改为位移控制加载，以100%的屈服位移为增量幅度逐级实施加载，每一级循环3次，直至试件无法继续承担水平或竖向荷载时，结束试验。加载过程中，始终实时调节竖向作动器以保证恒定的轴压比。

图2 加载装置

1.3 测点布置

试验通过布设传感装置以获取外力、位移及钢筋应变信息。水平荷载及竖向荷载由作动器上的力传感器采集；试件的水平位移由“与加载点位于同一水平面上”的位移计采集(图1)；纵筋应变由其上布置的应变片采集，各试件纵筋测点布置如图1所示，其编号规则为DX-Y-Z，其中DX表示试件编号，Y表示钢筋编号，Z表示应变片距离底座顶面的距离。

2 试验结果及分析

2.1 试验结果

(1)破坏过程

3个试件在出现首条裂缝后，其破坏过程皆表现出随位移增大，裂缝沿纵向增多，沿横向延伸、增宽的规律。各试件在开裂点、屈服点、破坏点(荷载下降到峰值荷载的85%)的表征如表2所述，最终破坏形态如图3所示。为便于试验结果的描述，以S1，S2，S3，S4标注柱外侧面(图1)。

试验结果 表3

图3 试件破坏形态

(2)滞回曲线

各试件的滞回曲线如图4所示。由图可知：滞回环的捏拢现象随着加载角α的增大而加重。

图4 滞回曲线

(3)骨架曲线及割线刚度

骨架曲线是滞回曲线上各加载级中第一次循环的反向加载点连线，各试件的骨架曲线如图5所示；曲线上的三个关键点，即屈服点(此处按照能量法[17]确定)、峰值荷载点、破坏点的推、拉向水平荷载的平均值及位移平均值见表3。由图5(图中竖向实线表示±8mm位移点，近似为表3中各试件的屈服点位移)以及表3可知，屈服荷载Py、峰值荷载Pp、破坏荷载Pu与加载角α呈负相关关系，α=45°时的Py，Pp，Pu约为α=0°时的91%，84%，84%；各关键点对应的位移Δy，Δp，Δu与α的关系为先升后降，在本试验中，α=22.5°时各关键点处位移最大，即变形能力最好。

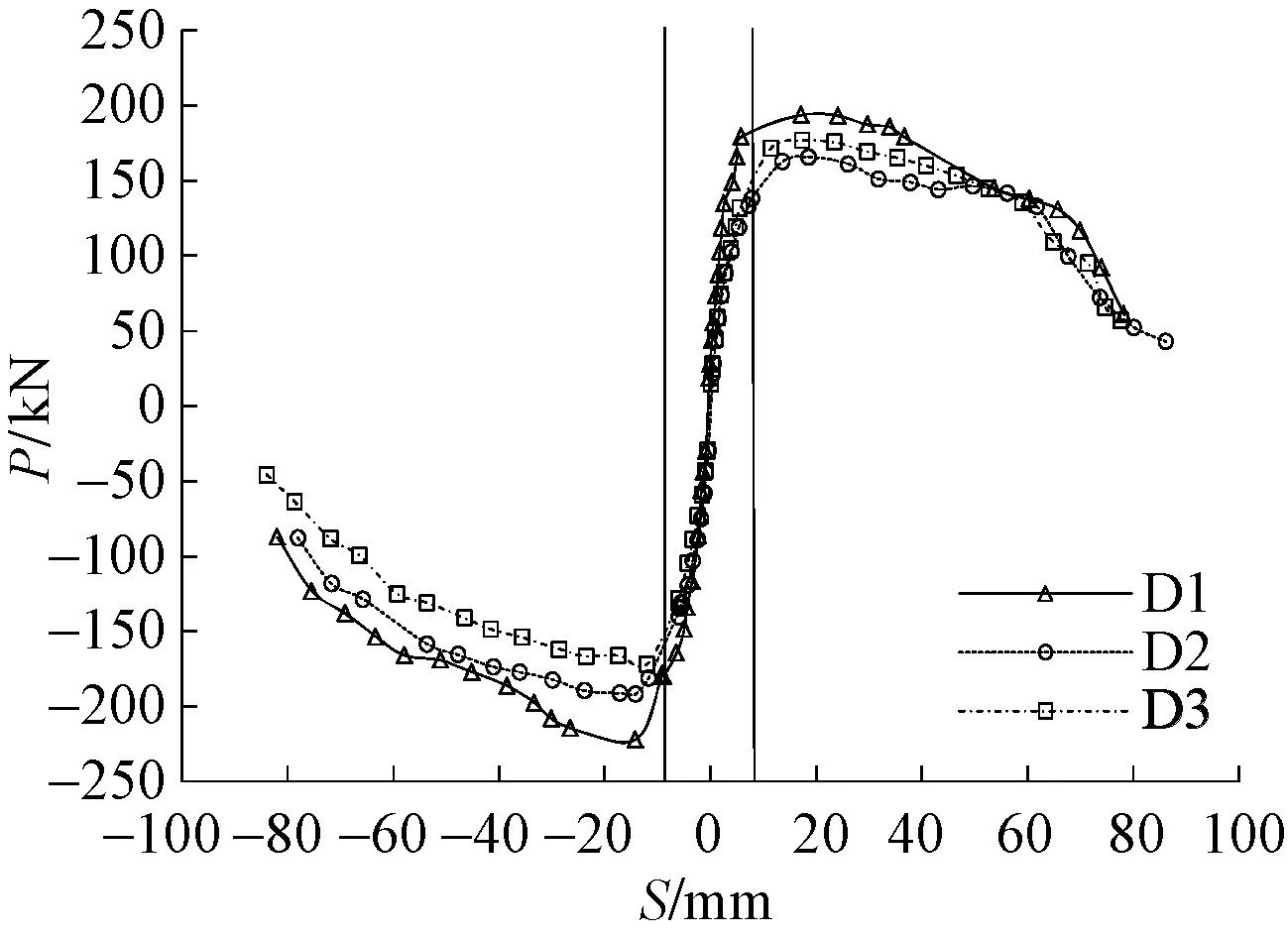
图5 骨架曲线

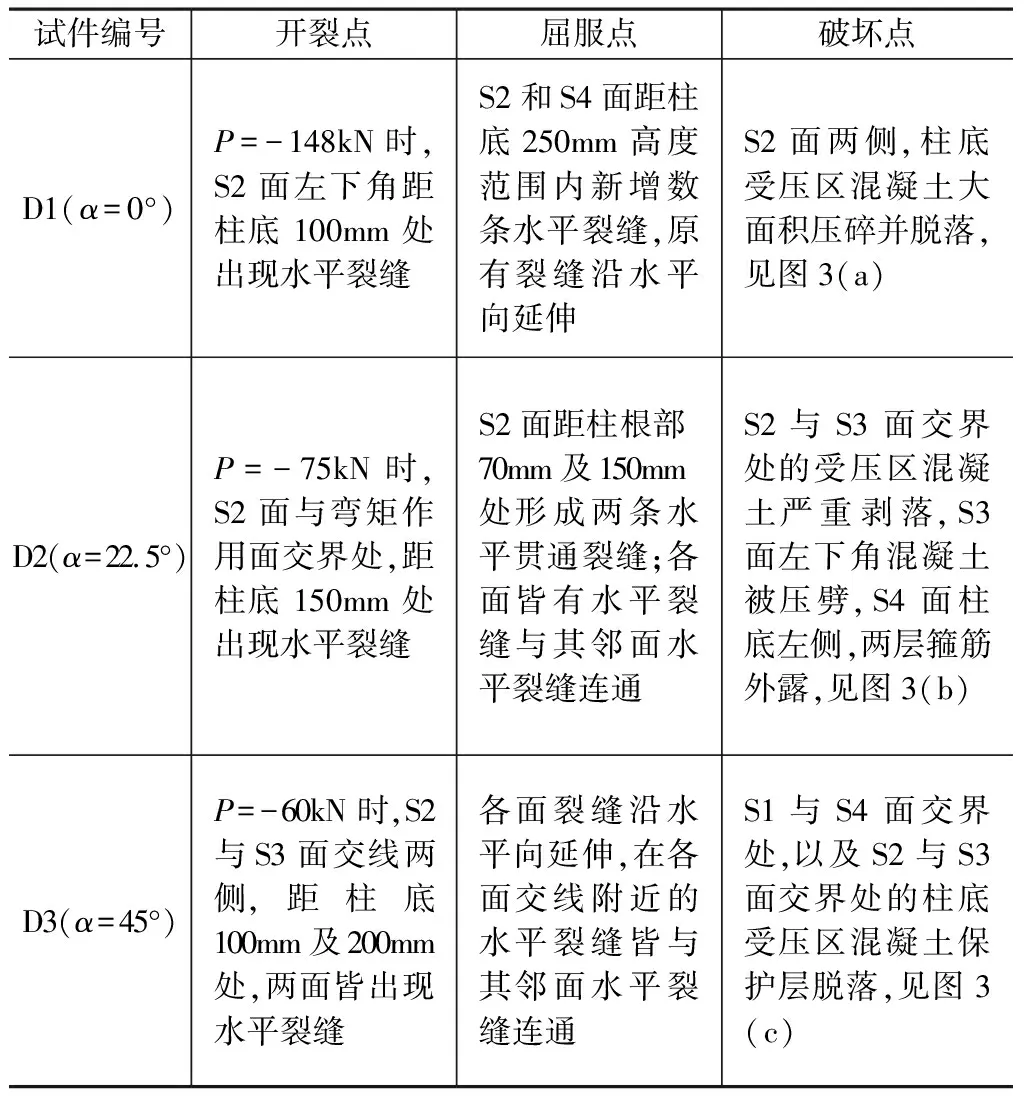
试件破坏过程 表2

由图6割线刚度-位移(Ki-S)曲线可知(图中竖向实线表示8mm位移点)，加载角度对割线刚度的影响并不显著。

图6 割线刚度-位移曲线

(4)耗能性能

本文采用等效黏滞阻尼系数he=SC/2πSΔ来衡量试件在单个循环中的耗能性能[18]，其中，SC为各加载级的第一次循环形成的荷载-位移曲线所围成的曲面面积；SΔ为推、拉两个方向“坐标原点、反向加载点、反向加载时的位移轴坐标点所围成的”三角形面积。he越大，构件耗能能力越强，即抗震性能越好。各试件的能量耗能系数-位移he-S曲线如图7所示。由图可知，α=45°时试件耗能能力最好，α=22.5°时试件耗能能力最差。

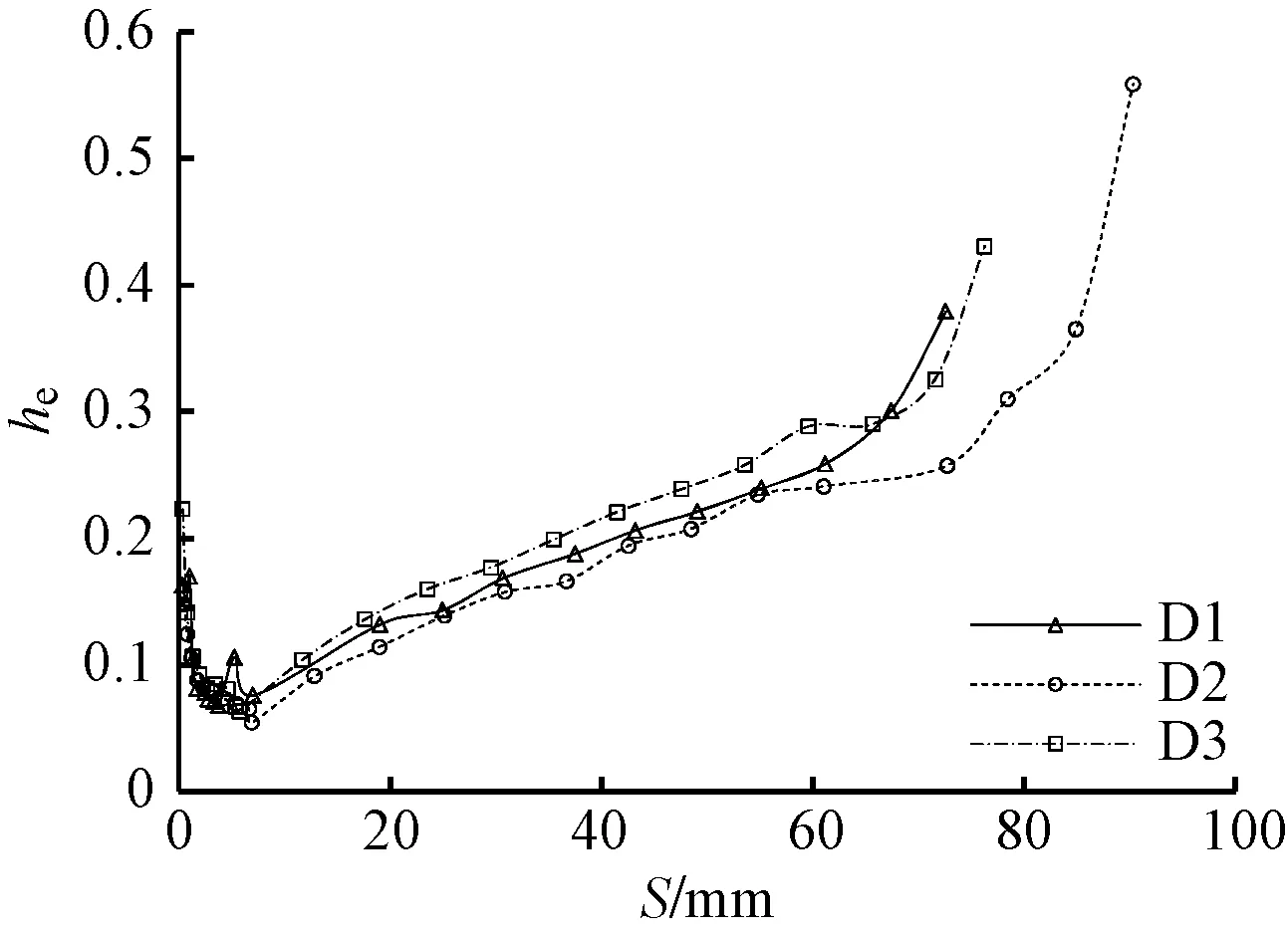
图7 耗能系数-位移曲线

(5)延性

本文采用位移延性系数μi=Δu,i/Δy,i和转角延性系数θi=Δu,i/h衡量试件的延性，其中h为加载点至柱底的距离；Δy,i为屈服点位移，Δu,i为破坏点位移；下标i指代加载角度(定义x，y轴方向分别为0°和90°)。各试件的μi，θi见表4。依据3个加载角下的试验数据及试件截面的对称性拟合出的μi及θi与加载角α的关系曲线见图8，其中α∈[0°,90°]。

延性系数 表4

由表4及图8知：各试件的μi均大于3[19]，θi均大于0.035；斜向受力下试件的延性优于沿主轴受力下的延性，22.5°加载时延性最好。

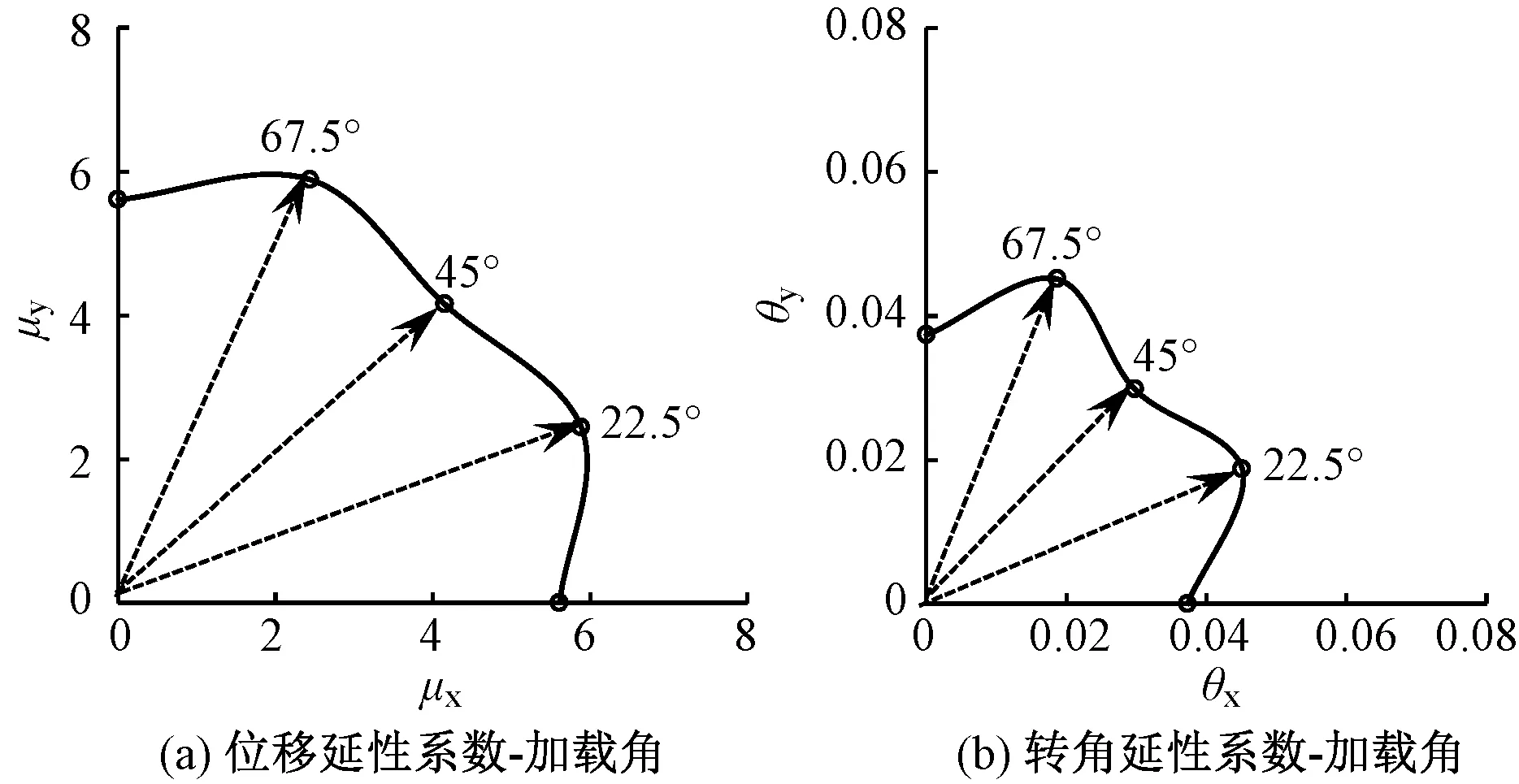
图8 延性系数-加载角

(6)钢筋应变

各柱内具有代表性的纵筋测点的应变-位移曲线见图9，图中水平虚线的纵坐标值为1 863με，即纵筋的屈服应变值，各试件钢筋应变特征如下：

图9 钢筋应变

1)试件D1：Δy≈7.3mm时，D1-1-40首先达到1 863με(屈服值)，此时骨架曲线具有明显的拐点；Δu≈40.8mm时，D1-2-40也已达到屈服值。

2)试件D2：Δy≈8.4mm时，D2-1-40首先达到屈服值；Δp≈16.5mm时，除邻近中性轴的两根纵筋(编号：2，4)上的测点外，其余纵筋上的测点都已达到过屈服值，如D2-6-40。

3)试件D3：Δy≈7.8mm时，D3-1-40首先达到屈服值；随着位移增大，当Δp≈14.7mm时，与其相邻钢筋上的测点达到屈服值，如D3-6-80。

由图9及上述特征可知：距中性轴较远的混凝土受拉区域处的纵筋首先进入屈服，此时往往伴随着刚度的退化(图5)，随后，距中性轴较近的混凝土受拉区域纵筋按照距中性轴由远及近的顺序依次达到屈服。各试件在屈服点、峰值荷载点和破坏点处，达到屈服值且可有效工作的纵筋数量因加载角度而变；屈服点处，随加载角α的增大，试件内达到屈服的钢筋数量减少；屈服点后，随着水平荷载的增加，斜向加载试件沿加载方向的角部钢筋部分出现断裂并退出工作，故已达到屈服且可有效工作的钢筋数量仍表现出随加载角度的增加而减少的趋势；因此，承载力随加载角α的增大呈下降趋势。

2.2 试验结果分析

(1)滞回曲线、耗能能力及延性

由图4知，试件屈服后，由于纵筋粘结滑移导致滞回曲线出现捏拢现象，发生粘结滑移的纵筋数量表现出斜向加载高于主轴向加载，且与加载角度α(α∈[0°,45°])呈先增后减的关系，本文试验中，D2试件(α=22.5°)滞回曲线的捏拢最明显，故耗能能力最差(图7)，但较多的钢筋发生粘结滑移却导致较高的延性(表4)。

(2)屈服点、峰值荷载点、破坏点

由表3及图9分析结果可知，3个关键点处的荷载皆随加载角度的增大而下降，其原因如下：在屈服点、峰值荷载点及破坏点时刻，受拉区混凝土早已开裂；此时，对于同一数值的水平力P，在距柱顶同一高度h的正截面Sh上，不同的加载角α产生不同的受压面积区Ah、拉/压区合力Fh、合拉力点至(与轴向外力作用下重合的)中轴的距离dh(图10)；由弯矩平衡可得Ph=Fhdh。依据纵筋上的应变测点数据并结合表3及表5知，随着α的增大，dh增大，Fhdh减小。进而推知，Ah上Fh减小的速率快于dh增大的速率。

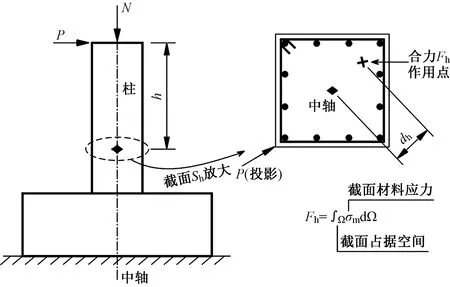
图10 柱段隔离体静力平衡示意

(3)割线刚度

随着水平位移的增大，试件中的裂缝逐渐开展，纵筋逐渐进入屈服状态，故试件的割线刚度出现退化；Δ≈8mm时，刚度突然变小(图5，6)，此点与各柱内首次出现纵筋应变达到屈服值的分析结果相符。

(4)正截面承载力

试件在固定轴压比情形下，理论上可依据截面上首次出现混凝土极限压应变而估算相应的正截面极限弯矩(计算值)。本文采用文献[16]提出的逆向数值积分算法估算全部试件的正截面极限弯矩计算值，并将其与试验值进行对比，结果见表5。由表5可知，计算值与试验值误差范围为6.3%～8.9%，由此可见，逆向算法可用来预估斜向受力RC方柱的正截面承载力。

计算结果对比 表5

3 结论

(1)斜向受力导致高轴压比RC柱承载能力下降，滞回环捏拢现象加剧，刚度无显著变化，但变形能力增强。

(2)各项抗震性能指标随地震动输入角度的变化规律表征为：正截面承载力与加载角α(α∈[0°,45°])呈负相关关系，能量耗散系数随加载角的增大先降后升，延性系数则先增后减，以22.5°加载试件的耗能能力最差，但变形能力最好。

(3)采用逆向数值积分算法估算的斜向受力RC柱的峰值荷载，估算值与试验值较为接近。

(4)本文仅对方形RC柱进行了研究，后续可针对工程中更为普遍的矩形截面钢筋混凝土柱，研究其在高轴压比情形下，抗震性能与正截面边长比、加载角的关系。