方波工况下PMSM 单电流调节器控制策略的研究

王 震，周明磊，王琛琛

（北京交通大学电气工程学院，北京 100044）

永磁同步电机PMSM（permanent magnet synchronous motor）具有高功率密度、高效率以及高功率因数等一系列优点，因而被越来越多地应用于轨道交通领域。轨道交通领域中逆变器的开关频率通常较低，电机在高速区通常运行在方波工况。方波工况下电机电压幅值达到最大值，完全失去调节能力，仅有电压矢量角可供调节，而传统基于双电流环的控制策略不再适用，因此方波工况下控制策略的研究是轨道交通用永磁同步电机重点研究内容之一。

永磁同步电机方波工况下的控制策略可以分为电流指令计算和电压指令计算两个部分。其中电流指令计算环节的目的是为了得到合适的电流指令，常用的方法主要包括公式法[1]、查表法[2]、梯度下降法[3]以及负直轴电流补偿法[4]等，其中负直轴电流补偿法原理简单且鲁棒性较好，是目前应用较多的一类方法。电压指令计算环节的目的是根据得到的d、q 轴电流指令，经过一定的控制算法对d、q 轴电压进行调节，最终实现对电机输出转矩的控制，其常用的方法大致可以分为3 类：①通过电机数学方程计算得到电压指令[5]，鲁棒性较差，而且由于没有电流环，无法实现电流的准确跟踪控制；②通过基于双电流环的控制策略调节得到电压指令[6-7]，但由于方波工况下电压幅值达到最大值，无法调节，需要对调节器输出的电压指令重新进行复杂的修正，以匹配方波电压输出，计算复杂且动态性能一般；③通过基于单电流环的控制策略调节得到电压指令[8-14]，具有良好的电流跟踪性能和动态性能，同时有效避免了双电流调节器耦合而产生的饱和冲突问题，是目前应用最多的一类方法。文献[8]通过单个电流调节器调节d 轴电压并建立电机的q 轴电压和电流的线性函数，修正电机q 轴电压的指令值，进而得到电压指令；文献[9-10]在其基础上用查表法替代线性函数的方法来确定q 轴电压进而得到电压指令；文献[11]通过电压幅值与单电流调节器输出的d 轴电压得到q 轴电压进而得到电压指令，充分利用了直流侧电压；文献[12-13]提出在牵引工况利用d 轴电流调节器，在制动工况利用q 轴电流调节器来调节电压矢量角，并结合电压幅值得到了电压指令；文献[14]提出无论是牵引还是制动工况均可以通过单q 轴电流调节器调节电压矢量角，并结合电压幅值得到了电压指令。

上述文献仅对基于单电流环控制策略的某一种方法进行了分析，并未对方波下不同控制策略之间的联系与区别进行梳理总结。本文针对方波下只有电压矢量角一个变量可供调节的现状，通过分析不同变量之间的关系，可得方波工况下共有6 种基于单电流环的控制策略，而目前应用于方波工况下的单电流环控制策略属于这6 种方法之一。通过建立小信号模型，对这6 种控制策略的稳态性能和动态性能进行对比分析。最后通过仿真和实验验证了理论分析的正确性。

1 方波下永磁电机的转矩控制方法

当PMSM 运行在高速区时，定子电阻上的压降可以忽略不计，在两相同步旋转坐标系下的稳态电压和转矩方程为

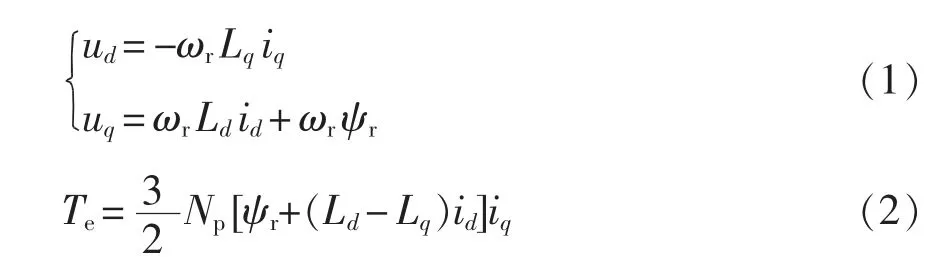
式中：ud和uq为定子电压的直轴和交轴分量；id和iq为定子电流的直轴和交轴分量；Ld和Lq为直轴和交轴电感；ωr为电机同步电角速度；ψr为电机转子磁链；Te为电机的电磁转矩；Np为电机的极对数。

轨道交通用永磁电机的控制目标为转矩，在方波工况下电压幅值达到最大值，即usmax=2Udc/π，Udc为直流侧电压，此时仅有电压矢量角一个变量可供调节。为了证明可以通过调节电压矢量角来控制转矩，需要证明转矩和电压矢量角始终满足一一对应关系。定义电压矢量角θ 为电压矢量与d 轴电压的夹角，方波工况下的d、q 轴电压分别表示为

结合式（1）～式（3），转矩方程可以通过θ 表示为

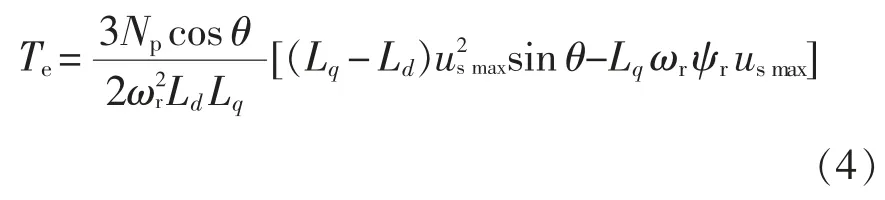
基于电机参数，电机转矩Te与电压矢量角θ的关系曲线如图1 所示。θ 的可调范围在（0，π）内，在此范围内θ 和转矩始终满足单调关系，即一一对应关系，因此可以通过调节θ 来控制转矩。

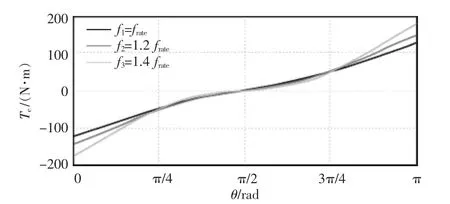
图1 转矩与电压矢量角的关系Fig.1 Relationship between torque and voltage vector angle

除了直接调节θ 之外，还可以通过调节d、q 轴电压间接调节θ。但由于θ 与d、q 轴电压并非线性关系，因此为了证明可以通过调节d、q 轴电压来控制转矩，需要证明转矩和d、q 轴电压同样满足一一对应关系。d、q 轴电压用电压幅值可以表示为

结合式（2）和式（5），转矩方程可以表示为

基于电机参数，电机转矩与d、q 轴电压的关系曲线如图2 所示。由图2（a）可知，d 轴电压ud始终和转矩呈单调关系，即一一对应关系，因此可以通过调节ud来控制转矩；图2（b）中虚线代表制动工况，实线代表牵引工况。当牵引和制动工况下转矩的绝对值相同时，uq虽然相同，但ud方向相反，故可以通过控制ud的正负来控制输出转矩的正负，即控制电机运行在牵引或制动工况。无论是牵引工况还是制动工况，uq与转矩始终满足单调关系，因此可以通过调节uq来控制转矩。

图2 转矩与d、q 轴电压的关系Fig.2 Relationship between torque and d/q-axis voltage

由上述分析可知，通过调节θ 和ud、uq可以控制转矩。同时为了进一步提高转矩的稳态精度以及动态响应速度，需要加入电流闭环控制实现这几个变量的自动调节。

2 基于单电流环的方波控制策略

为了避免双电流调节器饱和的问题并获得较好的动态性能，可以选择单电流调节器对θ 和ud、uq这3 个变量闭环调节。电流调节器输入可以为id和iq，输出可以为θ 和ud、uq。为了进一步了解这6 种单电流调节器，需要对调节器输入变量和输出变量的关系进行分析。

结合式（1）和式（3），可得id、iq和θ 的导函数关系为

牵引工况和制动工况对应的θ 的范围分别为：（π/2，π）和（0，π/2）。由式（8）可知，id和θ 在制动工况呈正相关，在牵引工况呈负相关；iq和θ 始终呈正相关。

结合式（1）和式（5），可得id、iq和ud、uq的导函数关系为

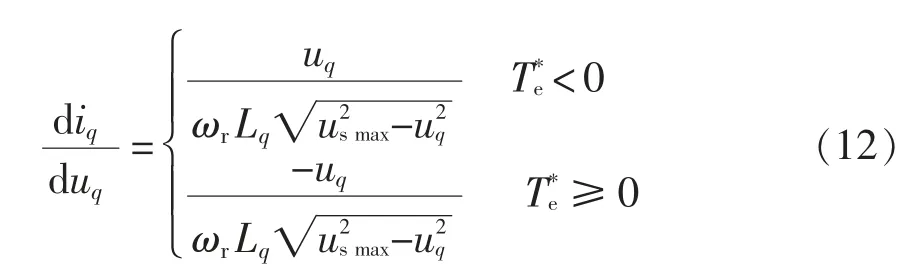
由式（9）～式（12）可知，id和ud在制动工况呈负相关，在牵引工况呈正相关；iq和ud始终呈负相关；id和uq轴电压始终呈正相关；vq和uq在制动工况呈正相关，在牵引工况呈负相关。

通过分析上述不同变量之间的联系，方波工况下共有6 种单电流环的控制策略，分别为：单d 轴电流调节器调节电压矢量角SDCR-VVA（single daxis current regulator-variable voltage angle）、单d 轴电流调节器调节d 轴电压SDCR-VDV（single d-axis current regulator-variable d-axis voltage）、单d 轴电流调节器调节q 轴电压SDCR-VQV（single d-axis current regulator-variable q-axis voltage）、单q 轴电流调节器调节电压矢量角SQCR-VVA（single q-axis current regulator-variable voltage angle）、单q 轴电流调节器调节d 轴电压SQCR-VDV（single q-axis current regulator-variable d-axis voltage）、单q 轴电流调节器调节q 轴电压SQCR-VQV（single q-axis current regulator-variable q-axis voltage）。电流指令计算环节框图如图3 所示，本文采用负直轴电流补偿法计算电流指令。电压指令计算环节框图，即方波工况下的6 种单电流环控制策略框图如图4 所示。

图3 电流指令计算框图Fig.3 Block diagram of current command calculation

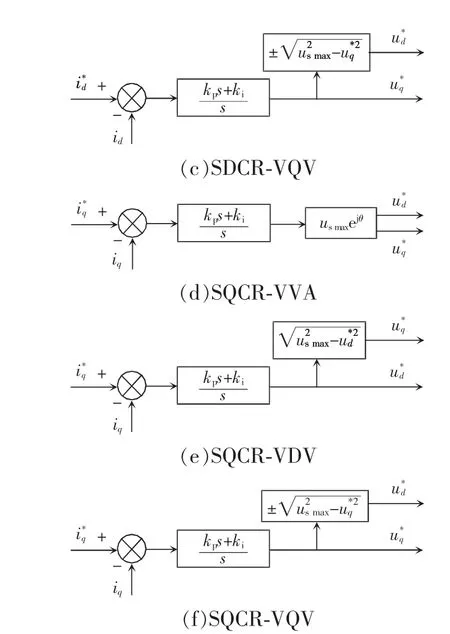
图4 6 种单电流环控制策略框图Fig.4 Block diagram of six single-current loop control strategies

3 稳定性及动态性能分析

建立小信号模型，对这6 种单电流环控制策略方法的稳态性能和动态性能进行分析比较。限于篇幅，仅以SQCR-VDV 的控制策略为例进行分析。

3.1 控制策略的小信号建模

SQCR-VDV 控制策略的小信号模型框图如图5 所示。

图5 SQCR-VDV 小信号模型框图Fig.5 Block diagram of small-signal model of SQCR-VDV

小信号模型对应的传递函数G（s）为

式中：Δiq和分别为q 轴电流的实际值和指令值的变化量；a0、a1、a2、a3、b0、b1、b2为系数，其表达式分别为

小信号框图中，参数ku为q 轴电压变化量Δuq和d 轴电压变化量Δud的比值，即

通过劳斯判据对其稳定性进行分析。满足劳斯判据的参数关系有2 组，表示为

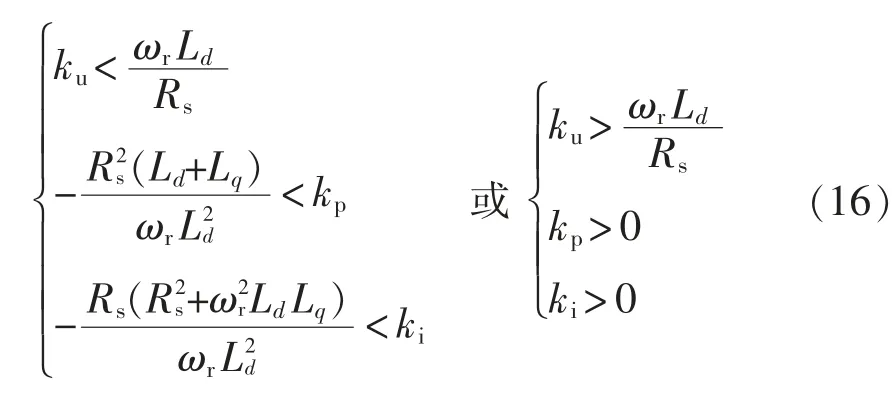
这两组解所对应的ku的范围以及调节器参数范围均不同，说明在这两组解对应的工况中需要分别选取合适的调节器参数才能实现系统的稳定。

3.2 稳定性分析

基于电机参数，选取合适的调节器参数对其稳态性能进行测试。测试工况为：轻载±0.1Trate、中载±0.5Trate、重载±0.8Trate，电机频率范围为50～65 Hz，极点分布情况如图6 所示。由图可知，在任何工况下系统极点均在左半平面，说明该方法具有全局稳定性。

图6 SQCR-VDV 不同工况极点分布Fig.6 Distribution of poles under different working conditions of SQCR-VDV

3.3 动态性能分析

为了提升系统的动态响应速度，需要选取合适的调节器参数。测试工况设置为电机转矩为15 N•m，电机频率为65 Hz，不同PI 参数对系统极点的影响如图7 所示，图中，参数kp的变化范围为0.1～0.5，箭头方向代表kp增大方向。由图7 可见，kp相比于参数ki对系统极点的影响较小，可以忽略，因此主要分析ki对系统极点的影响。在牵引工况，随着ki的增大，共轭极点向虚轴靠近，实轴极点远离虚轴；在制动工况，随着ki的增大，共轭极点向虚轴靠近，实轴极点远离虚轴。无论是牵引工况还是制动工况，随着ki增大，系统都将出现超调和振荡现象。

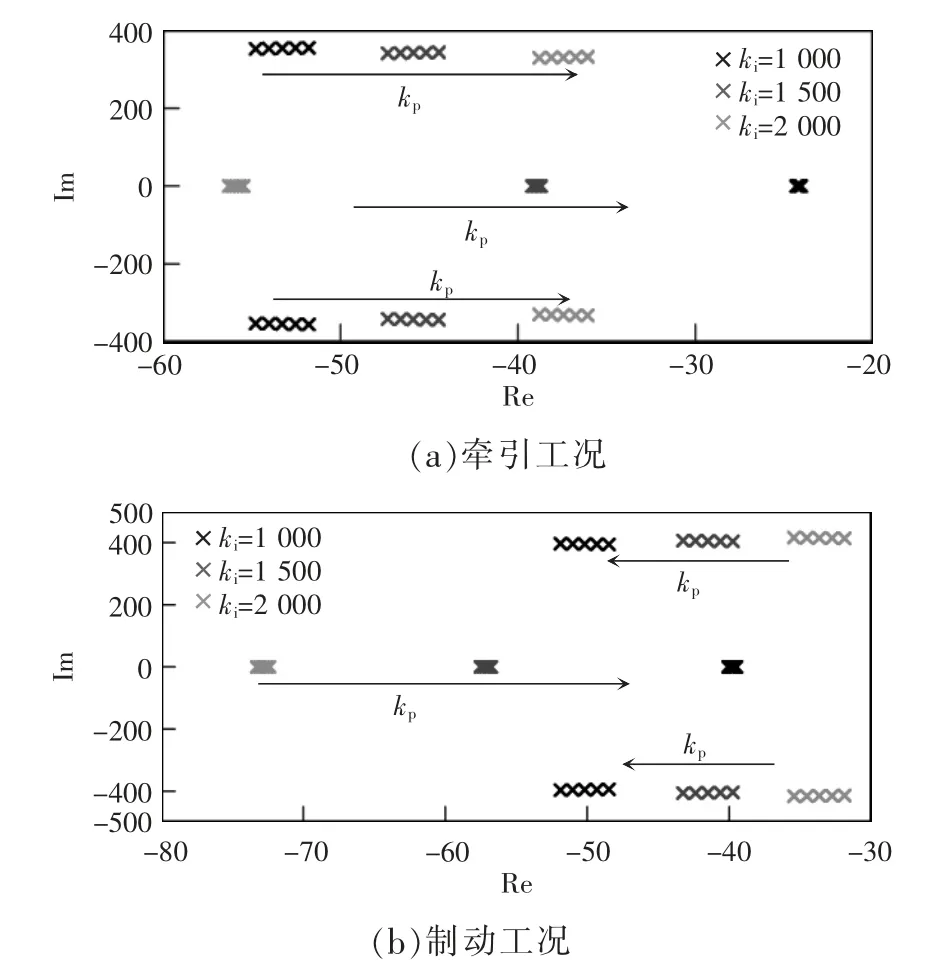
图7 PI 参数对系统极点分布的影响Fig.7 Influences of PI parameters on the distribution of system poles

固定kp为0.5，选取不同的ki对系统做阶跃响应测试，结果如图8 所示。随着ki的增大，动态响应速度有所提升，但当ki选取过大时，系统逐渐出现超调和振荡，因此ki不能选取过大，可选取kp=0.5、ki=2 000。

图8 不同PI 参数下的阶跃响应测试结果（kp=0.5）Fig.8 Step response test results under different PI parameters（kp=0.5）

3.4 6 种控制策略的比较

通过对比劳斯判据结果与文献[15]推导的有限转速系统电机有效弱磁区域，从是否需要切换调节器参数的角度比较这6 种方法，结果示意如图9 所示。图中，阴影部分对应的曲线ABDC 为有效弱磁区域，圆上实线与虚线分别为劳斯判据两组解对应的ku的范围，可见，SQCR-VDV 和SQCR-VVA 这2种方法仅使用1 组调节器参数即可实现全弱磁区域的稳定运行，而其他4 种方法在使用1 组调节器参数的条件下均无法实现全弱磁区域的稳定运行。

图9 6 种控制策略的比较结果Fig.9 Comparison results among six control strategies

4 仿真与实验结果

本文的仿真和实验采用的电机参数如表1 所示。

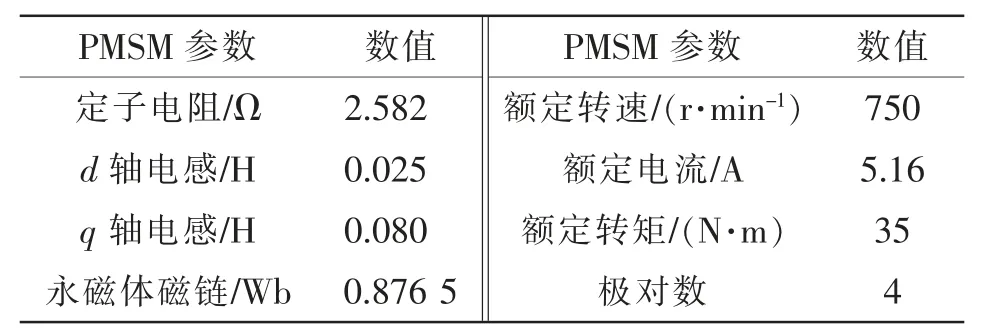
表1 仿真与实验所用电机参数Tab.1 Motor parameters in simulation and experiment

4.1 仿真结果

仿真工况设置为：电机频率65 Hz，转矩在7 s时由25 N•m 切换到-25 N•m，且在整个运行过程中每种控制策略仅采用1 组调节器参数。6 种控制策略稳态性能比较的仿真结果如图10 所示，图中Flgwk为弱磁标志位，其值为100 时为弱磁控制。由图可见，SQCR-VVA 和SQCR-VDV 这2 种控制策略在整个切换过程中电流和转矩均能稳定跟随，即可以在不改变调节器方向的情况下实现方波控制；SDCR-VQV 在制动轻载工况会存在电流和转矩不能稳定跟随的现象，而其他3 种方法在进入制动工况后会存在电流和转矩不能稳定跟随的现象，即这4 种方法在仅使用1 组调节器参数的条件下均存在不稳定区域。仿真结果与图9 所示的理论分析结果一致，验证了理论分析的准确性。

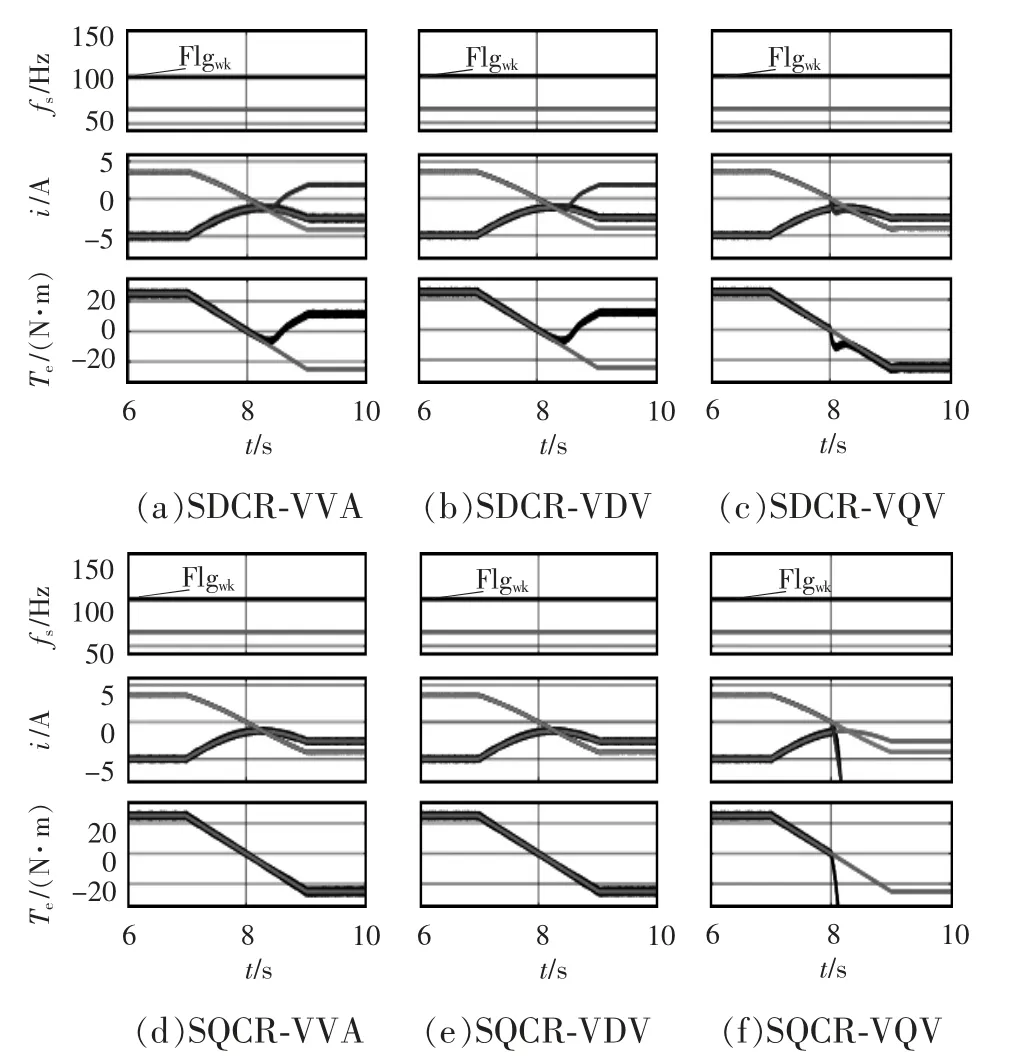
图10 稳态性能比较的仿真结果Fig.10 Simulation results of steady-state performance comparison

仿真工况设置为：电机频率为65 Hz，在4 s 时转矩由10 N•m 阶跃至15N•m。6 种控制策略动态性能比较的仿真结果如图11 所示。由图可见，相较于其他5 种方法，无论是牵引工况还是制动工况，SQCR-VDV 都具有较优的动态响应速度，动态响应时间大约为30 ms。

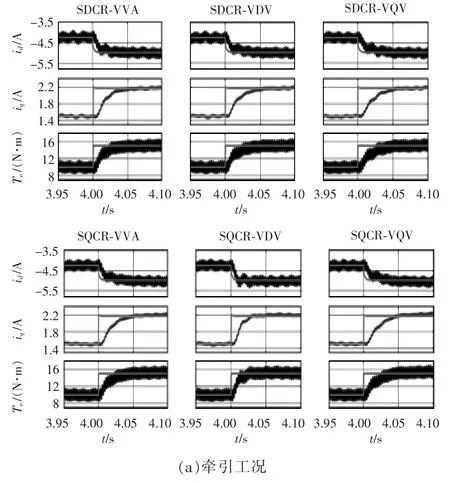
图11 动态性能比较的仿真结果Fig.11 Simulation results of dynamic performance comparison

4.2 实验结果

为了验证上述理论分析和仿真结果的准确性，搭建如图12 所示的永磁同步电机对拖实验平台，实验电机参数见表1。

图12 实验平台Fig.12 Experimental platform

实验工况与仿真工况一致，6 种控制策略稳态性能比较的实验结果如图13 所示。由实验结果可知，SQCR-VVA 和SQCR-VDV 这2 种控制策略可以在不改变调节器方向的情况下实现方波控制，SDCR-VQV 在制动轻载工况会存在电流和转矩不能稳定跟随的现象，而其他3 种方法在进入制动工况后会存在电流和转矩不能稳定跟随的现象，即这4 种控制策略在仅使用1 组调节器参数的条件下均存在不稳定区域。实验结果与仿真结果基本一致，进一步证明了理论分析的准确性。

图13 稳态性能比较的实验结果Fig.13 Experiment results of steady-state performance comparison

图14 为SQCR-VDV 控制策略下电机频率为65 Hz，转矩为15 N•m 工况时电机稳定运行的结果。实验工况与仿真工况一致，6 种控制策略动态性能比较的实验结果如图15 所示，实验结果与仿真结果基本一致，相较于其他5 种方法，SQCRVDV 控制策略具有较优的动态性能。

图14 SQCR-VDV 的稳态波形Fig.14 Steady-state waveforms of SQCR-VDV

图15 动态性能比较的实验结果Fig.15 Experimental results of dynamic performance comparison

5 结语

本文通过推导转矩和电流与电压矢量角和d、q 轴电压的关系，可知方波工况下共有6 种单电流环的控制策略。通过建立小信号模型对这6 种控制策略的稳态性能比较可知，SQCR-VVA 和SQCRVDV 这两种控制策略仅使用1 组调节器参数便能实现全弱磁区域的稳定控制；对这6 种控制策略的动态性能比较可知，SQCR-VDV 这种方法具有最优的动态性能。最后通过仿真和实验验证了上述分析的准确性。