用线性规划助力数学解题教学

曹如祥

(福建省上杭县第一中学 364200)

“要以‘学生立场’贯穿教育教学过程，基于核心素养的教学要把握知识本质，创设教学情境.”《普通高中数学课程标准》修订组组长史宁中如此说道.在高中教学中应如何破解一些数学题，满足新时代人才需求呢？解决数学问题的能力构建了数学与外部世界的桥梁，是数学应用的重要方面，是应用数学解决实际问题的基本手段，是推动数学发展的外部驱动力.通过培养学生解决数学问题的能力，使学生能够掌握解决数学问题的过程，积累用数学的语言表达实际问题的经验，提升应用能力和创新意识.线性规划是高中数学的重要知识点，是解答相关数学习题的重要工具，为使学生灵活运用线性规划知识，解答相关的数学习题，促进其解题能力的不断提升，应注重对学生讲解经典例题.运用线性规划知识解答数学习题时，应根据已知条件明确可行域，并画出对应的可行域，尤其应明确其是否包含边界，而后通过转化要求解的问题，借助几何知识找到破题思路.

一、应用线性规划进行解答向量习题教学

分析解答该题需要运用向量运算，找到已知条件和要求解问题之间的关系，而后运用线性规划知识解答.

二、应用线性规划进行解答不等式习题教学

分析解答该题需要明确x2+y2≤m表示的含义以及m取得最大值的情境，运用线性规划以及几何知识进行分析.

三、应用线性规划进行解答概率习题教学

分析该题具有一定难度，解题的关键在于能够对给出的方程进行转化，而后运用线性规划知识，求出对应图形的面积，便可求出满足题意的概率.

四、应用线性规划进行解答函数习题教学

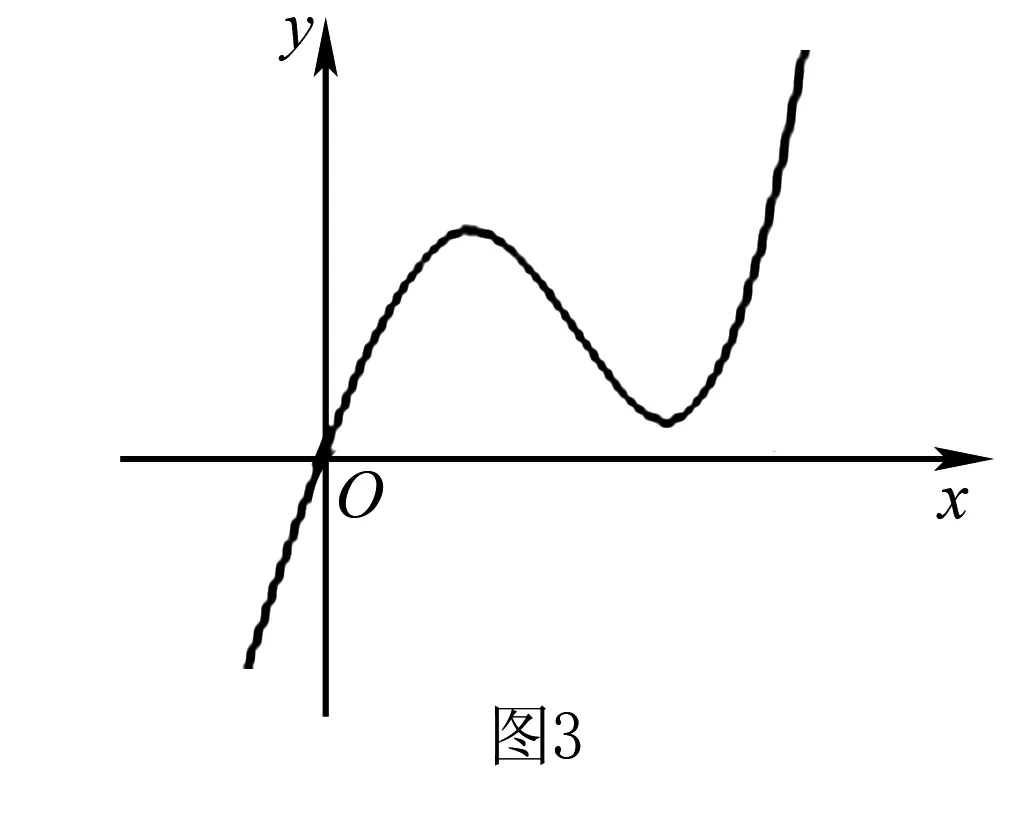
分析解答该题需要根据已知条件找到a，b的可行域，而后求点(-2，-2)与可行域中点的斜率取值范围(不包含边界)即可.

数学解题是通过对实际问题的简化和抽象后，用数学原理建立模型，用数学方法解决问题，再回到实际情境中解释、验证所得结果的数学活动过程.本文通过解题模式化找到处理问题的方法.在实际教学中为提高学生解答数学习题的灵活性，应注重为学生深入剖析相关题型，使其做好听课总结，把握不同题型的解题思路，并在课下多进行训练，积累相关的解题经验与技巧，在解题中能够融会贯通，举一反三.