蒙特卡洛方法模拟二维伊辛模型的相变分析

詹明浩 张威威 梁炳清 余宝明 蒋蓝毅

（1.北部湾大学，广西 钦州 535011；2.常州大学，江苏 常州 213000）

0 前言

在研究系统处于平衡态时的热力学性质时，通常通过对配分函数求导得到系统的热力学函数[1]。在物质发生相变时，相变点的某些热力学量会发生突变或者出现无穷尖峰，必须通过建立体现系统核心特性的模型，得到其在相变点的宏观特性，才能从单一的配分函数表达式中同时描述相和相的转变。从20世纪30年代中叶开始，统计物理学对统计模型的大量研究已经形成了一个专门的领域，诞生了许多模型，在解释铁磁性的问题上，伊辛模型体现了它的优势[2]。伊辛模型尽管很成熟、非常经典，但是现在也需要不断地对其进行验证。而对于蒙特卡洛方法，不断将它与新的科学技术结合，使之获得新的生命力并得到发展，尝试性地取得一些微小的进步是非常具有意义的。综上所述，用蒙特卡洛方法（MC）模拟二维伊辛（lsing）模型的相变过程就显得尤为重要。

1 蒙特卡洛方法与伊辛模型

1.1 伊辛模型

考虑1个一维的铁磁体，定义这个自旋粒子，用（↑↓）分别表示自旋的方向。将该粒子排列在规则的晶格上。20世纪20年代楞次（Wilhelm Lenz）教授就是由此创立了伊辛模型，一维伊辛模型的示意图如图1所示。

图1 一维伊辛模型示意图

图1中每一个黑点代表一个自旋，它们之间存在最近邻的相互作用。一维伊辛模型给出的结果如下：一维的伊辛模型只有一个相，不存在相变。该结果正是1925年楞次教授的博士生伊辛的成果，因此该模型也被称楞次 -伊辛模型。

1944年该理论出现了一个重要进展，美国科学家昂萨格教授解出了2D伊辛模型的解析。

图2（a）是8×8的1个二维伊辛模型晶格，黑点代表自旋，图2（b）是以中心自旋n为例的相互作用的示意图，n1，2，3，4是不同位置的最近邻自旋，其相互作用关系用{i，j}来表示。在这里，笔者给出最初昂萨格的解[3]，即Tc=2.269。

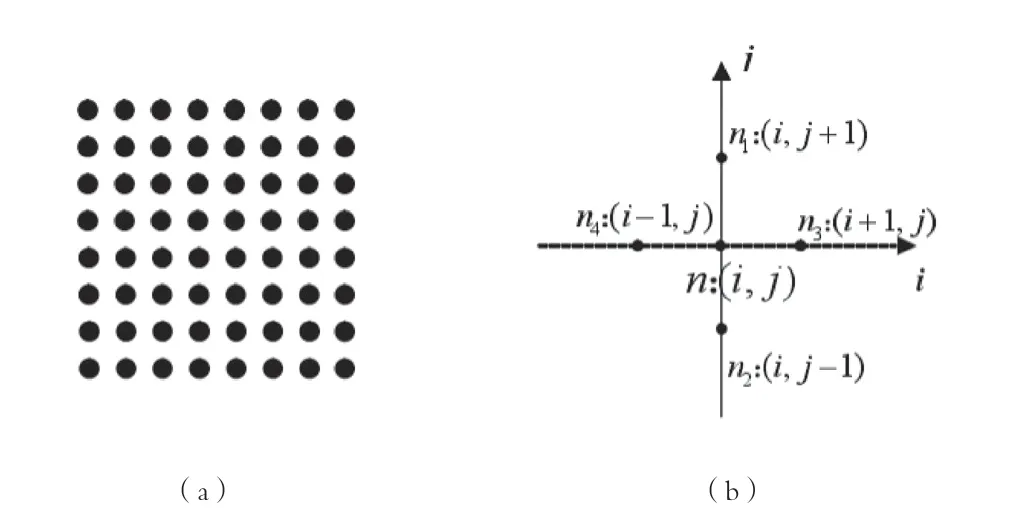
图2 二维伊辛模型示意图

1.2 蒙特卡洛方法的基本思想

伊辛模型系统各格点上的自旋取值抽样采用了Metroplis 方法[4]。这对于伊辛模型来说虽然不是最高效的采样方法，但却是最易于实现的方法。该文采用MATLAB软件在20×20的晶格中进行模拟。蒙卡方法的基本思想如下：对于某一问题的随机模拟，通过问题的解来设定参数，根据现实情况来建模。以多次随机模拟来求得问题的概率。设随机变量的数学期望是E（ξ），对ξ进行N次模拟得到各个ξ值，可得到其算术平均值ξN如公式（1）所示。

式中：ξ为ξN的计算结果。

当N→∞时，。

首先，产生随机数r1，r2，且它们范围是0～1的数。

其次，将r1和r2对应于直角坐标系上的x、y值，如果r2≤e-r1，那么就可多设一个未知数v来表示观察的次数，符合统计规则，v加1，N也加1；如果r2＞e-r1，那么不符合统计规则，则v加0，N加1。

再次，多次重复上述步骤。

最后，得出结果。

2 二维伊辛模型的蒙特卡洛模拟

比热容、能量与温度T的关系如公式（2）所示。

图3为2D伊辛模型的比热容Cv与平均能量E随温度的变化，上部分图的热容量Cv与下部分图的平均能量E相对应。比热可以作为判断相变的标准，且其判断结果比较精确，它在相变时作为热力学量会出现尖峰，E表示单个格点的平均能量，当温度趋于0时，所有格点同向。

图3 比热容Cv与平均能量E随温度T的变化

当温度趋于无穷时，格点方向随机，某格点四周平均有2个同向和2个方向，E=0。通过模拟得到图4。图4中模拟的比热在临界温度时会突然增大，需要吸收极大的能量，这也很符合相变的特点，在这之后比热逐渐下降。可以看出在温度低于相变临界温度的情况下，热容量随温度的升高而增大；在高于相变临界温度时，随温度的升高而减小。当温度为2.273 K时，热容图像由升到降出现相变，这与相变临界温度理论值2.269 K吻合，该结果对二维伊辛模型的进一步研究具有深远的意义，同时也是下一步研究的基础。

3 磁场及耦合强度对二维伊辛模型相变点临界温度的影响

3.1 结果与讨论

3.1.1 磁场对伊辛模型的影响

如图5所示，在不同磁场作用下相变点存在以下变化，见表1。

表1 2D伊辛模型在不同磁场B作用下系统的相变临界点

在之前的基础上，通过计算机模拟了耦合强度J=1，对磁场B=0、B=0.3、B=0.5、B=0.7以及B=0.9进行计算，用磁感应强度B来表示磁场强度，磁场强度H的单位为A/m，换算关系为B=4π×10-7N/A2·H，得到图像如图5所示的关系图，上部分图的热容量Cv与下部分图的平均能量E相对应。

从图5可以看出，磁场对伊辛模型有作用，使系统相变温度出现了延迟，磁场绝对值越大，相变临界温度就越高。当存在外磁场时，相变临界点随着外磁场的增大向高温方向移动，这是由于外磁场使自旋趋于有序排列，而热运动使自旋趋于无序排列；随着外场的增大，磁场的作用逐渐增强，无序区间向高温方向压缩，而有序区间则向高温方向扩大，导致临界温度增高；因此，当外磁场足够强时，系统几乎在整个温度空间内处于有序状态且会出现相变临界的现象。

3.1.2 耦合强度对伊辛模型的影响

不同耦合强度下系统热容量和平均能量的关系如图4所示。

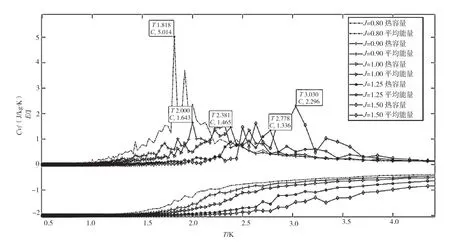
图4 在不同耦合强度J作用下系统比热容Cv与平均能量E随温度的变化

由图5可知，在不同耦合强度作用下相变点存在以下变化，见表2。

图5 不同磁场B作用下系统比热容Cv与平均能量E随温度T的变化

表2 2D伊辛模型在不同耦合强度作用下系统的相变临界点

这里讨论了耦合强度对伊辛模型的影响，取外磁场B=0，分别取耦合强度J=0.8、J=0.9、J=1、J=1.25以及J=1.5进行计算，计算结果如图5所示，上部分图的热容量Cv与下部分图的平均能量E相对应。

从图5可以看出，在不同耦合强度下，系统的能量总是呈上升的趋势，随着耦合强度的增大，能量曲线向右平移，相变临界值增加。得出结果为2.381，与预期相变点2.269存在误差，之所以存在误差，可能是由以下2个原因导致的：1）实验本身误差。2）相邻局域的温度不同，相互之间有耦合作用。

耦合强度在一定波动范围内对二维伊辛模型的相变存在影响，耦合强度越大，相变点临界温度也越高。如果耦合强度变化过大，将会使模拟失败，这违反了基本自旋相互作用的假设。

3.2 模拟结论

在模拟过程中还发现了如下问题：当程序接近相变临界点时，Metroplis方法会收敛得很慢，单个自旋的翻转统计会导致如果系统准备进入完全自旋向上或自旋向下时，突然接受了某个粒子的翻转，那么又会从头进行一轮新的统计，这就会导致在亚稳态停留的时间过长，甚至出现无法收敛到稳态而一直停留在亚稳态的情况。希望在以后条件允许的情况下可以对算法的这个问题进行改进。

4 结语

在用MC模拟二维伊辛模型的相变的问题上，前人有非常丰富的经验，该文通过查阅文献资料，重现了MC模拟二维伊辛模型的相变过程，并对该过程进行模拟、探索、对比与分析，丰富了该理论的模拟过程，从而使该理论得到发展。

同时，该文还重新模拟这个古老又经典的模型，是对真理的不断验证，还可以为其他科技工作者给予参考。

进一步研究耦合强度与温度关系中磁化率和磁化强度的规律对该模型具有重要意义；运用平均场理论计算合理的磁场梯度，在适当的马尔可夫链长和步数下进行模拟；对采样算法进行改进，优化相变临界点的收敛速度。