Two-point model analysis of SOL plasma in EAST

Jie HUANG(黄杰),Yasuhiro SUZUKI(鈴木康浩),2,Kunpei NOJIRI(野尻訓平),Naoko ASHIKAWA (芦川直子),2 and EAST Team

1 National Institute for Fusion Science, National Institutes of Natural Sciences, Oroshi-cho, 322-6, Toki 509-5292, Japan

2 The Graduate University for Advanced Studies, SOKENDAI, Oroshi-cho, 322-6, Toki 509-5292, Japan

3 Plasma Research Center, University of Tsukuba, 1-1-1 Tennodai, Tsukuba 305-8577, Japan

4 Institute of Plasma Physics, Chinese Academy of Sciences, Hefei 230031, People’s Republic of China

Abstract A two-point model is used to investigate the characteristics of scrape-off layer (SOL) plasma with the field line tracing method in the experimental advanced superconducting tokamak.The profiles of plasma density, temperature and particle flux on the divertor target calculated by the model are in reasonable agreement with experimental observation.Moreover, the profiles of plasma parameters on the divertor target strongly depend on the SOL magnetic topology or the equilibrium configuration from the modeling.

Keywords: scrape-off layer, two-point model, field line tracing, tokamak

1.Introduction

In magnetic fusion devices the main plasma is confined with nested closed magnetic flux surface.The region radially outboard of the last closed (magnetic)flux surface(LCFS)or separatrix is called as the scrape-off layer (SOL) where flux surfaces are all open and magnetic field line will connect directly to the wall elements [1].In the tokamak operation there are generally two categories SOL, the limiter and divertor.In a divertor configuration the main or confined plasma and the SOL are separated by the magnetic separatrix where the magnetic flux surface passes through the X-point generated by a divertor coil, resulting in principally different magnetic topology.As the divertor SOL can move the solid surface (the divertor target) where the intense plasma-surface interactions occur away from the confined plasma, future tokamaks such as the International Thermonuclear Experimental Reactor (ITER) are relying on divertor to play a crucial part in particle control and power exhaust [2].

The plasma parameters in the SOL are really important for characterizing both the plasma behavior in confined volume and the plasma-wall interaction.Normally sophisticated two-dimensional or three-dimensional codes like SOLPS [3] or EMC3-EIRENE [4, 5] including time dependence are used to analyze the conditions of plasma boundary in front of the solid wall for magnetic fusion devices.Nevertheless,the reduced analytical models can also be used for rough estimate of the characteristics of plasma boundary, which can give a qualitative physical understanding of transport process in SOL aiming at interpretation and understanding of experiments and save the computation time.One simplest and useful analytical model is the twopoint model[1],which is based upon the assumption that the heat and particle transport are purely parallel to the individual flux tubes or the magnetic field lines, as mainly relevant to a divertor SOL.The two points are referred to the upstream and target,hence the model is also called as the zero-dimensional divertor model.

Three modes of divertor operation, the sheath-limited,high-recycling and detached regime, have been classified experimentally [6].In the sheath-limited regime, the plasma pressure and temperature are constant along each flux tube and the input heat from the main plasma is little dissipated.As the simple SOL,the physics of sheath-limited divertor can be described by the basic two-point model well.In the highrecycling regime,the plasma pressure remains nearly constant while the plasma temperature significantly drops parallel to the flux tube from the SOL to the divertor target due to the finite heat conductivity, as most of plasma energy is dissipated by collision with recycling neutrals or by radiation before incident on the divertor target.While a steady-state recycle refueling in front of the divertor target balances the plasma pressure.In the detached regime, substantial pressure loss exits near the separatrix and both the plasma density and temperature drop parallel to the flux tube.For the latter two modes of divertor operation,the basic two-point model can be extended with the correction factors for the effects of including power loss and pressure loss processes.

In this paper, a two-point model is used to analyze the characteristics of divertor SOL plasma in experimental advanced superconducting tokamak (EAST), which is fast and light for computing, and the influence of equilibrium configuration on the divertor plasma is investigated with the modeling and experimental observation.Section 2 presents the experimental setup.Section 3 presents the physical model and numerical method.Compared with the experimental observation,section 4 presents the modeling results of plasma parameters profiles on the divertor target, and the profiles dependence of the equilibrium configuration.A summary is given in section 5.R=1.85 m, minor radiusa=0.45 m, toroidal magnetic fieldBT～3.5 T,plasma currentIp～1 MA,triangularityδ=−0.4 0.7, and elongationκup to 1.9 [7].

To study the influence of equilibrium configuration on the characteristics of divertor plasma, the experiment was performed with the USN configuration in EAST.The upper divertor is equipped with water-cooled W/Cu plasma-facing components[8]and the plasma properties on the divertor can be measured by the Langmuir probe installed on the plate.Three discharges (shots #84816–84818) with different equilibrium configurations were performed in EAST.The main plasma parameters for the three discharges are almost same with toroidal magnetic fieldBT～2.4 T,

2.Experimental setup

EAST, as a fully superconducting tokamak with ITER-like configuration which has a flexible selection of upper single null(USN),lower single null,or double null poloidal divertor configurations, is aimed at investigating physical issues of long-pulse high-performance advanced tokamak operation.The design parameters of EAST are major radius plasma currentIp～1 MA,line-averaged plasma density～1.8×1019m−3,and lower hybrid wave heating with a power of ～1 MW in L-mode.A rough structure of EAST vacuum vessel and the USN equilibrium configuration with separatrices are shown in figure 1.The striking point on the upper outer (UO) divertor targets was shifted to the divertor corner from #84816 to #84818 with different equilibrium configurations.

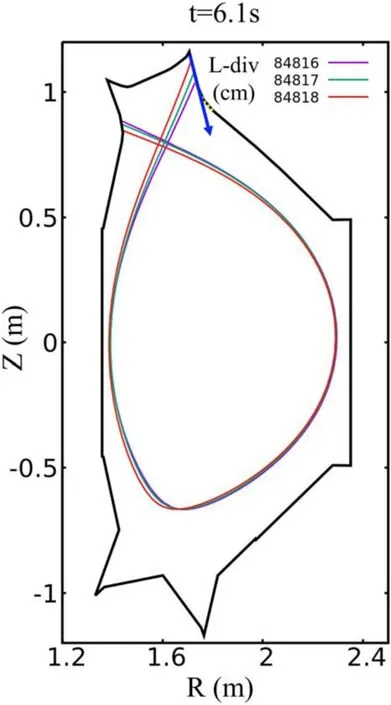
Figure 1.A rough structure of EAST vacuum vessel and separatrices for EAST shots #84816–84818 at =t 6.1 s.The yellow dots represent the Langmuir probes on the UO divertor plate.L-div in centimeter represents the distance of the point on the UO divertor to the divertor corner.

3.Physical model and numerical methods

In this paper we consider the corrections two-point model as discussed in [1], which can be extended to the analysis of high-recycling or detached divertor plasma.The model is based on the following three principal physical processes:the heat conduction, pressure balance and power balance.

(1) Heat conduction equation:

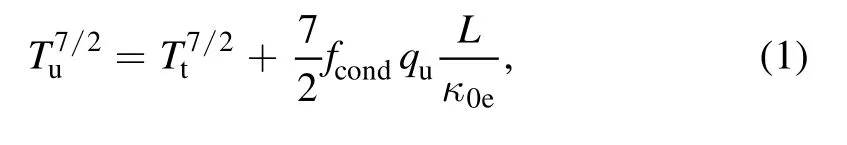
whereTuandTtare the plasma temperature of upstream and target point, respectively.HereTe=Ti=Tis assumed,whereTeandTiare the electron and ion temperature,respectively.Lis the flux tube length or the field line connection length between upstream and target.quis the heat flux density entering into the upstream point.κ0eis electron parallel conductivity coefficient, which is set as constant withκ0e≈2000in the calculation.Here the ion heat conductivity is neglected as comparatively small and assume ions and electrons are thermally coupled.The conduction factorfcondis introduced for the parallel heat convection effects on heat transport,which will reduce the temperature gradient.

(2) Pressure balance equation:

wherenuandntare the plasma densities of upstream and target point, respectively.fmomis the momentum loss factor as the plasma flow toward the target point may lose momentum due to viscous forces,frictional collisions with neutrals and volume recombination.For the sheath-limited or the high-recycling regimes, the pressure keeps almost constant, givingfmom=1.

(3) Power balance equation:

whereqtis the heat flux density entering into the target point,γ is the sheath heat transmission coefficientγ≈7.cstis the ion sound speed,is the power loss factor for the volumetric power losses including radiation and charge exchange loss.

In equations(1)–(3),L,γ andκ0eare specified constants.Settingnu,qu,fcond,fmom,fpoweras specified control parameters, i.e.the independent variables, the remaining three unknowns,nt,Tt,Tucan be solved by the classical method with the assumption ofTu72≫Tt72[1]:

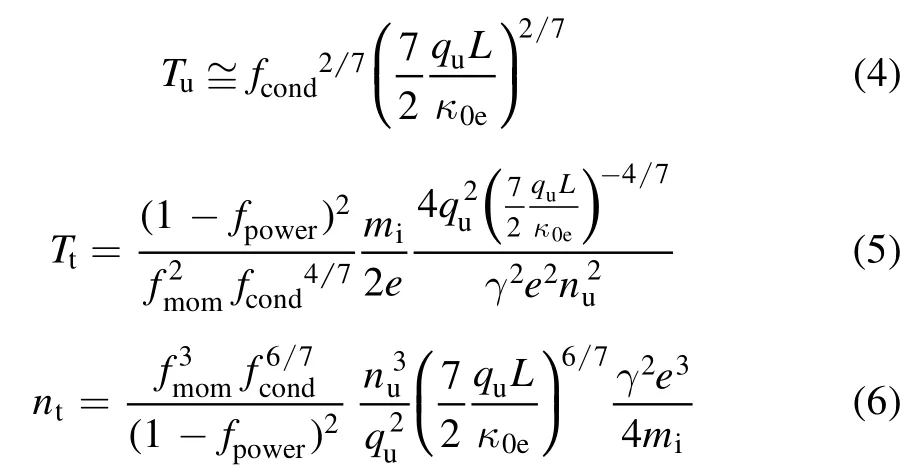
and the particle flux density:

Here the units:L(m),q(W m−2),T(eV),n(m−3)andeis the electronic charge,miis the ion mass.

In this paper we directly solve the equations (1)–(3) by numerical method without any approximation.Combining equations (2) and (3) to obtain:

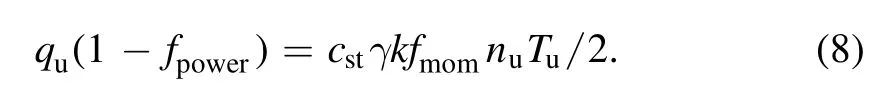
SettingTuasx1andTtasx2,the problem turns to solve the following two-dimensional nonlinear equations:

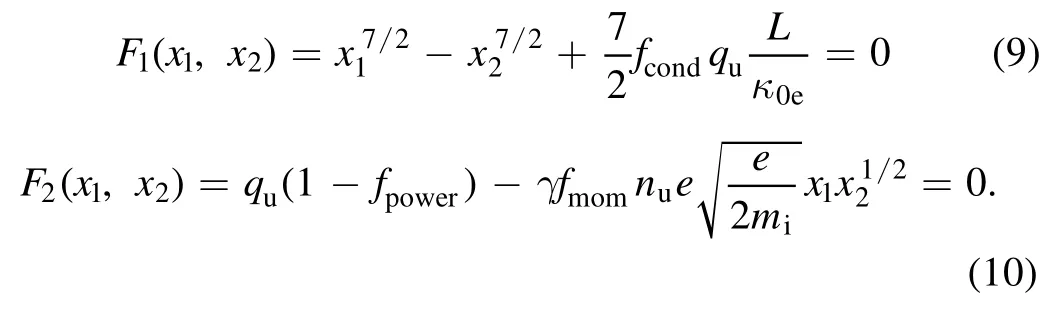
Equations (9) and (10) can be easily solved by Newton–Raphson method[9]with the initial guess for the roots which can be given by equations(4)and(5).FollowingntandΓtcan be easily deduced whenTuandTtare already known.

To obtain precise connection length,the field line tracing method is used forLcalculation.In the cylindrical coordinate(φRZ, , ), the field line equation can be expressed as:

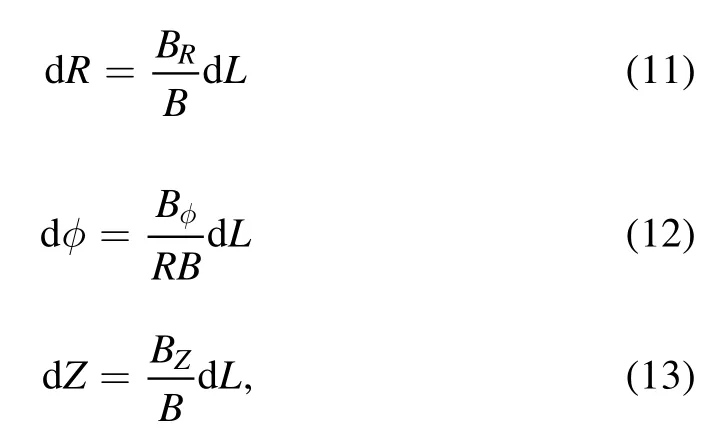
whereBR,Bφ,BZare the magnetic field components in the cylindrical coordinate.

With the magnetic field information given by EFIT[10],the field line trajectory can be traced by integrating the first order equations(11)–(13).Here the fourth order Runge–Kutta method is used for theLintegration.

To extend the 0-dimensional two-point model to the main SOL region, a series of the upstream points as shown in figure 2 are set on the midplane from separatrix to the wall and the reciprocal target points are searched by the field line tracing method.Given the appropriate density and power decay length and other control parameters, the profiles of plasma density, temperature and particle flux density on the divertor target can be calculated by the model.

The control parameters for EAST shots #84816–84818 are set as follows: the conduction factor is set asfcond=1 neglecting the influence of convection as comparatively small in the parallel conduction dominating heat transport.The momentum loss factor is set asfmom=1according to [11]since the temperature of target points is larger than 10 eV from experimental observation.Or the SOL plasma is characterized by high-recycling regime.To balance the modeling result with experiment, the power loss factor for the two points of upstream on separatrix/LCFS and striking/target point on divertor target is set asfpower,LCFS=0.5.Here we assume the loss of power is purely dissipated by impurity radiation given by [12]:

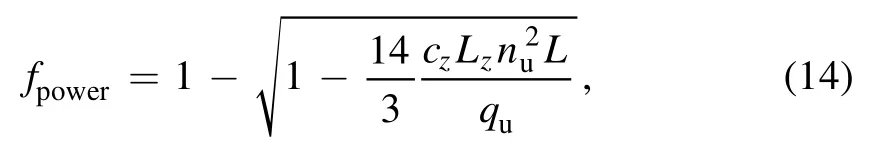
whereczis the impurity concentration,Lzis the radiation

coefficient.With the value offpower,LCFS,the value ofcz Lzcan be deduced and the profile of power loss factor for the series of the two points can be obtained by equation (14).

The plasma density at LCFS is set asnLCFS=/3,whereis the line-averaged plasma density.Assuming the plasma density of upstream points located at the midplanenu(r) is exponential, thennu(r) can be estimated by [1]:

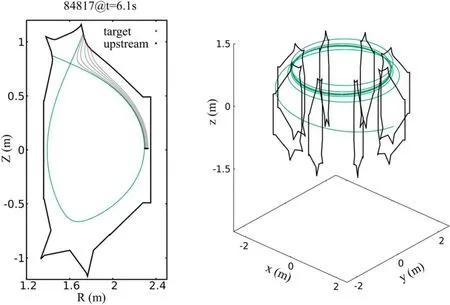
Figure 2.A series of the two points with the target located at the Langmuir probes for the analysis of SOL plasma in EAST(left)and 3D view of the magnetic field line between upstream point located at separatrix and reciprocal target point (right) for EAST shot #84817.Here the upstream points are set on the midplane from separatrix to the wall along R direction.

Figure 3.The connection length L between the series of upstream points and reciprocal target points for EAST shots #84816–84818.Here one dot represents a pair of two points in the modeling.

The heat flux density entering the upstream point located at LCFS is estimated asqLCFS=50 MW m−2.Similarly,assuming the heat flux density of upstream points located at the midplanequ(r)is exponential,thenqu(r)can be estimated by:

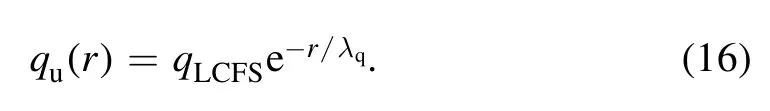
Here the radial power decay length and density decay length are assumed asλq= 0.75 cm andλn= 2×λqin the calculation according to the empirical value in EAST.

4.Modeling result

4.1.Equilibrium configuration dependence of connection length

Figure 3 shows the connection lengthLbetween upstream points on the midplane and reciprocal target points on the UO divertor plate calculated by the field line tracing method for EAST shots #84816–84818 at =t6.1 s.The maximumLis located at the striking point position,which is the connection length between the upstream point on separatrix and target point, andLdecreases with increase of distance to UO divertor corner or moving the upstream point from separatrix to the wall alongRdirection.The difference of connection length profiles on divertor plate for the three shots is due to the different magnetic topologies, or different equilibrium configurations.

4.2.Equilibrium configuration dependence of SOL plasma

Compared with experimental observation, the profiles of plasma density, temperature and particle flux density on the UO divertor plate calculated by the two-point model for EAST shots #84816–84818 at =t6.1 s are shown in figure 4.Here the experimental data is measured by the Langmuir probe on the divertor plate.Overall, the profiles of plasma density,temperature and particle flux density on the divertor target are roughly similar to the experimental observation for the three shots.With equilibrium configuration change from#84816 to#84818, the peak positions of the profiles together with striking point move to the divertor corner for the modeling result,as the two-point model based on the magnetic topology of SOL and the constantLstrongly depends on the equilibrium configuration.The peak positions of the profiles of #84817 agree well with the experiment while the peak positions of other two shots have a little gap with experimental measurement.There are several possible reasons such as the influence of finite radius of ion gyro motion and the incidence angle of magnetic field line to the probe.The modeling target temperature where the distance to UO divertor larger than 15 cm is a little higher than the measurement, which may due to the neglect of charge exchange power loss effects.More details will be discussed in summary.

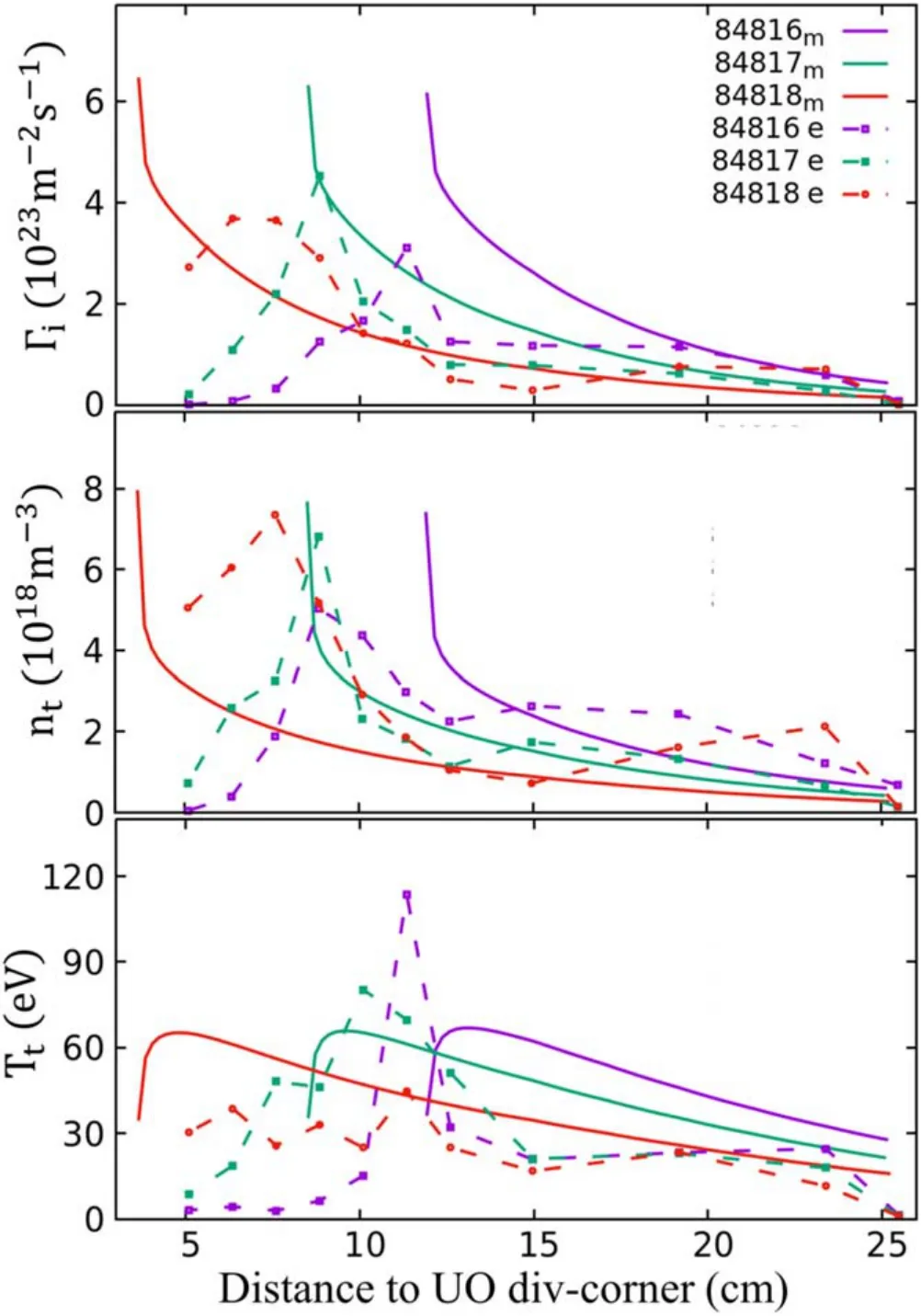
Figure 4.Profiles of (a) particle flux, (b) plasma density and (c)plasma temperature at the UO divertor for EAST shots#84816–84818 with different equilibrium configurations.The symbols with dotted line are experimental data measured by Langmuir probe,and the solid curves are the 2-point modeling results.Here the temperature for the experimental data is electron temperature.

5.Summary

In this paper,we used a fast and light two-point model based on the field line tracing method to investigate the influence of equilibrium configuration on the characteristics of SOL plasma in EAST.The profiles of plasma density,temperature and particle flux density on the divertor target calculated by the model are in reasonable agreement with the experimental observation.With the equilibrium configuration change, the magnetic topology in SOL region will change leading to the change of connection length and striking point shift,resulting in different profiles of plasma parameters on divertor plate.The two-point model can catch the main information of magnetic topology effects, which is helpful to give a qualitative insight into physics of transport process in SOL plasma and interpret the experiments.Furthermore, the model could be used for the real-time analysis as it only needs a very few computing resources and could be combined with other equilibrium code such as HINT [13] to improve the equilibrium calculation in the open field line region.

Due to relative simplicity of the two-point model, the complicated physical process in the SOL plasma such as the vertical transport, the plasma wall interaction cannot be simulated and the modeling result cannot be fully consistent with experimental observation.There is a little gap for the peak positions of plasma parameters profiles on divertor plate between the modeling and experimental observation.Neglecting the measuring error and the spatial resolution of probes,the finite radius of ion gyro motion and the incidence angle of magnetic field line to the probe could make the peak position of saturated ion flux measured by Langmuir probe not the same with modeling result.The gap between the peak heat flux position and the striking point will be counted with experimental database in the future work to correct the model.Moreover, the control parameters such as conduction factor,momentum and power loss factor can be automatically set by experience-based learning in the future analysis.

Acknowledgments

This work was performed on JSPS-CAS Bilateral Joint Research Projects, ‘Control of wall recycling on metallic plasma facing materials in fusion reactor’.This work was supported by the NIFS Collaboration Research Program(Nos.NIFS18KNST130 and NIFS20KNST171).Also, this work was partially supported by ‘PLADyS’, JSPS Core-to-Core Program, A.Advanced Research Networks.