基于ICA的同频信号盲源分离

芦伟东

（国家无线电监测中心哈尔滨监测站，黑龙江 哈尔滨 150010）

0 引言

为了充分用好有限的频谱资源，现代无线电通信常需共用同一频率。在整个频段带宽只有30MHz的短波频段，频率共用更是普遍现象。在日常的短波无线电监测工作中，有时可能在同一个频率上同时收到来自不同发射机的两个或更多个信号混杂在一起的混合信号，这对后续的信号分析工作带来困难。因此，在现有条件下找到合适的同频信号分离方法，具有重要研究意义。无线电监测属于非协作通信，通过监测捕获的信号往往没有先验信息，所以分离监测到的同频信号属于盲源分离的范畴[1]。

1 盲源分离

在一个鸡尾酒会上，多个人一起说话，输入到多个麦克风，如何从混合信号中分离出每个人说话的声音？由此引出了盲源分离问题[2-3]。由于缺乏先验信息，对观测到的信号进行盲分离具有以下两个特点：一是观测信号通过盲分离后得到的输出源信号顺序不确定；二是输出源信号幅度不确定。但这并不影响盲分离的应用，可以通过信号波形得到源信号所携带的主要信息。盲源分离过程如图1所示。

图1 盲源分离流程

绝大部分的盲源分离方法属于无监督学习方法，需要基于某种理论构造目标函数，常被采用的目标函数包括：高阶累积量、最大似然估计、互信息量和负熵等。独立分量分析（ICA，Independent Component Analysis）属于高阶累积量分析方法，是目前解决盲源分离问题的重要方法之一。

2 ICA基本原理

设S（t）为N个统计独立的输入信号，经过A信道传输后，在接收端得到M个观测信号X（t），则

式中，X（t）为M维矢量；S（t）为N维矢量；n（t）为M维加性信道噪声；A为M×N维混合矩阵，且M≤N。Y为解混后得到的信号，ICA传输模型如图2所示。

图2 ICA模型

由图2可知，ICA的主要目标就是要使输出信号Y无限接近源信号S，这实际上就是一个不断寻优的过程，仅需找到矩阵B，使其成为A的最佳估计逆矩阵即可求解出Y。ICA方法还需满足源信号相互统计独立、各矢量均值为零和至多有一个是高斯信号的约束条件。

ICA算法流程如图3所示。其中数据预处理操作的目的是简化算法和消除后续算法执行过程中可能出现的错误，预处理可以分为以下几种类型：一是中心化，对输入变量进行中心化处理，使各矢量均值为零；二是白化，使变量去相关，实现统计独立；三是主成分降维，实现简化算法；四是降噪，消减噪声的影响。

图3 ICA算法流程

ICA的估计方法由目标函数和优化算法组成[4-5]。在指定目标函数的情况下，可以任选随机梯度等经典的优化算法。理想情况下，ICA方法的鲁棒性、一致性等统计性质和算法的收敛速度等算法性质是相互独立的，即对于同一个目标函数可以使用不同的优化算法，同一个优化算法，可以适用于不同的目标函数。ICA算法分类如图4所示，这些算法都是在源信号相互间的统计独立性和非高斯性的基础上建立起来的。

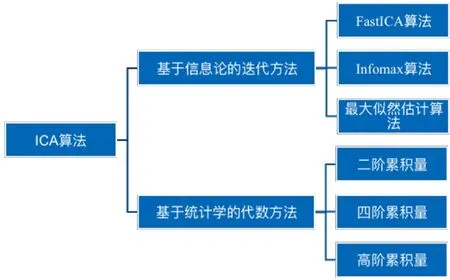
图4 ICA算法分类

其中，FastICA算法已经成为目前盲源分离领域应用最广泛的算法之一。结合当前无线电监测系统硬件系统不易改动的现实情况，寻求仅在软件层面解决同频信号分离的问题，可以尝试将FastICA算法应用实际无线电监测工作中，实现同频信号的分离。

3 FastICA算法仿真

快速独立分量算法（FastICA， Fast Independent Component Algorithm）又称为不动点（Fixed-Point）算法，是在ICA算法的基础上发展起来的，选用了定点迭代的方法，在保证算法稳定性的同时，达到更快的收敛速度。FastICA算法包括基于负熵最大、似然最大和峭度最大等形式，本文应用基于负熵最大的FastICA算法，其优点是可以结合不动点迭代的优良特性和负熵更好的统计特性[6-9]。

FastICA算法的迭代公式为：

式中，E[·]为均值计算；g[·]为非线性函数；X为观察信号；w为分离矩阵向量。

FastICA算法的主要实施步骤：

①对观测信号X去中心化，使其均值为零；

②然后进行白化处理，得到Z=wTX；

③选择一个具有范数的随机向量W；

④更新W←E{Zg（wTZ）}-E{g（wTZ）}w，常用的函数 g 有：g1（y）=tanh（a1y）；g2（y）=y*exp（y2/2）；g3（y）=y3；

⑤标准化，W←w/||w||；

⑥若未收敛，则返回④。

在实际监测过程中分别采集两段比较清晰的模拟语音信号，一个为中文广播，另一个为英文广播，混合后通过FastICA算法进行解混，过程和结果如图5所示。

图5 模拟语音信号解

从图5中可以看出，解混效果良好，达到了信号分离的目的。再分别采集SITOR-ARQ和SITOR-FEC数字音频信号，混合后通过FastICA算法进行解混，结果如图6所示。

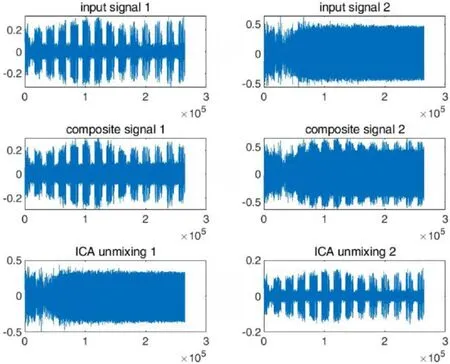
图6 数字信号解混

从图6可以看出，解混效果良好，后续对多路数字信号进行实验也得到了比较理想的结果，在此不再赘述。

4 结束语

本文针对实际监测工作中可能遇到同频信号，无法直接进行后续信号分析，影响工作效率的问题，提出将FastICA算法应用于实际信号分离工作中。在不改变任何硬件设施的前提下，尝试仅通过软件方式解决同频信号分离的问题。对于最常见的双信号混合的情况，分别对模拟语音和数字混合信号进行解混，得到了较理想的仿真实验结果，给同频信号分离提供了一种新的思路。