大跨度充气膜结构形态分析方法研究

成新兴，张 超，牛国平，陈建稳，武宝会

(1．西安西热锅炉环保工程有限公司，陕西 西安 710054；2．南京理工大学 理学院，江苏 南京 210094；3．西安热工研究院有限公司，陕西 西安 710054)

充气膜结构因具有造型新颖多变、气密性好、移动方便、节能环保等特点，在展览馆、体育场、实验室、沼气池、航天飞行器、方舱医院、工业储料场等各类场景均得到应用[1-4]，为满足无组织排放治理的环保要求，众多充气膜封闭料场相继建成，领域遍布电力、煤炭、钢铁、水泥、港口等．因场地及设备条件限制，此类充气膜结构具有外形不规则、大空间和大跨度的特点．

形态分析是充气膜结构设计与分析的重要步骤，分为找形和找态两部分内容．非线性数值计算等方法广泛应用于充气膜找形分析中，近些年又发展出三维摄影测量等试验方法[5-7]．早期文献中找形分析多以等应力曲面为研究对象，采用小弹性模量法，找态分析则通过解析法直接实现[8-10]．

实际工程中的大跨度充气膜结构均为非等应力曲面，预张力难以通过解析解精确确定，此时找态与找形同等重要，采用小弹性模量法难以得到理想解．部分文献中提出了迭代法找态和逆变形法找形的基本思路，但缺乏较系统全面的论述[11-15]．

本文总结充气膜形态分析理论，系统提出一种形态分析方法，通过形面误差分析对结果进行验证，并介绍应用实例．

1 充气膜形态分析理论

充气膜结构通过内外压差使得膜面向外扩张并形成预拉力，进而产生结构刚度来抵御外力，充气膜所受的压力、预张力和外形间存在对应关系，可由薄膜无矩理论推导其解析方程．膜材微小几何变化会使得膜面受力随之变化，呈现出极强的几何非线性特征．

1.1 解析方程

膜单元为柔性结构，具有正交异性、大位移小应变、无抗弯刚度和不能承受压力的特性．

根据薄膜无矩理论可知：

(1)

式中：P为膜面压力；T1、T2为膜面预张力；r1、r2为两个主应力方向的曲率半径．

根据肥皂泡原理，充气膜造型总是向表面积最小方向发展．从几何角度上讲，膜面曲率变化引起预张力变化，最终形成具有等应力或不等应力的初始形态曲面．

高斯曲率是衡量空间曲面的重要特征：

K=λ1×λ2

(2)

式中，λ1、λ2为主曲率．

(1)当K>0时，为正高斯曲率曲面，如球面．

(2)当K<0时，为负高斯曲率曲面，如双曲面．

(3)当K=0时，为零高斯曲率曲面，如圆柱面．

在理想边界条件下，充气膜结构随着压力变化会形成等应力曲面．根据公式(1)推导可得

对于矩形平面：

(3)

式中：T为膜面预张力；x、y、z为空间坐标；a、b为充气膜短板和长边方向长度．

当z=f时，x=y=0，

(4)

式中，f为充气膜高度.

对于圆形平面：

(5)

式中：r为充气膜曲率半径，d为充气膜底面直径．

对于圆柱形曲面：

(6)

1.2 非线性有限元法

实际工程中的充气膜结构应力分布往往不是均匀的，非线性有限元法因具有计算量大、计算精度高的优点被广泛应用．

充气膜结构的平衡方程可表示为

[K]{ΔU}={P}-{F}

(7)

式中，[K]、{ΔU}、{P}、{F}分别为总刚度矩阵、总位移矩阵、气压作用的总节点荷载力向量和等效总节点力向量．

采用牛顿—拉普森迭代方法对公式(7)方程组进行求解构成充气膜有限元形态分析的主要内容．

对于图1中给出的理想解析曲面可以是等应力曲面，形态分析常采用小弹性模量法、从平面初始状态迭代求解，分析重点在于找形，曲面预张力值、压力与曲面形状一一对应．

图1 高斯曲率曲面Fig.1 Gaussian curvature surface

一般非理想解析曲面不存在等应力曲面，对于不等应力的平衡曲面，曲面预张力值及曲面形状均不规则且难以直接确定，找态与找形变得同等重要．有限元平衡迭代只有在与最终形态相接近的“初始形”和“初始态”条件下求解才能逼近目标形态．此时，采用小模量分析找到的曲面面积远大于初始假定曲面面积，由于假定的初始形态存在误差，直接采用实际弹性模量计算又很难收敛，需要首先获得接近初始形态的收敛解，再改为实际弹性模量并求得最终平衡形态．

2 形态分析方法

实际工程应用的充气膜结构要求内部大空间且造型丰富，多为不等应力曲面，因此不等应力曲面的形态分析方法更具有实践价值．

采用的充气膜结构形态分析流程归纳如图2所示.

图2 形态分析流程图Fig.2 Flow chart of morphological analysis

首先采用若干理想高斯面组合构建接近目标形的初始形，根据解析方法求得分片预张力作为初始态，然后通过非线性有限元法求解预应力及变形，将求得的变形值逆向施加改变初始形，对逆变形后有限元模型再次迭代求解，最终求得平衡形态．

下文以边界条件为矩形的大跨度充气膜结构为例对形态分析方法进行详细论述．

2.1 构建初始形

长方体充气膜的简化构型如图3所示，可由三个等半径的圆柱面组合而成．此构型的缺陷在于柱面间的结合处形成一个钝边，有限元计算发现此处不易收敛，很难求得理想的平衡解．

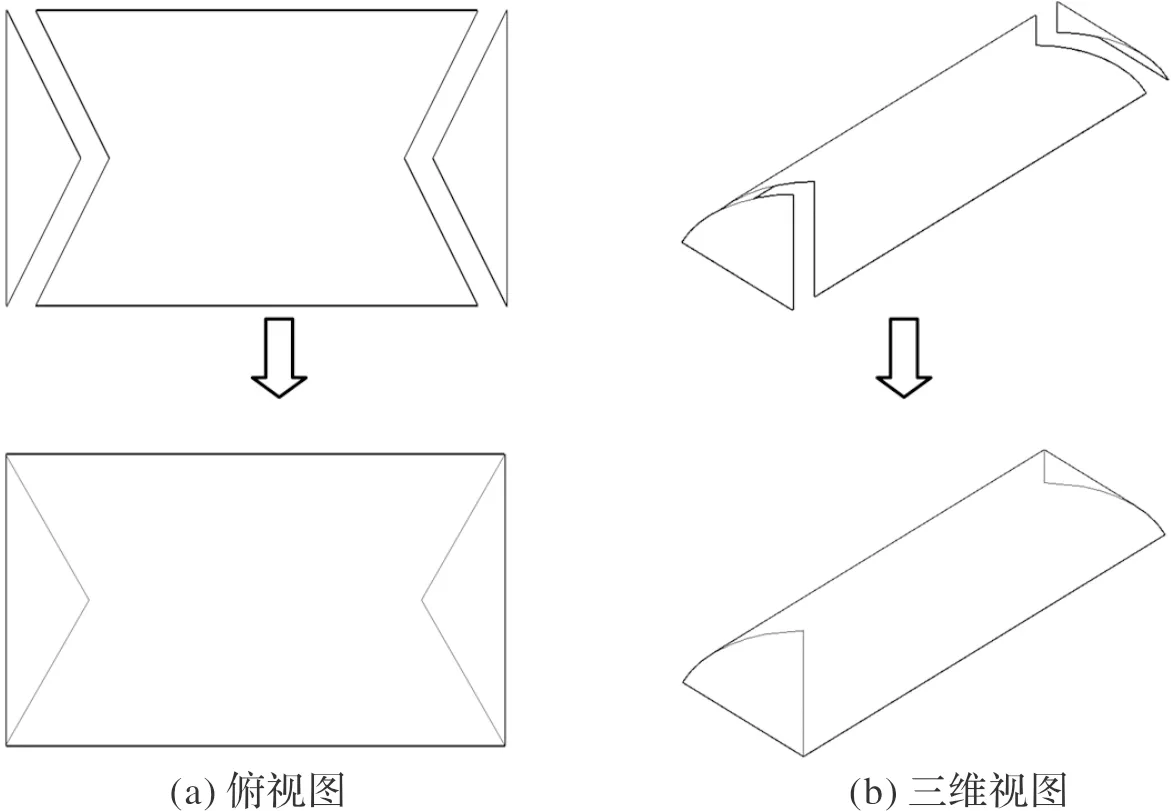
图3 简化构型Fig.3 Simplified configuration

故提出图4所示柱面+平滑过渡球面的优化初始构型，在柱面间的结合处增加过渡球面，使得组合构型交界处更加平滑顺畅，更易实现大型充气膜结构有限元求解的收敛．

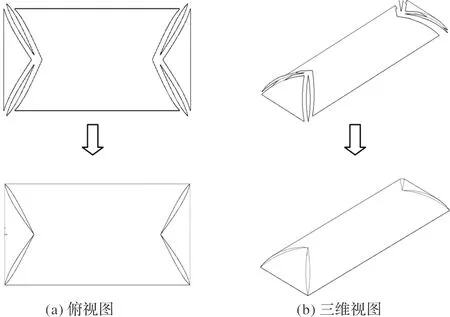
图4 优化构型Fig.4 Optimized configuration

通过解析方法可推算优化构型中的过渡球面及柱面半径计算公式，以柱面角部最低点和最高点为基点作球面与柱面相切，由其相交线分割的区域即为过渡球面．

过渡球面半径：

(8)

式中，a为充气膜短边方向长度．

柱面半径：

(9)

2.2 假定初始态

根据1.1节解析方法可推导出矢高和压力条件确定的分片膜面的预张力，以此作为充气膜结构的初始态进一步求解．

联立公式(5)、(8)，球面初始预张力为

(10)

联立公式(6)、(9)，柱面初始预张力为

(11)

2.3 有限元分析

根据解析法确定的初始形态建立数值计算模型，充气膜模型长度300 m，跨度100 m，高度35 m．如图5所示．为满足计算精度要求，共划分96 354个膜单元网格，膜单元厚度1 mm．经试算，弹性模量取值量级为×108N/mm2，略小于实际值．膜面压力取150 Pa．采用通用有限元软件中的牛顿—拉普森迭代法进行非线性分析，计算考虑大变形效应．

图5 有限元模型Fig.5 Finite element model

由于分片假定的膜面初应力存在误差，将首次非线性分析后的膜面应力结果设置为膜面初应力再次分析，经数次应力回代后计算结果趋于稳定，膜面von mises应力如图6所示．

图6 初始形迭代后von mises应力Fig.6 Von mises stress after initial shape iteration

将迭代稳定后的变形计算结果逆向施加于初始形求得逆位移形，对逆位移形再次进行非线性分析．逆位移形的初始态仍采用分片假定的解析解，经数次迭代计算至结果稳定，逆变形迭代后von mises应力如图7所示．

图7 逆变形迭代后von mises应力Fig.7 Von mises stress after inverse deformation iteration

将逆位移形计算后的变形结果正向施加即求得最终平衡形．初始形、逆位移形和平衡形的有限元模型对比如图8所示，从形状上看，逆位移形分片过渡段呈现弧度减小甚至内凹的趋势，逆位移形的大跨度柱面呈现两端略高中间略低的趋势；平衡形的分片过渡区域平滑圆润且无棱角，与工程实际情况高度吻合．

图8 逆变形前后形态对比Fig.8 Morphological comparison before and after inverse deformation

2.4 平衡态结果

对平衡形再次验算，计算收敛迅速，平衡态的von mises应力和变形结果如图9、图10所示．

图9 平衡态von mises应力Fig.9 Von Mises stress in equilibrium state

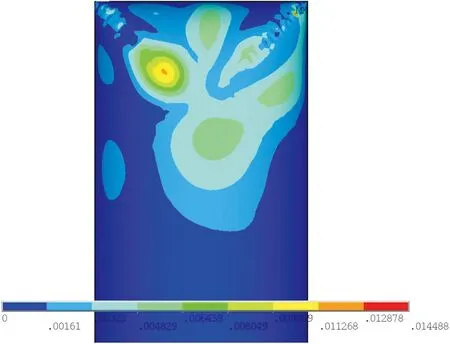
图10 平衡态变形Fig.10 Deformation in equilibrium state

有限元模型最小von mises应力为0.723 ×106N/mm2，最大von mises应力为13.4×106N/mm2，最大变形为0.014 5 m．最大应力、最小应力及最大变形均位于充气膜四角，即分片接缝处；模型中部膜面应力及变形趋于一致．

2.5 形面误差分析

采用最大变形δmax、平均变形μ、变形均方差σ三个特征参数来分析形面误差．

将充气膜结构初始构型与非线性有限元计算后的平衡态构型进行比较，对有限元模型中48 380个节点变形进行数据处理，得出初始构型的形面误差，如表1所示．

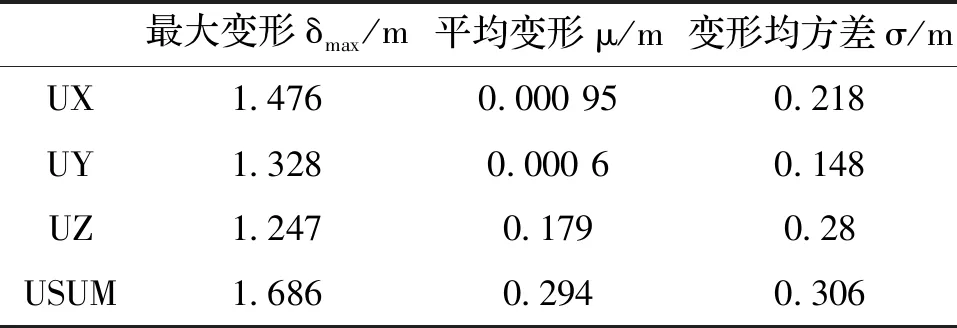
表1 初始构型形面误差Tab.1 Surface error of initial configuration

从表1可以看出：合力方向最大变形δmax为1.686 m、平均变形μ为0.294 m、变形均方差σ为0.306 m．初始构型中存在局部形态变位较大，整体形面变位误差约为0.3 m．初始构型与平衡构型存在分米级的形面误差，且局部区域形面误差更大．

对平衡态构型再次进行非线性有限元形态分析，并对计算分析前后的形面数据进行比较，得出平衡构型的形面误差，如表2所示．

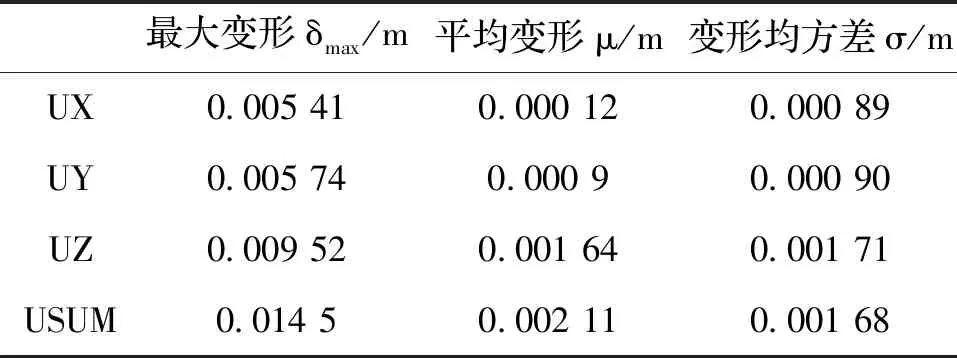
表2 平衡构型形面误差Tab.2 Surface error of equilibrium configuration

从表2可以看出：合力方向最大变形δmax为0.014 5 m、平均变形μ为0.002 11 m、变形均方差σ为0.001 68 m．平衡构型中整体形态变位误差约为0.002 m．初始构型与平衡构型的形面误差已控制在毫米级，此误差在百米级跨度的充气膜结构中可忽略，说明本文所采用的形态分析方法的计算精度可满足工程实际需要，其形态分析结果可应用在找形分析、荷载分析和裁切分析各阶段中．

3 大跨度充气膜结构应用实例

某储料场长宽尺寸为253 m×70.4 m，场内设置门式堆取料设施，采用充气膜结构对储料场进行封闭．膜材参数如下.

厚度：1.08±0.07 mm

拉伸强度：(经向/纬向)≥7 500/7 000 N/5 cm

涂层材料：PVDF

透光率：膜材透光率达到5%以上．

适用温度：低温≥-30 ℃，高温≤70 ℃

该实例方案剖面图如图11所示．

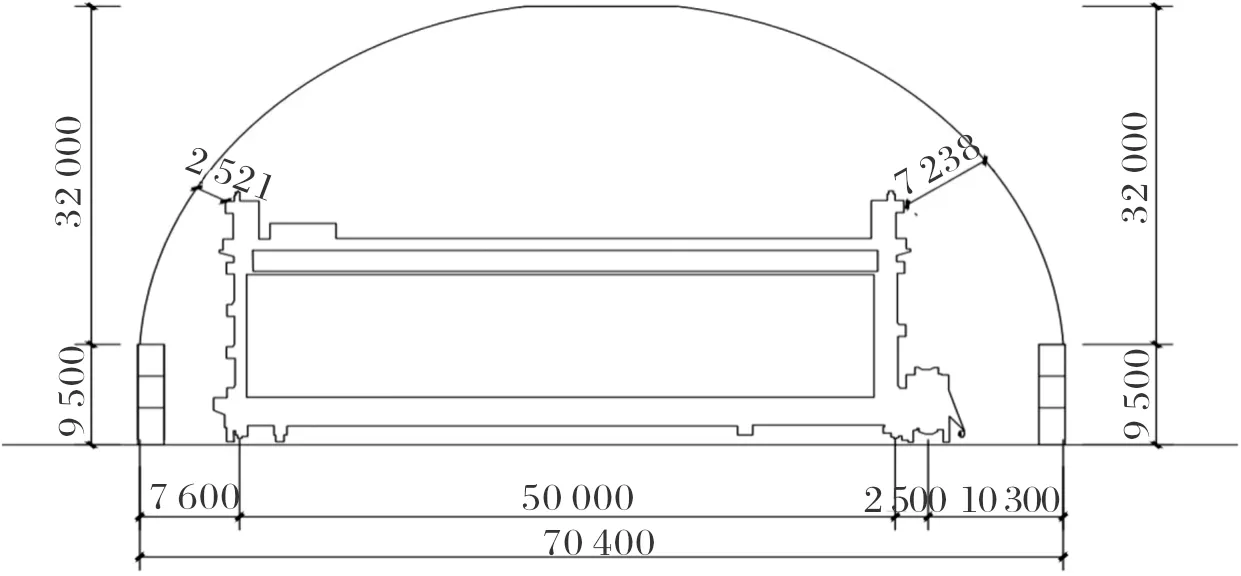
图11 方案剖面图(单位：mm)Fig.11 Scheme section(Unit:mm)

经形态分析后，膜面裁切成品如图12所示．

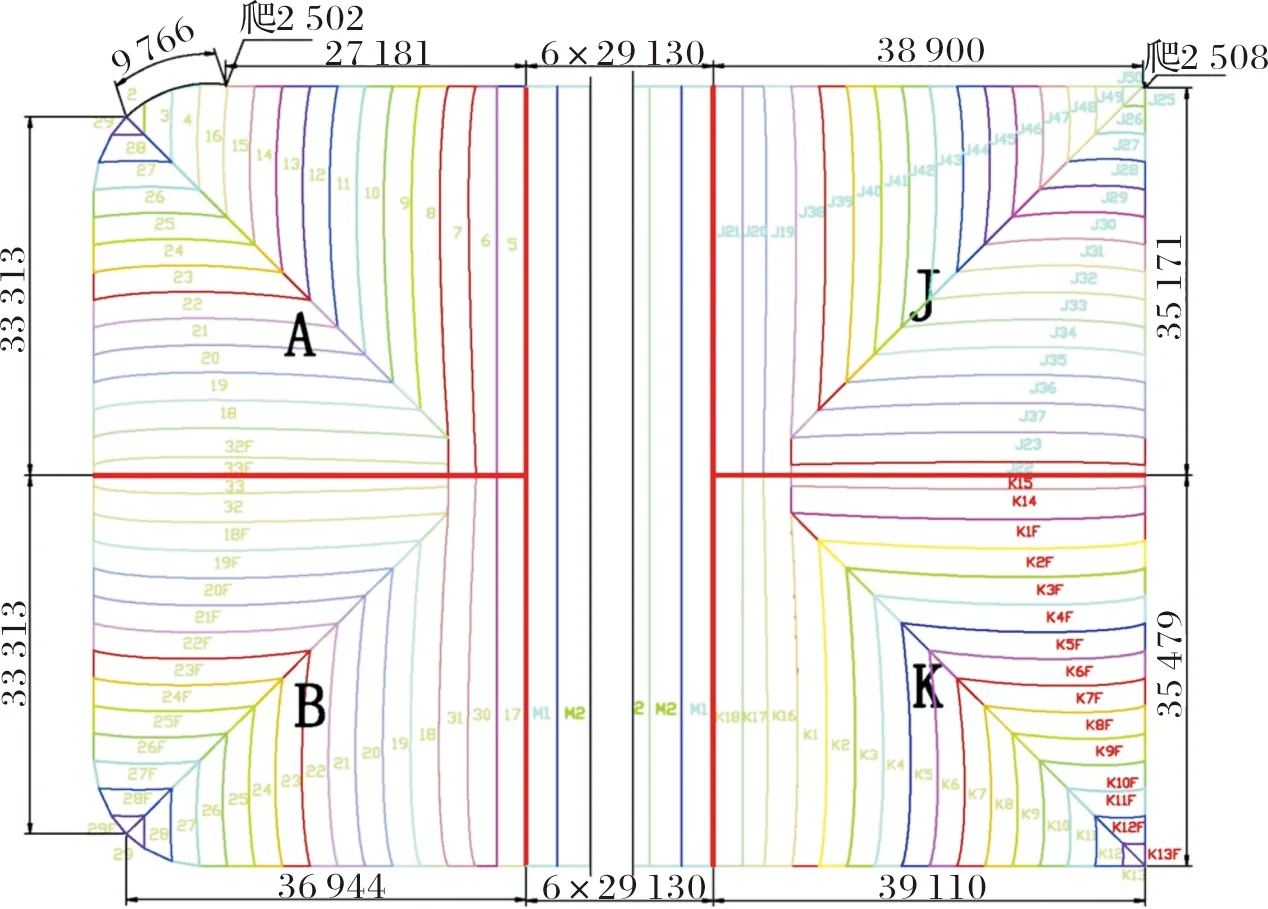
图12 膜面裁切成品(单位：mm)Fig.12 Membrane cutting product(Unit:mm)

应用实例现场照片如图13所示．

图13 现场照片Fig.13 Scene photo

4 结论

本文阐述一种针对大跨度充气膜结构的形态分析方法，采用解析计算与数值模拟相结合的方式，求解充气膜平衡形态，结论如下：

(1)经分析验证，平衡态构型下形面误差均方差值为0.001 68 m，计算精度满足要求．

(2)本文方法经实例验证，可满足工程实际需要．

(3)本文中形态分析未考虑索的作用，标准化程度高且应用范围广的充气膜结构设计方法尚需进一步深入研究．