基于模拟目标的测量雷达实战化训练方法研究

蒋立民,王 成

(中国人民解放军91245部队，辽宁 葫芦岛 125001)

0 引言

精密跟踪测量雷达是武器装备测试过程中测量系统重要的组成部分，具有测角精度高、数据率高等特点。能够全天候、远距离实时跟踪测量空中飞行目标，能够提供目标角度、距离、径向速度和RCS(目标的雷达散射截面积)等测量元素信息，主要用于武器装备试验中目标外弹道的精确测量，为武器装备试验过程的控制、指挥和决策提供有效支撑。目前，测量雷达训练主要有以下两种途径：1)利用脱离装备的模拟训练器对操作手进行训练，此方法训练成本低，可重复性好，但训练的真实度不高，针对性不强，训练效果难以达到预期；2)利用实际雷达装备跟踪布设站点周边过航飞机等目标进行训练，此方法训练，装备操作感真实，但存在重复性差、缺乏针对性等缺点。随着科技发展，武器装备试验中被测目标呈现高速、机动、大航程、低可探测性等特点，试验的背景条件日趋复杂、风险系数急剧增大、测量精度、安全性和可靠性要求越来越高，这就对雷达操管人员的装备操管水平提出了更高的要求，急需采用贴近实战的训练方法对雷达操管人员进行训练，提高其操作装备搜索、捕获、稳定跟踪被测目标的能力。

为此，提出了基于模拟目标的测量雷达实战化训练方法，方法是以计算机仿真技术为基础，通过构建训练合作目标的运动轨迹模型、RCS特性模型，利用软件编程的方式将目标轨迹与特性模型封装成训练目标模型，并利用测量雷达本身的目标模拟器，在测量雷达上实现模拟目标、真实装备的半实物仿真跟踪，进而达到近实战化训练的效果。目前多数测量雷达均具有目标模拟器，因此，本文着重介绍训练目标模型的构建。

1 目标运动轨迹模型构建

目标运动轨迹建模有很多种方法，根据不同目标类型采用不同的方法，针对本文测量雷达实战化训练方法对合作目标的需求，研究了两种不同目标运动轨迹模型的构建方法，两种目标分别是：无动力目标，如传统火炮发射后出膛的弹丸；动力目标，如各种导弹、火箭弹。

1.1 无动力目标运动轨迹模型构建

无动力目标发射出膛后的运动轨迹，可采用传统的弹道微分方程构建。为便于研究，构建过程中，假设无动力目标飞行过程中仅受到地球引力(方向不变)与大气阻力作用，无动力目标为标准轴对称体，在理想气象背景下，建立以发射点O为坐标系原点，以地球引力方向为y轴，引力相反方向为正，以射向面与过O点垂直y轴平面的交线为x轴，沿射向为正，按照右手法则确定z轴，建立发射坐标系，用o-xyz表示。

规定大气阻力加速度α，建立基于发射坐标系，以时间为自变量的无动力目标运动方程组：

(1)

因研究过程中设定目标是轴对称体，假设攻角为0度，此时大气阻力矢量与目标对称轴重合，质心在目标对称轴上，大气阻力必定通过质心，这样可以认为作用在目标上的力都过质心，目标可作为一个质点来处理。规定：目标射出后重新落回到发射点水平面上的一点为落点，根据公式(1)变换可得发射直角坐标系的目标质心运动方程组如下：

(2)

据式(2)，在气象条件为：气压pon=1 000 hPa；气温ton=20 ℃；密度ρon=1.206 kg/m3；地面虚温τon=288.9 K；相对湿度φ=50%；声速cson=341.1 m/s；无风；密度函数H(y)在y<10 000 m时采用经验公式H(y)=(1-2.1904×10-5×y)4.4；阻力函数G(v,cs)中阻力系数cxon(Ma)根据43年阻力定律取值，在给定目标不同初始速度、发射点海拔高度、射角、弹形系数时，规定高低攻角和侧向攻角均为0°，通过仿真可得到目标不同的弹道曲线，如图1所示。

图1 仿真运动轨迹图

从两个弹道曲线可以看出，同一无动力目标弹道主要由发射初速度、发射角度和弹道系数等确定。采用构建的无动力目标运动轨迹模型生成的仿真弹道曲线与掌握的预估理论弹道曲线基本一致，方法可行。

1.2 动力目标运动轨迹模型构建

动力目标与无动力目标的区别一是动力目标在发射后，本身具有动力系统，目标受力情况不同；二是动力目标可根据需要，进行空中机动。轨迹模型构建过程中，建立以发射点O为坐标系原点，以地球引力方向为y轴，引力相反方向为正，以射向面与过O点垂直y轴平面的交线为x轴，沿射向为正，按照右手法则确定z轴，建立发射坐标系，用o-xyz表示。为便于研究，将目标运动轨迹进行分段处理，包括动力段，无动力段，机动段，二次动力段4个阶段。其中动力段为目标发射后靠自身动力系统加速飞行的阶段，理想条件下认为该阶段目标受到本身动力系统的推力、大气摩擦阻力、地球引力，该阶段可根据目标初始速度、射向角度、动力飞行时间、合加速度等参数求得目标轨迹点位坐标；无动力段为目标动力系统停止工作后，进行带有一定速度的类抛物运动阶段，理想条件下认为该阶段目标受到大气摩擦阻力和地球引力作用，该阶段可根据目标阶段初始速度、最大射高、射向角度、无动力飞行时间、阻力加速度等参数求得目标轨迹点位坐标；机动阶段为目标进行机动飞行的阶段，飞行中的目标进行机动方式很多，可通过自身辅助动力系统给目标施加一个变向加速度，也可通过目标弹翼、舵机来改变目标航向，该阶段可根据目标阶段初始速度、预设航迹坐标点位、等参数求得目标轨迹点位坐标；二次动力段为目标飞行过程中动力系统再次工作阶段，理想条件下认为该阶段目标受到本身动力系统的推力、大气摩擦阻力、地球引力，该阶段可根据目标阶段初始速度、攻向角度、被攻击目标点位坐标、合加速度等参数求得目标轨迹点位坐标，运动轨迹分段示意图如图2所示。

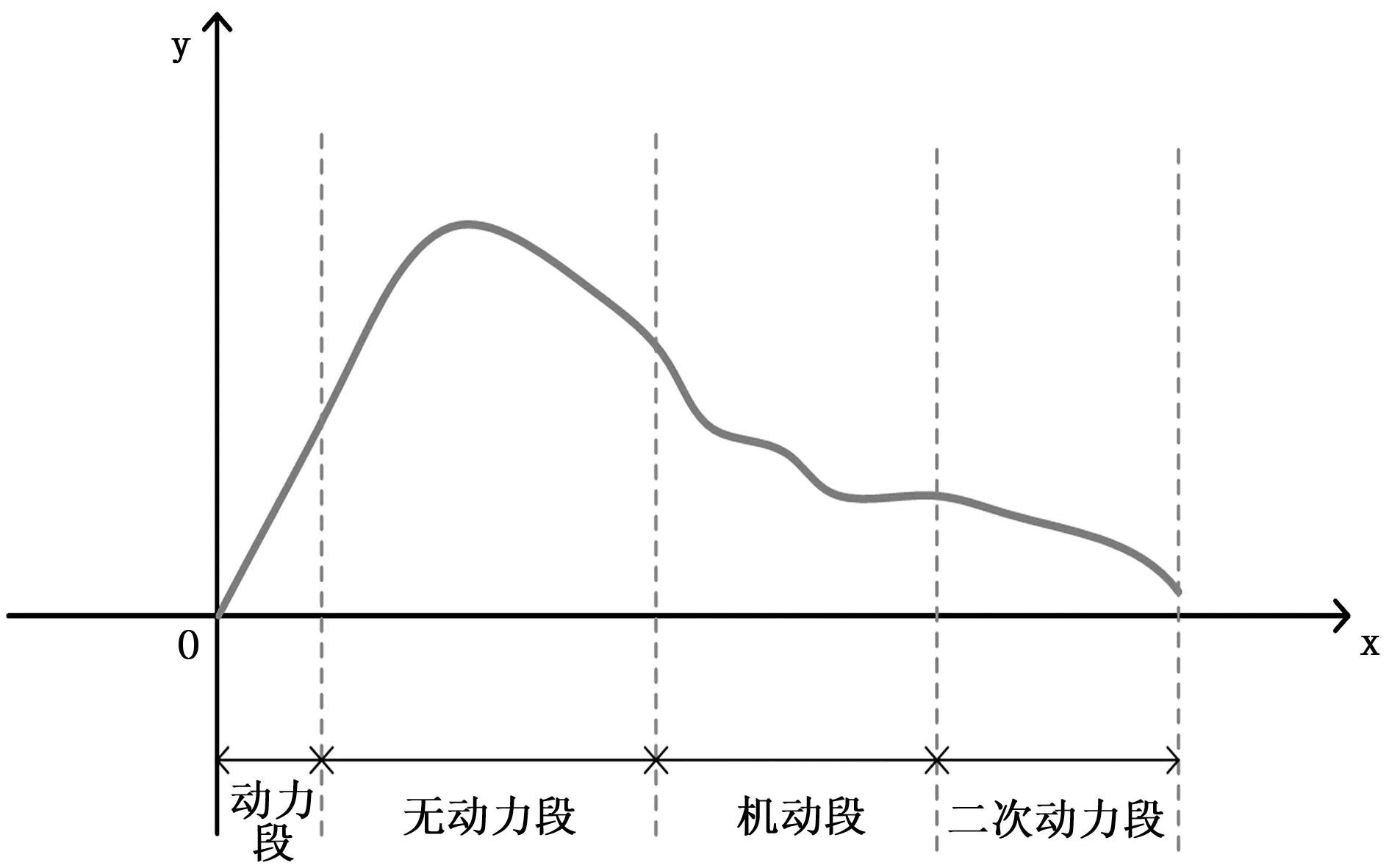
图2 动力目标轨迹分段示意图

目标在发射坐标系下的点位坐标确定后，按照发射坐标系到地心直角坐标系的转换关系对点位坐标进行转换，设发射坐标系点位(xf,yf,zf)，地心直角坐标系点位(xd,yd,zd)，根据下式：

(3)

其中：(xof,yof,zof)为发射原点的地心坐标，λof、φof、θ分别为发射原点的经度、纬度、发射方位角(即射向)，Rx(θ)、Ry(θ)、Rz(θ)值如下：

通过转换得到目标运动轨迹地心直角坐标系下的点位集(xd,yd,zd)，但是由于采用算法及过程参数设置的关系，不可避免的导致运动轨迹不平滑，因此还需对点位数据集进行平滑处理以得到最终的运动轨迹模型，本文采用的是kalman滤波方法进行数据平滑处理，根据(xd,yd,zd)的前两次测量值z1和z2求得kalman滤波的初值，即有：

(4)

(5)

按照滤波协方差矩阵初始值，计算预测协方差矩阵，可得：

(6)

若已知kalman增益Kk+1：

(7)

则可按照下式计算滤波协方差：

(8)

由状态滤波值和状态转移矩阵，按下式可计算状态预测值，即为：

(9)

由状态预测值、测量值和kalman增益就可以计算kalman滤波值，即为:

(10)

经过平滑处理后得到所需的目标轨迹(xi,yi,zi)。如图3所示，曲线代表采用模型构建的目标运动轨迹射程、高程变化趋势，两条曲线分别代表原始数据和平滑处理后的数据，从图中能够明显看到平滑处理的效果。

图3 平滑处理前后数据曲线对比图

2 目标RCS特性模型构建

实际的空中目标跟踪测量过程中，影响RCS测量结果的因素主要有目标尺寸、运动轨迹、观测角度、姿态变化等，本文研究目标是针对导弹及炮弹弹丸这种形状简单的目标，这类目标的姿态变化幅度通常较小，变化平缓，主要取决于观测角，因此，研究过程中姿态根据时刻射向简单处理，不做过多考虑。RCS特性模型构建主要分3个步骤：1)构建目标几何尺寸比例模型；2)利用计算方法获得目标静态RCS序列；3)根据目标运动轨迹、观测角等信息仿真获得目标动态RCS序列。

2.1 目标几何尺寸比例模型构建

目标几何尺寸比例模型构建主要采用计算机图形技术来实现，本文采用的曲面造型技术，即利用参数曲面来描述目标的几何模型，具体采用的B样条曲线曲面的方法实现。B样条曲线可以设计各种曲线曲面，是广泛使用的几何形状数学设计方法。其k次B样条曲线方程为：

(11)

式中pi,i=1,......,n为控制顶点，按照顺序连接生成B样条多边形。Fi,k(t),i=1,......,n为k次B样条基函数，Fi,k(t)是一个k次分段多项式，其表达式：

(12)

式中，

(13)

利用B样条曲线方程构建的弹丸目标模型如图4所示。

图4 弹丸目标模型图

2.2 目标静态RCS序列

目标几何尺寸比例模型构建完成后，利用相关的计算方法可得出目标静态RCS。本文研究的目标模型针对火炮弹丸目标和无翼导弹目标，因此在研究过程中，目标模型均可看作简单圆柱体弹身与锥体弹头或椭球体弹头的组合体，为便于研究，忽略弹体与弹头结合部位在计算中带来的增量值。

1)圆柱体RCS计算：

圆柱体RCS可由物理光学法近似计算，在给定其几何尺寸参数的情况下，对于如图5所示的参数圆柱体，可根据式(14)求得。

图5 圆柱几何参数示意图

圆柱体RCS近似计算公式为：

(14)

式中，L为圆柱长；A为圆柱截面半径；λ为波长；K=2π/λ。

2)锥体RCS计算：

特定时刻可将弹头近似看作无限锥体，当电磁波轴向射到弹头时，如图6所示，会产生尖顶散射，可根据式(15)求得RCS。

图6 锥体柱几何参数示意图

无限锥体RCS近似计算公式为：

(15)

式中，λ为波长；δ为半圆锥角。

3)椭球体RCS计算：

通常情况下，电磁波的射向并非沿着轴向，此时弹头RCS计算不能采用无限锥体方法计算，可采用几何光学法进行计算，椭球体几何尺寸参数如图7所示，根据公式(16)求得。

图7 椭球几何参数示意图

椭球体RCS近似计算公式为：

(16)

采用以上3种方法计算RCS时，默认目标材质为金属材质，其中在计算圆柱体RCS时需注意，入射波方向偏离表面较远时，由物理光学法得来的圆柱RCS计算公式失效，需要采用几何绕射理论来修正。最终获得的目标RCS近似值为：

σi=σ1i+σ2i或σi=σ1i+σ3i

(17)

以弹丸目标为例，以弹头方向为0度，弹尾方向为180度，建立弹丸外型、尺寸模型，计算不同观测角度下弹丸RCS值如图8所示。

图8 不同观测角度弹丸RCS计算值

2.3 目标动态RCS序列

目标静态RCS序列获得后，利用VC软件编程技术，根据目标运动轨迹、速度信息、测量雷达站址信息、雷达数据率等信息，仿真得到目标动态RCS序列，仿真流程如图9所示。

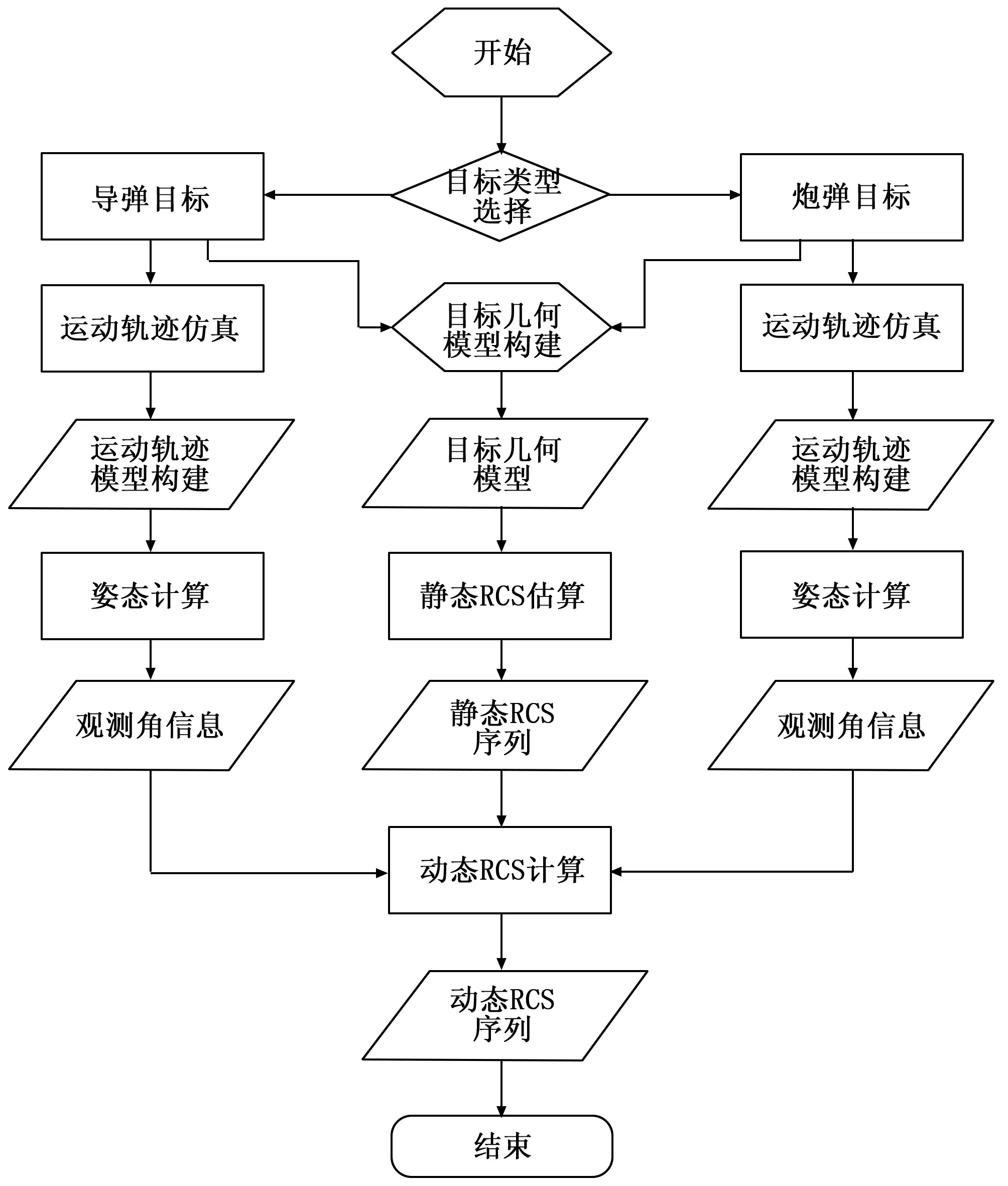
图9 目标动态RCS获取流程示意图

过程中，因研究针对的目标类型均可看作轴对称体，所以在目标运动轨迹模型构建完成后，根据目标运动轨迹变化趋势即可得到目标空中姿态，结合测量雷达站址信息、电磁波射向等信息就可以得到对应时刻的射向角，根据时刻、射向角就可以在RCS静态序列当作提取对应的RCS值，作为该时刻的动态RCS值。仿真过程中未考虑实际过程中的大气、测量误差、环境噪声的干扰，在实际应用当中，应根据实际情况采集大气、环境噪声等加以添加应用，使动态RCS更接近实际。图10为某弹丸目标利用上述方法获得的动态RCS仿真数据与该弹丸在实际飞行中的实测RCS数据。

图10 RCS仿真数据与实测数据比较图

从图10可以看出，未考虑干扰因素的仿真数据和实际测量数据还是存在差异。由于弹丸目标本身特性决定了其雷达回波偏弱，再者，实际测量数据采用的是标准球RCS比较法获得，测量本身即存在误差，实测数据并不能作为绝对真值来考量。考虑的动态RCS仅作为仿真训练使用，因此通过上述研究方法获得的目标动态RCS序列，能够满足为测量雷达仿真训练提供模拟目标的需求。

3 研究结果应用

目标的运动轨迹模型构建方法和RCS特性模型构建方法研究完成，并通过仿真方式验证后，如何将研究结果应用到测量雷达跟踪训练当中成为需要解决的问题。本文利用VC编程结合OpenGL绘图技术来实现对研究成功的运用。

3.1 运动轨迹模型构建方法应用

根据前文运动轨迹模型构建方法，利用Microsoft Visual C++程序开发平台，开发轨迹模型设计软件，用过软件将构建方法转化为实际运用，软件流程如图11所示。软件界面如图12所示。

图11 运动轨迹设计软件流程图

图12 目标运动轨迹设计软件界面

3.2 RCS模型构建方法运用

根据前文目标RCS特性模型构建方法，利用Microsoft Visual C++程序开发平台，开发目标RCS特性模型设计软件，通过软件将构建方法转化为实际运用，软件流程如图13所示。

图13 训练用目标模型设计软件流程图

4 训练方法在雷达装备上的实现

在模拟训练合作目标模型构建完成后，模型封装包如何与雷达结合，开展基于模拟目标、实际雷达装备的半实物仿真跟踪，是训练方法在雷达装备上得以实现的关键。通常的测量雷达都带有目标模拟器，可通过目标模拟器实现。本文方法在某型测量雷达上通过目标模拟器，很好实现了模型封装包如何与雷达结合。

目标模拟器包含波形生成控制、衰减控制、天线方向调制、多普勒频移、起伏调制以及数据收发处理等功能。其原理如图14所示。

图14 雷达目标模拟器原理图

实现过程为：首先，雷达数传系统将目标模型封装数据包加载，并发送给目标模拟器，目标模拟器对目标的模型数据包进行解析处理，生成目标的仿真回波，依据运动轨迹模型以及雷测装备站点坐标等信息，对仿真模拟回波进行多普勒频移、起伏调制等处理；然后，根据目标的运动轨迹模型、雷达波相对目标射向角度、距离波门位置、统一时间序列下的RCS特性等参数信息，对仿真模拟回波进行天线方向图函数调制、距离衰减、回波强度调制等处理；最后，将仿真模拟回波与雷达实际工作环境背景噪声回波叠加，在实际雷达装备上生成接近被模拟目标实际情况的雷达回波，供雷达装备在特定的时空域内搜索、发现、识别、捕获和跟踪测量，实现基于模拟目标实际雷达装备的实战化训练。具体在某型测量雷达上实际实现效果如图15所示。

图15 模拟目标在雷达上回波显示

5 结束语

为解决测量雷达实战化训练时，存在的由于缺少训练合作目标，导致训练真实性差、训练效果不理想等问题，本文通过研究，利用成熟的数学算法结合计算机仿真方式构建了针对炮弹弹丸和导弹类目标的运动轨迹模型、RCS特性模型，在此基础上，利用Microsoft Visual C++编程实现了目标运动轨迹模型和RCS特性模型实际应用，开发了测量雷达模拟训练目标设计软件。通过该软件设计的模拟目标，结合测量雷达目标模拟器，在测量雷达上实现了基于模拟目标的测量雷达实战化训练，该训练方法很好解决了测量雷达跟踪训练过程中缺少贴近实战的合作目标，训练效果不理想的问题，目前，该训练方法已经在某型测量雷达上投入使用，实际应用效果表明，该方法不但对测量雷达操作人员具有实战化训练价值，还可以根据实际跟踪测量任务中，目标的理论弹道、目标几何尺寸设计生成模拟目标，进行跟踪测量任务前的测量演练，演练对保证后续的实际跟踪测量任务具体显著效果，提高了测量任务成功率。研究成果还可推广至所有测量雷达装备上，对于测量雷达具有较好的实用价值。