基于非线性压缩变换的某型航空发动机整机试车排故分析

张 瑞,程传义,张云鹏,王诗彬,黄 海

(1.中国航发沈阳发动机研究所，沈阳 200240;2.西安交通大学 机械工程学院，西安 710049)

0 引言

航空发动机是一种在极其恶劣的服役环境下运行的机械设备，即运行于高速、高温、重载、强扰动等环境下，在这种复杂的工况下，加之其高精密复杂的结构，发动机的故障频繁发生[1-2]。如何诊断发动机并减少其故障频率是近年来一直关注的难题。机械设备运行会产生振动信号，振动信号中往往包含设备的状态信息，如何从复杂的振动信号中提取出有用的状态信息用于状态监测与故障诊断至关重要[3-4]。航空发动机由于服役要求，在经过起飞-巡航-降落不同工作状态时，转速会随时间变化，转速的变化会导致振动信号的瞬时频率具有时变性，即振动信号具有变化的瞬时频率，当航空发动机的转速快速变化时，振动信号的瞬时频率也会快速变化，呈现强时变特征[5-6]。此外，即使机械设备在静止状态下运行时，断裂、碰摩、冲击等故障也会导致产生随时间变化的刚度、阻尼等，从而导致振动信号的瞬时频率也会随时间变化[7-8]。航空发动机振动信号的时变特性增加了其分析的难度，如何从复杂的非平稳信号中获取有用的状态信息是一直在研究的课题。

时频分析方法是分析时变非平稳信号非常有用的工具，因为它能够提供一个直观的时频结构[9]。与传统的时域分析、频域分析相比，时频分析将信号从单一的时域或者频域拓展至时频域，同时以时间和频率为自变量、能量大小为因变量，绘制时频图，描绘信号的瞬时频率随时间变化的规律[10-11]。对于航空发动机时变非平稳的振动信号，时频分析能够提取出信号瞬时频率的变化规律，为航空发动机的状态监测与故障诊断提供有效的帮助。

航空发动机复杂的结构导致振动信号的传递路径也十分复杂，加之故障早期的特征信号本身就非常微弱，所以我们采集到的振动信号中的特征信号往往会比较微弱。如何从大量的噪声干扰中识别微弱且快变的故障信号特征对于航空发动机的状态监测与故障诊断十分重要[12]。非线性压缩变换采用“匹配增强”策略的匹配时频分析思想，通过相互关联的两个时频表示的协同作用，不仅突破传统时频分析方法的幅值相关性，实现微弱信号成分增强，而且压缩传统时频表示对强时变非平稳信号较宽的频带分布，提高时频聚集性[13-14]。非线性压缩变换的微弱信号增强能力以及较高的时频聚集性能够在航空发动机早期故障信号特征识别与诊断中发挥重要作用。

本文基于非线性压缩变换，对某次试车试验中的某型航空发动机振动信号进行分析，从而对该发动机可能存在的故障进行排查与猜测，并且进一步验证了非线性压缩变换在航空发动机实际试车信号分析中的有效性与实用性。

1 非线性压缩变换

本节将通过原理公式以及示意图来介绍非线性压缩变换，并说明其对微弱信号特征的增强以及对时频聚集性的提高。

首先，设x∈L2(R)，窗函数为g(t)的短时傅里叶变换为:

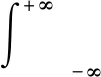
(1)

为了使时间分辨率与频率分辨率之积达到最小值，本文所采用的窗函数均为高斯窗函数，其公式如下：

gσ(t)=(πσ2)-1/4e-t2/2σ2

(2)

式中，参数σ为高斯窗函数的方差，可以控制其宽度。

受同步压缩变换[15-16]中瞬时频率估计算子计算过程的启发，非线性压缩变换定义为短时傅里叶变换与导窗函数短时傅里叶变换之比：

(3)

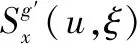
通过上述分析可知，对于抽水蓄能电站，寻找机组及公用设备汛期冷却水备用水源具有相当的难度。但是从相对合理、可靠、安全及经济方面综合考虑，结合上述3个方案的论述，可以采用方案2中的密闭式自循环供水系统（冷却器布置在尾水隧洞内）作为抽水蓄能电站机组及公用设备汛期备用水源设置方案。在上库或下库为天然河道，存在汛期流道内水质含沙量急剧增大可能影响机组及公用设备冷却水供应的情况时，应在可研设计阶段开展相关研究工作，论证电站机组及公用设备汛期冷却水备用水源设置的可行性。

当被分析信号为纯谐波信号时，即：

xh(t)=Aei2πf0t

(4)

则:

i2πf0·Sx(u,ξ)

(5)

因此:

(6)

该式表明，非线性压缩变换Px(u,ξ)与信号幅值无关，当ξ→2πf0时，|Px(u,ξ)|将快速增大。同时，由于当ξ→2πf0时时频系数的快速增大，时频图的能量主要聚集在瞬时频率附近，从而增强了时频图的能量聚集性。

接下来通过简单仿真信号的非线性压缩变换过程图来说明非线性压缩变换在微弱信号增强与时频聚集性提升方面的有效性。

对于仿真信号x(t)=x1(t)+x2(t)，其中:

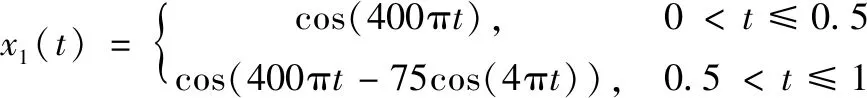
(7)

该信号由两部分组成，且其中信号成分x2(t)的幅值只有x1(t)的0.01倍，为微弱信号成分，信号的瞬时频率如图1(a)所示。该信号的短时傅里叶变换与导窗函数短时傅里叶变换时频图分别如图1(b)与图1(c)所示。可以发现短时傅里叶变换时频图在瞬时频率附近具有极大值，导窗函数短时傅里叶变换时频图在瞬时频率附近具有极小值，那么二者之比则可以得到在瞬时频率处系数很大，其余位置系数快速减小的非线性压缩变换时频图，如图1(d)所示，且由于非线性压缩变换的幅值无关性，原本在短时傅里叶变换时频图中没有显示出来的微弱信号成分也得以显示。通过图1(b)与图1(d)的对比，非线性压缩变换相对于传统的短时傅里叶变换的微弱特征增强能力与高时频聚集性得以验证。

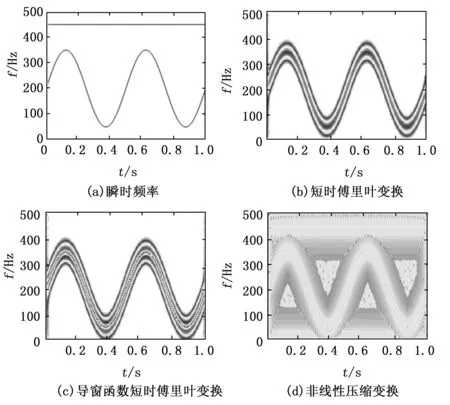
图1 仿真信号瞬时频率，短时傅里叶变换、导窗函数短时傅里叶变换、非线性压缩变换时频图

2 航空发动机试车试验流程

对于本次某型航空发动机试车试验，我们分为振动信号获取、振动信号分析以及故障诊断三个流程来进行，具体流程示意图如图2所示。

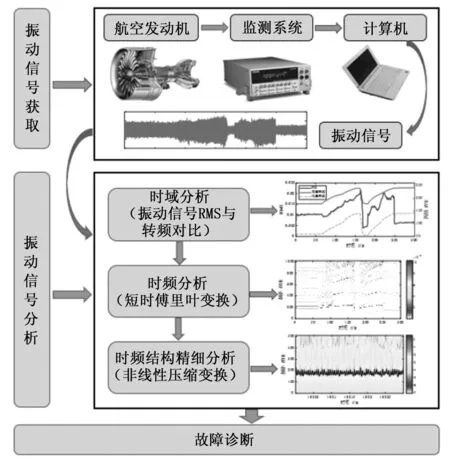
图2 航空发动机整机试车试验流程图

首先是信号获取。我们在某型航空发动机各测点上布置传感器，并通过数据采集系统来获取振动信号。

然后是信号分析。首先我们通过发动机高低压转速与振动信号的RMS对比来分析信号的整体振动情况，然后通过短时傅里叶变换观察信号的整体时频结构，最后采用非线性压缩变换对振动信号中的关键片段进行精细分析。

最后根据信号分析的结果，并航空发动机的结构与理论知识对其进行故障诊断。

3 振动信号分析具体过程及分析结果

本节将按照上一节的振动信号分析流程，对某型航空发动机某次地面试车试验采集到的振动信号进行分析。本次试车试验通过在在各支点轴承座、进气机匣、中介机匣以及后机匣上布置测点采集振动信号，采样频率为8 192 Hz。接下来我们针对其中振动幅值最大的振动信号(即所在测点振动最剧烈)，取其前300 s的数据进行分析。

首先对信号进行时域分析，主要是通过计算振动信号随时间变化的RMS值，并与高低压转频进行对比，从而观察振动信号幅值在变转速过程中的变化情况。振动信号时域波形图如图3所示，RMS曲线与高低压转频曲线如图4所示，从图中我们可以发现，随着高低压转频的变化，振动信号幅值存在小状态突增(即转速较低的情况下振动幅值突然增大，如图4中时刻①所示)与大状态突降(即转速较高的情况下振动幅值突然降低，如图4中时刻②所示)现象。之后我们将对这两个现象进行主要分析。

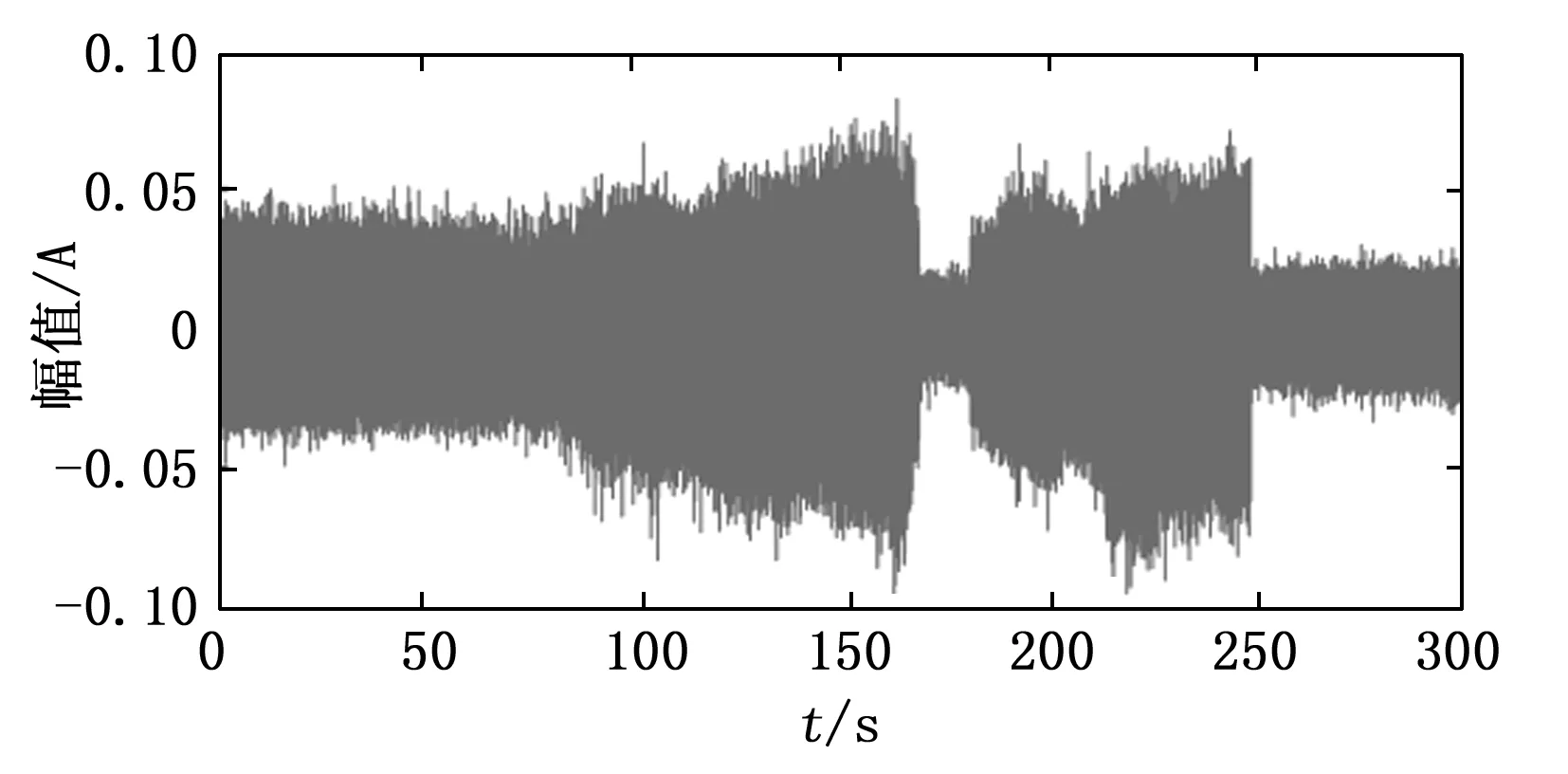
图3 振动信号整体波形图

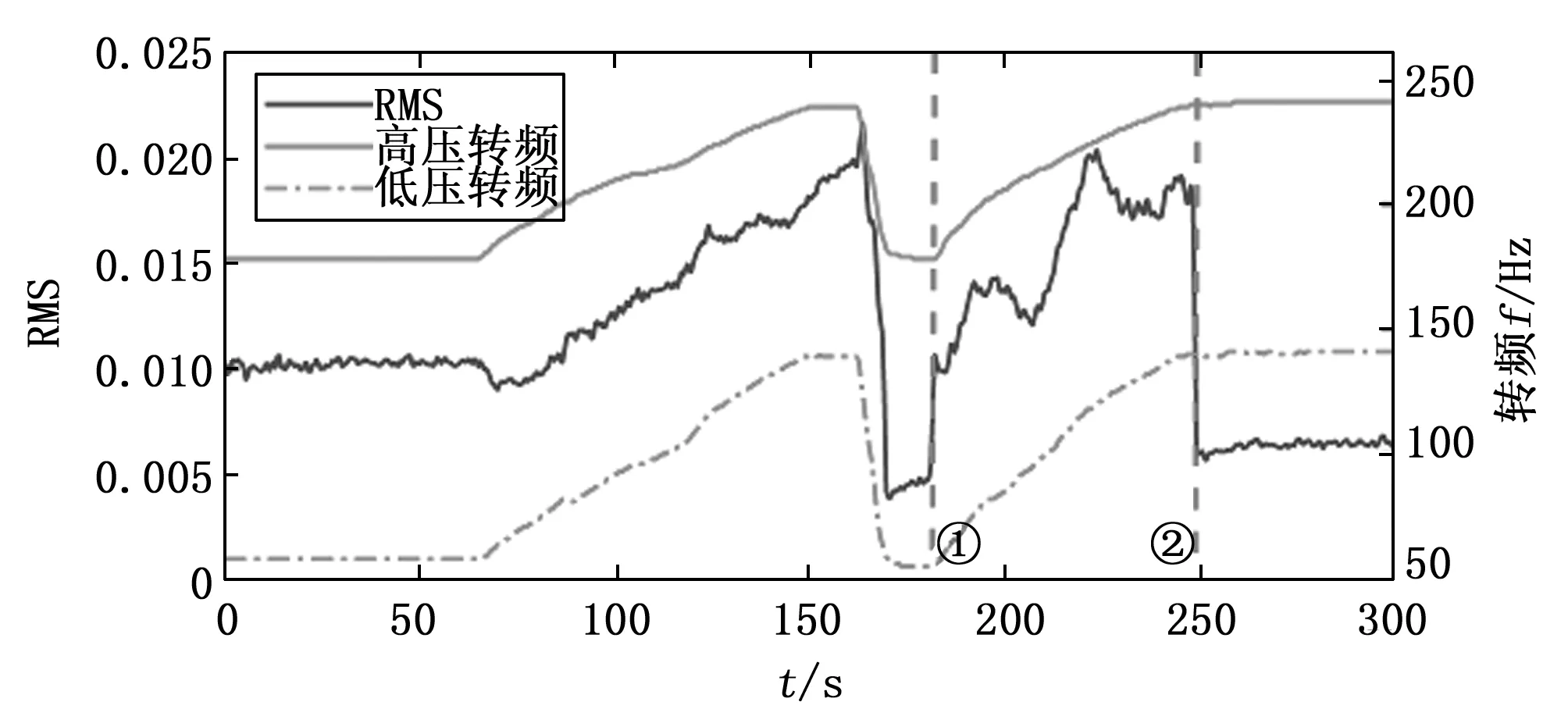
图4 振动信号RMS与高低压转频对比图

然后对振动信号进行时频分析，观察其整体的时频结构。我们首先采用短时傅里叶变换对采集到的振动信号进行整体分析，得到的时频图在较低频率范围内的视图如图5所示。时频图中，高压转频及其倍频幅值比较明显，而低压转频及其倍频幅值则基本没有显示。继而，我们提取高压转频附近的能量，得到高压转频能量曲线图，如图6所示。从该能量曲线图中，我们能明显看出高压转频附近的能量在与RMS曲线相近的时刻存在突增与突降。所以我们初步猜测振动信号幅值的小状态突增与大状态突降与高压工频有关。

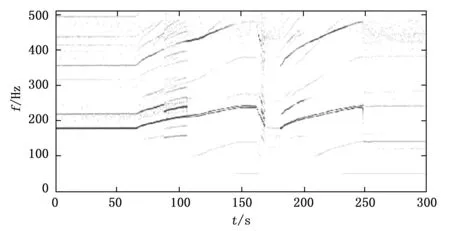
图5 振动信号整体时频图

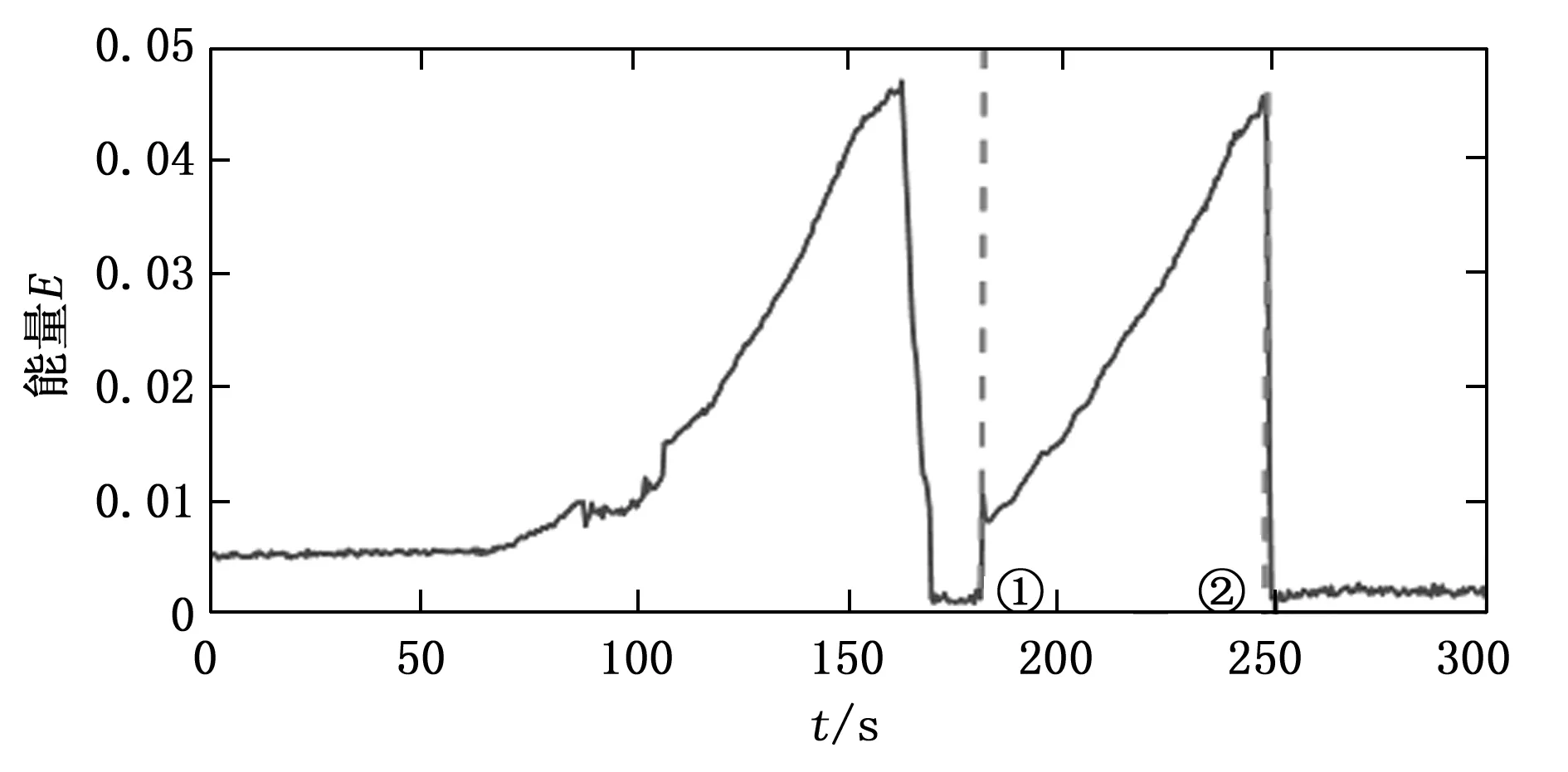
图6 振动信号高压转频附近能量曲线

为了更好地观察信号在发生幅值突变时瞬时频率结构的变化，我们采用非线性压缩变换分别分析小状态突增与大状态突降前后3 s的信号片段，对比观察信号幅值突变前后高压转频附近瞬时频率结构的变化。小状态突增前后(180～183 s)与大状态突降前后(247～250 s)信号片段的时域波形图分别如图7与图9所示，非线性压缩变换时频图分别如图8与图10所示，图中还分别画出了突增前与突增后的局部视图。通过对比，我们可以发现小状态突增后与大状态突降前的信号在高压转频附近存在周期性波动的瞬时频率，而小状态突增前与大状态突降后的信号瞬时频率中则没有这种结构。

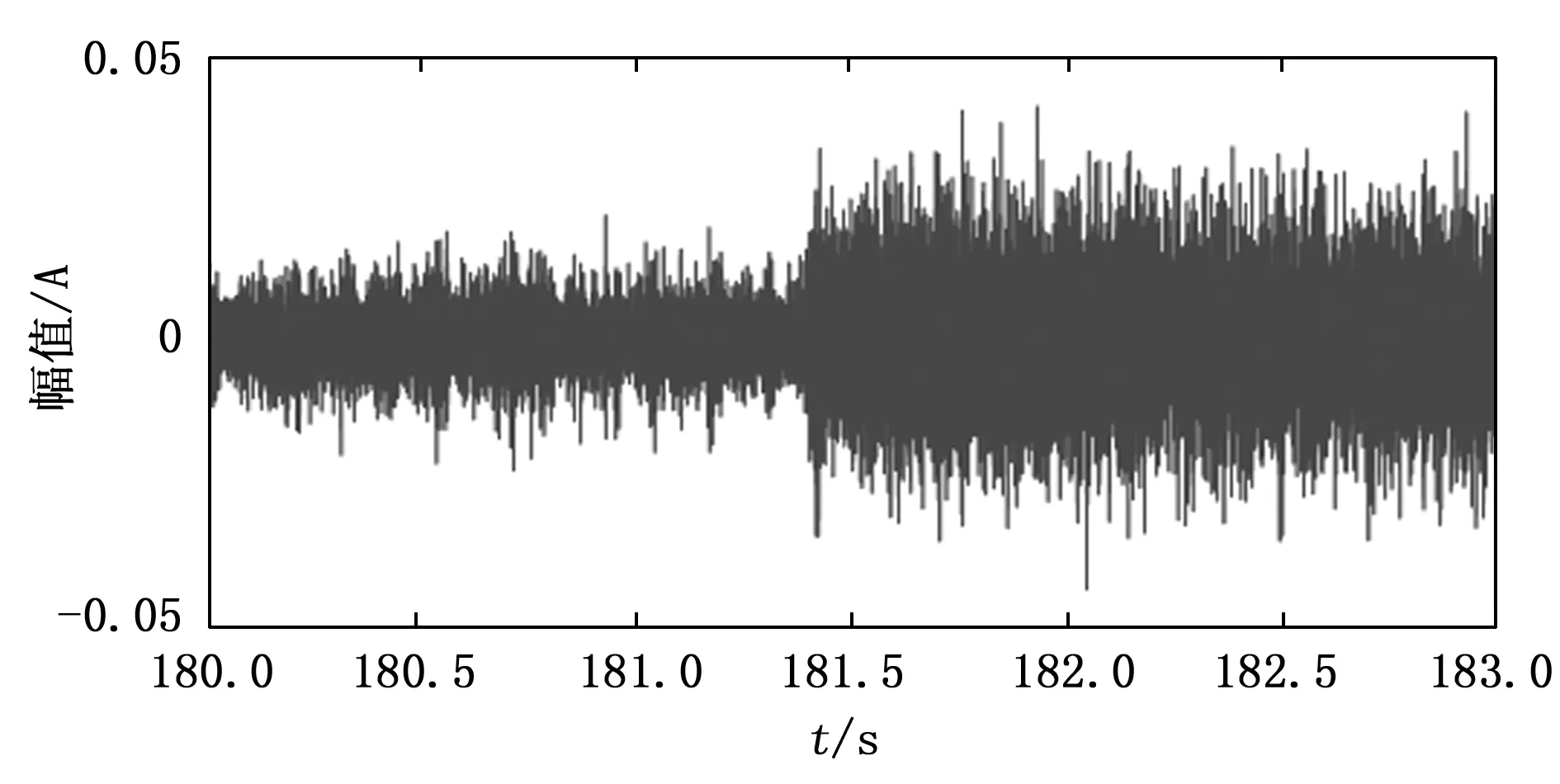
图7 小状态突增前后信号片段

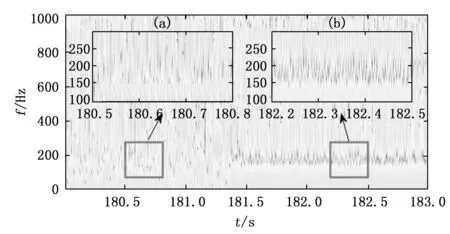
图8 小状态突增前后非线性压缩变换时频图

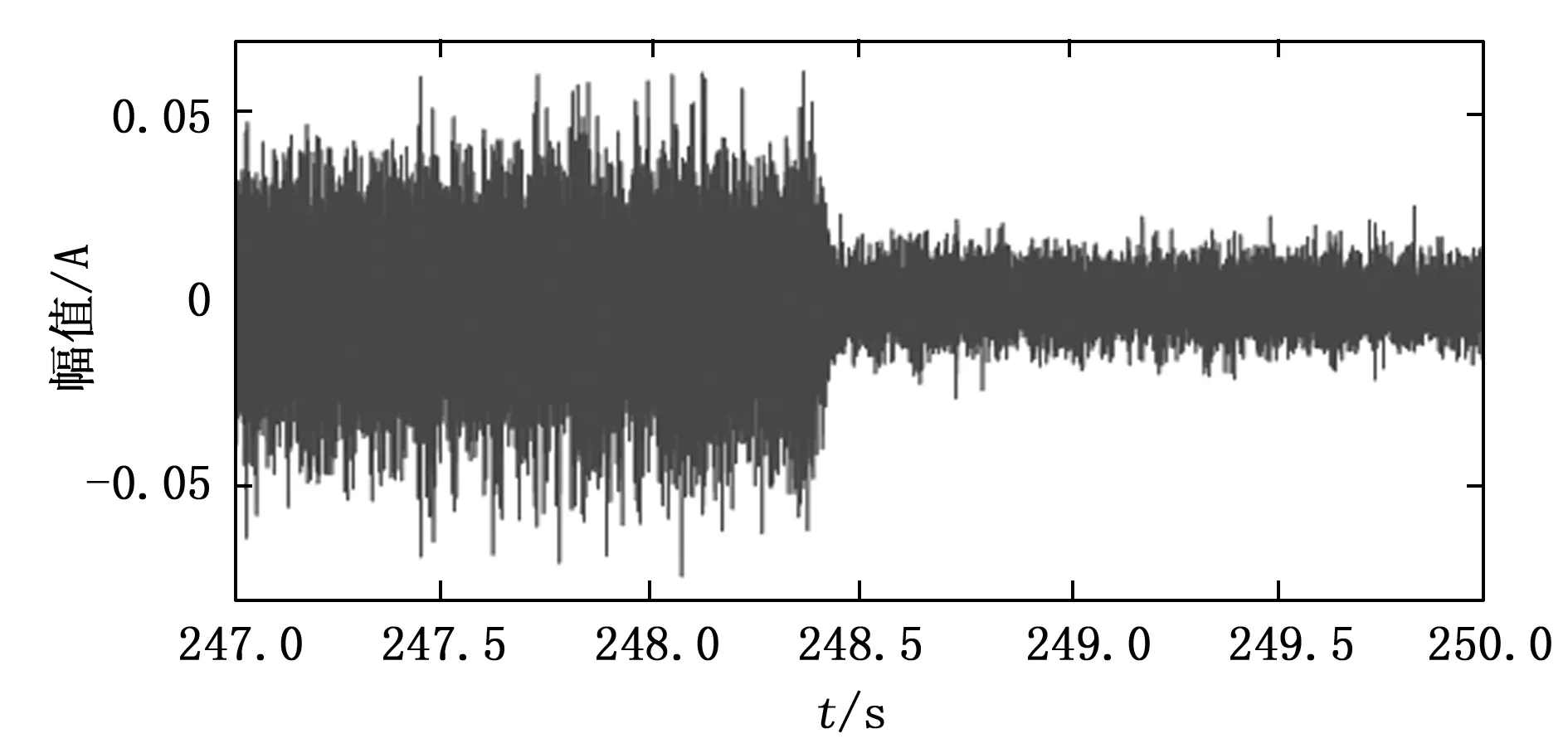
图9 大状态突降前后信号片段

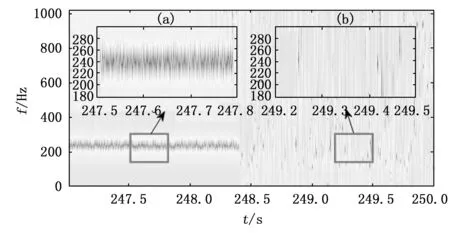
图10 大状态突降前后非线性压缩变换时频图

接下来我们具体分析上述周期性波动的瞬时频率结构，先以小状态突增后的信号为例进行说明。取181.5～182.5 s的信号片段进行分析，该信号的频谱图如图11所示，图中与高压转频对应的频率成分幅值非常明显。对其进行非线性压缩变换分析，得到的时频图如图12所示，为了更好地体现瞬时频率的结构，图12中仅展示了时长为0.3 s的局部视图，图中瞬时频率的周期性变化非常明显。然后采用脊线搜索算法[17]对该时频图进行脊线搜索，得到的时频脊线及如图13所示(为了更好地展现瞬时频率的结构，这里仍然仅展示了时长为0.3 s的局部视图)，且时频脊线的平均值与高压转频相当。接着对提取出的时频脊线进行频谱分析，得到如图14所示的频谱图，图中与高压转频相同的频率幅值非常明显，说明该信号片段存在以高压转频为基频又以高压转频为调制频率的调频现象。

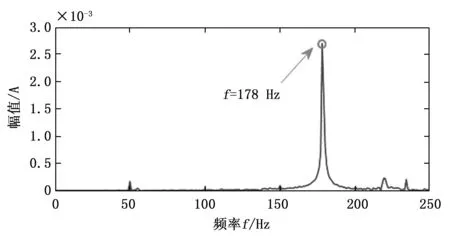
图11 突增后信号片段频谱图

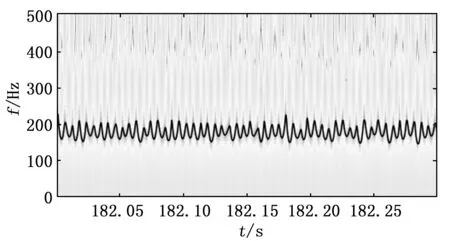
图12 突增后信号片段非线性压缩变换时频图

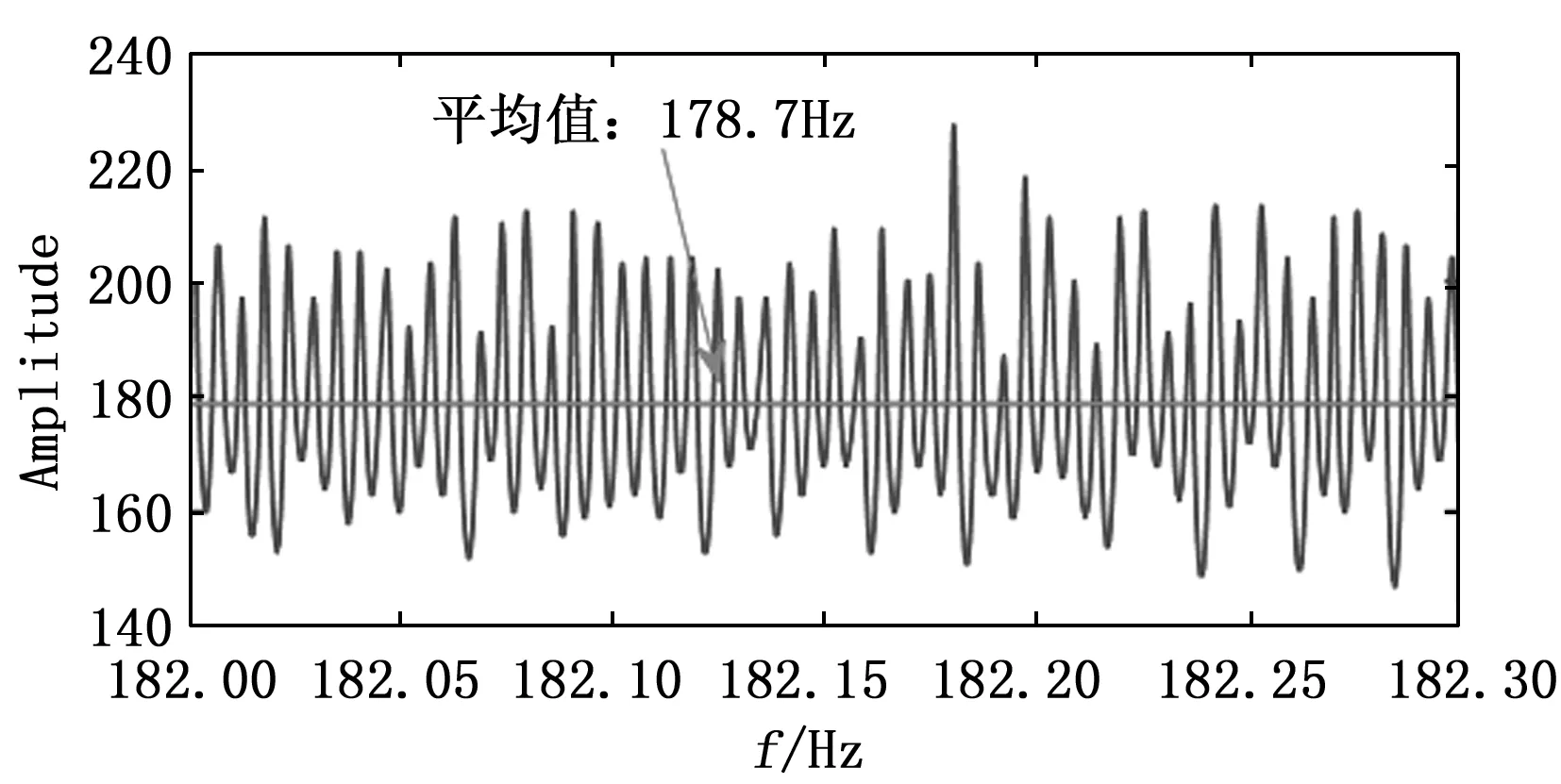
图13 高压转频附近脊线图

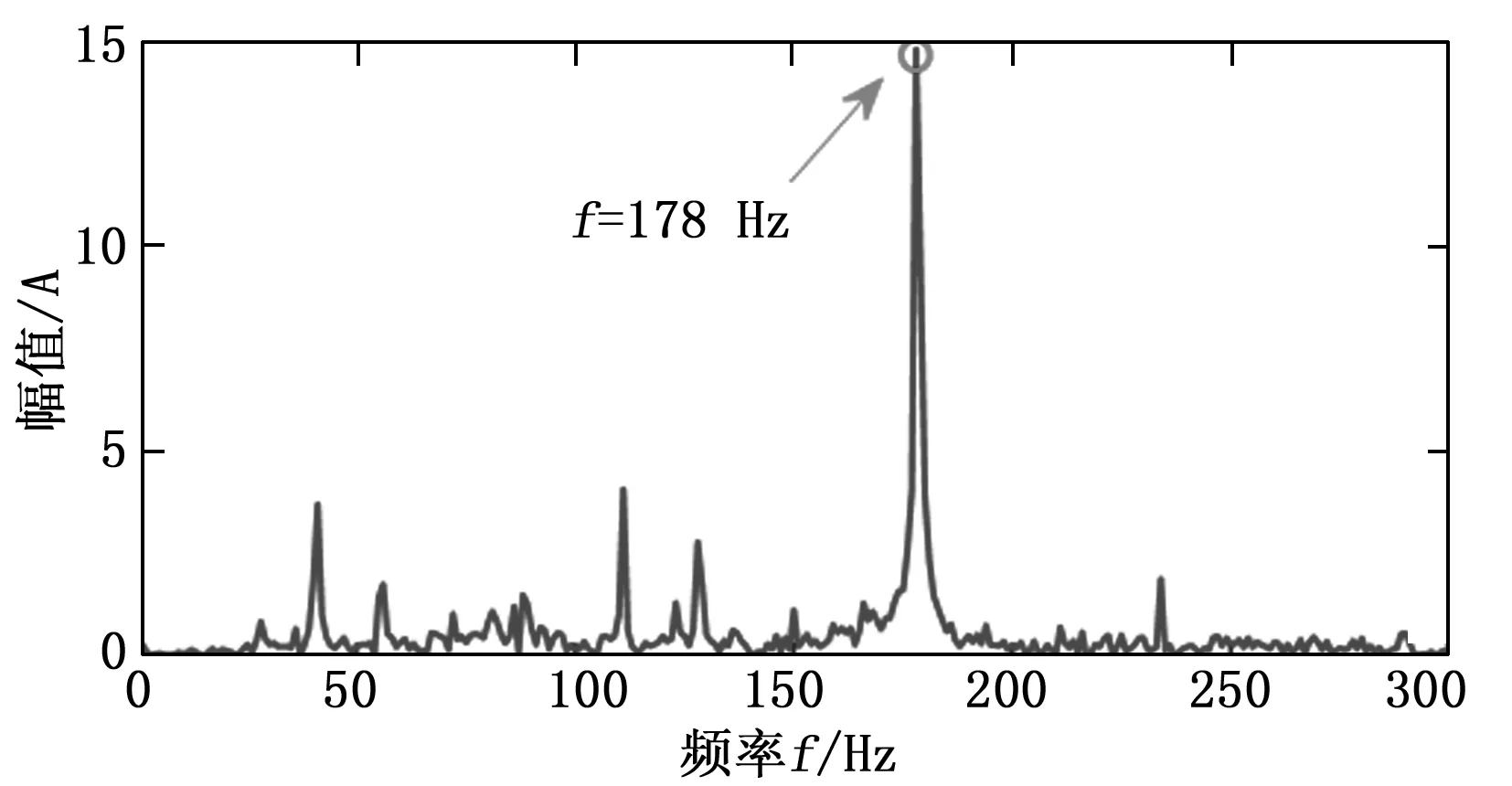
图14 高压转频附近脊线频谱图

对大状态突降前的信号片段(247～248 s)进行相同的分析步骤，得到的频谱图、非线性压缩变换时频图、高压转频附近时频脊线以及脊线频谱图分别如图15～18所示。经过分析也得到与小状态突增相似的结论，即大状态突降前的信号片段中也存在以高压转频为基频，又以高压转频为调制频率的调频现象。

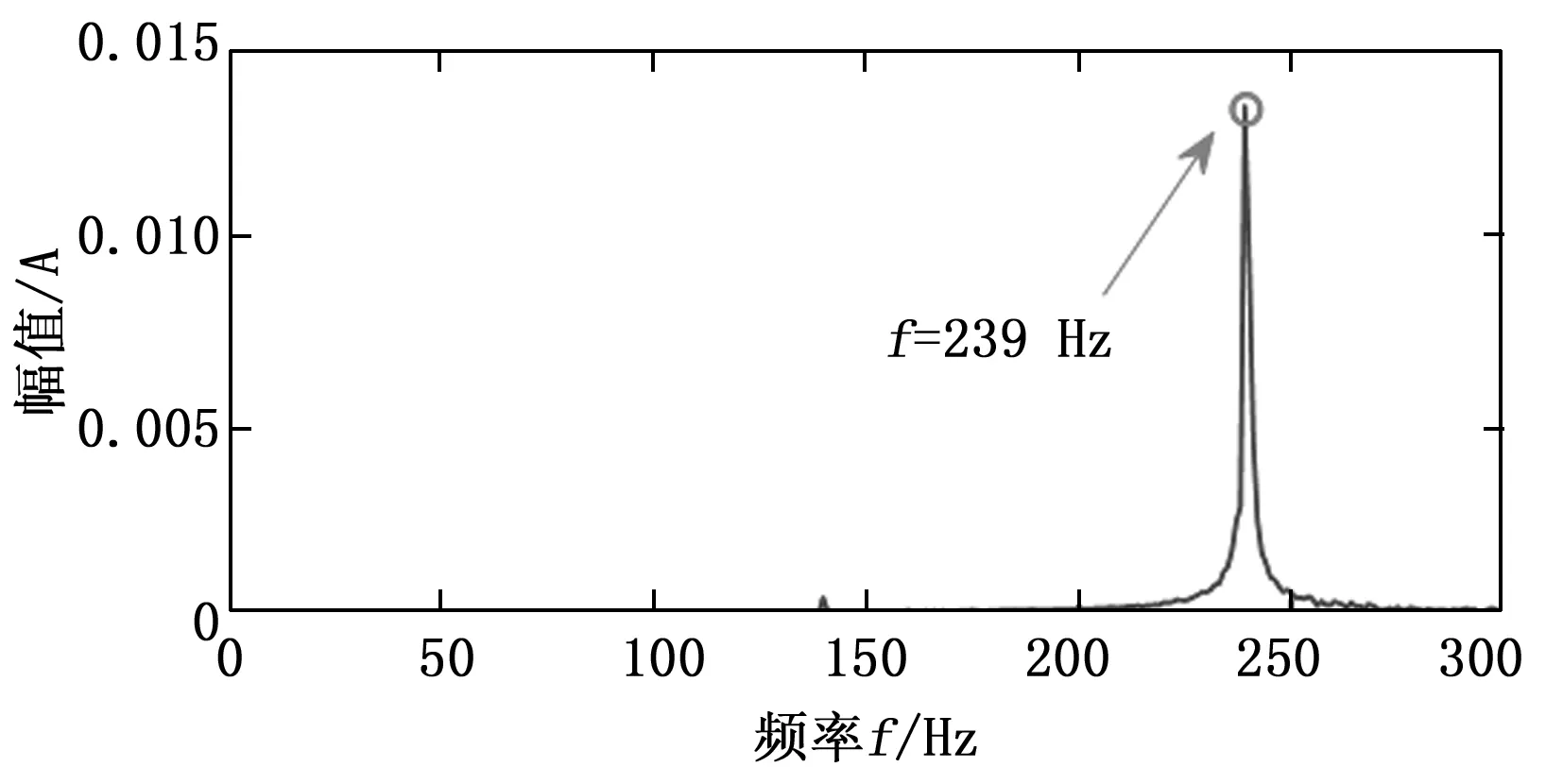
图15 突降前信号片段频谱图

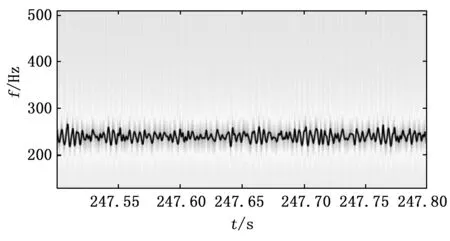
图16 突降前信号片段非线性压缩变换时频图

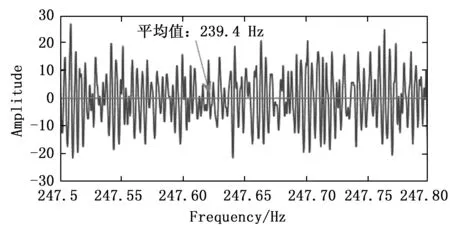
图17 高压转频附近脊线图

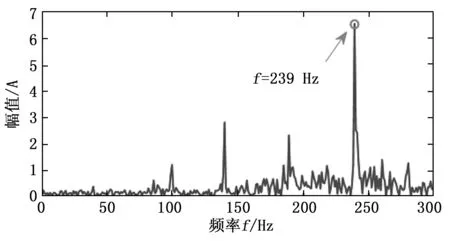
图18 高压转频附近脊线频谱图

上述振动信号分析结果表明：无论是振动幅值的突增还是突降，都是该试车发动机的高压转子工频成分在转频几乎不变的情况下振动幅值发生突变导致的。并且这种突变是可逆的，既可以增大也可以减小，突变在非常短的时间内完成，且在突变完成后该发动机又能继续在该状态稳定运行。航空发动机这种可逆的振动突变表明，发动机存在两个稳定的工作区域，即“双稳态”现象，这种“双稳态”之间的振动突跳是一种典型的非线性动力学行为。

根据航空发动机双转子系统的结构特点，可将引起非线性动力学问题的原因分为内部原因与外界原因两类：前者包括热弯曲、裂纹、不对中等转子自身故障；后者包括轴承失效、支撑松动或变形、挤压油膜阻尼器等支撑非线性因素，叶片碰摩之类的接触非线性因素以及喘振、封严系统气流激振等流-固耦合非线性因素。该航空发动机这种可逆的振幅突跳现象与上述的多种不可逆的非线性原因不符。例如，转子自身存在的故障往往是不可逆的，轴承失效故障也是不可逆的，因此可以首先排除这两类故障。挤压油膜阻尼器工作不正常导致的振动突跳不是同频突跳，而是从某个频率的振动运行状态突然变化至另一个频率的振动[18]。上述分析结果可以证明该发动机高压转子工频成分的突跳现象和挤压油膜阻尼器导致的非线性现象不符，所以该类故障也被排除。

此外，小状态突增后与大状态突降前的振动信号中以高压转频为基频，又以高压转频为调制频率的调频现象与转子碰摩导致的非线性现象非常相似，所以该振动信号的振幅突变现象可能是发动机转子碰摩所致[19-20]。但是，除了以上已经排除的故障之外，其他非线性因素并不能排除，所以，是否为转子碰摩导致的振动信号突变还需要进一步的分析与验证。

4 结束语

本文对某型航空发动机进行地面整机试车试验，并通过数据采集装置获取各测点的振动信号，然后利用非线性压缩变换良好的微弱特征表征能力与时频聚集性，并结合其他信号分析方法，对采集到的振动信号进行分析。最终，结合航空发动机的结构与理论知识，实现了对其可能存在故障的排查与猜测，同时验证了非线性压缩变换在航空发动机实际试车信号分析中的有效性与实用性。

然而，本文仅对该航空发动机可能存在的故障进行了猜测，也排除了一些不可能存在的故障，但是并不能准确分析出该航空发动机的具体故障模式，因此还需要开展进一步的试验进行分析验证。