西南地区水平向峰值速度、峰值位移衰减关系研究
张斌, 俞言祥 , 李小军, 王玉石, 荣棉水
1 北京工业大学城市建设学部, 北京 100124 2 中国地震局地球物理研究所, 北京 100081
0 引言
地震动衰减关系是确定工程结构抗震设防要求和设计地震动参数的关键环节,如编制地震动参数区划图、开展重大工程场地地震安全性评价等工作.PGV和PGD在地震工程中应用广泛.比如,PGV与埋地管道的地震破坏密切相关(O′Rourke et al.,2001).在一些方法中PGV被作为估计砂土液化潜在性的参数(Kostadinov and Towhata,2002;Orense,2005).PGV也被证明是一个可以用来判断地震动对中等周期结构造成破坏的可靠指标,与烈度和观测到的结构破坏都有很好的相关性(Wald et al.,1999;Kaka and Atkinson,2004).Akkar和Özen(2005)分析了几种多自由度抗震框架结构在中强震的强震动记录下的响应,证明PGV可以作为一种简单可靠的损伤可能性指标.近年来,我国特大新型建设工程、基础设施如高层和超高层建筑、大跨桥梁等长周期结构越来越多,而PGD类参数可以表征长周期结构的地震影响(陈波,2013).尽管PGV和PGD在地震工程中有广泛的应用,但是国内关于地震动PGV和PGD衰减关系的研究目前还很少.主要有两个方面的原因:其一是由于之前我国强震动台网密度较低,强震动数据缺乏,无法直接利用强震动数据进行统计回归.汪素云等(2000)考虑了震级和距离项,利用中线映射转换方法(胡聿贤等,1996)建立了我国分区的水平向基岩地震动PGV衰减关系.但是地震动衰减关系忽略场地的线性和非线性响应将增大地震动估计中的不确定性.另一个原因是PGV尤其是PGD对于高通滤波截止频率的选取非常敏感,没有合理可靠的数据处理方法获取大量的PGV和PGD数据.
国际上关于地震动PGV、PGD衰减关系研究已经考虑与地震动有关的多个因素的影响.如NGA-West1/2四个团队基于随机效应回归法或两步回归法(Abrahamson and Youngs,1992;Joyner and Boore,1993),相继统计回归获得包含震级项、距离项、上/下盘效应项、断层类型项、线性和非线性场地响应项、盆地效应项和区域差异性等影响因素的浅地壳活动构造区(主要是美国西部地区)的水平向地震动PGV衰减关系(Abrahamson and Silva, 2008; Abrahamson et al.,2014;Boore and Atkinson, 2008; Boore et al.,2014;Campbell and Bozorgnia, 2008,2014;Chiou and Youngs,2008,2014)和水平向地震动PGD衰减关系(Campbell and Bozorgnia,2008).NGA-West2衰减关系适用于震级M3.5~8.0,距离0~300km,涵盖了工程应用所需的震级-距离范围,可以很好地体现震源特性、传播介质、场地影响等多个与地震动有关的因素对地震动衰减特征的影响.然而,地震动衰减关系存在着区域性差异(Douglas,2004;Chiou et al.,2010;Mahani and Atkinson,2013;Kale et al.,2015).比如,NGA-West1/2衰减关系高估了西南地区汶川、芦山和鲁甸地震的中长周期地震动(Wang et al.,2010;Xu et al.,2015;冀昆等,2016;张斌等,2020a).同时,Campbell和Bozorgnia(2008)是将直接估计参数Sa(T=10.0 s)来代替估算PGD,这是直接估计参数的不良替代,有较大的不确定性.因此,只有利用本地区的强震动数据进行统计回归得到的地震动衰减关系才能更真实地反映该地区地震动的衰减特性.
我国西南地区地震活动强烈,大震和强震如汶川、芦山、九寨沟和鲁甸地震等频繁发生,对中、长周期结构重大工程造成严重破坏.为此,迫切需要对我国西南地区的地震动PGV、PGD衰减特性开展系统深入研究,建立更加合理可靠的地震动PGV、PGD衰减关系.2008年以来西南地区布设密度越来越大的强震动台网记录到大量高质量的强震动记录,国际上对地震动衰减模型和回归方法的研究和认识不断深入和进步,以及西南地区大量中、长周期结构重大工程建设的抗震设防需求、设计地震动参数对于更精确PGV、PGD估计结果的迫切需求.在此背景下,本文开展了西南地区水平向地震动PGV、PGD衰减关系研究.基于西南地区大量的高质量强震动数据,利用合理可靠的强震动数据处理方法获得大量PGV、PGD数据,建立包含震级和距离饱和效应、震级相关几何衰减、线性/非线性场地响应、非弹性衰减以及事件间和事件内变化性的衰减模型,利用随机效应回归法统计得到西南地区考虑多个影响因素的水平向PGV、PGD衰减关系.可以为西南地区确定中、长周期结构重大工程的抗震设防需求、设计地震动参数提供更精确的结果.同时也为我国西南地区建立多影响因素的水平向峰值加速度、加速度反应谱衰减关系研究进行前期探索.
1 强震动数据集
1.1 强震动数据选取和处理
本文研究的西南地区水平向PGV、PGD衰减关系主要是针对西南地区4.0
经过上述筛选后的记录,对于大震近断层强震动记录的基线误差,采用了基线校正的改进方法(张斌等,2020b)进行处理.该方法利用时移斜率比、位移时程平坦度和均方根偏差等判定标准确定强震段瞬时偏移开始时间点t1、结束段永久偏移开始时间点t2和位移末尾部分拟合函数的次数.并将获得的永久位移与强震动台站附近的GPS台站观测的同震位移进行对比验证了该方法的合理可靠性.我们认为利用该基线校正改进方法处理本文选取的大震近场强震动记录可以获得加速度记录对应的较可靠的PGV和PGD值.其余的强震动记录采用了NGA-West2数据处理流程(Ancheta et al.,2014),应用4阶非因果Butterworth带通滤波进行处理,低通截止频率为30 Hz.为了保证确定的滤波高通截止频率的有效性和尽量减小滤波对PGD的影响,首先根据震源谱模型的理论频率、加速度的傅里叶振幅谱在低频段的衰减正比于f2,噪声的出现会造成傅里叶振幅谱在低频段的翘起(Joyner and Boore,1988;Atkinson and Silva,2000)以及记录的信噪比不小于3(Boore and Bommer,2005)等判定标准确定高通截止频率的范围.然后在该范围内以0.01 Hz的间隔逐一选取高通截止频率进行处理,最后根据处理后的速度和位移时程的末尾是否在零线确定最终的高通滤波截止频率,获得PGV和PGD.每条记录都经过作者重复校对、检查.
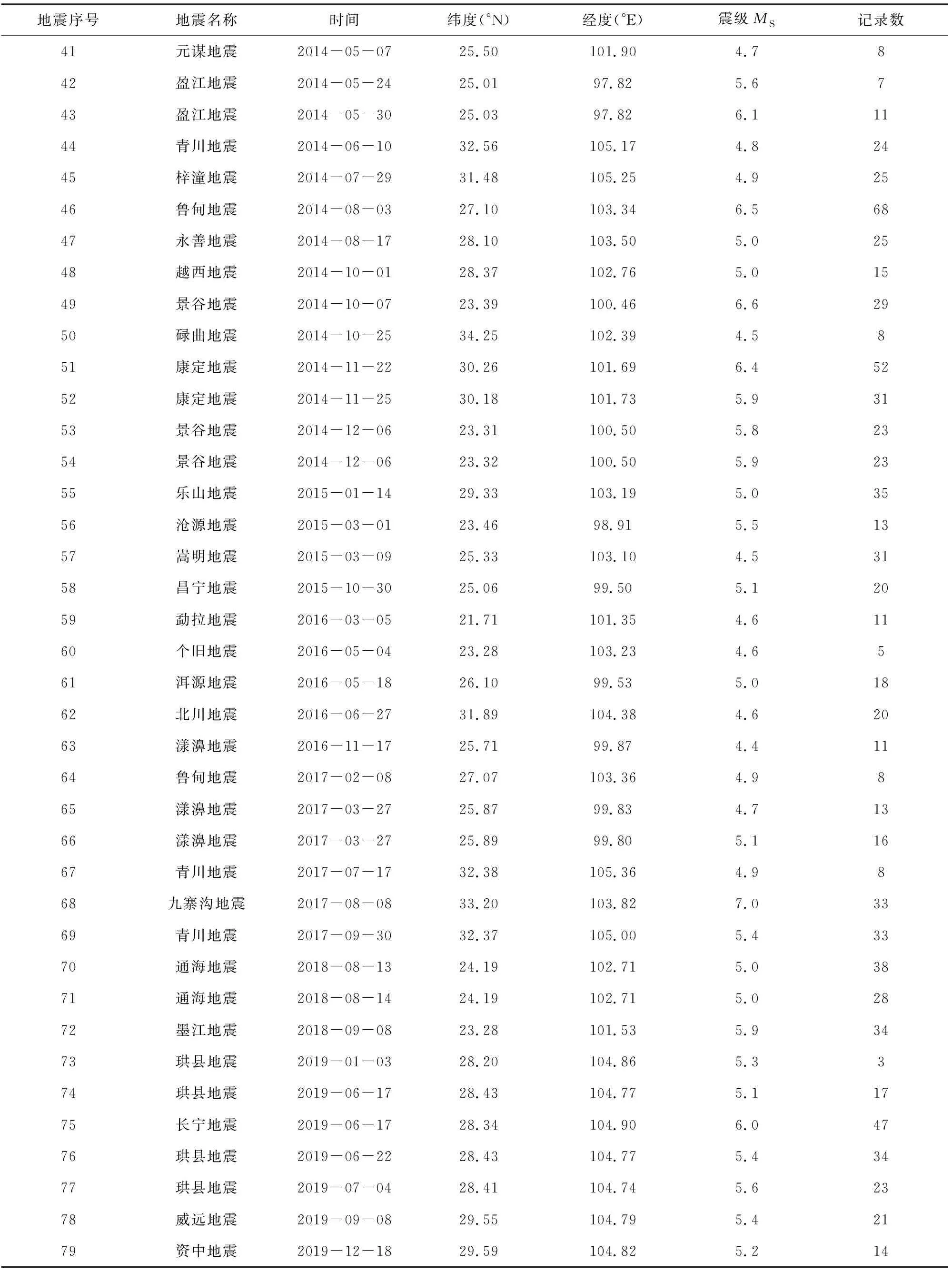
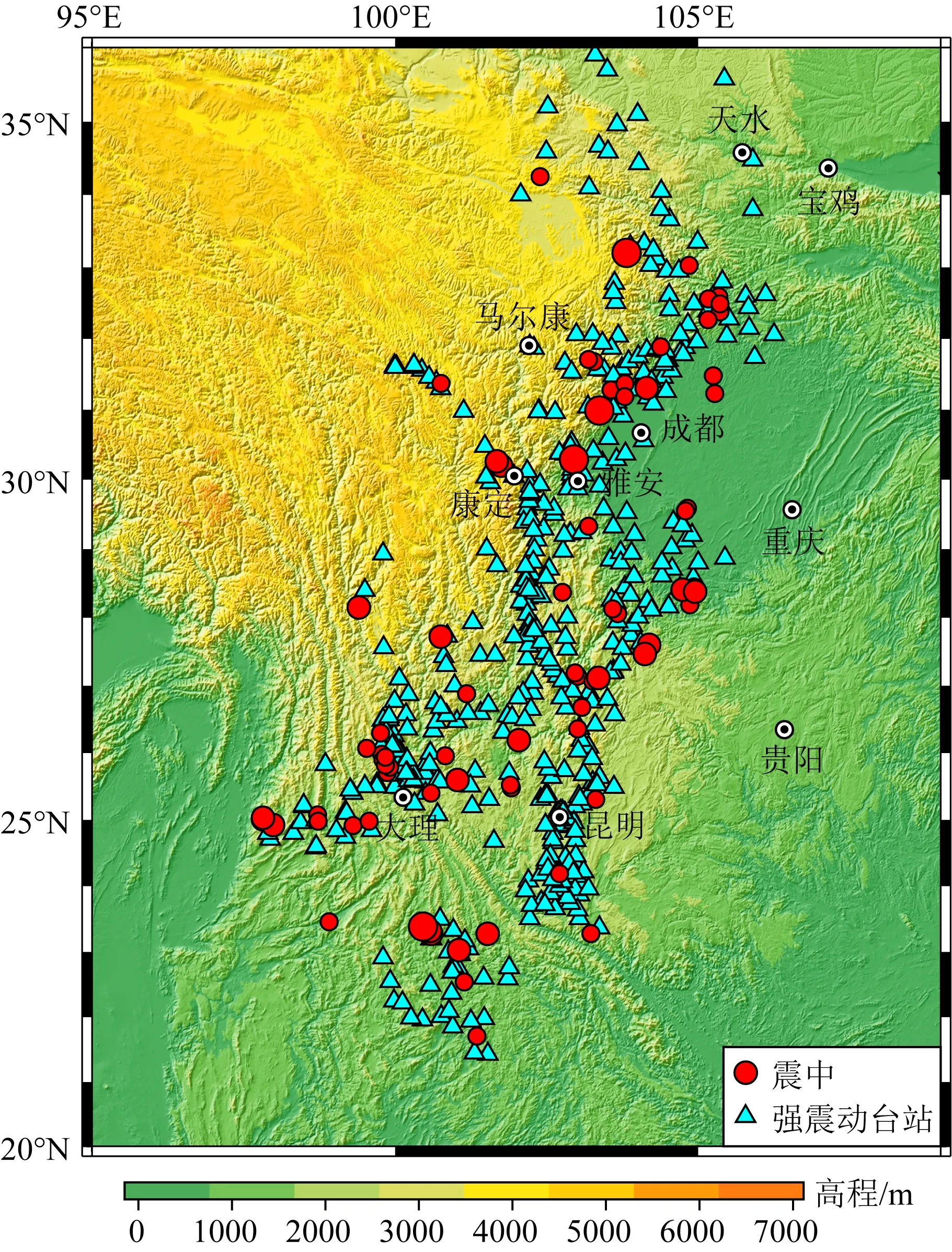
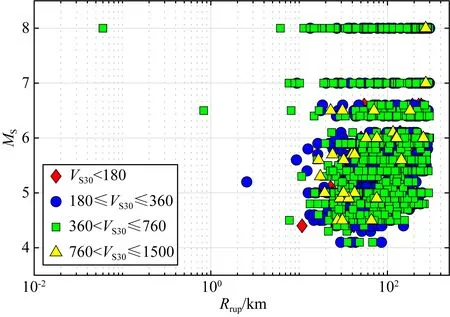
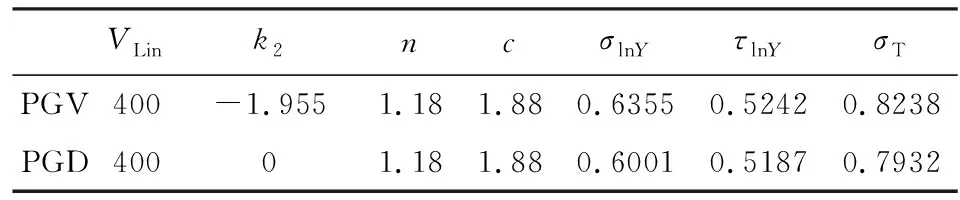
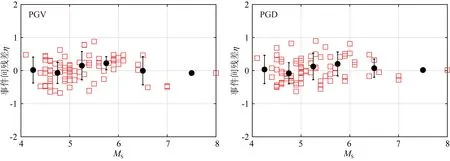
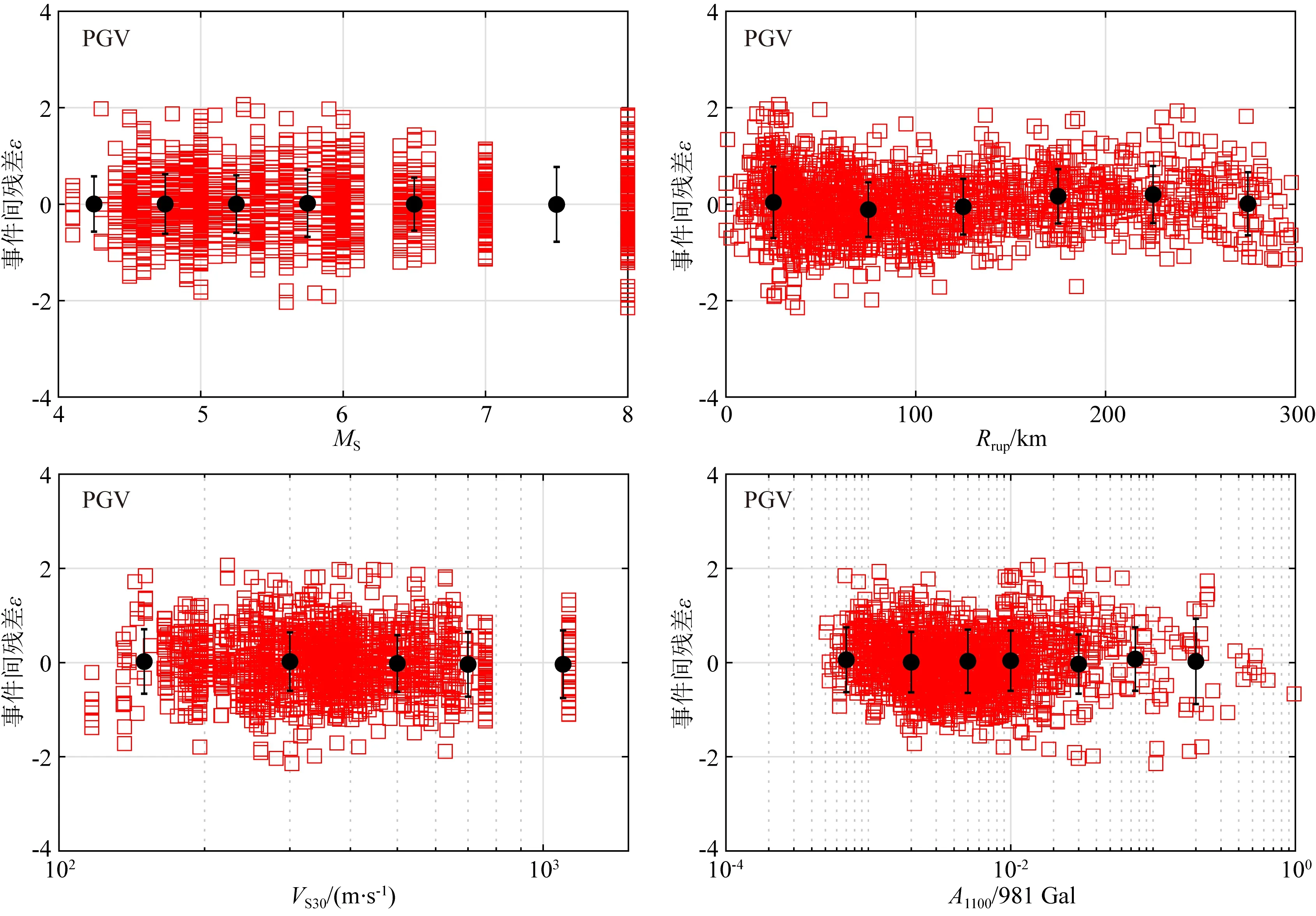
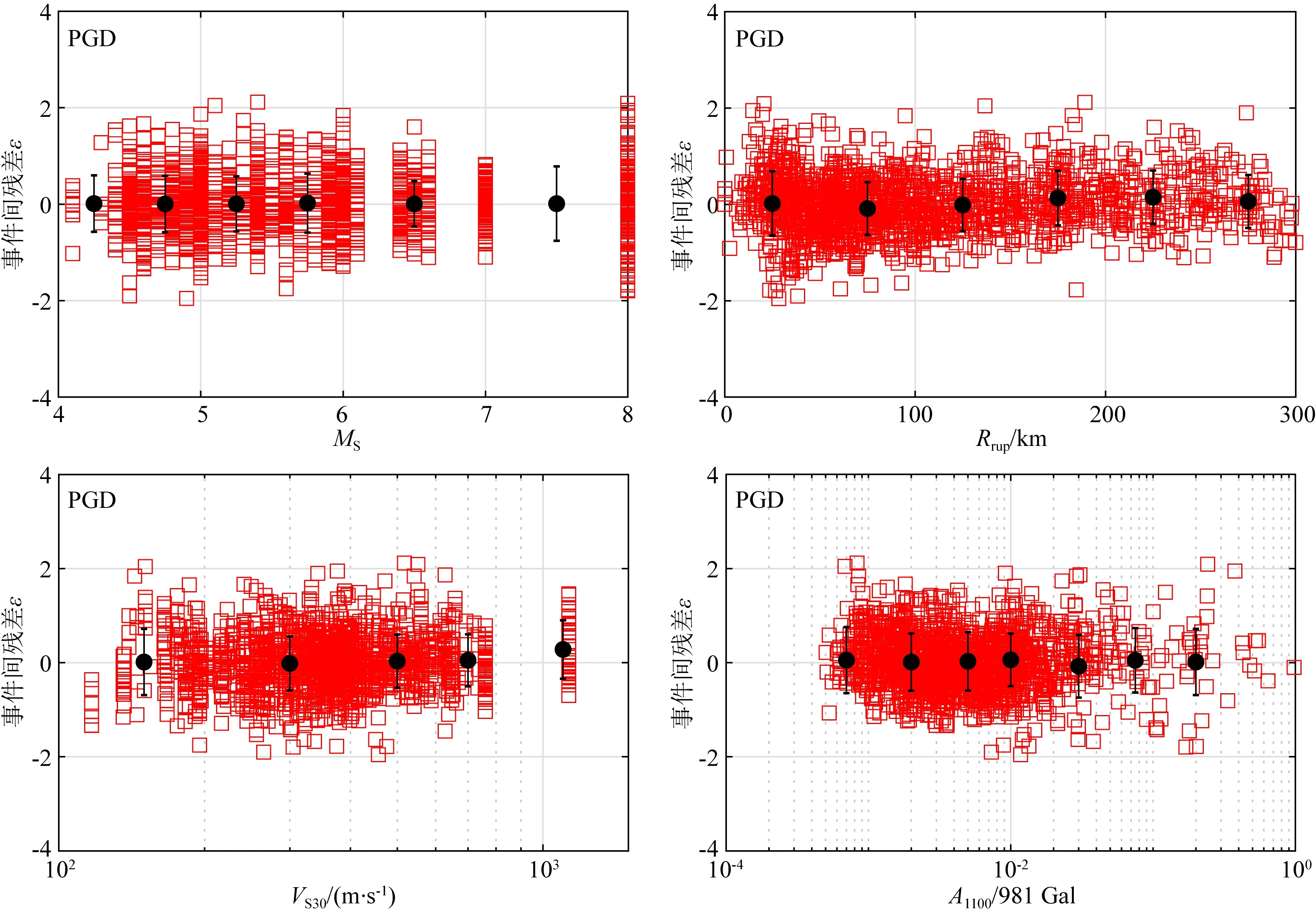
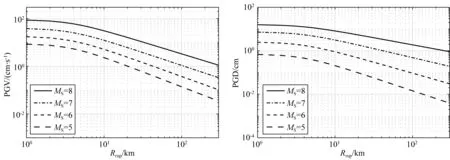
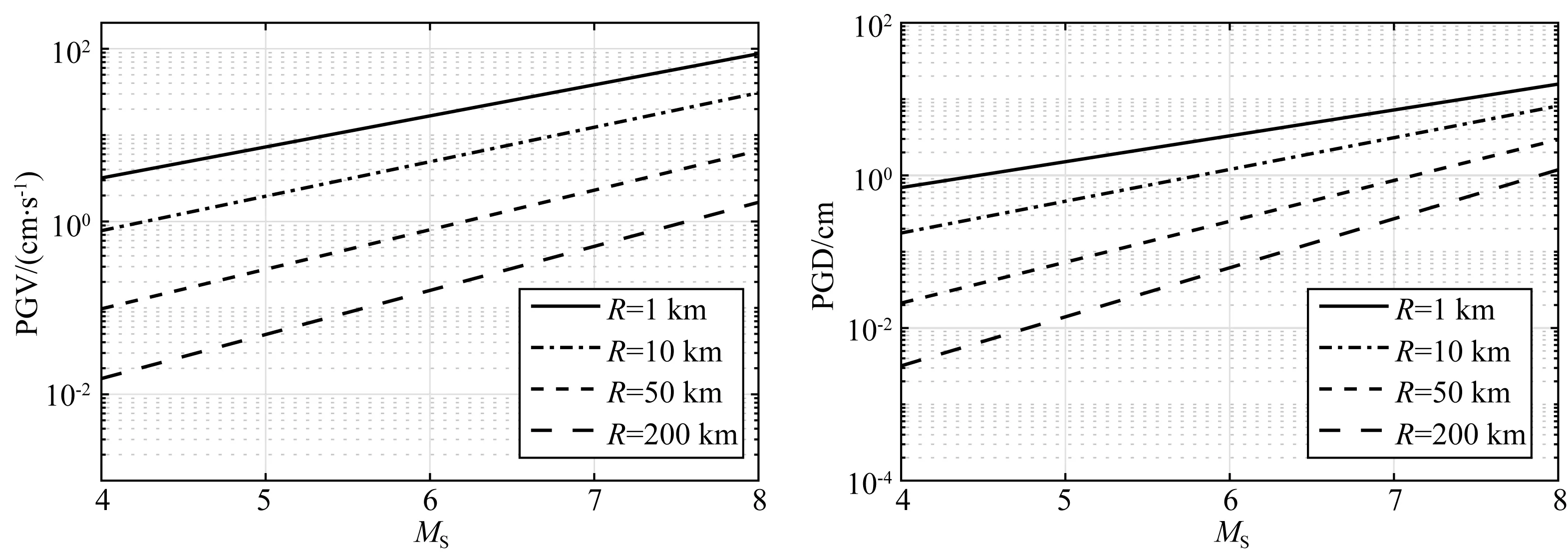
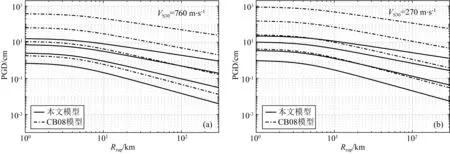
Campbell和Bozorgnia(2007)分析结果表明,地震动PGV和PGD两个水平分量的几何均值和NGA-West1衰减关系中采用的方向无关的GMRotI50值比值的均值分别为0.988、0.981,两者非常接近.因此,本文选取同一个台站两个水平分量的PGV和PGD几何均值作为回归数据.应用上述数据筛选标准,最终的数据集包含西南地区79个4.0 表1 本文中使用的西南地区地震和记录目录Table 1 Catalog of earthquakes and records in southwest China used in this study 续表1 图1 选取的79个4.0 图2 本研究中选取的不同场地类别强震动数据的震级-距离分布图Fig.2 Magnitude verse distance scatters for site class of strong motion data used in this study 在本文衰减模型中,使用的距离参数为断层距(Rrup).根据Kaklamanos等(2011)方法确定断层距,首先必须获取地震的有限断层模型.大震和强震的有限断层模型有学者进行专门的研究并公布.不同学者给出的有限断层模型会因为采用的反演方法或数据资料不同会有较小的差别,但对于距离参数的计算结果影响不大.本文中汶川、芦山、鲁甸、康定双震和九寨沟等6个地震的有限断层模型选取了根据远震体波、近震宽频带、强震动资料、基阶Love波视震源时间函数和InSAR资料联合反演得到的结果(张勇等,2008,2015;张旭, 2016; 张旭等,2017). 张斌(2019)详细介绍了断层距的具体计算过程.而我国4.0 本文中使用的西南地区493个强震动台站的场地VS30主要来源于:(1)喻畑和李小军(2015)给出的四川和甘肃强震动台站的场地VS30;(2)收集了四川103个和云南159个强震动台站的钻孔资料,分别采用速度梯度线性模型(喻畑和李小军,2015;Boore,2004)延拓得到的场地VS30;(3)NGA-West2 Flatfile公布的汶川地震强震动台站的场地VS30;(4)没有钻孔剪切波速资料而有钻孔岩性编录的台站,根据NEHRP场地分类E、DE、D、CD、C、BC、B分别给出场地VS30值150、180、255、360、525、760和1070 m·s-1(Campbell and Bozorgnia,2007);(5)既没有钻孔波速测试资料也没有钻孔岩性编录的台站,根据Allen和Wald(2009)提出的地形坡度与VS30的修正关系得出场地VS30. 本文采用的经验地震动衰减模型的函数形式为 (1) 采用了震级相关的距离项来体现大震近场距离饱和效应: (2) 震级项采用分段线性函数(Campbell and Bozorgnia,2008)来表示,如式(3).既可以很好的体现震级饱和效应,又可以将大震、中震和小震的衰减分离,从而可以更灵活的体现地震动PGV、PGD随MS的衰减规律. (3) 软土场地的非线性特性非常复杂,目前还没有足够的经验数据对其进行有效约束.场地项采用了线性场地响应和Walling等(2008)基于一维等效线性场地反应开发的非线性场地响应模型来表示(Campbell and Bozorgnia,2008): (4) 参考场地的VS30=V1=1100 m·s-1,fsite=0,V1是Campbell和Bozorgnia(2008)在残差分析后施加的该约束,防止模型低估长周期和较大的VS30值时的地震动.A1100是参考场地的峰值加速度(PGA)输入.场地非线性会随着场地VS30越小(VS30 地震动的非弹性衰减在Rrup>80 km时具有很强的区域差异性,与地壳品质因子呈e-γr的衰减,γ是该地区的地壳品质因子,r是距离,而近源(Rrup≤80 km)的地震动参数则没有表现出明显的非弹性衰减效应(Campbell and Bozorgnia,2013).同时,在工程应用和地震危险性分析中近源距离的地震动参数非常重要.因此,本文将近源和中、远源数据的分界距离选为80km.针对MS>6.5、Rrup>80 km的记录,在衰减模型中考虑非弹性衰减项,如式(5): (5) 先拟合出所有其他项的系数,然后保持这些系数不变,使用远场(80 本文使用了随机效应回归法(Abrahamson and Youngs,1992)来获得经验地震动衰减关系,为了与随机效应回归分析相一致,利用式(6)定义随机不确定性模型: (6) 其中,ηi是事件i的事件间残差,Yij、εij分别是事件i记录j的地震动PGV、PGD的实际观测值和事件内残差.事件间残差表示一次地震与所有地震平均水平的差异.事件内残差表示某一记录与此次地震所引起的地震动平均水平的差异.独立正态分布变量ηi、εij的均值为零,标准差分别为τ和σ.总的标准差由式(7)确定: (7) 总残差rij由实际观测值减去估计值获得,与事件间和事件内残差ηi、εij相关联,如式(8): (8) 事件间和事件内残差ηi、εij由式(9、10)确定: (9) εij=rij-ηi, (10) 利用随机效应回归法获得西南地区水平向PGV和PGD衰减模型的系数c0~c8列于表2.表3给出了周期相关的模型系数VLin、k2,周期无关的模型系数c=1.88、n=1.18以及随机不确定模型的事件间残差、事件内残差和总残差的标准差. 表2 西南地区水平向PGV、PGD衰减模型系数Table 2 Coefficients for the horizontal PGV and PGD attenuation model in southwest China 表3 周期相关、周期无关的模型系数和随机不确定性模型的标准差Table 3 Coefficients for period-dependent, -independent model and standard deviations for the aleatory uncertainty model 为了评估本文获得的西南地区水平向PGV、PGD衰减关系的有效性,绘制了事件间和事件内残差相对模型中各个预测变量的变化图,如图3—5.图中残差正值表示本文衰减关系低估了观测值,残差负值表示本文衰减关系高估了观测值.图3给出了PGV、PGD事件间残差随MS的分布.由图3可知,PGV和PGD的事件间残差均匀分布在-1~1之间,且在每个MS区间内的事件间残差均值均位于零值附近,未表现出系统的趋势或偏差.表明本文模型对PGV和PGD的估计相对于MS相对无偏差,观测值与估计值相差无几,结果是可靠的.图4和5给出了PGV、PGD的事件内残差随MS、Rrup、VS30和A1100的分布.由图4和5可知,PGV、PGD的事件内残差随MS、Rrup、VS30和A1100的变化均匀分布在-2~2之间,在各个MS、Rrup、VS30、A1100区间内的事件内残差均值都分布在零值附近,表明本文模型对PGV、PGD的估计相对于MS、Rrup、VS30、A1100相对无偏差. 图3 PGV、PGD的事件间残差(η)随震级MS的分布黑色实心点和误差棒分别表示各个MS区间事件间残差的均值和95%置信区间Fig.3 Distribution of inter-event residuals (η) with respect to surface magnitude (MS) for PGV and PGDBlack circles and Error bars represent the mean and 95th-percentile confidence limits of inter-event residuals in every MS bin. 图4 PGV的事件内残差(ε)随MS、Rrup、VS30、A1100的分布黑色实心点和误差棒分别表示各个MS、Rrup、VS30、A1100区间事件内残差的均值和95%置信区间.Fig.4 Distribution of intra-event residuals (ε) with respect toMS,Rrup,VS30,A1100 for PGVBlack circles and Error bars represent the mean and 95th-percentile confidence limits of intra-event residuals in every MS,Rrup,VS30,A1100 bin. 图5 PGD的事件内残差(ε)随MS、Rrup、VS30、A1100的分布黑色实心点和误差棒分别表示各个MS、Rrup、VS30、A1100区间事件内残差的均值和95%置信区间.Fig.5 Distribution of intra-event residuals (ε) with respect toMS,Rrup,VS30,A1100 for PGDBlack circles and Error bars represent the mean and 95th-percentile confidence limits of intra-event residuals in everyMS,Rrup,VS30,A1100 bin. 为了评估本文水平向PGV、PGD衰减关系的有效性,图6和图7分别给出了在基岩场地(VS30=760 m·s-1)时本文模型的地震动PGV、PGD估计值随Rrup、MS的变化曲线.图6中四条曲线分别代表本文模型在MS=5、6、7、8的衰减特征.由图6可知,本文模型显示了震级相关的地震动PGV、PGD随距离的衰减,表现出大震近场震级饱和效应.由于在Rrup<10 km的数据极少,该距离范围内的衰减曲线通过10≤Rrup<300 km的数据外推获得.在Rrup<10 km距离范围,四个震级的PGV、PGD衰减曲线的斜率大体相同.在10≤Rrup<300 km距离范围,距离越远PGV的衰减比PGD更快.图7中四条曲线分别代表本文模型在Rrup=1、10、50、200 km时PGV和PGD估计值随MS的变化关系.从图7也可以看出本文模型表现出PGV和PGD的震级饱和效应,即随着震级的增大和距离的减小,PGV和PGD的增大放缓,没有出现过饱和现象. 图6 西南地区水平向PGV、PGD与震级相关的随Rrup变化的衰减曲线对地震动衰减模型在MS=5、6、7、8,VS30=760 m·s-1进行评估.Fig.6 Attenuation curves of horizontal PGV and PGD with Rrup showing its dependence on MS in southwest ChinaThe ground motion attenuation model is evaluated for MS=5,6,7,8, VS30=760 m·s-1. 图7 西南地区水平向PGV、PGD与距离相关的随震级MS的变化关系对地震动衰减模型在Rrup=1、10、50、200 km,VS30=760 m·s-1进行评估.Fig.7 Scaling of horizontal PGV and PGD with MS showing its dependence on rupture distance (Rrup) in southwest ChinaThe ground motion attenuation model is evaluated forRrup=1, 10, 50, 200 km, VS30=760 m·s-1. 图8显示了本文模型估计的PGV、PGD场地放大与基岩上PGA(A1100)的相关关系.由图可知,对于PGV,VS30=150、255 m·s-1的场地放大随着A1100的增大而减小,而VS30=525、1070 m·s-1的场地放大无明显变化.当A1100<98.1 Gal时,VS30越大PGV的场地放大越小;A1100>98.1 Gal时,VS30越大PGV的场地放大越大.对于PGD,随着A1100的增大,不同VS30对应的场地放大均无变化,fsite(VS30=150 m·s-1)>fsite(VS30=255 m·s-1)>fsite(VS30=525 m·s-1)>fsite(VS30=1070 m·s-1).这表明本文使用的非线性场地响应模型(Walling et al.,2008)可以结合经验地震动衰减模型更好的捕获土层非线性的平均效应. 图8 场地放大与A1100之间的相关关系针对VS30=1070 m·s-1(NEHRP B)、VS30=525 m·s-1(NEHRP C)、VS30=255 m·s-1(NEHRP D)和VS30=150 m·s-1(NEHRP E)评估场地放大.Fig.8 Correlation of site amplification with rock PGA (A1100) showing its dependence on 30-m shear-wave velocity (VS30)The aleatory uncertainty model is evaluated for VS30=1070 m·s-1(NEHRP B), VS30=525 m·s-1(NEHRP C), VS30=255 m·s-1(NEHRP D) and VS30=150 m·s-1(NEHRP E). 将汶川、芦山、鲁甸、九寨沟四个大震和强震的水平地震动PGV、PGD的观测值与本文衰减曲线相对于Rrup的变化进行对比(图9—10),VS30分别取四个地震的强震动台站场地VS30的中位数382.83、392.30、351.35、371.40 m·s-1.四个地震的有限断层模型与前文分析中选用的相同.图9和10中的黑色实线是衰减曲线,黑色虚线表示估计值的±1倍标准差值.由图可知,绝大多数的汶川、芦山、鲁甸、九寨沟地震的水平向PGV、PGD观测值在整个距离范围内都位于本文PGV、PGD衰减曲线的±1倍标准差以内,只有少数汶川地震200 图9 本文模型的汶川、芦山、鲁甸、九寨沟地震PGV衰减曲线(VS30分别为382.83、392.30、351.35、371.40 m·s-1)分别与观测值的对比Fig.9 Comparison of estimates of PGV from our model (VS30is 382.83, 392.30, 351.35 and 371.40 m·s-1, respectively) with the corresponding observed values at the stations of the Wenchuan, Lushan, Ludian, and Jiuzhaigou earthquakes, respectively 图10 本文模型的汶川、芦山、鲁甸、九寨沟地震PGD衰减曲线(VS30分别为382.83、392.30、351.35、371.40 m·s-1)分别与观测值的对比Fig.10 Comparison of estimates of PGD from our model (VS30is 382.83, 392.30, 351.35 and 371.40 m·s-1, respectively) with the corresponding observed values at the stations of the Wenchuan, Lushan, Ludian, and Jiuzhaigou earthquakes, respectively 肖亮(2012)基于美国西部水平向基岩地震动衰减关系和我国分区的烈度衰减关系,采用中线映射转换方法建立了我国分区的水平向基岩地震动衰减关系.我国第五代地震动参数区划图采用了该地震动衰减关系,其包含了川藏区的地震动PGV衰减关系(长、短轴模型).将本文结果与川藏区地震动PGV长、短轴衰减关系进行对比,并增加了基岩场地的观测数据.由于肖亮(2012)川藏区PGV衰减关系是针对基岩场地开发的,我国抗震设计规范中规定VS20>500 m·s-1的场地为基岩.因此,用于对比的观测数据为VS20>500 m·s-1场地的数据,本文衰减关系选用的场地VS30为选用观测数据的场地VS30中值643.32 m·s-1.距离采用了断层距.对比结果如图11所示.从图中可知,本文地震动PGV衰减曲线很好的拟合了西南地区不同震级不同距离范围内基岩场地的数据,肖亮(2012)的结果在四个震级不同距离范围内大于绝大部分的基岩场地数据,表明川藏区PGV衰减关系在四个震级、0~300 km距离范围整体上估计偏高. 图11 本文模型和川藏区(a)长轴、(b)短轴在MS=5、6、7、8的PGV衰减曲线与基岩场地观测数据的对比Fig.11 Comparison of estimates of PGV from our model and Sichuan-Xizang model with observed values on rock site(The comparison is evaluated for MS=5,6,7,8) 将本文所得PGD衰减关系计算结果与Campbell和Bozorgnia(2008)结果分别在基岩(VS30=760 m·s-1)和土层(VS30=270 m·s-1)场地进行对比.对模型在MS=5、6、7、8、走滑断层(δ=90°)、ZTOR=1.0 km进行评估,如图12所示.结果表明,无论是基岩场地还是土层场地,本文衰减关系与CB08模型在MS=5、6、7、8的PGD衰减曲线有较大的差异,CB08模型在整个距离范围内的估计值远大于本文模型,尤其是MS=7、8.这与NGA-West1模型高估了西南地区汶川地震、芦山地震产生的长周期地震动(Wang et al.,2010;冀昆等,2016)的结果相符合. 图12 本文模型与CB08模型的PGD随断层距Rrup衰减的对比对模型在MS=5、6、7、8,走滑断层(δ=90°),ZTOR=1 km,(a)VS30=760 m·s-1、(b)VS30=270 m·s-1进行评估.Fig.12 Comparison of attenuation curves of PGD between our model and CB08 model with RrupThe comparison is evaluated for MS=5,6,7,8, Strike-slip (δ=90°), ZTOR=1 km, VS30=760 m·s-1 and VS30=270 m·s-1 本文利用合理可靠的数据处理方法获得西南地区水平向地震动PGV、PGD几何均值及相应的震源、距离和场地参数,统计回归得到西南地区水平向PGV、PGD衰减关系.本文衰减关系的PGV、PGD事件内和事件间残差在较小的范围内分布且没有系统的趋势和偏差以及西南地区汶川、芦山、鲁甸和九寨沟地震的绝大多数PGV、PGD观测值分布在本文PGV、PGD衰减曲线±1倍标准差以内表明本文水平向PGV、PGD衰减关系是可靠的. 对于PGD和A1100<98.1 Gal的PGV,场地放大会随着VS30的减小而增大,而A1100>98.1 Gal的PGV,场地放大会随着VS30的减小而越小.这与Walling等(2008)基于一维等效线性场地反应开发的非线性场地响应模型完全吻合,能很好的捕获土层非线性的平均放大效应(Campbell and Bozorgnia,2008).我们发现汶川地震少数远场台站的PGV、PGD观测值大于本文模型估计值.经研究发现,这些台站位于关中地区的宝鸡市,该地区地表覆盖的厚沉积层对远场的长周期地震动会有放大作用,导致这些台站的PGV、PGD被低估.在今后的地震动衰减关系研究中,对于远场存在覆盖厚沉积层的情况,需考虑厚沉积层对中长周期地震动的放大效应影响.区域大尺度盆地对地震动的长周期成分(PGV、尤其是PGD)的影响很显著(Bindi et al.,2009).然而,本文所选用的79个地震中只有四个中小震(2013年三台MS4.7地震、2014年梓潼MS4.9地震、2019年MS5.4威远和资中MS5.2地震)发生于四川盆地内部.所选的记录台站也只有23个位于四川盆地内部(总共493个台站).四川盆地对这些中小震和台站的强震动记录长周期成分的放大有限,对最终统计回归得到的西南地区水平向PGV、PGD衰减关系的整体趋势影响也有限.同时,本文衰减模型的场地项中考虑了土层的非线性放大作用,也能包含一部分盆地放大作用的影响.因此,本文衰减模型中没有再单独去考虑盆地项. 基于美国西部水平向基岩地震动衰减关系和我国分区的烈度衰减关系,采用转换方法建立的川藏区水平向基岩PGV衰减关系在四个震级、0~300 km距离范围内会轻微高估了西南地区基岩场地的PGV.CB08模型在四个震级、0~300 km距离范围内的PGD估计值远大于本文结果.本文PGV、PGD衰减曲线在大震近场表现出了震级饱和效应,相对于地震动高频分量,地震动PGV、PGD在大震近场的震级饱和效应并不明显.可能有以下两个方面的原因造成上述情况:一是CB08模型将直接估计参数Sa(T=10.0 s)来代替估算PGD,一般情况下会高估PGD;二是美国西部地区和集集地震的地震动长周期成分丰富(Loh et al.,2000)、而汶川、芦山地震的地震动长周期成分较弱(谢俊举等,2010;Xie et al.,2014).汶川、芦山地震的地震动长周期成分(PGD)异常低也可能造成出现假的震级饱和情况.目前还没有相关的研究成果证明汶川、芦山地震的长周期地震动异常低是单个地震的个体差异、或是大震发生的龙门山断裂带的普遍现象还是西南地区的区域特性,还需要在未来进行进一步研究. 我们认为在估算西南地区(1)4.0 致谢感谢中国地震局工程力学研究所“国家强震动台网中心”为本研究提供数据支持.感谢喻畑副研究员对本文回归方法的帮助.感谢PEER NGA提供汶川地震区强震动台站场地VS30数据.两位审稿专家对本文的完善提出了非常宝贵的意见,在此一并表示感谢.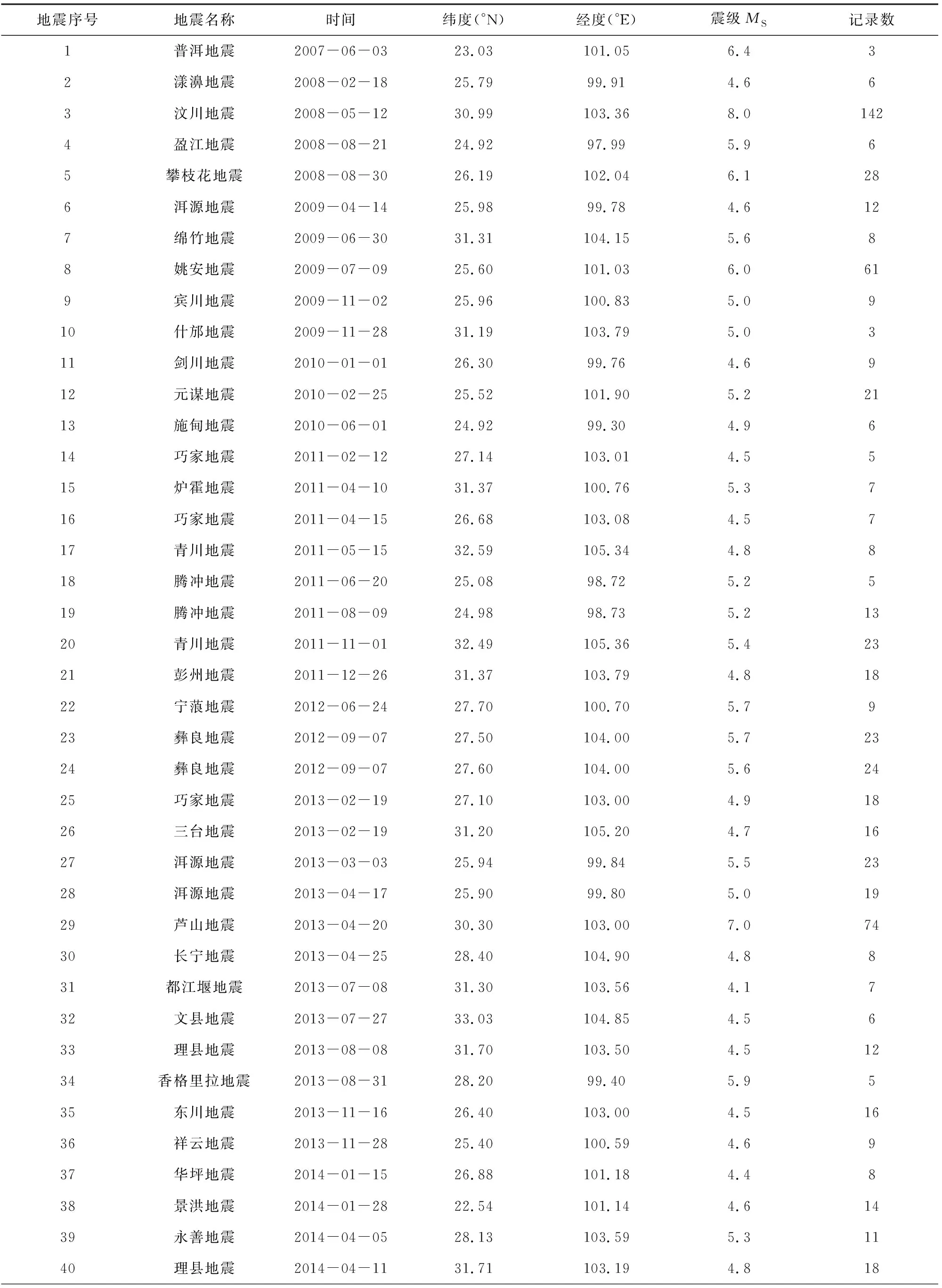
1.2 震源参数和距离参数
1.3 场地资料
2 地震动衰减模型
2.1 经验地震动衰减模型
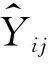
2.2 随机不确定性模型
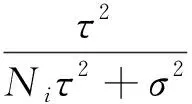
3 模型回归结果

3.1 残差评估
3.2 模型评估
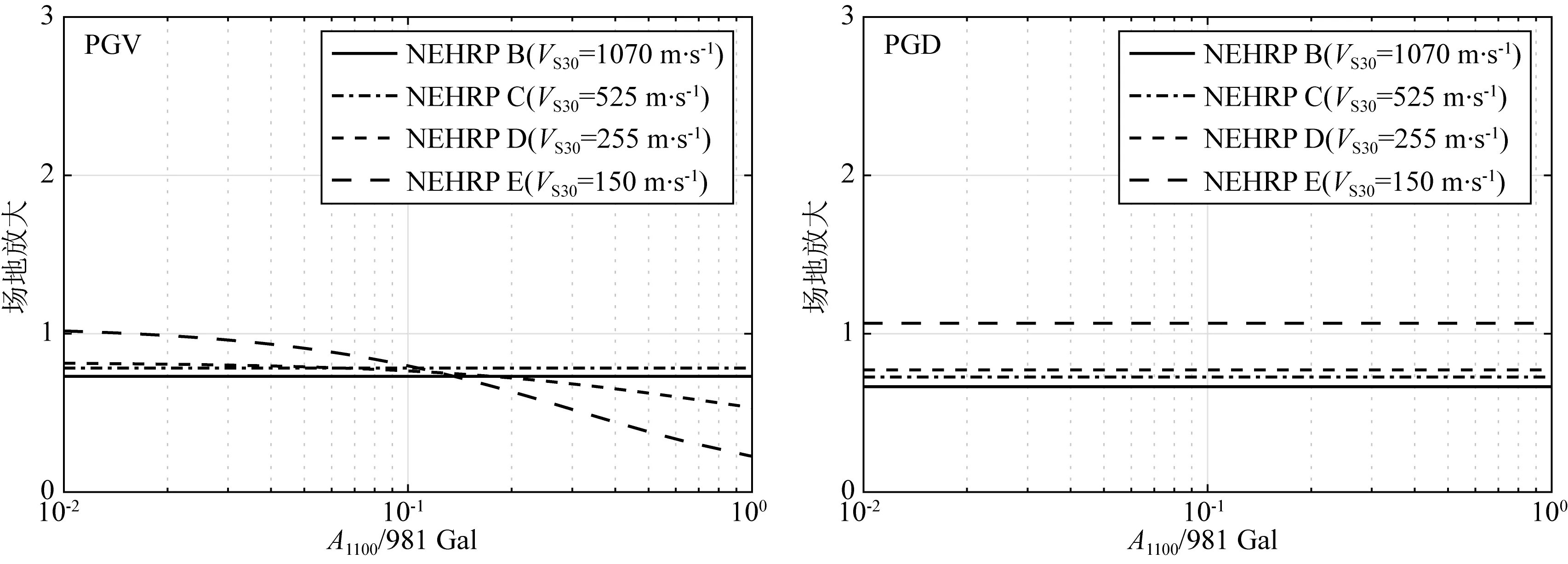
4 可靠性分析
4.1 本文衰减关系在汶川、芦山、鲁甸、九寨沟地震的衰减曲线与其强震动观测值的对比
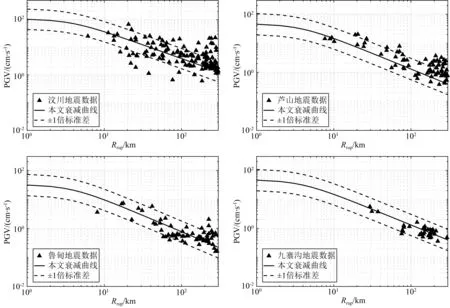
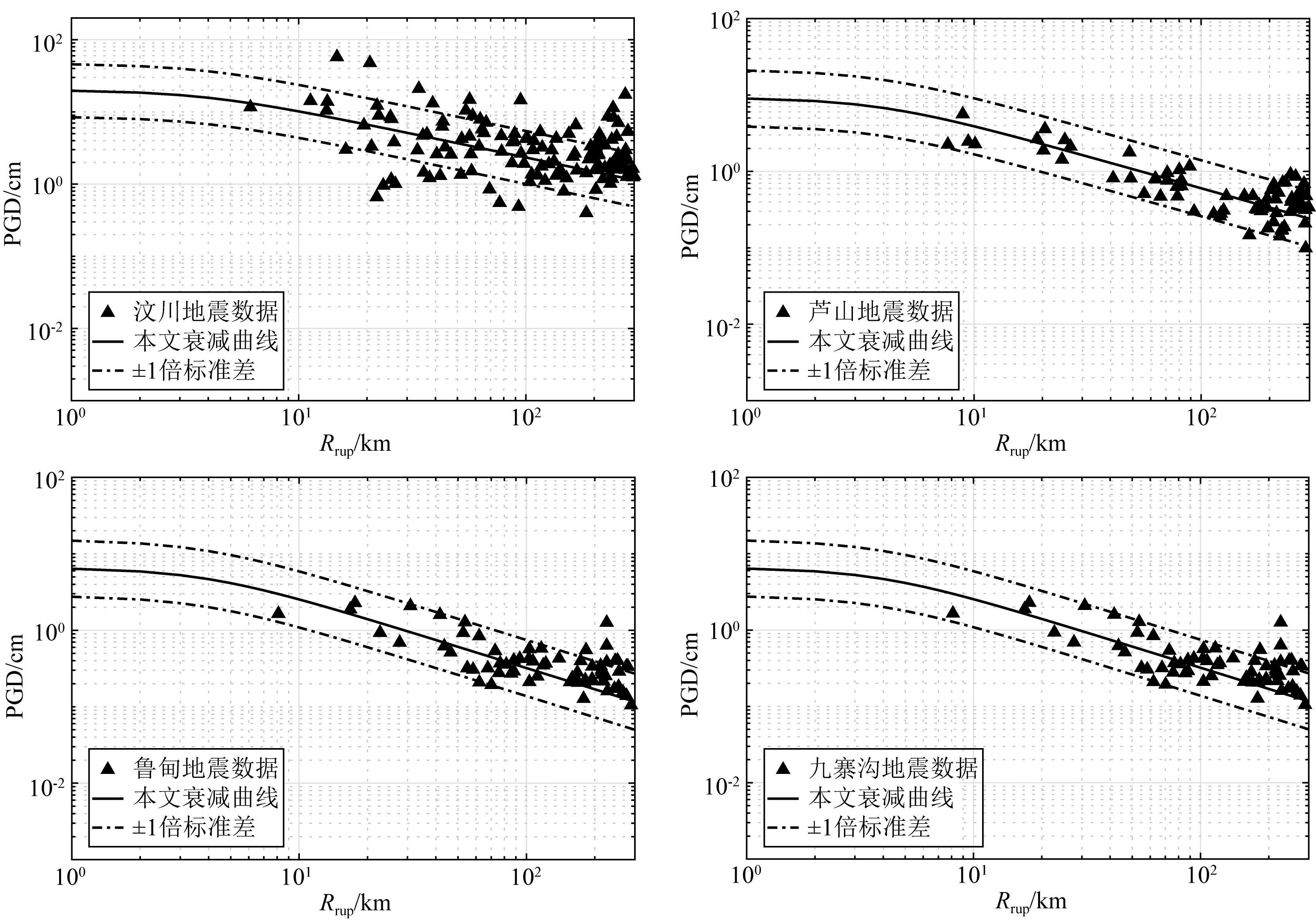
4.2 与国内常用衰减关系的对比
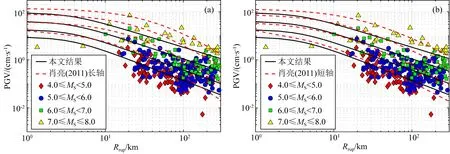
4.3 与Campbell和Bozorgnia(2008)模型的对比
5 结论与讨论
--западе Китая

