基于Levene检验的航空交流串联电弧故障检测

崔芮华 佟德栓

（1.省部共建电工装备可靠性与智能化国家重点实验室（河北工业大学） 天津 300130 2.河北工业大学河北省电磁场与电器可靠性重点实验室 天津 300130）

0 引言

随着飞机多电和全电供电技术的迅猛发展，导致电缆和导线的使用量增多，由于长年累月的使用，深埋在飞机结构之中的总长可达几十万米的线缆难免会产生裂纹和磨损现象[1-2]，加上周围环境中各种物质对线路的侵蚀和飞行过程中振动等恶劣条件的影响，极易诱发电弧故障。飞机上原有的热保护断路器（Thermal Circuit Breaker ,TCB）和固态功率控制器（Solid State Power Controller, SSPC）用来在过电流或者短路的情况下对电线进行过热保护，然而串联型电弧故障电流信号往往比正常电流信号的幅值要小，达不到过电流保护器的额定值。因此，研制有效的电弧故障断路器（Arc Fault Circuit Breaker,AFCB）具有十分重要的意义。

串联电弧故障的检测方法主要分为两类：一类是分析电弧故障产生时的物理现象进行识别[3-4]；另一类是通过分析电弧故障发生时线路中电压和电流信号的时域、频域和时频域特征的变化情况进行诊断[5-8]。在文献[9]中设计了一种用于测量电弧电磁辐射的Hibert的分形天线，研究了电弧故障的电磁辐射信号特征及其测量方法。文献[10]中计算了电流信号的平肩时间、脉冲数量和随机性参数并对其进行组合，通过电流与电压的相位关系对故障负载进行分类并确定阈值来诊断电弧故障的发生。文献[11-12]在提取特征量的过程中都用到了小波变换，小波变换能够清楚地描述信号频率分布随时间变化的关系，是分析非平稳信号的有力工具。文献[13]中采用希尔伯特黄变换提取了电弧电流交流分量的时域和频域特征量区分电弧故障，虽然在经验模态分解过程中能够保留非线性非平稳信号的故障特征，但是在分解时会出现模态混叠现象并且不能预先确定分解的级数。

由于时域特征的统计学分析方法简单、便于工程实现，近些年来受到了广泛的研究。这类方法主要是对电弧故障发生前后电流信号的变化情况进行检测，一方面是基于电流信号的局部特征的变化情况，特征量主要有均值、标准差、方均根值和峭度等，这些特征量能够在一定程度上反映电弧故障信号中“毛刺”和“零休”的特征，但是当故障局部特征变化不明显时会导致检测效果不理想；另一方面是基于电流信号的整体变化情况提取时域特征量，如变异系数[14]、相关系数和偏态指标等，这些特征量对于线性负载识别效果较好，但是当负载为非线性负载时，正常与故障情况下都会产生高次谐波，导致区分故障情况时容易发生误判。针对以上情况，本文提出一种基于Levene检验的时域分析方法，Levene检验既可以用于正态分布的数据，也可以用于非正态或分布不明的数据，因此在进行故障分析时有较好的适用性，并且在检验时具有较好的稳定性和把握度，该方法目前多用于卫生统计方面，还未见在电弧故障诊断领域的文献论述。

目前，电子技术的应用越来越广泛，从日常生活中的电气设备到飞机上的设备，其中非线性或含有非线性成分的设备使用急剧增加。由于非线性负载的电流成分更加复杂并且谐波含量较高，加上航空电源（115V/400Hz）频率相比民用电源高导致电流周期短，因此对于航空串联电弧故障检测方法的适用性和实时性提出了更高的要求。本文首先以点接触实验数据为例，采用Levene检验对数据进行分析并提取P值（显著性水平）作为时域特征量，通过与统计学时域方法峭度、偏态指标和相关系数的分析结果进行对比，表明该特征量在串联电弧故障发生前后变化明显，利用该方法进行航空串联电弧故障识别准确率更高。最后选用碳化路径实验负载数据和本文分析所用之外的点接触实验负载数据对该方法的有效性进行测试。

1 航空串联电弧故障实验

1.1 电弧模拟实验方案

依据标准 UL 1699[15]和 GB/T 31143—2014[16]搭建点接触和碳化路径电弧故障实验电路如图1和图2所示。图中，点接触实验通过调节步进电机使两触头之间产生模拟电弧故障，选用多种负载进行多次实验数据采集，其中，线性负载包括57Ω、7Ω+7mH和 57Ω+47μF，非线性负载是自耦变压整流器（Auto Transformer Rectifier Units, ATRU）。碳化路径实验首先烧制导线，导线依据标准GB/T 31143−2014进行制备，如图3所示，选取两根长度至少200mm的按照GB/T 5023中IEC 02分类的聚氯乙烯导线，将两根导线从中间切开 50mm，使得绝缘皮中的导体裸露但不对其造成损害，再用聚氯乙烯电气绝缘带把导线切口包裹两层，在导线的两端将绝缘层剥开 12mm用以连接实验电路。实验时接通 220V/50Hz电源直到导线停止冒烟时断开；然后接通115V/400Hz电源，若指示灯为断断续续的闪亮情况，则说明碳化路径烧制成功有电弧产生，实验负载选择为 7Ω+7mH 和 30Ω+47μF。

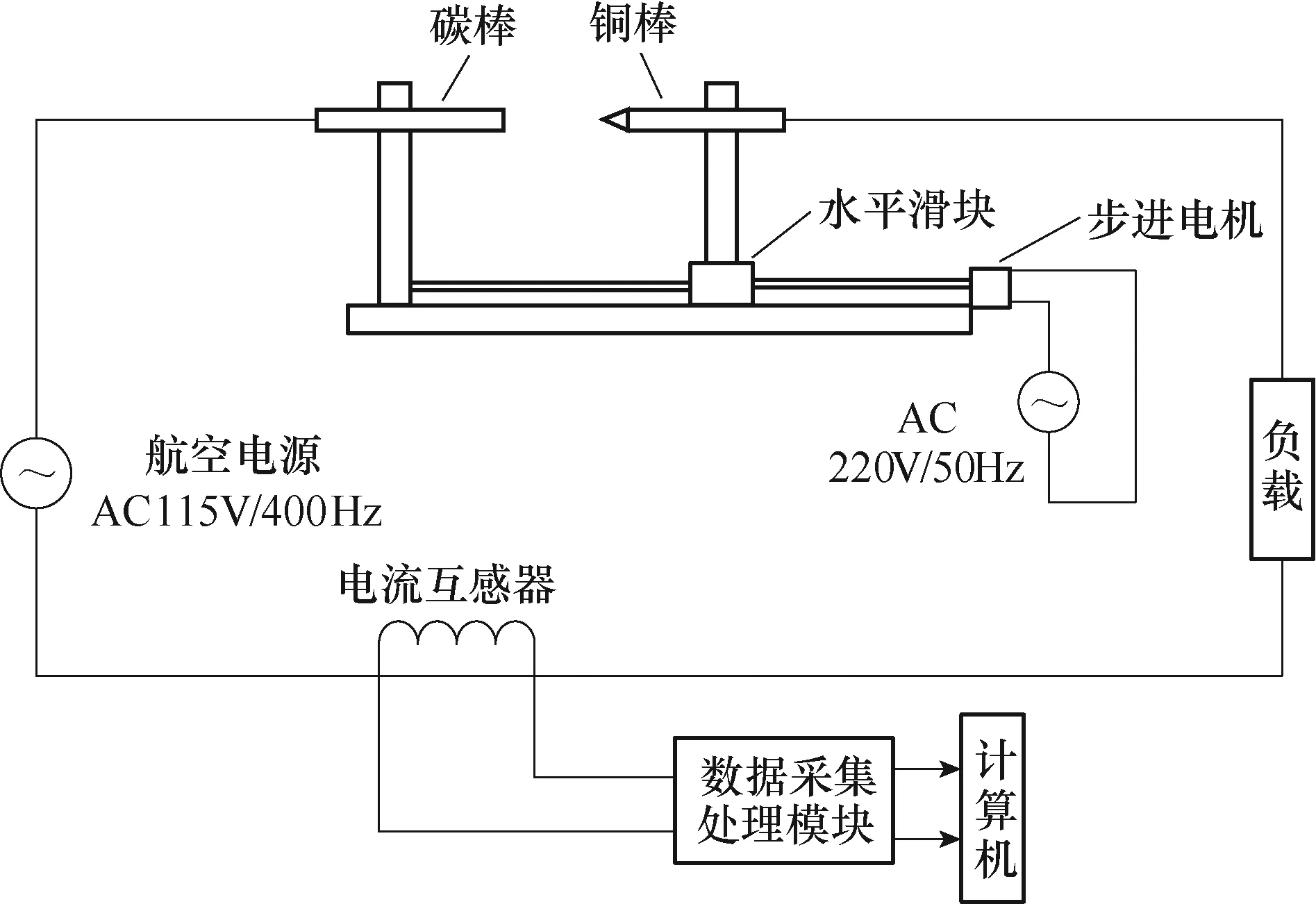
图1 点接触实验电路Fig.1 Circuit diagram of point contact experiment

图2 碳化路径实验电路Fig.2 Circuit diagram of carbonization path experiment

图3 碳化路径导线示意图Fig.3 Diagram of carbonization path conductor

1.2 实验结果

在实验中每个电流信号周期采集 1 024个点，其中采集的点接触实验电流信号波形如图4所示（从正常信号到故障信号20个电流周期信号），碳化路径实验电流信号波形如图5所示。

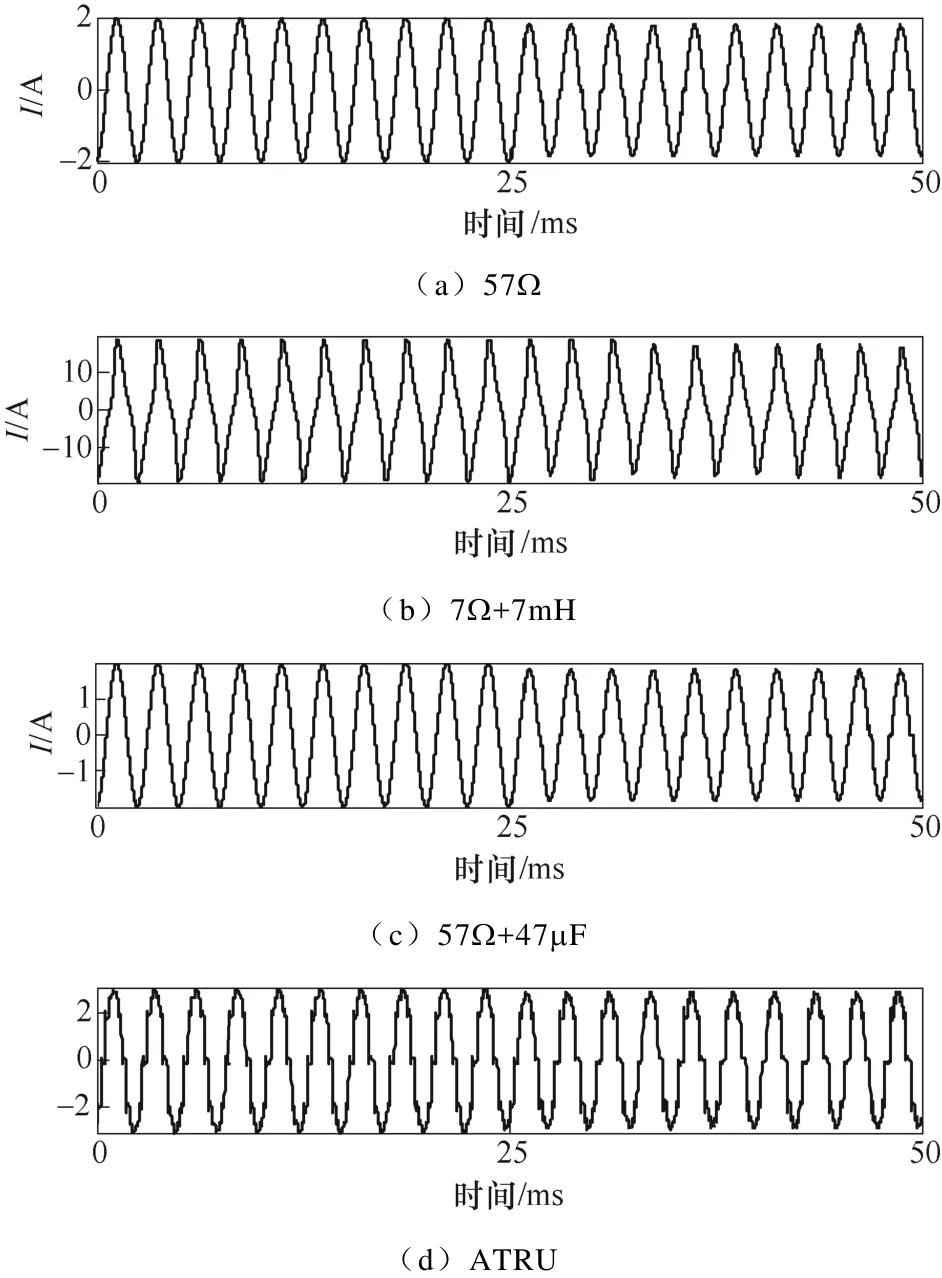
图4 点接触实验电流信号波形Fig.4 Waveforms of point contact experiment current signal

图5 碳化路径实验电流信号波形Fig.5 Waveforms of carbonation path experimental current signal

通过图4可知，对于负载 57Ω和 57Ω+47μF，正常工作时，电流波形为正弦波，发生电弧故障后，在电流过零点附近出现“零休”现象，高次谐波含量明显增多并且电流幅值降低；负载7Ω+7mH在发生故障后电流幅值降低，但是基本无“零休”和“毛刺”现象，并且正常波形形似正弦波。产生这种现象是由于电阻值较小，电路负载接近于纯电感型，而电感具有“通直流、阻交流”的作用。对于非线性负载，无论正常还是故障情况，其电流信号中都含有高次谐波，但在发生故障后谐波含量更高，波形幅值降低。观察图5可以看出，碳化路径实验相比于点接触实验电弧故障信号的“零休”时间更长，故障特征更加明显，这是由于在点接触实验中通过控制电机的移动可以产生稳定的电弧，而碳化路径实验中产生的电弧不稳定，燃烧现象断断续续，因此波形变化特征比较显著，出现了非常明显的“零休”现象。综上可知，在发生串联电弧故障后电流波形均出现不同程度的变化。

2 串联电弧故障特征量的提取

2.1 方差齐性检验方法分析

方差齐性检验是数理统计学中检查不同样本的总体方差是否相同的一种方法。其基本原理是，先对总体的特征作出假设，然后通过抽样研究的统计推理，对此假设应该被拒绝还是接受作出推断。目前，统计学中方差齐性检验方法主要有 Levene检验、Hartley 检验、Bartlett检验和 Cochran 检验[17-18]。其中，Levene检验既可以用于正态分布的总体，也可以用于非正态分布的总体或分布不明的总体，具有较好的稳健性[16]，是最标准的方差齐性检验方法。

2.2 Levene检验

Levene检验也称为 Levene方差齐性检验，是对方差模型的残差进行组间齐性检验，最早由H.R.Levene在 1960年提出[19]，在 1974年经过 M.B.Brown和A.B.Forsythe对其进行扩展之后[20]，应用范围变得更加广泛并且检验效果较理想，主要用于检验两个或两个以上样本间的方差是否齐性。

由于常规的检验过程比较繁琐，为了节约时间成本，在电弧故障检测过程中只提取显著性水平P值。将实验中采集的每个电流信号周期的数据分别看成一组抽样样本，通过Levene检验计算两个不同样本的P值。首先选取两组采集的实验电流信号数据Yi，i=1、2，Yij为第i组样本中的第j个样本，计算过程如下：

（1）将原始数据转换为新的变量值。

式中，Zij为转换之后的新变量值；为第组原始数据的算数平均值。

（2）计算Levene检验的统计量W。

式中，k为样本组数；Ni为第i组样本含量；N为全部样本之和；为第i组样本组内均值；为各组全部数据总的均值。

（3）计算P值。

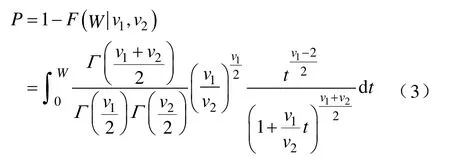
式中，自由度v1和v2分别为k−1、N−k。

2.3 时域特征量的提取

检测结果P值为可信水平的一个递增指标，P值越小，越不能认为样本中变量的关联是总体中各变量关联的可靠指标，也就是说，P值越小，两个样本之间的差异越大。对于检测的两组电流信号样本而言，P值越大，说明两组样本相似度越高；反之，则说明其中一组电流信号样本畸变越严重。

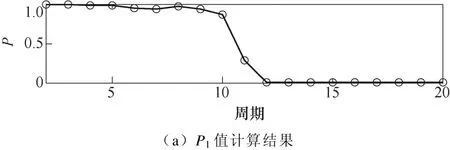
对于检验中样本的选择提出了两种不同的方法：首先选取一个正常电流信号周期的数据作为正常样本，然后对之后的每一个电流信号样本和正常样本进行 Levene检验，检测结果记为P1；不选取正常样本，对每一个电流信号样本与前一个电流信号样本进行 Levene检验，检测结果记为P2。以纯阻57Ω 为例（电流信号波形见图4a），两种检测方法的结果如图6所示。

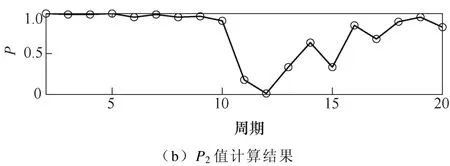
图6 不同检测方法结果Fig.6 Results of different detection methods

观察对比两种检测方法的结果，发现在发生电弧故障后P1值出现了明显的下降；P2值也出现了下降，但是没有P1值稳定，这是因为相邻故障电流信号周期之间虽然存在差异，但是在电弧稳定燃烧时故障电流信号周期之间的相对差异比较小，导致在区分故障情况时效果不理想。因此，方法1相比于方法2区分正常与故障情况的效果更好。采用方法1计算各负载发生电弧故障前后的P值，计算结果统计见表1（保留到小数点后四位）。

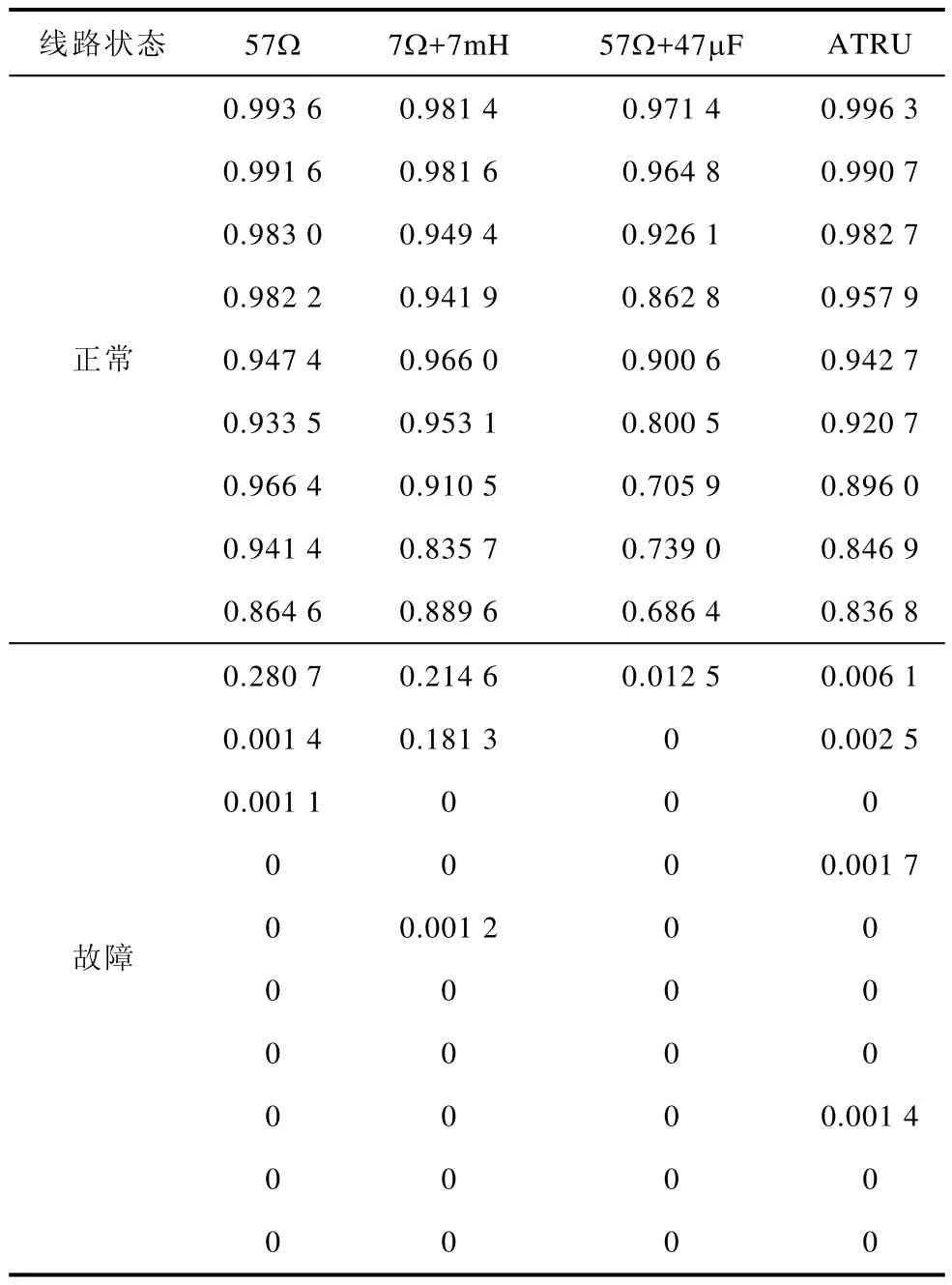
表1 各负载P值的计算结果Tab.1 Calculation results of P value of each load

观察表1，通过对比各个负载在电弧故障发生前后的P值发现，在故障发生前基本都稳定在0.6～1.0之间，而发生电弧故障后P值下降到了0.3以下，能明显地区分开正常与电弧故障情况。选取具有代表性的统计学时域方法峭度、偏态指标和相关系数与 Levene检验进行对比。其中，峭度是归一化 4阶中心矩，该参数可以检测电流信号的高频尖刺部分；偏态指标又称为三阶累积量，反映信号概率密度分布，主要用来量度统计数据分布的不对称程度或偏斜程度；相关系数反映两个变量间的线性关系，可以用来量化两个波形之间的相似程度，在计算时选定一个正常周期为样本，再计算其余信号周期与正常样本的相关系数值。以图4中的实验数据为例，峭度值、偏态指标和相关系数值计算结果分别如图7～图9所示。

图7 峭度值计算结果Fig.7 Calculation results of Kurtosis

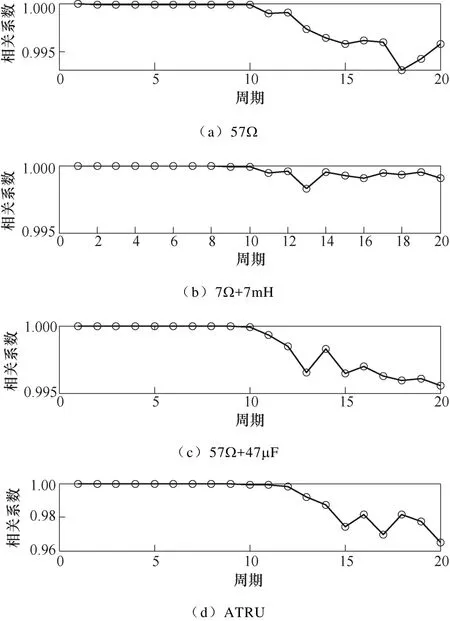
图9 相关系数值计算结果Fig.9 Calculation results of correlation coefficient value

通过观察图7～图9发现，图7d由于非线性负载ATRU正常与电弧故障情况下电流信号成分都比较复杂并且含有“毛刺”，致使发生故障后畸变不严重的电流信号周期的峭度值基本无变化；在发生故障后有些故障电流信号周期也呈对称变化，导致图8中有些故障周期的偏态指标与正常情况区分不开；相关系数值与P值在这里本质上都用来反映两个电流信号周期波形的相似程度，但是由图9b可知，负载7Ω+7mH由于发生故障后无明显“零休”和“毛刺”现象，使得正常与故障信号的相关系数值变化不明显，整体情况相比之下P值（计算结果见表1）区分效果和稳定性更好，在区分电弧故障情况时避免了以上问题。

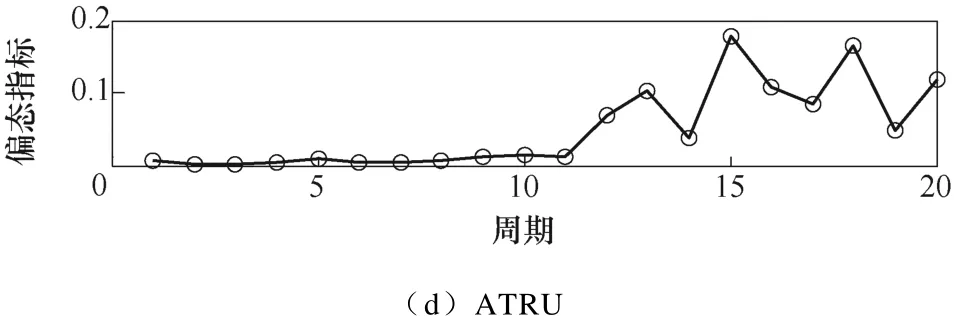
图8 偏态指标计算结果Fig.8 Calculation results of Skewness index

3 基于PSO_SVM的特征量识别准确率对比

3.1 识别算法

为了进一步量化比对这四种统计学时域方法，通过支持向量机（Support Vector Machine, SVM）[21]来测试各种特征量的识别准确率。在用 SVM 做分类预测时需要调节惩罚参数c和核函数参数g才能得到比较理想的预测分类准确率，为得到最优参数，选用粒子群优化（Particle Swarm Optimization, PSO）算法[22-23]来寻找c和g。PSO_SVM计算步骤如下：

（1）导入训练集和测试集数据。

（2）初始化粒子群，设定各类参数。设目前位置是每个粒子的初始位置，从中选取出全局最优极值，并标记其最优值序号及位置。

（3）对粒子的速度和位置进行更新，评价每个粒子，并根据定义的适应度函数，计算每个粒子的适应值，进行个体极值更新。如果每个粒子个体最优值中最佳位置是目前全局的极值，那么把个体极值规定成最优位置，完成群体最优更新。

（4）检验是否可以终止。若达到最大迭代次数，则输出最优参数c和g；反之，返回步骤（3）继续进行寻优。

（5）选取好最优的参数c和g之后，进行SVM识别，得到在最优参数下的识别准确率。

3.2 识别结果

每种特征量选取各种负载在正常运行和电弧故障时的各20组数据（共160组数据）作为训练集，将数据代入通过PSO优化的SVM中进行训练后，用同样的方式再选取160组数据作为测试集。其测试情况见表2（由于不同负载的峭度值存在混叠，所以首先对提取的特征量进行归一化再识别）。

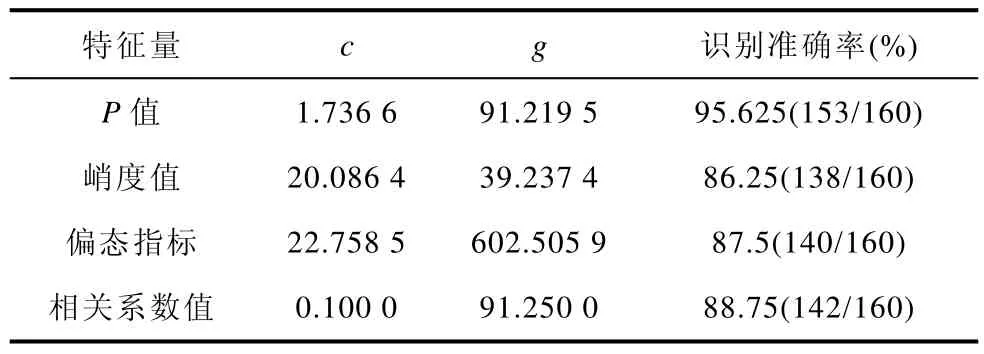
表2 各特征量识别结果Tab.2 Recognition result of each feature

由表2可知，特征量P值的识别准确率高于峭度值、偏态指标和相关系数值，达到了 95.625%，相比于目前统计学时域方法，该方法有着突出的优势，更适合应用于航空串联电弧故障检测。

3.3 测试结果及阈值选取

为了检测该方法的可靠性，选择点接触实验负载 7Ω、57Ω+5mH、57Ω+25μF、ATRU+115Ω 和碳化路径实验负载 7Ω+7mH、30Ω+47μF作为测试负载，对各种负载分别提取40组正常与40组电弧故障情况下的特征量作为测试集，并代入已经训练好的PSO_ SVM中进行识别，其结果见表3。

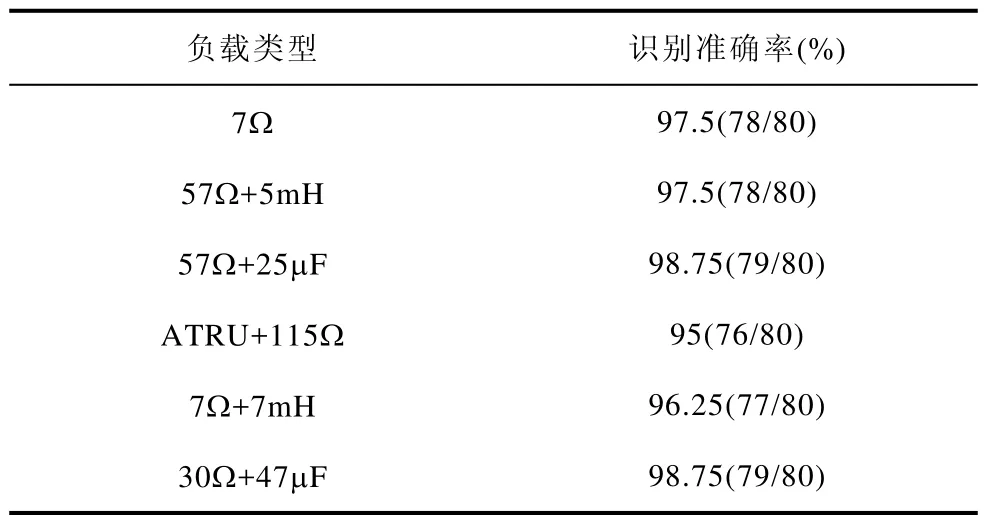
表3 各测试负载识别结果Tab.3 Identification results for each test load

由表3统计结果可知，在测试中负载57Ω+25μF和30Ω+47μF的故障识别准确率最高达到了98.75%，而负载 ATRU+115Ω 的准确率最低为95%。综合整体情况来看，对于各种测试负载的识别准确率均在95%以上，表明该种方法在判别是否有电弧故障发生时具有较高的可靠性和实用性。

考虑到正常与电弧故障电流信号的P值计算结果有着显著差异，为了使诊断方法具有更好的实时性，可通过设定阈值进行电弧故障识别。由表1可知，正常与故障电流信号的P值分别集中在 0.6～1.0和0.3以下，所以需在0.3～0.6之间设定阈值，为合理设置阈值，以0.1为间隔选取了4个不同的阈值，并随机选取正常与故障各80组数据进行识别准确率测试，结果见表4，可以看出，阈值设为0.5时识别准确最高为96.875%。

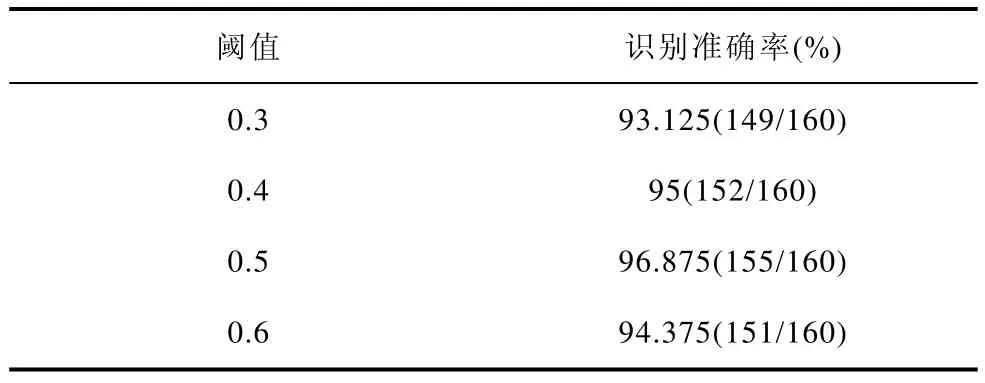
表4 不同阈值下的识别结果Tab.4 Recognition results under different thresholds

4 结论

本文针对目前串联电弧故障识别中统计学方法的局限性，提出利用Levene检验对电弧故障发生前后的电流信号进行分析并提取特征量。在点接触实验中发现，当负载为7Ω+7mH时，由于负载类型接近于纯电感性，导致在发生故障后电流信号的局部变化不明显，对诊断方法提出了更高要求。将常用统计学方法峭度、偏态指标和相关系数的 PSO_SVM识别准确率与Levene检验进行对比，结果表明，Levene检验的识别准确率均高于其他三种方法，能够有效地区分电弧故障情况，为研制航空电弧故障断路器提供了可靠的参考依据。由于电弧故障发生前后的P值出现了显著差异，根据特征量的变化情况可以将阈值设为0.5衡量故障是否发生。