基于多分支BP神经网络的气动肌肉迟滞建模方法
谢胜龙,张文欣,张为民,任国营,鲁玉军,鲁 庆
(1. 中国计量大学 机电工程学院,浙江 杭州 310018;2. 浙江西子重工机械有限公司,浙江 嘉兴 314423;3. 中国计量科学研究院,北京 100029;4. 浙江理工大学 机械与自动控制学院,浙江 杭州 310018;5. 宝武装备智能科技有限公司,安徽 马鞍山 243000)
1 引 言
气动肌肉(pneumatic muscle,PM)由于具有成本低、安装方便、结构简单、重量轻、输出力/自重比大以及突出的柔顺性等优点[1],因而被广泛应用于手术、康复、仿生和救援机器人等领域[2]。然而,由于组成气动肌肉的橡胶管的高弹性和气体的可压缩性,其在应用过程中会有明显的迟滞现象,从而给气动肌肉的控制系统带来强非线性,进而给其精确的控制带来巨大的挑战[3]。目前,构建气动肌肉迟滞非线性现象的数学模型主要有微分型迟滞模型和积分型数学模型[4]。微分型迟滞模型采用非线性微分方程描述气动肌肉的迟滞特性[5],主要有Duhem模型和Bouc-Wen模型等。文献[6]采用Bouc-Wen模型来捕捉气动肌肉中的迟滞现象,并采用单神经元自适应PID算法研究了一种气动肌肉驱动的机械手的控制性能。在此基础上,文献[7]采用Duhem模型描述气动人工肌肉的迟滞现象,并借助于神经网络方法对模型中的参数进行了辨识;Aschem-ann[8]采用广义Bouc-Wen模型建立了气动肌肉的力/长度迟滞模型,结果发现该模型的建模效果比Maxwell模型和Prandtl-Ishlinskii (PI)模型的效果更好。积分型迟滞模型又称为算子型迟滞模型,它借助一定数量算子的加权叠加来拟合迟滞曲线[9]。根据所采用迟滞算子的不同,常见的积分型迟滞模型主要有Preisach模型和PI模型等。Kosaki[10]采用学习矢量化方法,并基于Preisach模型来描述随负载变化的气动肌肉气压/位移迟滞特性,实验结果证实学习矢量化网络方法和迟滞补偿的引入显著提高了气动人工肌肉的控制精度。由于运动速度的变化也会使得气动人工肌肉的迟滞特性发生改变,因此Kosaki[11]在气动人工肌肉的轨迹跟踪控制中借助于自适应参数辨识方法对Preisach模型中的参数进行在线辨识,取得了良好的控制效果。针对现有文献中对气动肌肉长度/气压迟滞建模研究较少的现状,谢胜龙分别采用广义PI (GPI)模型[12]和修正广义PI (MGPI)模型[13]刻画气动肌肉的位移/气压迟滞现象,取得了良好的效果。臧希喆[14]采用修正PI模型研究了气动肌肉的长度/气压迟滞现象,文献[15]采用克里格空间插值法对气动肌肉的迟滞进行了建模研究,均取得了较好的效果。文献[16]基于Gaussian混合模型对气动肌肉的收缩段和伸长段分别进行建模,并与GPI和MGPI模型的建模精度进行了对比研究,发现该模型的建模精度更高。上述两类模型中,微分型模型在参数辨识过程需要求解微分方程,因此存在参数辨识计算复杂的问题。而积分型迟滞模型由于采用算子拟合思想,因此模型复杂度较高,参数辨识计算量大。近年来,由于神经网络能够很好地逼近任意连续曲线,而且在运行速度上也比常规的非线性迭代算法更有优势,因此开始逐渐被应用于气动肌肉的迟滞建模中,并取得了一定的成果[17,18]。然而,神经网络在预测问题中普遍存在过拟合问题,即网络拟合精度越高,泛化能力越差[19]。为解决上述问题,有学者从网络结构、样本质量和训练参数设置等方面对其开展了研究,但这些方法普遍存在容易陷入局部极小点、精度降低和效率降低等问题[20],且未应用于气动肌肉的迟滞建模中。
本文提出一种多分支BP神经网络模型,对气动肌肉迟滞曲线的充气收缩和放气伸长两阶段的曲线分别进行训练建模,避免传统BP神经网络的过拟合现象以提高模型的预测精度。同时与传统BP神经网络和PI模型的辨识结果对比,以说明其在建模精度上的优越性。最后利用训练好的BP神经网络模型预测气动肌肉在另一组气压输入下的迟滞曲线,验证该模型的泛化能力。
2 基础理论
2.1 PI模型
作为Preisach模型的一种改进模型,PI模型由有限个线性play算子加权叠加构成(如图1所示),每一个线性play算子由一个阈值r确定,其中的任意一个线性play算子均可用于描述简单的迟滞现象。由于PI模型的逆模型是解析的,因此得到了广泛的应用。

图1 PI模型Fig.1 PI model
通过对不同阈值的线性play算子线性加权叠加即可得到PI模型,第i个算子表达式和初始条件如式(1)和式(2)所示。
yi(k)=max{x(k)-ri,min[x(k)+ri,yi(k-1)]}
(1)
yi(0)=max{x(0)-ri,min[x(0)+ri,yi0]}
(2)
式中:n为线性play算子的个数;x(k)为实验中k时刻的输入;yi(k)为第i个算子在k时刻的输出;yi(0)为各个算子初始输出;线性play算子初始状态向量为y0=[y10,…,yn0],且yi0=0,i=1,…,n;ri为阈值,阈值向量r=[r1,…,rn]。将各线性play算子分别乘以各自的权重后再相加,即可得到PI模型。其输出公式为:

(3)

2.2 BP神经网络
BP神经网络是一种多层前馈神经网络,它由输入层﹑隐含层和输出层组成,典型的3层BP神经网络拓扑结构如图2所示。

图2 BP神经网络Fig.2 BP neural network
BP神经网络的训练过程如下:
2) 正向输出计算:输入实验样本数据,采用第(1)步中初始化的权重系数分别计算神经网络中所有神经元的输出;
3) 反向误差计算:根据步骤2)中实验样本数据中的期望输出和所有神经元的输出,反向计算所有神经元的输出误差;

5) 循环判断与终止:如果3)中的误差没有达到期望值,或者没有达到事先规定的迭代次数,跳转至步骤2)继续循环计算;如果满足要求,则终止迭代计算,记录网络最终的权重系数与训练误差。
训练过程通过预测误差来不断地调整整个网络模型中的权重系数和阈值,使得网络的输出不断地逼近期望的输出,从而完成模型的训练。
3 实验研究
3.1 实验平台
气动肌肉的位移/气压迟滞实验装置如图3所示。

图3 气动肌肉迟滞特性实验平台Fig.3 Experimental apparatus for hysteresis characteristics of PM
该实验平台由气动肌肉、比例调压阀、空气压缩机、位移传感器、气压传感器和计算机组成。气动肌肉(型号DMSP-20-500 N,直径20 mm,长500 mm)为德国费斯托公司所生产,其一端固定于机架上,另一端可自由移动。位移传感器(型号TEX-0150-415-002-205,量程150 mm)一端固定于机架上,另一端则与气动肌肉的自由端通过连接件相连,用于实时测量气动肌肉运动过程中的位移值。气压传感器(型号SDE1-D10-M8-G5,最大测量气压1 MPa)与气动肌肉内腔相连,用于实时测量气动肌肉内腔的气压值。本文借助LabView编写气动肌肉的控制和数据采集程序,控制程序生成的控制信号通过数据采集卡(型号PCI-6230,8路模拟量输入,4路模拟量输出)的模拟量输出接口(AO)控制比例调压阀(型号VPPM-6L-L-1-G18-0L10H,气压调节范围0~1 MPa)的电压变化,进而控制气动肌肉内腔的气压变化,从而驱动气动肌肉的伸缩运动;数据采集程序用于采集气动肌肉运动过程中的位移和气压信号,实验中的气压和位移信号通过数据采集卡的模拟量输入接口(AI)传输入数据采集卡中,数据采集卡再通过PCI总线与计算机通信,传输入计算机中进行数据的存储、数据处理和分析。
3.2 实验过程
实验过程如下:调节气动肌肉,使其初始状态下时内部气压等于大气压。启动LabView编写的控制程序,调节比例调压阀,控制气动肌肉内部绝对气压缓慢地从0 MPa增加到0.6 MPa,当其内部气压到达0.6 MPa后,再调节比例调压阀,控制其内部绝对气压缓慢降到0 MPa。通过LabView编写的数据采集程序可得到气动肌肉充放气过程中的气压和长度数据。实验得到的气动肌肉位移/气压迟滞模型如图4所示。

图4 气动肌肉位移/气压迟滞Fig.4 Displacement/pressure hysteresis of PM
从图4中可以看出,气动肌肉充气时收缩,气动肌肉从点A运动到点B;放气时伸长,从点B运动到点A。在充气过程中,当气压增加到P时,对应的气动肌肉的长度为A1P1,对应图中的Pc点;在放气过程中,当气压减小到P时,对应的气动肌肉的长度为A1P2,对应图中的Ps点。显然,Pc点与Ps点并不重合,两者之间不重合的现象即为迟滞现象。在采用BP神经网络建模时,传统的方法是使用BP神经网络对整个迟滞环建模,本文提出的方法则采用2个BP神经网络分别对迟滞环的充气收缩段和放气伸长段建模,又称为多分支BP神经网络。
3.3 BP神经网络训练与预测
基于BP神经网络的气动肌肉迟滞建模可以分为网络模型的构建和模型权值的训练两步,在模型确定后可以进行模型的输出预测,具体的流程如图5所示。

图5 BP神经网络建模与预测流程Fig.5 Training and forecast process of BP neural network
根据文献[21]的研究,仅一个隐含层的BP神经网络便有足够的精度逼近任意的连续函数,因此本文所用的神经网络采用一层隐含层结构。神经网络的构建通常需要根据所拟合非线性函数的特点来确定其网络结构参数。根据图4中气动肌肉的位移/气压迟滞曲线可知,系统的输入为气压,输出为气动肌肉的收缩率,因此本文的神经网络模型采用1-n-1型结构:其输入层与输出层均只有1个节点,中间的隐含层包含n个节点。鉴于隐含层的节点数对模型的精度有很大的影响,本文将采用试凑法研究节点数对BP神经网络建模精度与预测精度的影响。
本实验所用测试数据和训练数据如图6所示,两者是随机抽取气动肌肉位移/气压迟滞曲线中的两条分别作为训练数据和测试数据。从图中可见两者并不完全重合,训练数据的范围比测试数据的稍大,产生该误差的原因主要有比例阀的控制电压的误差和在气动肌肉往复运动过程中因橡胶管的柔性产生的蠕变[22]。

图6 训练数据与测试数据Fig.6 Training data and testing data
4 结果分析
图7~图9为3种模型的建模结果与建模误差。对比3图可以发现,BP神经网络的拟合精度明显高于多分支BP神经网络和PI模型,三者的建模精度从高到低依次为:BP神经网络,多分支BP神经网络和PI模型。

图7 BP神经网络辨识结果Fig.7 Identification results of BP network

图8 多分支BP神经网络辨识结果Fig.8 Identification results of multi-branch BP network

图9 PI神经网络辨识结果Fig.9 Identification results of PI model
为了量化分析各模型的参数辨识与模型预测效果,本文根据文献[13]所述公式计算理论模型与实际实验数据之间的均方差和平均误差:
emax=|max(y)-min(yM)|
(4)
(5)
(6)
所得的最大误差emax、平均误差erms和均方差emae以及2种模型在不同算子和次数下的计算时间如表1和表2所示。
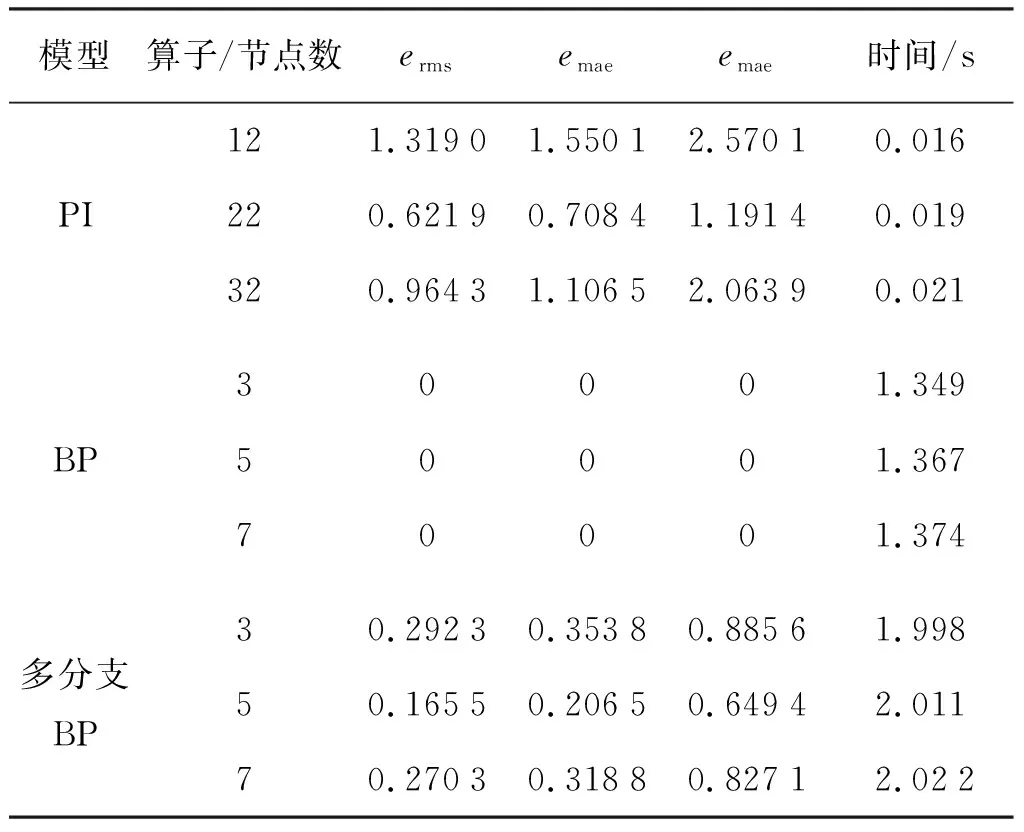
表1 模型建模误差比较Tab.1 Modeling errors comparison of two modelsmm

表2 模型预测误差比较Tab.2 Forecast errors comparison of two modelsmm
图10和图11为BP神经网络模型与多分支BP神经网络模型的预测结果与预测误差。可见在预测模型方面,多分支BP神经网络模型的效果明显优于BP神经网络。结合表1和表2可见,在用BP神经网络拟合整个迟滞环的的时候误差基本为零,精度远高于多分支BP神经网络,但是在预测模型模型误差时,建模精度明显低于多分支BP神经网络。这种在训练数据上能够获得比其他假设更好的拟合,但是在训练数据外的数据集上却不能很好地拟合数据的现象称为过拟合现象。产生该现象的可能原因主要有:1) 实验数据样本数量较少,不够全面;2) 实验数据样本噪音数据干扰较大;3) 因迭代次数过多,神经网络的权值分布向样本数据中的无关特征和噪声数据倾斜。因此在实验过程中需要采用有效的数据滤波手段以降低噪音对建模的影响,同时要选用合理的训练数据,避免因数据量过少产生的误差。但是数据量过大也会导致训练时间增加,因此要合理选用训练数据。

图10 BP神经网络预测结果Fig.10 Forecast results of BP network

图11 多分支BP神经网络预测结果Fig.11 Forecast results of multi-branch BP network
表1表明,PI模型的建模精度并不是随着算子个数的增加而单调递增,超过一定的算子个数时,PI模型的建模精度反而随着算子个数的增加而减小,而其计算时间则与算子个数呈正相关关系。因此在采用PI模型建模时需要控制算子个数,实现建模精度与计算时间的折中。
由计算时间,可以看出PI模型计算所需时间最短,BP神经网络和多分支BP神经网络计算时间明显多于PI模型,这是由于BP模型的缺点是学习过程很长,学习收敛性较差,随着样本数据的增加,训练所需时间也会增加,因此需要控制训练样本数据量。同时,多分支BP神经网络计算时间较BP神经网络有明显增加,这是由于模型中有2个BP神经网络,因此计算时间会有一定程度的提高,可见多分支BP神经网络虽然避免了BP神经网络的“过拟合”现象,却是以牺牲计算时间为代价的,后面将在此基础上寻求新的改进方法。需要指出的是,对于PI模型,随着算子个数的增加,计算时间呈现稳定的增加,但是对于BP神经网络和多分支BP神经网络而言,随着节点数的增加,计算时间并非严格增加,甚至可能出现变小的现象。主要原因一方面是隐含层节点数差别不明显,而且数据量不大,因此导致计算时间区分不明显;另一个原因是因为BP神经网络容易陷入局部最优值,从而导致计算时间缩短。这里给出的是多次计算后的平均值,用于直观上比较模型在不同隐含层节点个数时训练所需的计算时间。
表1表明,当节点数为5时,多分支BP神经网络建模时的平均误差、均方差与最大误差相较于PI模型减小了87.45%,86.68%与74.73%。表2表明,相较于容易产生“过拟合”现象的传统BP神经网络,多分支BP神经网络预测时的平均误差、均方差与最大误差分别减小了16.46%,22.92%与36.91%。需要指出的是,无论是对于BP神经网络还是对于多分支BP神经网络而言,其建模精度与模型预测精度并不是节点数越多越好,网络模型中的隐含层节点数目对模型的精度有着至关重要的影响:节点数较少时,网络的学习与泛化能力较差,模型精度也随之降低;节点数增加时,网络的过拟合风险也随之增加,导致模型的建模精度和预测精度均明显降低。实际应用时,需要合理选用神经网络隐含层的节点数。
5 结 论
针对气动肌肉运动过程中的位移/气压迟滞非线性现象,本文提出多分支BP神经网络对其位移/气压迟滞开展了建模研究,通过采用多分支BP神经网络分别拟合气动肌肉迟滞曲线的充气收缩段和放气伸长段,能很好地避免传统BP神经网络的过拟合现象,且其建模精度明显优于PI模型,各项误差指标均明显低于PI模型。后续工作中将基于该方法研究气动肌肉的控制。

