供水管网防护设施数值模拟研究
付海林,刁新伊,张小莹
(1. 新疆农业大学水利与土木工程学院,新疆 乌鲁木齐 830052;2. 察布查尔锡伯自治县农业农村局,新疆 伊犁 835300)
1 概述
供水管网被誉为城市的“生命线”,它的主要功能是将来自于较集中点(如输水管渠的末端或贮水设施等)的水量分配输送到整个供水区域,使用户能从近处接管用水,是社会生产和居民生活的重要基础设施[1- 2]。近年来,随着我国经济迅速发展,城市规模逐渐扩大,人口的增长和人民生活水平的提高,水资源的利用不断加剧[3- 4],配水管网的安全建设占据了越来越重要的地位。由于先前管网规划具有盲目性,管线连接的随意性较大,且管理手段较为落后,导致管网布置存在各类问题。目前,水力与水质模拟软件的应用已成为大型给水管网分析的主要手段,通过建立给水管网模型系统实现管网运行状态的实时分析,通过改变边界条件从而降低供水管网的水量消耗,以实现管网管理的科学调度。在给水管网水力模拟计算中,EPANET软件是最为常用且计算精度较高的软件,该软件主要用于有压管网系统水力计算和水质分析[5]。EPANET管网模型提供了包括管道、节点、水泵、阀门和蓄水池等组件,并且实时读取管道流量、节点压力、水池水位高度等参数,可实现不同类型的配水系统分析。
因为EPANET软件自身存在方便性及直观性等优点,已被国内外学者广泛应用于有压管网的平差计算[6- 8]。张凤娥[9]应用EPANET水力计算软件建立管网水力计算模型,缩短了管网平差的计算时间,大大提高了计算效率和精确度;张凤娥等人[10]对位于常州市新北区的罗溪镇供水管网进行EPANET平差计算,将平差压力和实测压力进行比较,判断管网出现问题的原因;杨根全[11]在安哥拉供水项目中采用EPANET软件,在管网中加入水塔,进行管网平差计算,对水塔不同水位进行模拟,最终确定水塔高度;陶涛、张俊[12]等人将布谷鸟算法与EPANET软件结合,利用布谷鸟算法对真实管网中阀门控制策略确定最佳方案,大大缩小了计算量。以上关于管网模型的研究或对管网界面、模块、操作流程进行介绍,或对实际工程中无法保证管网中各节点压力最低要求情况提出增大管径或提高扬程的解决方案,或在考虑安全经济前提下对管网布置方式进行优化设计,但均未对输水管网中产生负压或正压过大等情况进行布设防护设施以降低管道压力的研究。本文基于前人的研究成果,以某实际工程供水管网为研究对象,根据实际地形及供水量等水力条件通过EPANET软件建立数学模型,结合穷举法优化算法[13],通过软件自身运行得到的数据反馈,不断改进模型,确定较优的供水管网结构配置,计算结果可为此类工程提供布置参考。
2 数学模型及计算方法
2.1 管网模型
管网水力模型的建立主要根据节点流量平衡方程、能量平衡方程、管道压降方程及Hazen Williams水头损失公式。节点流量平衡方程为:
∑Qi+∑Qij=0
(1)
式中,Qi—流入或流出节点i的集中流量,m3/s;Qij—节点i流向节点j的管道流量,m3/s。
节点能量平衡方程为:
∑hij=0
(2)
式中,hij—管段(i→j)的水头损失。
管道压降方程,表示管道的水头损失与管道两端节点压力水头的关系:
(3)
式中,hij—管道水头损失,m;Hi、Hj—节点i、j的总压力水头,m;Sij—管道摩阻。
由于管道较光滑,本文水头损失采用Hazen Williams公式计算,公式如下:
(4)
式中,h—水头损失,m;l—管段长度,m;D—管段管径,m;q—管段流量,m3/s;C—管壁粗糙系数,其值依据管材的不同而不同,本算例中C=140。
2.2 调压阀节点方程
采用矩阵法计算调压阀压力及流量,对阀门进出口断面的节点编号分别为1和2,反应调压阀进出口压力及过流特性的公式如下[14]:
QP1=QP2=QP
(5)
(6)
式中,QP—调压阀流量;τ—调压阀开度;f(τ)—调压阀开度的非线性函数;Dx—调压阀直径;HP1、HP2—节点1、2处的水头。
将公式(5)—(6)与特征相容方程联立求解,可得阀门流量方程:
(7)
将求得的QP反代入式(6)中,可求出减压阀进出口断面的水头HP1、HP2。
3 案例分析
3.1 工程基本资料
新疆某县供水管道由于建设年份久远,建设标准低等原因导致管道出现较严重的老化破损、跑冒滴漏现象,且随着该县人口的不断增长,用水量日益增加,原供水管网在压力设计方面均不能满足现阶段要求,为满足城乡供水需求,供水管道亟待修整,需进行仿真模拟计算为工程设计提供依据。根据初步设计资料可知,本城乡饮水工程输水主干管从水源地总水厂至县城全长111.88km,水源地总水厂地面高程为1467.00m,县城水厂地面高程为1202.47m,落差为264.53m。供水管网引水设计流量为935.31L/s,由于管网布置及所需供水压力的不同,管径的要求也不尽相同,选择干管设计直径为DN1200~DN600之间。管道沿途通过21个乡镇,支管设计管径为DN600~DN200,管材选用外聚乙烯内环氧树脂复合钢管和PE管,管道承压标准最高不超过50m。该项目全线呈树状管网分布,共有21处分水,在各输水管道末端建立水厂或加压站,输水管均匀供水至调节池,由加压水厂向县、乡镇管网配水。基于EPANET软件建立的输水管网模型布置图如图1所示,由图1可知,该管网总节点数52个,两节点之间连接细线表示管道,1号节点类型为总水厂; 3号节点类型为管材系数变化点,该类型的点在管网中共计30个;45号节点类型为分水厂加压站,整个管网该类型节点共计21个。管道的设计压力即为由内压(外压)与温度构成的最苛刻条件下的压力,根据设计要求,在本案例中管道最大承压标准不应超过50m,最低承压标准不应产生负压(小于0m),以此作为管网管道压力设计调保依据进行数值模拟计算。
3.2 单设减压池方案分析
当整个供水管网未增设任何防护措施时,管网模型执行单时段计算结果如图2所示,管网中各节点运行畅通,水流可以顺利从1节点流向其他节点,各节点旁的数字代表节点处水压力的大小,由图中颜色深浅和符号显示可知,引水口的上游1—9节点多处压力不符合管道压力标准,8号节点出现负压,将其区域放大后得到图3(a),8节点的负压值为13.5m,实际工程中负压降低至10m时,管道内水体已经发生汽化,低于- 10m压力大小仅代表负压的严重程度,由此可知,在8号节点处可能会由于负压过大管道产生干瘪,该现象的发生会对管道造成巨大破坏。上游节点除了产生负压外,3、4号节点压力值分别为64.87、52.04m,压力偏大且超出管道的承压标准50m,此时管道内压力过大,可能存在爆管的危险。综上,在供水管网未增设任何防护措施时,管道内负压严重,正压超标,不能满足设计调节保证的要求,以上两种情况的出现都会对管网造成严重损坏,需要在此管网布置的基础上加设其他防护措施以保证供水管网的安全运行。
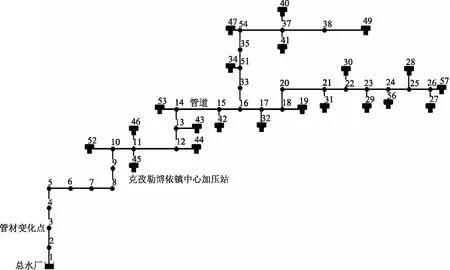
图1 模型管网布置图

图2 模型管网压力显示图
为了防止供水管网发生危险,基于原管网布置的基础上,在干管沿线8号节点处(产生负压处)增设一个一级圆柱型减压池对管道压力进行削弱,减压池直径为50m,初始水位设定为5.4m,最高水位限定20m。增设减压池后对管网进行数值模拟,计算结果如图3(b)所示。由图3(b)可知,经过减压池的降压,节点8的水压力得到了较好的改善,从原来的负压-13.65m变为了5.4m,管道整体无负压产生,减压池的增设很好地解决了管道负压问题。由上述计算说明,若管网运行存在负压,可在负压严重位置设置减压池,此措施可消除管网的负压,使管道内水流不会产生汽化。虽然增设减压池解决了管道的负压问题,但其他节点不但没有因设置减压池后压力发生下降,反而压力都有了不同程度上的增大,如5号节点压力由30.93m增大到44.69m,压力上升13.76m,7号节点由8.57m增大到24.47m,压力上升15.9m。分析原因是未设减压池时节点8处是负压,而当此处增设减压池后,此处压力升到5.4m,上游管段对节点8所需提供的压力增大,导致上游节点自身压力提高;节点8水位升高后,对下游节点的水压力也升高,致使节点9压力值也变大,所以减压池的增设提高了1—9节点的压力值。由图3还可看出,3、4号节点的压力值分别达到68.61、61.7m,已超出承压要求十余米,此时仅布置减压池已无法满足调保需求,管道仍存在爆管的危险,因此还需在管网其他位置布置其他减压措施以降低管道的压力极值。

图3 有无减压池模型结果对比图
单设减压池方案:管网无调压设施时,部分管段处的压力超出管道的承压标准,且产生较大负压,此时需要在负压管段处增设减压池以减小管道负压,保证管网安全运行。减压池的添加对管网负压的消除具有较大作用,但对管段中的超压现象未起作用,仅布置减压池已无法满足调保需求,管道仍存在爆管的危险,因此,在管网加设减压池的基础上还需要布置调压阀等减压设备以降低管段的压力极值。
3.3 池阀联合方案分析
本供水管网工程单独设置减压池并不能满足要求,根据管网布置条件,初步选择在管网中增设调压阀进一步降低各节点的压力大小,即减压池和减压阀联合降压,以保证输水管网的安全运行。EPANET数值模拟软件中调压阀的类型主要有6种,分别为:稳压阀(PSV)、压力制动阀(PBV)、流量控制阀(FCV)、节流控制阀(TCV)、常规阀门(GPV)、减压阀(PRV)。若将以上不同种类的阀门全部代入管网模型进行数值模拟计算,模拟次数过多、所需时间过长。为减少数值模拟的工作量,首先根据阀门用途和功能进行初步筛选。本模型主要针对有压管网压力大小进行调节,流量控制阀(FCV)和节流控制阀(TCV)只具备流量控制调节功能;不具备压力调节功能,压力制动阀(PBV)是迫使阀门处发生特定的压力损失,仅适合理想的模拟状态,不能运用于实际工程中;常规阀门(GPV)适用于模拟流速较大的紊流流态,水头损失不易求得。综上,以上4种阀门不适合本管网模型,故不选取。因此,本管网可选用减压阀(PRV)和稳压阀(PSV)对压力过大管道进行降压。稳压阀(PSV)主要维护管网特定位置的压力设置,阀门处于活跃状态,下游压力低于设置值时,在其上游侧维护该压力设置值;减压阀(PRV)主要限制管网特定位置的压力,阀门处于活跃状态时,当上游压力高于设置时,使其下游侧达到压力设置状态,二者工作原理不同。首先在压力过大的1—8节点之间增设阀门,通过穷举法对不同阀门数量及安装位置进行仿真计算,首先确定阀门安装数量与安装位置。根据计算结果可知阀门的最佳安装个数为2个,安装位置在节点2—3及3—4之间的管段中。
根据穷举法进行不同方案的数值模拟计算并确定最优阀门个数及位置后,得到最终调压阀布置图如图4所示,由图4可知,1#、2#调压阀分别安装在节点3、4处,根据本管网调压阀的启闭规律及管网管径、压力的要求,设定两调压阀的直径均为0.8m,1#调压阀的设置值为47m,2#阀门设置值为45m。该布置图中仅确定了管网调压阀的个数与最佳安装位置,并未确定调压阀的类型,根据在2个位置布置2种不同阀门共计存在以下4种方案进行模拟计算,不同方案阀门布置见表1。

图4 调压阀布置位置示意图

表1 不同方案阀门布置表
将表1中的4种不同方案分别用管网模型进行模拟,选取了2—8节点的管段为研究对象,为方便将减压阀和减压池联合降压的结果与单独设置减压池方案数据进行对比,将不同方案得到的各节点的压力值绘制于图5中,其中单独设置减压池的方案为方案0。从图5中可知,方案共有5个,图中方案0、1、3的这三个方案下压力变化曲线发生重合,表明方案1(双PSV)及方案3(1#PSV、2#PRV)设置减压阀并没有使管道压力减小,方案1、3的压力变化与未设置减压阀仅设置减压池方案的压力变化一致,说明方案1、3设置减压阀并未起到任何减压效果,方案设计失败。原因是方案1、3处的1#调压阀均是稳压阀(PSV),该阀门特性是将阀门两侧的压力稳定在固定值,由于该阀的设置使方案1中1#稳压阀(PSV)和3中2#减压阀(PRV)处于全开状态,失去了减压的作用,故管网仍维持原先压力保持不变,未起到降压效果。从图中还可看出,方案2、4中各节点压力相较于仅设置减压阀方案0有了较大减压效果。方案2(1#PRV、2#PSV)中节点3的压力从68.61m降低至47m,节点4的压力由61.7m降到了48.45m,其他节点均发生了不同幅度的减小,因其阀门的布置方式减压幅度较小,降压效果不显著。方案4(双PRV)节点3由原来压力值68.61m 降低至47m,节点4的压力由61.7m降到45m,其他节点处压力也均有不同幅度的降低。对比方案2、4,以上两种方案均使管道压力发生较大降幅,各节点压力均能满足管道的承压标准,虽然方案2、4各节点压力变化趋势基本一致,但部分节点压力值不太相同,主要体现在节点4、5、6处,原因是方案4中的双PRV阀门都处于活动状态,即阀门开度0 图5 不同调压阀方案各节点压力变化 池阀联调方案:在调压阀类别、个数及布置位置的选择上先运用穷举法判断调压阀的最佳安装数量及位置,之后进行类别的确定。将不同类别的调压阀配置方案分别进行数值模拟计算,通过对计算结果进行比选,选择出降压效果最好的调压阀配置方案。 本文基于供水管网的基本理论,通过EPANET软件分别建立了单独设置减压池和减压池、调压阀同时设置的供水管网的数学模型,模拟了某实际工程有压管网输水工程的运行过程,计算了供水管网不同管段压力变化。通过将池阀联调方案与单独设置减压池方案的仿真计算结果进行对比,可知该供水管网中单设减压池无法满足调保需求,管道仍存在爆管的危险;池阀联调方案的布设,不仅可以保证负压的有效排除,也可使管网所有管段压力均满足承压标准,进而保障了供水管网的运行通畅与安全,则池阀联调方案可作为实际工程的推荐方案。
4 结论

