数字化主动配电网的多谐波源谐波责任划分方法

李树荣,马晓燕,李 华,陈长金,李伟豪

(1.国网河北省电力有限公司雄安新区供电公司,河北 雄安新区 071000;2.天津大学电气自动化与信息工程学院,天津 300072;3.国网河北省电力有限公司涉县供电分公司,河北 邯郸 056000;4.国网河北省电力有限公司电力培训中心,河北 石家庄 050021)

随着电网的不断发展和低碳发展理念的普及,太阳能、风能等分布式电源作为清洁能源大量接入电网,导致传统电网的源荷关系发生了显著变化。为维持电网安全稳定、经济高效运行,电网控制由被动发展为主动,“主动电网”概念应运而生。与此同时,信息革命也在悄然发生,数字化作为信息革命的重要特征,其对电网的影响不可忽视,数字化主动配电网在能源网架、信息支撑和价值创造方面对传统电网赋能,实现业务数字化,数字价值化。数字化主动配电网中大量并网逆变器和控制系统接入电网,由此产生的谐波污染问题引起广泛关注[1-2]。非线性负荷和电力电子设备注入电网的谐波电流,不仅会使电网和负荷增加损耗,还会造成局部过热加速老化,缩短使用寿命等负面影响[3],因此为有效治理谐波污染,改善电能质量,需要准确划分PCC处各谐波源的谐波污染责任,进行有效治理。

1 多谐波源责任划分方法概述

目前国内外在谐波责任划分领域有“干预式”[4-7]和“非干预式”两类方法。“干预式”方法由于需要向系统中人为注入谐波扰动,因而容易对系统造成不利影响,采用较少。较为常用的“非干预式”方法又可以分为参考阻抗法[8]和数据分析法,当前研究主要集中在数据分析法,很多研究者做出了有益探索。文献[9]提出波动量法,利用PCC电压电流波动量比值估算谐波阻抗,进而划分谐波污染责任,但是精度无法保证,而且主导侧不能判定。文献[10]提出线性回归法,根据诺顿等效电路方程系数来计算系统侧谐波阻抗和背景谐波,进行谐波责任划分,但是当背景谐波非正态分布时,估计有偏,而且易受不良数据干扰。文献[11]提出了随机独立矢量法,利用独立随机矢量协方差为零来提取系统侧谐波阻抗,划分谐波责任,但是当系统侧谐波发射水平较高时,误差较大,结果不够精确。文献[12]提出了极大似然估计法,其模型建立在背景谐波正态分布的基础上,求解似然方程得到系统侧谐波阻抗值,计算谐波责任,然而实际系统中,非线性负荷停机时的测量背景谐波难以符合标准正态分布的假设。

独立分量分析(Independent Component A-nalysis,ICA)是近年发展起来的一种新的盲源分离技术,利用源信号的独立性或弱相关性对混合信号进行解混分离。其中快速独立分量分析法(FastICA)由于无需选择步长,收敛速度快等优点而最为常用,国内外已有学者将该方法应用到谐波污染责任划分问题上[13],取得了比较理想的效果,但只针对单谐波源的谐波责任划分。

为将FastICA推广到多谐波源谐波责任划分领域,本文提出了基于FastICA的多谐波源谐波责任划分方法,利用PMU测量得到的同步电压电流数据经过FFT得到各次谐波数据。然后将各次谐波数据拆分为实部虚部(x-y)分量,分别代入多谐波源等效混合模型,由FastICA解混分离出各源信号和混合矩阵计算得出谐波阻抗和背景谐波,最后在PCC处谐波电压上投影得到各谐波源的谐波污染责任。

2 基于FastICA的多谐波源谐波污染责任划分方法

2.1 快速独立分量分析

目前解决盲源分离(Blind Source Separation,BSS)问题最常用的是ICA技术,其无需先验知识,只需要各源信号相互独立或存在弱相关性即可,而且其消除噪声性能佳,在消除噪声的同时,可以有效分离各源信号,对其他细节几乎无破坏。

ICA分析的数学模型为:

式中:t为离散时刻,取值为t=1,2,… ,tn;S(t)为N个未知的源信号组成的矩阵,S(t)=[S1(t),S2(t),…,SN(t)]T;X(t)为M个可观测信号组成的矩阵,X(t)=[X1(t),X2(t),…,XM(t)]T。

ICA建立在以下基本假设前提下:

a.各源信号Si(t)均值为0并为实随机变量,源信号之间统计独立;

b.源信号数N小于等于混合观测信号数M,即M≥N;

c.各源信号Si(t)至多有1个高斯信号,即至多有1个源信号的概率密度函数为正态分布。

FastICA算法采用牛顿迭代算法对数据进行处理,具有收敛速度快、分离效果好、迭代稳定、无步长参数、易于使用等优点,使之在ICA算法中应用较为广泛,因此,本文采用FastICA算法进行盲源分离。

FastICA算法以负熵作为衡量信号独立性的目标函数,采用近似负熵作为度量随机变量非高斯性的判据,负熵越大则其非高斯性越强。本文采用的FastICA算法的目标函数是一种基于最大熵原理的负熵近似计算法,其数学表达式如下:

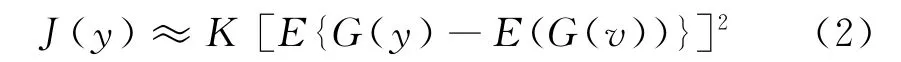
式中:K是一个正常数,y、v是均值为0,方差为1的随机变量。G是一个非二次函数,这里采用如下所示的函数代替:

FastICA优化算法的实质是通过寻求使J(y)取得最大值的分离矩阵W,求出对应的估计结果Y。由于现实中的源信号之间不可能总是完全相互独立,因此在进行盲信号处理之前要对混合信号做预处理,分为2步:第1步是去均值,避免数据量纲相差过大引起误差;第2步是白化,去除混合信号之间的相关性,减少迭代次数提高算法稳定性。去均值的公式为:

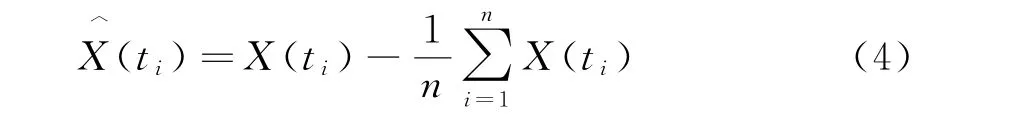
式中:n为各观测信号的数据长度,取值应当适宜,若数据长度过大会增加计算量,每次计算时间跨度大,期间系统谐波容易变化;若数据长度过小则分离效果不佳,导致谐波污染责任划分有误。

白化处理是线性变换,有:

式中:W0为白化矩阵,其公式为W0=Λ-0.5U T,Λ为协方差矩阵的特征值矩阵,U为C X的特征向量矩阵。

经过上述处理过程后即可进行迭代分离,迭代的目的是使负熵最大化,通过对负熵最大近似值E{G(W TZ)}优化求得。经过公式推导可得优化后的牛顿迭代算法:

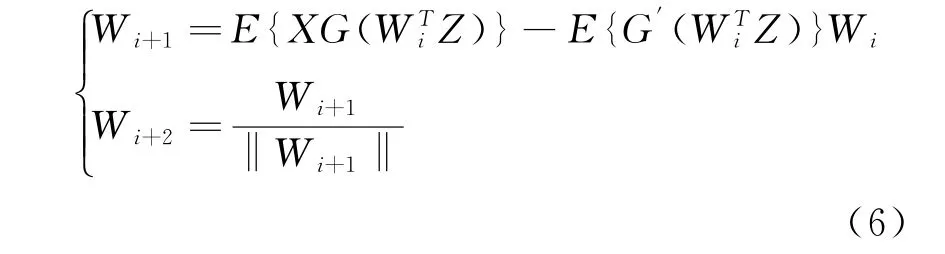
式中:i=1,2,…,m,m表示迭代次数。当‖Wi+1‖没有变化或者变化小于给定值时,迭代完成。此时Y为最终分离的独立分量。

综上所述,求解步骤如图1所示。

图1 FastICA求解步骤

2.2 基于FastICA的多谐波源谐波责任划分

配电网中多谐波源的谐波污染问题可以用图2表示。

图2 配电网谐波污染

图2中PCC处的谐波电压是系统侧背景谐波和多个谐波源负荷共同作用的结果。配电网中谐波源负荷向电网中注入谐波电流,流经系统谐波阻抗,增强了PCC处的谐波电压,PCC处谐波电压可由下式计算:

式中:V hpcc是PCC处h次谐波电压,I h1,I h2,I h3,I h4是谐波源负荷1、谐波源负荷2、谐波源负荷3和谐波源负荷4的h次谐波电流,Z h1pcc,Z h2pcc,Z h3pcc,Z h4pcc分别是谐波源负荷1、2、3、4与PCC之间的h次谐波传递阻抗,V h0是h次背景谐波。V hpcc是各谐波源负荷混合作用的结果,可以等效看作FastICA模型中的混合信号,由此根据ICA数学模型建立谐波污染等效模型,如公式(8):

式中:V hpcc=[V hpcc(t1),…,V hpcc(t n)]是PCC处h次谐波电压各时刻采样值向量,I h1=[I h1(t1),…,I h1(t n)],I h2=[I h2(t1),…,I h2(t n)],I h3=[I h3(t1),…,I h3(t n)] 和I h4=[I h4(t1),…,I h4(t n)]分别是谐波源负荷1、谐波源负荷2、谐波源负荷3和谐波源负荷4的h次谐波电流各时刻采样值向量。由于FastICA分离结果具有幅值和次序的不确定性,因此为解决幅值不确定性,可推导得式(9):

式中:I h1-Y,I h2-Y,I h3-Y,I h4-Y和V h0-Y是FastICA分离结果,通过k1,k2,k3,k4的不同取值即可解决FastICA分离结果的幅值不确定性,次序不确定性可以通过分离结果与源信号的相关系数匹配解决,相关系数定义如下:

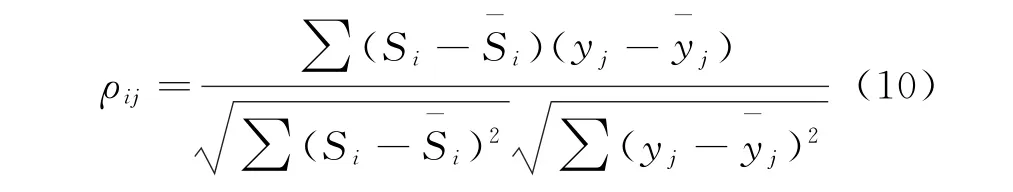
由于越相似其相关系数越大,因此当ρij绝对值接近于1时,可以认为源信号S i与分离信号y i相匹配,即分离信号y i是源信号S i的对应分离结果。由式(9)可得谐波传递阻抗如下:

Z h2pcc,Z h3pcc,Z h4pcc同理可得。

下面计算谐波污染责任,如图3所示。

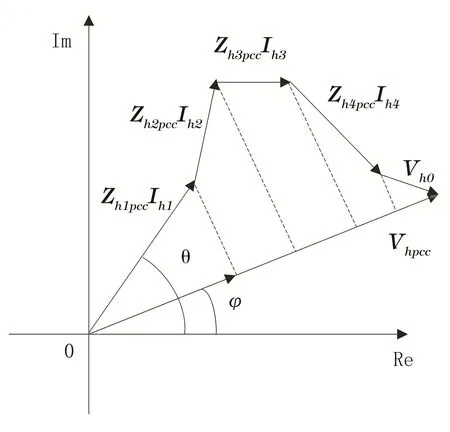
图3 谐波污染责任计算

各谐波源h次谐波污染责任可由其在PCC处产生的谐波电压在V hpcc上的投影与的比值计算得到,计算公式为:

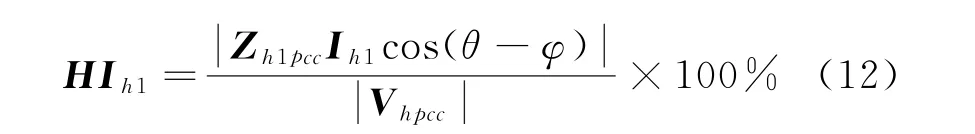
式中:HI h1为谐波源负荷1在PCC处h次谐波污染责任;θ为谐波源负荷1的谐波电流在PCC处引起谐波电压Z h1pcc I h1的相角;φ为PCC处h次谐波电压V hpcc的相角。

综上所述,基于FastICA的谐波责任划分步骤如图4所示。

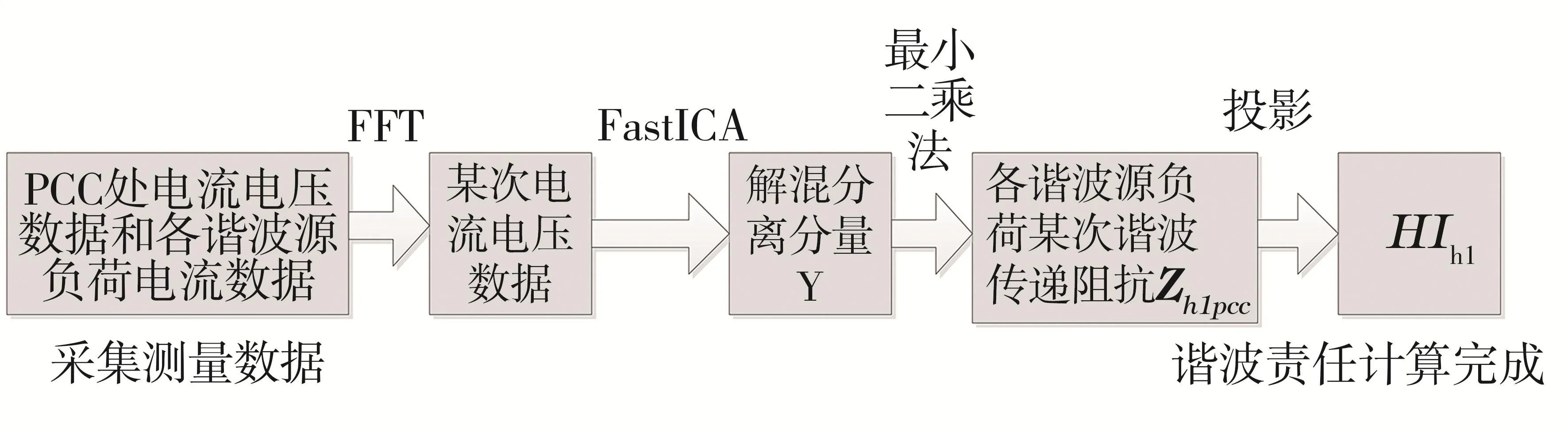
图4 计算步骤示意

3 仿真分析

为验证上述方法的正确性,采用MATLAB/simulink平台搭建了18节点的10 k V配电网模型。拓扑结构如图5所示。

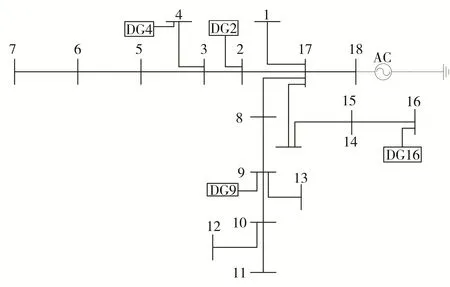
图5 配电网拓扑结构

在节点2、4、9、16分别接入DG,DG接入处和PCC处均已安装电流电压量测装置。采用的DG模型为恒流源模型,参考并网逆变器典型谐波频谱设置参数(见表1)。仿真时将谐波源负荷在90%～110%额定值范围内随机波动,模拟实际系统中负荷的自然波动。

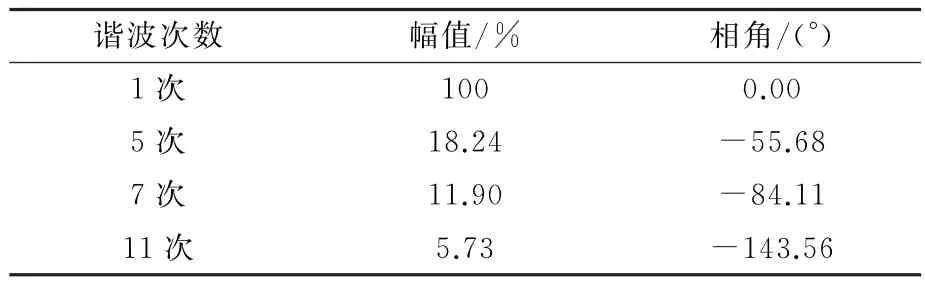
表1 谐波源负荷的谐波电流典型频谱

首先,通过simulink仿真得到电流电压量测数据,采样频率为12 800 Hz,数据长度为256个点。利用FFT得出所求某次谐波电流电压数据,以5次谐波电流电压为例,得PCC处5次谐波电压和各谐波源负荷5次谐波电流如图6所示。

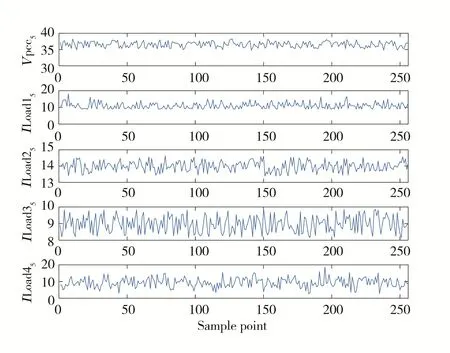
图6 5次谐波电压电流值

由于FastICA要求输入信号为实随机变量,因此在输入FastICA程序前将数据拆分为实部虚部分别进行FastICA计算。分离效果如图7、图8所示。

由图7、图8不难辨识混合信号与源信号对应关系,解出混合矩阵A,进而由式(11)求得各谐波源负荷到PCC处的谐波传递阻抗,最后由式(12)求得各谐波源在PCC处的谐波责任。计算结果(取256次均值)如表2所示。

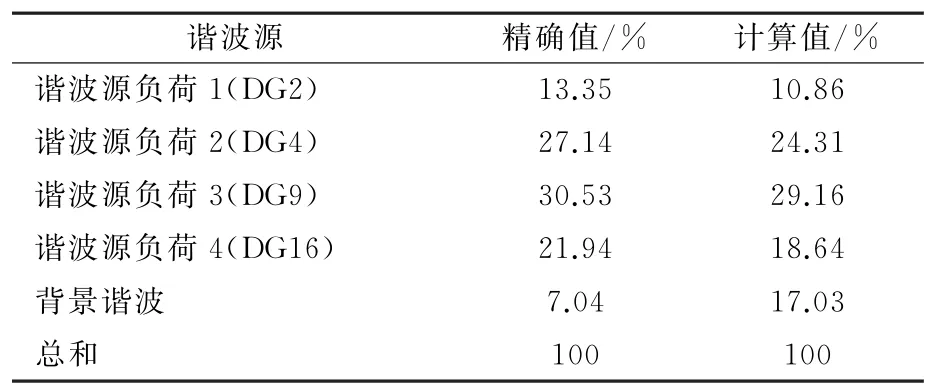
表2 谐波责任计算结果

由表2数据可以看出,该方法谐波责任划分的精度较高,具有实际应用价值。

4 结束语

本文提出的基于FastICA的多谐波源谐波责任划分方法,通过采集数字化主动电网中布置的PMU测得的同步电压电流数据经过FFT得到各次谐波数据;然后将各次谐波数据拆分为实部虚部(x-y)分量,分别代入多谐波源等效混合模型,由FastICA解混分离出各源信号和混合矩阵计算得出谐波阻抗和背景谐波;最后在PCC处谐波电压上投影得到各谐波源的谐波污染责任,实现准确划分多谐波源谐波污染责任的目的。

数字化主动配电网中各类传感器密集布置,数据越来越多元,比如热信号、光信号、振动信号等,如何利用多种数据,实现多角度监测谐波,需要在之后的工作中进一步探索。