二连杆机械臂的重复性滑模控制
赵逸吉
(延锋安道拓座椅有限公司,上海201315)
1 项目概述
本文的控制对象是一个二连杆机器人,如图1所示,目标是使其末端器(end effector)跟踪一条周期性的期望路径,误差尽可能小。

图1 控制对象的实物图与示意图
两个Maxon EC电机用于分别控制两杆,正交编码器记录脉冲数,同时计算转动的角度。由于存在摩擦、重力力矩变化,尤其还有因齿隙(backlash)等装配误差,该控制对象是一个非线性较强的二阶系统。为使其精确受控,拟采用重复控制(RC)。
重复控制最初在20世纪80年代被提出[1],是基于内模原理的控制方法,能有效抑制周期性干扰并达到高精度控制,因此受到广泛的关注。近期仍有许多学者对此进行研究,如LinLin Li等人将其应用在纳米定位器上[2];Lennart Blanken等人设计组合了多个重复控制器以达到更高精度且快速收敛的目的[3];Hassan Farokhi Moghadam等人使用自适应快速傅里叶变换(AFFT)来辅助重复控制得到干扰的精准周期[4]。
然而,应用重复控制需要上个周期的系统信息。故控制伊始,先采用滑模控制(SMC),几个周期后,采用基于SMC修改的重复控制律。
2 相关假设
2.1 齿隙干扰
电机的转角为编码器计数而得,但由于齿隙的存在,实际情况会有误差。为消除此误差,一般会建立反向齿隙模型,如Chunyi Su等人提出的连续时间动态模型[5]。
然而,由于难以构筑精确的反向齿隙模型,将其应用在控制算法里容易导致失稳。这是因为在机械臂改向时,电机的转角大小会有一个跳变。故本文将齿隙归为了干扰的一部分,试图通过控制算法来尽可能降低齿隙的影响,同时也成为了衡量控制方法抗干扰性的一条指标。
2.2 摩擦识别
根据实验数据,本文选取所应用电机的摩擦模型,为库仑及粘性摩擦的组合。摩擦识别如图2所示。
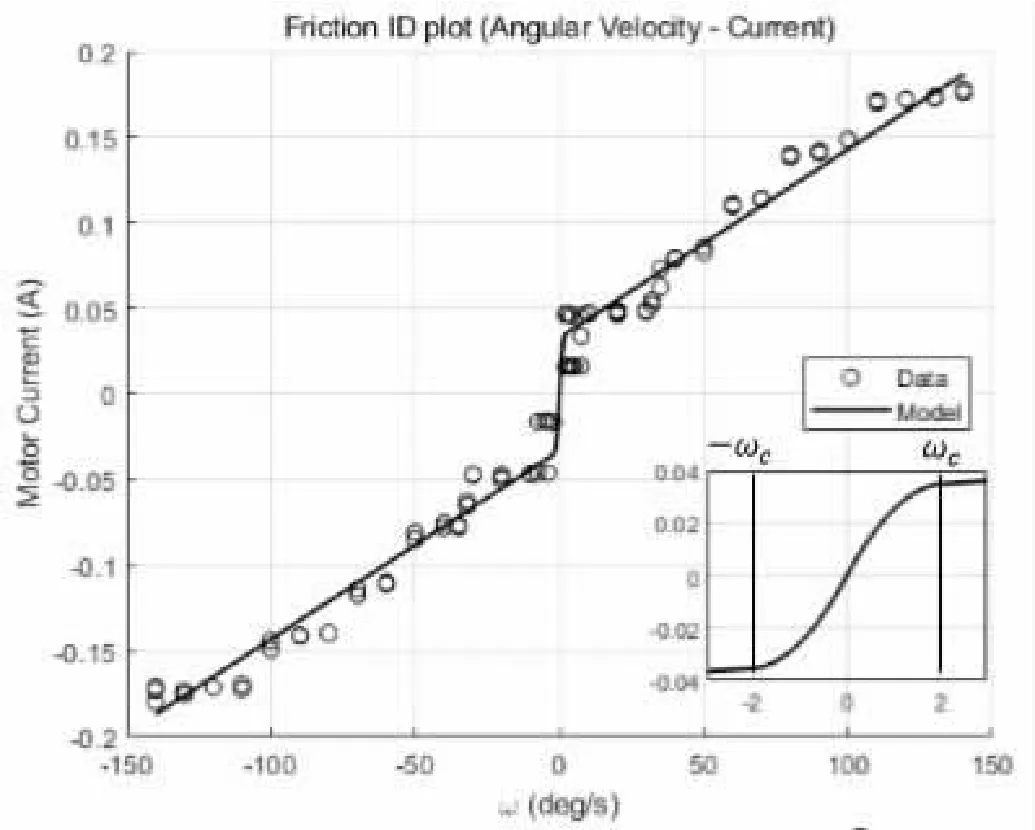
图2 电机摩擦模型
由此,电机电流与角速度的关系被拟合,并将其转化为摩擦力矩与角速度的关系,总结成如下的关系式:
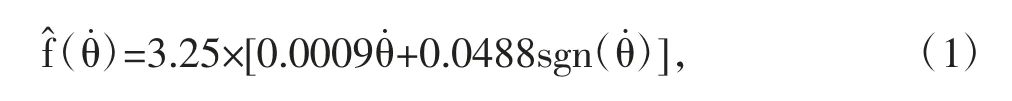

式(2)是应用本文所述控制方法的前提,允许摩擦力矩估计值与真实值有一定程度的偏差,此偏差上限F需根据实验数据合理设置。
3 控制方法
本节介绍控制方法的具体内容。总体步骤为:(1)建立系统的数学模型。(2)根据模型求取系统总动能与总势能。(3)解拉格朗日方程得到运动方程。(4)在一种适合于非线性系统的自适应鲁棒控制律的基础上,融入重复控制思想,形成本文所提议的控制律。
由于控制对象的几何参数一定,末端器的位置可由两杆转角确定。故末端器的周期性期望路径,亦可转化为两个转角的周期性期望路径。
如图3建立坐标系,设杆长是l1和l2,质量是m1和m2。两杆质心到转轴的距离为r1和r2,而两质心坐标为:(正余弦简写,如sinθ1与cosθ2简写为s1与c2)
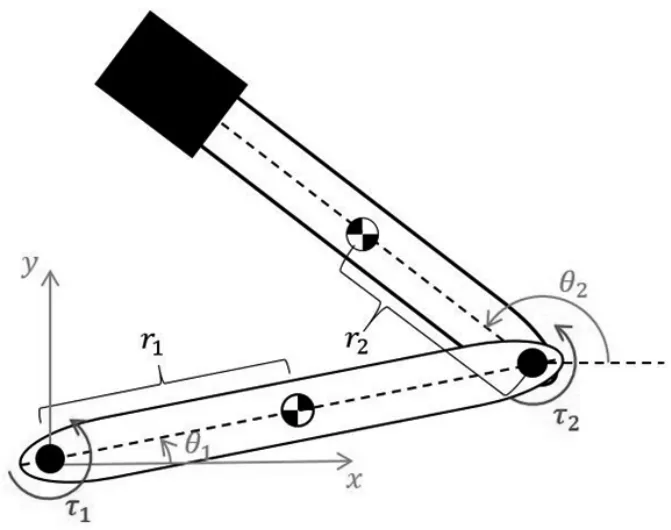
图3 建模示意图

对式(3)求一阶导后得:
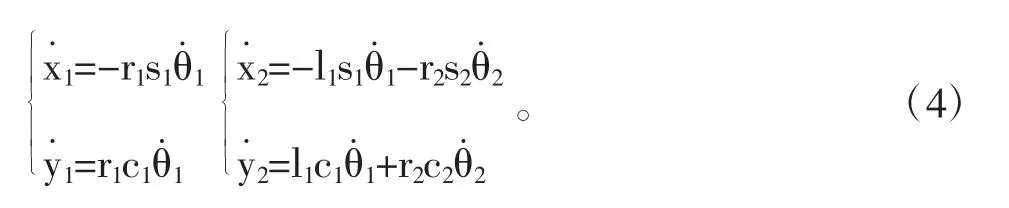
由上式所得速度求取系统总动能得:
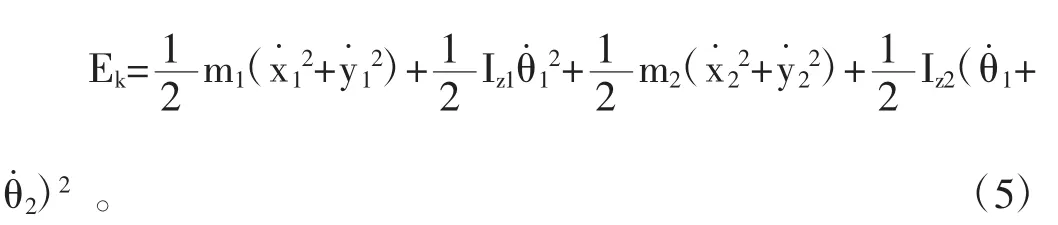
其中Iz1与Iz2为两杆在质心处的转动惯量。将式(3)和(4)代入(5)经化简得:
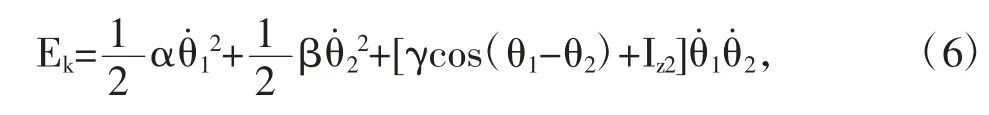
其中:

注意到α、β、γ皆为常数,故系统总动能仅由其姿态(两转角之差)及转速决定。而系统总势能为:

得到总动能与总势能后,即可计算拉格朗日函数:

将其代入拉格朗日方程:

由式(10)可导出系统的运动方程,经整理即可写成如下形式:
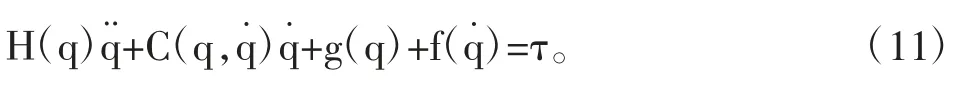
其中q=[θ1θ2]T,τ=[τ1τ2]T,且H、C、g三个矩阵分别为:
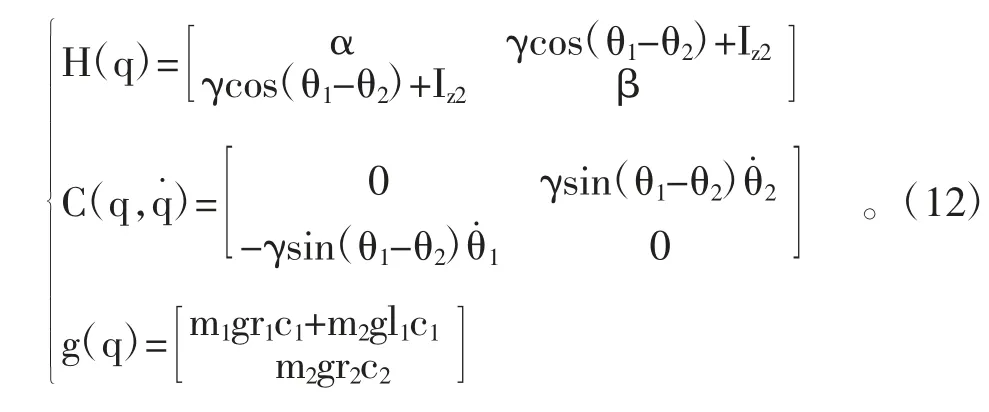
注意到式(11)一开始是不含有摩擦项f(q˙)的,而是在推出运动方程后补加进去的。事实上,从式(6)可以直接导出H(q),因为动能并且,C(q,q˙)中的每一项,也就是Ckj,皆可用H(q)经由克氏符(Christoffel symbols)计算而得:
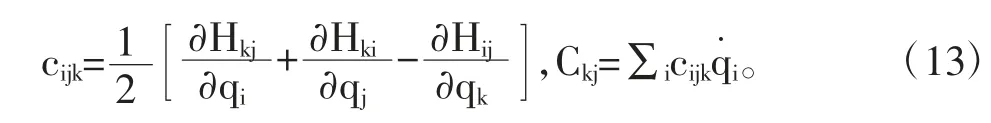
针对式(11)形式的运动方程,如Slotine教授所述[6],一种自适应鲁棒控制律(滑模控制)如下:
通过构筑合适的李雅普诺夫函数(Lyapunov function)可证明式(14)的稳定性及鲁棒性[6]。K的取值也在此过程中确定,其涵盖了式(2)中的摩擦力矩偏差上限F。针对本文中的系统,Y与a如下:
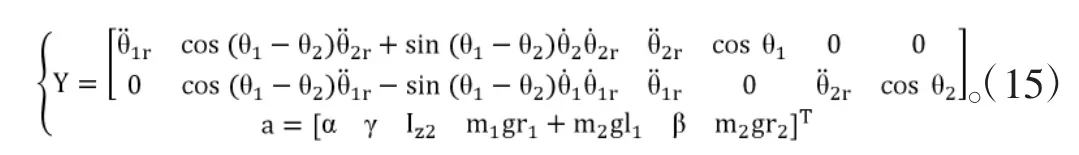
在应用式(14)所示的自适应鲁棒控制律控制系统几个周期后,即可应用本文所提议的重复控制律:

重复控制有多种形式,比如可以配合扰动观测器(Disturbance observer)使用,而上式是其中一种经尝试简明有效的控制律。其中,i代表每个迭代(iteration),N为一周期内迭代次数,Q是一个低通滤波器,C是需要被调试的常数(正值)对角矩阵。滤波器在重复控制中是极其必要的,否则扰动将使系统不可控,在每个周期都发生叠加,愈演愈烈。
4 实验设置
如图4所示,MaxonEC电机驱动模块、NImyRIO开发板、电源发生器,是实现机械臂控制的主要设备。在此基础上,编写LabVIEW FPGA代码来实施前述的控制方法。

图4 重复性滑模控制实验结果
首先在软件中建模,系统的传递函数可由输入输出的测试数据建立。接着是控制仿真,在此过程中,调试λ、C等参数,使跟踪精度更高。成功后,就将其应用于现实系统。
5 实验结果
为提供重复控制所需的过往周期数据,并直观地进行对比,滑模控制(SMC)首先应用于两关节(joint),过50秒(5个周期)、100秒(10个周期)后,先后在两关节上应用本文提议的控制律。
所用各参数为λ1=λ2=2,C1=2,C2=1.5,转角跟踪曲线皆为tanh(2sin(0.2πkT))的拉伸与平移,实验结果如图5所示。
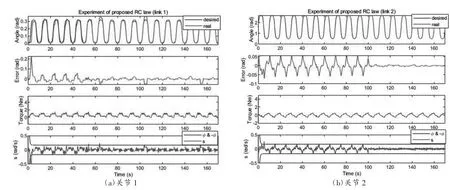
图5 重复性滑模控制实验结果
5个周期后,提议的控制律应用在关节1处,可看到θ1的跟踪表现有所提高,几个周期内的误差绝对值平均为0.007rad。虽然某时会有相对较大的误差,但整体表现证明了它的有效性。
10个周期后,提议的控制律应用在关节2处,很明显θ2的误差等级大大下降,几个周期内的误差绝对值平均仅为0.00205rad。并且,s的值非常接近0(误差及误差导数小)。
更仔细地调试参数后,实验表现应可进一步提高。然而,本文所侧重的是证明所提议控制律的可行性及实用性,目前的实验结果也已达此目的。
6 结论
本文提议的重复性滑模控制,有着取自重复控制及滑模控制的优势:非线性系统的控制器易于设计,也不需知晓精确的系统参数;重复控制律进一步提高跟踪精度。实验中的表现也十分良好,且系统参数的不确定性、摩擦、齿隙等干扰所带来的影响被大大减弱。故其具有较强的实用性。
有关所提议控制方法的局限性,主要是以下几点:如其他大多数控制方法一样,普适性会有欠缺,且此控制律是基于重复控制的思想,故也仅适用于跟踪周期性期望路径;在高阶或其他有着更强非线性的系统前,可能作用有限。

