一种基于UWB TDOA定位模式的迭代最小二乘算法

何成文 袁运斌 潭冰峰

1 中国科学院精密测量科学与技术创新研究院大地测量与地球动力学国家重点实验室，武汉市徐东大街340号，430077 2 中国科学院大学，北京市玉泉路19号甲，100049

对TDOA定位模式下的LOS信号场景的算法研究很多[1-14]，包括两步加权最小二乘(two-step weighted least squares，TSWLS)算法[1]、线性修正最小二乘(linear-correction least-squares，LCLS)算法[2]、约束加权最小二乘(constrained weighted least squares，CWLS)算法[3-4]、分离约束加权最小二乘(separated CWLS，SCWLS)算法[5]和迭代约束加权最小二乘(iterative CWLS，ICWLS)算法[6]等。但这些方法难以同时兼顾精度和抗噪性能。为此，本文提出一种简单有效的非约束迭代优化算法，并用实验验证其效果。

1 算法描述

结合室内定位的特点，考虑采用N个UWB基准站去定位UWB标签的2维坐标。假设si=[xi,yi]T为已知UWB基站坐标，u0=[x,y]T为待求标签位置，通常选择第1个基站作为参考站，则常规TDOA-LOS定位方程为：

(1)

式中，di,1为标签到第i个基站和到第1个基站之间的距离差，ηi为均值为0的高斯白噪声。对式(1)移项后进行平方展开，忽略高斯白噪声的影响，可将其转化为线性形式Gu1=h，其中，

(2)

u1=[x,y,R]T

(3)

(4)

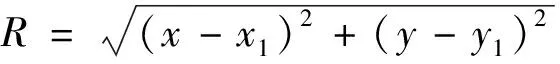
由于R与u0和s1之间存在如下关系：

R2=(u0-s1)T(u0-s1)

(5)

因此，传统CWLS算法[3-5]的表达形式可写为：

min(h-Gu1)TW(h-Gu1)

s.t.R2=(u0-s1)T(u0-s1)

(6)

式中，W为加权矩阵。

CWLS算法已有较为快速的解法，但在定位精度方面仍存在较大的提升空间。为进一步提高CWLS算法的定位精度和运算速度，并解决约束方程的非凸问题，Qu等[6]提出迭代约束加权最小二乘(ICWLS)算法。该算法通过新的等式变换，将具有非凸特性的CWLS算法表达式转化成具有凸性的新表达式。尽管仿真实验证实了该算法的有效性，但在大噪声环境下却存在定位发散的缺点。

为解决定位发散的问题，本文提出一种简单且适用于大噪声环境下的TDOA定位算法。首先假设基准站坐标位于笛卡尔坐标系原点(即便真实场景中基准站坐标不在原点，也可通过坐标变换来实现)，因此，式(1)可被重新写为：

(7)

通常在室内环境中，观测值不会很大且白噪声较小，而白噪声的分析常用于计算加权矩阵，由于本文算法不属于加权类算法，因此可忽略式(7)中噪声项的影响。利用勾股定理，可将式(7)转化为：

(di,1+R)2=(x-xi)2+(y-yi)2

(8)

展开移项后可得到：

(9)

令

(10)

(11)

(12)

则式(9)可写为如下线性形式：

2AR=C-2BX*

(13)

(14)

(15)

当式(15)多次迭代后达到式(16)的迭代停止准则时，即可停止迭代，从而输出最终定位结果：

(16)

式中，ε为误差阈值，数值一般比较小。

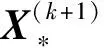
(17)

通常初值可以由最小二乘算法得到，而最小二乘解是无偏的，因此式(17)中每步迭代解的期望都等于最小二乘解，是无偏估计解。

2 仿真实验

通常情况下，室内环境相对复杂，视距条件下的基站总数相对有限。为保证UWB定位算法的可行性，仅采用4个UWB基站定位标签的位置，坐标分别为A1(0,0)、A2(10,0)、A3(10,10)和A4(0,10)，标签接收来自各个基站的信号中含有均值为0、方差为σ2的高斯白噪声ηi。由于本文的主要目的是评价算法在大噪声环境下的性能，故将噪声方差分别设置为0.1、0.25、0.5、0.75和1以进行综合评价，将每个噪声方差下的蒙特卡洛仿真实验次数和迭代阈值ε分别设置为2 000和0.000 01。

基于Qu等[6]的仿真实验结论可知，ICWLS算法的定位精度优于TSWLS算法、SDR算法、CWLS算法和迭代似然估计法，因此本文仅选择该算法与本文算法进行对比。在定位初值方面，2种算法均采用最小二乘解作为迭代初值；在精度评价指标方面，本文采用均方根误差(RMSE)来评估2种算法的性能，计算公式为：

2.1 实验1

为充分对比2种算法在边缘点和中心点处的定位精度，在LOS信号环境下选择近基站点L1(1, 1)和近中心点L2(5, 6)进行测试，2种算法在测试点处的定位精度见图1。由图可知，当噪声方差σ2≤0.25时，ICWLS算法的精度性能与本文算法大致相同。然而，当σ2>0.25时，ICWLS算法的性能误差开始急剧上升，而本文算法则缓慢上升，且误差低于ICWLS算法。因此，总体而言，本文算法在定位精度和抗噪声性能方面表现更好。

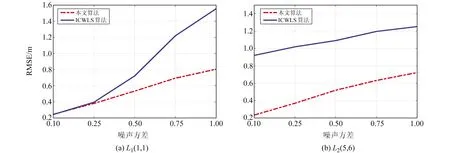
图1 2种算法在不同点处的定位精度

2.2 实验2

为进一步测试2种算法的定位精度，在4个基站围成的矩形区域中随机生成标签的位置，实验结果见图2。可以看出，本文算法显著优于ICWLS算法，在数值方面，本文算法的相应误差大约只有ICWLS算法的一半。此外，实验发现，本文算法迭代到收敛的平均迭代次数为15次。

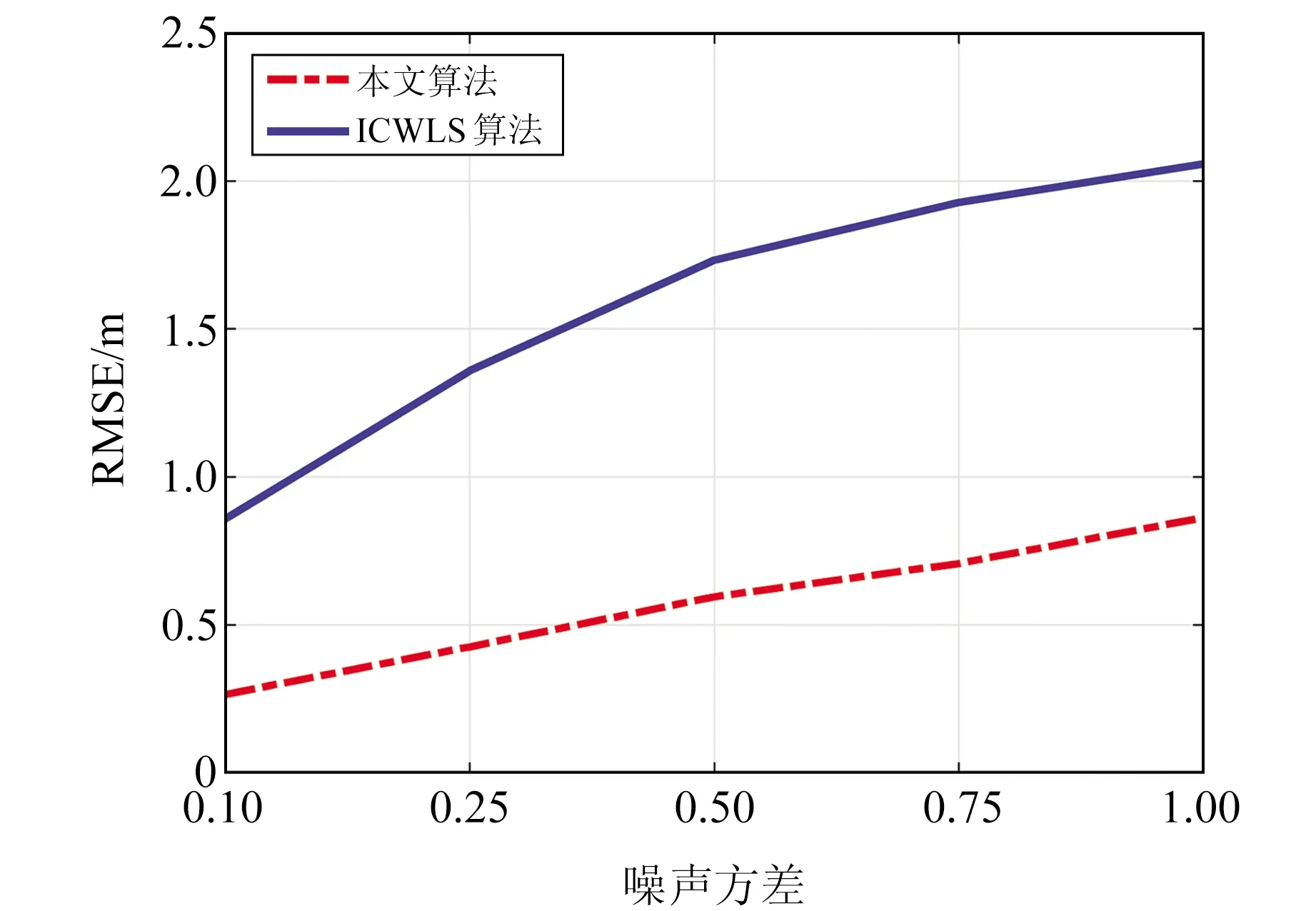
图2 2种算法在随机点环境下的定位精度

2.3 实验3

基于实验1和实验2的仿真结果，通过定位散点图来探究ICWLS算法定位性能较差的原因。将标签位置分别固定在L1(1,1)和L2(5,6)处，并将其噪声方差分别设为低噪声σ2=0.1和高噪声σ2=0.8，结果见图3。从图中可以看出，在低噪声条件下，2种算法的定位坐标基本分布在同一区域内，变化不大；在高噪声条件下，本文算法的定位结果接近真值，但ICWLS算法的定位结果分布在2个不同的区域，产生严重的发散。结合2种实验场景的定位结果认为，ICWLS算法存在一定的发散现象，这种发散现象在低噪声环境下不明显，在高噪声环境下相对明显，而本文提出的定位算法具有良好的收敛性和抗噪声性能。

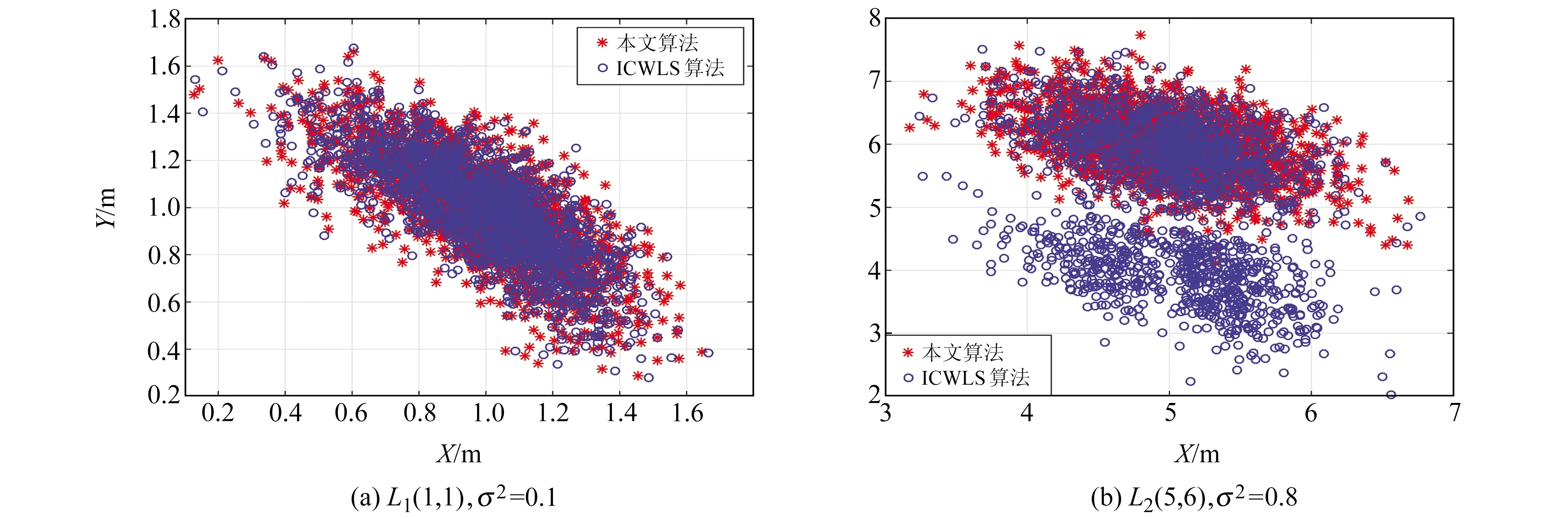
图3 2种算法在不同点处的定位坐标

由此认为：1)本文提出的算法优于ICWLS算法；2)无论噪声方差是多少，本文算法的定位结果都与真实位置更接近，说明本文算法具有良好的抗噪声性能；3)ICWLS算法存在定位发散的缺点，这可能是其定位性能不如本文算法的根本原因。

3 结 语

针对传统TDOA算法因抗噪性能弱而导致定位发散的缺点，本文提出一种简单的TDOA定位算法。该算法首先将TDOA定位方程转化为LS形式来得到初始解，然后通过迭代思想得到收敛坐标。本文算法原理简单、抗噪声性能好、易于实现，可推广到工业领域，且仿真结果也验证了本文算法具有可行性和有效性，定位精度优于ICWLS算法。