TMSR白光中子源能量分辨率函数的模拟研究

姜 炳，王小鹤，韩建龙,*，胡继峰，陈金根，蔡翔舟,*

(1.中国科学院 上海应用物理研究所，上海 201800；2.中国科学院 先进核能创新研究院，上海 201800；3.中国科学院大学，北京 100049)

白光中子源是中子束流能量分布较广的中子源。区别于单能中子源，白光中子源能提供跨多个量级的连续能量中子束流，是中子核数据测量必不可少的实验装置。国际上已建成的白光中子源主要分为两类：一类是散裂中子源，如欧洲核子中心(CERN)的n_TOF[1-2]和中国散裂中子源CSNS[3]等，这类中子源一般由质子加速器驱动，利用高能质子轰击重金属靶，发生散裂反应放出中子；另一类是电子直线加速器驱动的白光中子源，如美国橡树岭国家实验室的ORELA[4-5]，欧盟委员会联合研究中心设在比利时的GELINA[6]、韩国浦项的PNF[7]，以及中国科学院上海应用物理研究所自主设计的TMSR白光中子源(TMSR-PNS)[8]等，这类中子源是利用电子直线加速器产生的高能电子与重金属靶发生轫致辐射反应产生高能光子，光子继续与金属靶核发生(γ,n)反应放出中子。

在基于白光中子源开展的中子核数据测量实验中，测得的中子束流能量及其不确定度是决定实验数据质量的重要指标之一。白光中子源所产生的中子束流的能量通常使用飞行时间方法进行测量[9-10]，即通过测量中子飞行一定距离所用的时间(time of flight, TOF)来确定中子能量。由于白光中子源中子束流产生机理的限制，飞行时间谱仪所测中子的能量不确定度(能量分辨率)一般需通过蒙特卡罗模拟确定。

本文针对TMSR白光中子源，根据其结构及参数，采用Geant4程序，通过模拟特定慢化体条件下产生的中子束流在不同能区范围的飞行时间分布，研究给出能量分辨率随中子束流能量变化的函数关系。

1 实验装置

TMSR-PNS是国内首台专用于核数据测量的电子直线加速器驱动型白光中子源。TMSR-PNS布局如图1所示，其由电子直线加速器(LINAC)、中子产生靶系统(钨靶)、中子飞行时间谱仪(中子准直器、飞行管道和探测器)等部分组成。LINAC输出的电子束流能量为15～20 MeV，电子束流平均功率可达1.5 kW[11]。电子经磁场偏转、准直后轰击金属钨靶，发生轫致辐射，产生高能光子，光子与钨靶核发生(γ,n)反应产生中子。由(γ,n)反应产生的中子主要为快中子(初级中子)，能谱分布的峰值在1 MeV附近[12]。出射的初级中子慢化后，可获得能谱连续的慢化中子(次级中子)。次级中子经准直后，进入中子飞行管道，用于中子核数据测量实验[13]。

图1 TMSR白光中子源布局Fig.1 Layout of TMSR photo-neutron source

TMSR-PNS的中子产生靶系统由两部分组成，即金属钨靶和中子慢化体。金属钨靶为直径5 cm、厚度4.8 cm的圆柱体。LINAC输出的电子束流直接轰击金属钨靶的底面，产生初级中子。中子慢化体材料为聚乙烯，用于慢化从金属钨靶出射的初级中子，生成次级中子束流。

根据不同需求，中子慢化体可设计成不同的结构。为提高中子束流的利用率，在TMSR-PNS实验装置运行的后续规划中拟从不同角度引出数条次级中子束流，用于不同目的的实验测量。

2 能量分辨率函数

基于白光中子源及飞行时间谱仪开展中子核数据测量实验时，所测中子束流的能量范围非常广，可达数个量级。因测量数据含实验误差，特别是对于可分辨共振区，由于实验测量的共振截面数据中包含中子能量分辨率、多普勒效应等多种因素造成的共振峰展宽，无法直接与理论计算的数据进行比较。因此，需用实验数据对应的能量分辨率对理论数据进行展宽，才能用于两者之间的比较。而在实验所测的宽中子能量范围内，能量分辨率(energy resolution, ER)并不是单一的确定值，ER将随中子能量而变化。在此将ER随中子能量发生变化的函数称为能量分辨率函数(energy resolution function, ERF)。基于飞行时间谱仪测量中子能量时，在非相对论能区，中子能量E与中子飞行时间t之间的关系由E=m(L/t)2/2确定，其中，L为中子的飞行距离。因此，ERF与所测中子的飞行时间分布函数ФE(t)对应。ФE(t)主要受到以下几个因素的影响。

1) 飞行时间测量中起始时间的不确定度，其时间分布函数用I1(t1)表示。在电子加速器运行中，电子束流是脉冲式束团结构，束团具有一定的时间结构和时间宽度。每个束团包含大量的电子，实际测量不可能记录每个电子准确的打靶时间。因此，对于1个电子束团打靶产生的多个中子，飞行时间的起始时刻使用电子束流的束团起始时刻。从而导致飞行时间的起始时刻不确定度与电子束流的束团时间结构密切相关。电子的束团时间结构和宽度由LINAC的设计运行参数决定，一般为高斯型或矩形时间结构，如图2所示。

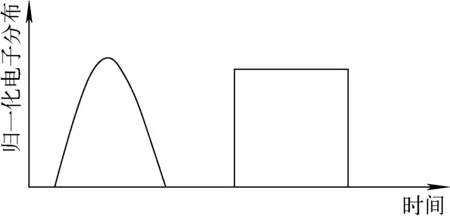
图2 两种电子束流束团时间结构示意图Fig.2 Time structure of two kinds of electron bunch

2) 中子的实际产生时间及慢化时间的不确定度，其时间分布函数用I2(t2)表示。中子并不是在电子入射至金属钨靶的瞬时时刻产生的，而是两步反应过程：(e-,γ)和(γ,n)反应。γ光子在金属钨靶中的射程相对较长，因此中子在靶中的产生位置是不确定的。另外，中子在出射过程中与钨靶核、慢化体中的原子核发生碰撞而改变速率和方向(中子慢化过程)。因此，中子在靶、慢化体中一般不沿直线路径运动，如图3所示。由此导致测量的飞行时间与中子的实际飞行时间存在偏差。这种偏差的时间分布形状与电子束流能量、中子产生靶及慢化体的几何结构等密切相关，只能通过Monte-Carlo模拟的方法获得。

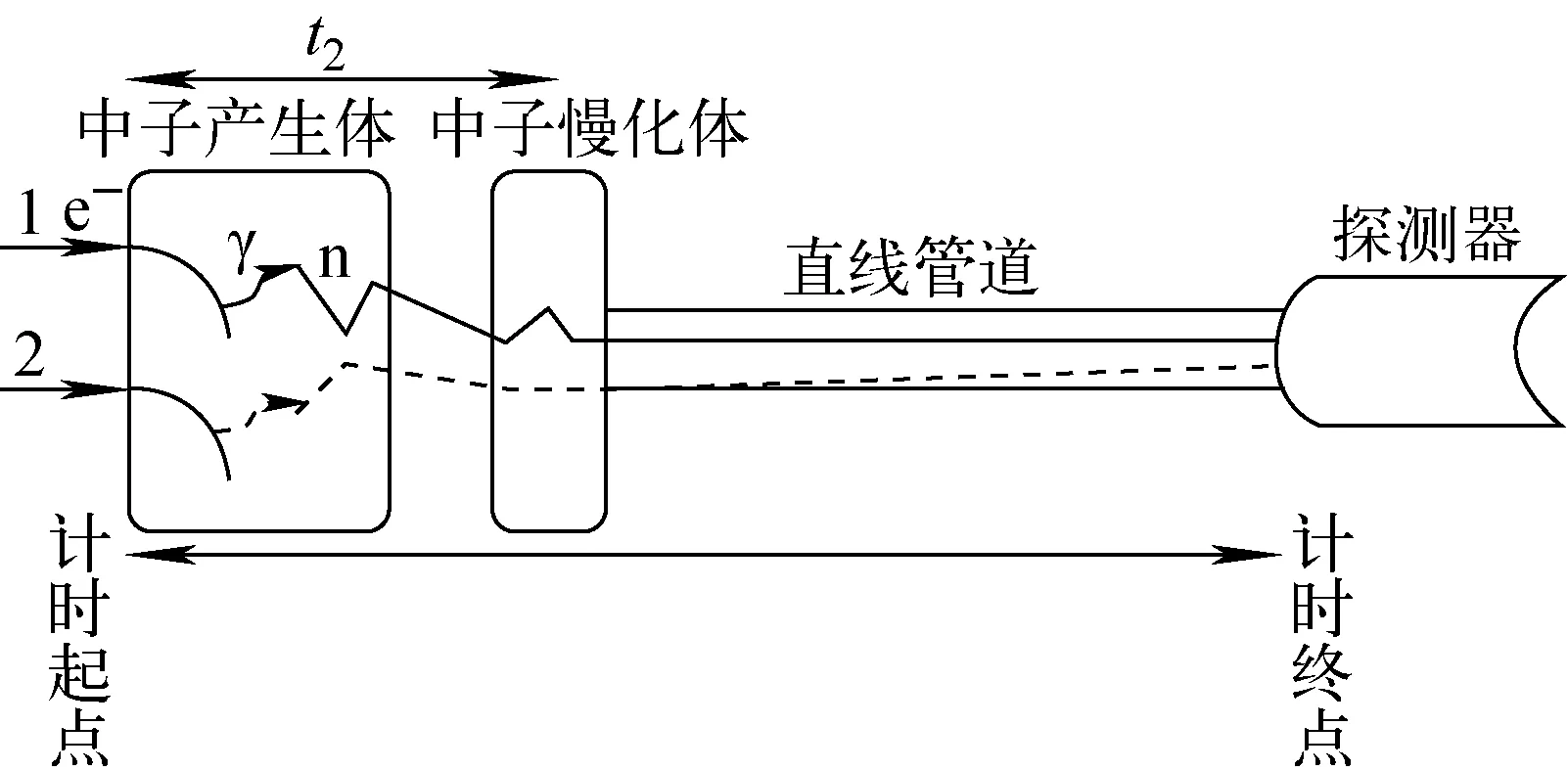
图3 中子的产生及慢化过程对飞行时间测量的影响示意图Fig.3 Influence of neutron generation and moderation process on measurement of time of flight

3) 中子探测器系统的时间测量的不确定度，其时间分布函数用I3(t3)表示。实际测量中，中子探测器具有一定的体积，中子在探测器中被吸收的具体位置是不确定的。另外，实验测量所用的电子学、数据获取等系统的时间特性也会影响飞行时间测量。目前核数据测量实验中所使用的设备都具有很好的时间响应特性，一般可以用高斯型、矩形或e指数型分布函数来表征。

实验测量中所测中子飞行时间的总时间分布ФE(t)，是以上3个方面的因素综合作用的结果。ФE(t)的表达式如下：

ФE(t)=I1(t1)⊗I2(t2)⊗I3(t3)

(1)

式中：⊗表示卷积；t1、t2、t3分别表示该时间分布函数所对应的一组参数；I1(t1)由电子加速器的运行参数确定，与出射中子能量无关；I3(t3)由探测器、电子学的时间特征参数确定，时间分布形状简单，一般也可认为与所测中子能量无关；I2(t2)与出射中子能量相关，时间分布形状较复杂，且只能通过Monte-Carlo模拟方法获得。因此，本文重点分析该部分时间分布函数的特性。

由于不同的中子源装置具有不同的设计和实验条件，在确定ERF函数的形式及其参数时，需根据装置的实际结构进行分析计算。目前，国际上使用较为广泛的一类分辨率函数形式为RPI分辨率函数[14]。世界上主要的白光中子源飞行时间谱仪在描述中子ERF时均采用了RPI函数，如n_TOF、GELINA等。RPI函数包含了前文所述的影响中子ER的3种因素——I1(t1)、I2(t2)、I3(t3)。其中，I2(t2)时间分布用1个6自由度的卡方函数与两个指数函数之和的形式来描述：

(2)

式中：参数A0为归一化常数；A2、A4为自由参数；参数τ、Λ、A1、A3、A5随中子能量的变化而变化。式(2)右侧大括号中的第1项为卡方分布，第2项为e指数分布。其中，e指数分布项主要用于描述I2(t2)时间分布中的“长尾部分”，该项与靶结构及几何尺寸密切相关。当靶结构、慢化体结构简单且体积较小时，I2(t2)时间分布中不含e指数衰减成分，式(2)中右侧大括号中的第2项可省略[2]，即：

(3)

结合TMSR-PNS的中子产生靶及慢化体结构简单且体积尺寸较小的实际情况，本工作采用式(3)所示形式来研究TMSR-PNS的ER函数。式(3)中：参数τ和Λ与所测中子能量E相关。τ、Λ的函数关系可用式(4)、(5)所示形式来描述[14]：

Λ(E)=Λ0+Λ1lnE+Λ2(lnE)2+Λ3EΛ4

(4)

τ(E)=τ1e-τ2E+τ3e-τ4E+τ5+τ6Eτ7

(5)

两个参数τ、Λ既与中子能量E相关，同时又与时间分布IE(t)耦合，因此IE(t)可用来描述不同能量中子的时间分布。

3 时间分布的Monte-Carlo模拟

式(3)所示的时间分布与电子打靶后的中子产生过程及中子从靶体、慢化体中溢出的过程相关，需通过Monte-Carlo模拟获得。本工作采用Geant4程序进行相关模拟，选用版本为10.04.p02[15]。

3.1 几何模型及模拟方法

TMSR-PNS的中子产生靶由金属钨靶和中子慢化体两部分构成。金属钨靶材料为天然钨，中子慢化体材料为聚乙烯[16]。构建了图4所示的Geant4模拟模型，即钨靶为直径5 cm、厚度4.8 cm的圆柱体，中子慢化体为球壳状聚乙烯，内径为25.3 cm，厚度为10 cm。其中，r=2.5 cm为钨靶半径，L=4.8 cm为钨靶厚度。钨靶柱体侧表面距离聚乙烯慢化体内表面的距离R-r=22.8 cm，聚乙烯球壳的厚度为D=10 cm。电子束流从钨靶的一个底面中心射入靶体。

为计算从慢化体表面出射中子的时间分布，开展从电子轰击钨靶到中子从慢化体表面溢出的全过程模拟。模拟中，中子飞行的起始时间为电子轰击钨靶的时刻ts=0，终止时刻为中子从慢化体表面溢出的时刻te=t，时间差Δt=te-ts即为模拟中所获得的中子飞行时间。电子束流从钨靶底面中心垂直xy平面向里(图4)射入钨靶，束流的能量分布为均值15.5 MeV、方差0.3 MeV的高斯分布。电子束轰击钨靶的束斑服从均值为零、方差为1 mm的二维高斯分布。模拟中近似认为从慢化体表面溢出并进入飞行管道的中子沿直线飞行，当中子飞行管道的入口直径与中子产生靶纵截面几何尺寸相当时，这种近似不会导致中子束流的时间分布形式发生变化。

图4 Geant4模拟中所用的中子靶系统模型Fig.4 Geometry of target system used in Geant4 simulation

模拟中从电子入射钨靶开始，追踪、记录之后发生的每步物理过程。包括电子与钨靶的轫致辐射反应、光子的(γ,n)反应以及初级中子与靶核的碰撞和在慢化体中的慢化过程。通过统计不同能量的出射中子计数随飞行时间的变化，获得出射中子的时间分布。考虑到初级中子产生的主要机制为光子与钨靶核发生(γ,n)反应，为提高模拟计算效率，当跟踪到γ光子溢出钨靶体时，可认为γ光子不会产生中子，从而停止跟踪该γ光子的后续物理过程。通过模拟给出慢化体表面溢出的能量为E的中子数在时间维度Δt上的分布。

3.2 时间分布的模拟结果

图5示出了从慢化体外表面向外出射的中子的能量-时间分布二维图。图5中，纵轴为中子的能量，横轴为电子轰击钨靶时刻至中子溢出时刻的时间差Δt。从图5可看出，中子从产生到出射所需时间的跨度较大，在10 ns到10 ms之间均有分布。中子能量在低于0.1 eV的热能区以及大于105eV的高能区分布较密集。其中高能区主要是未与慢化体核碰撞而直接出射的中子，热能区主要是初级中子被慢化体慢化后出射的中子。

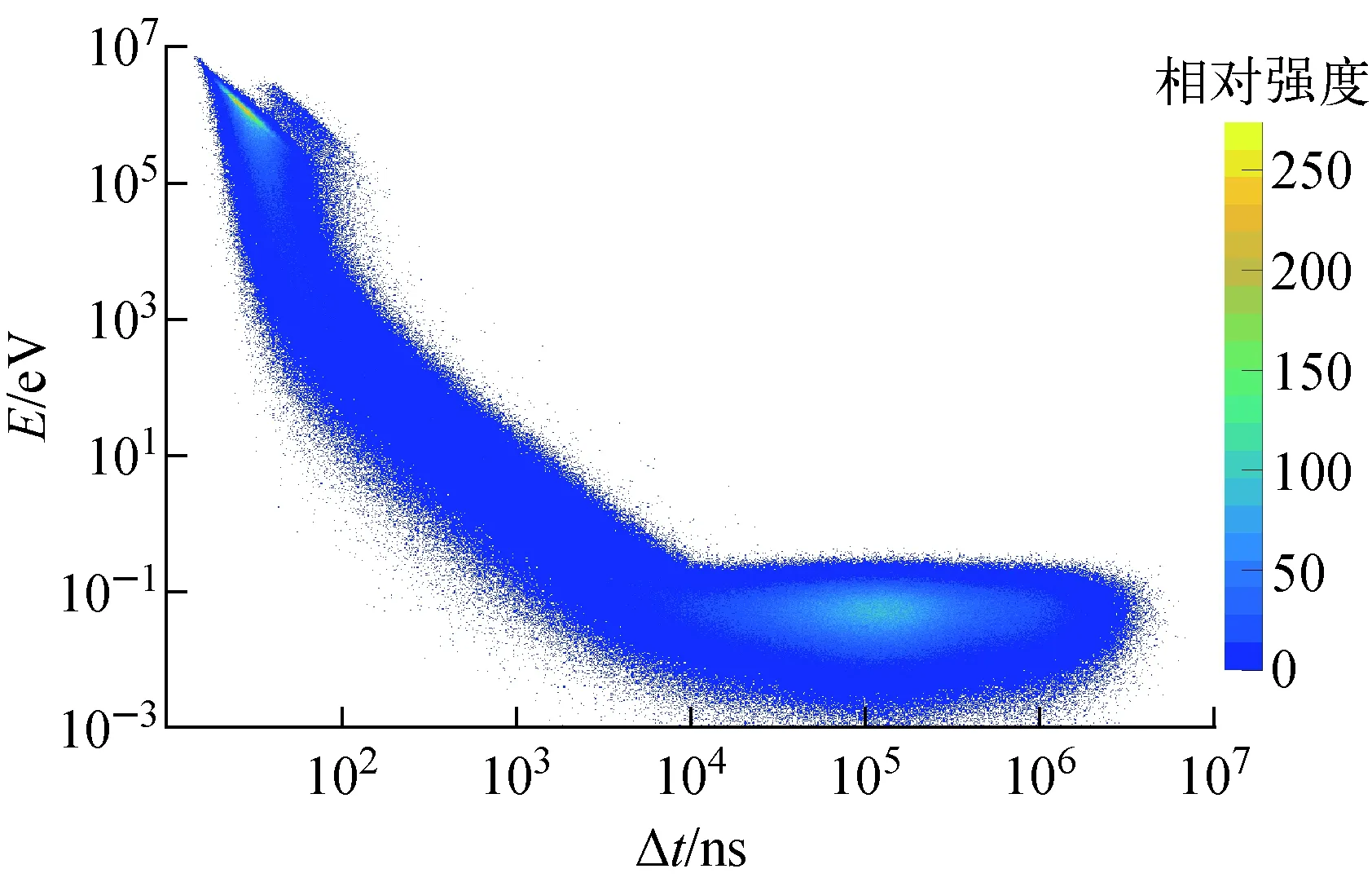
图5 不同能量中子的时间分布二维图Fig.5 Two-dimensional matrix of time distribution of neutrons with different energy

从图5可看出，当在纵轴选定一个中子能量E及一个合适的小能量区间ΔE后，将E±ΔE/2范围内的中子向横轴投影，即可获得能量为E的中子飞行时间分布。作为示例，图6示出了部分能群中子的时间分布。应指出，当能群划分规则与图6所示不相同时，投影得到的时间分布曲线会发生变化，但分布曲线的形状均可由式(3)描述。

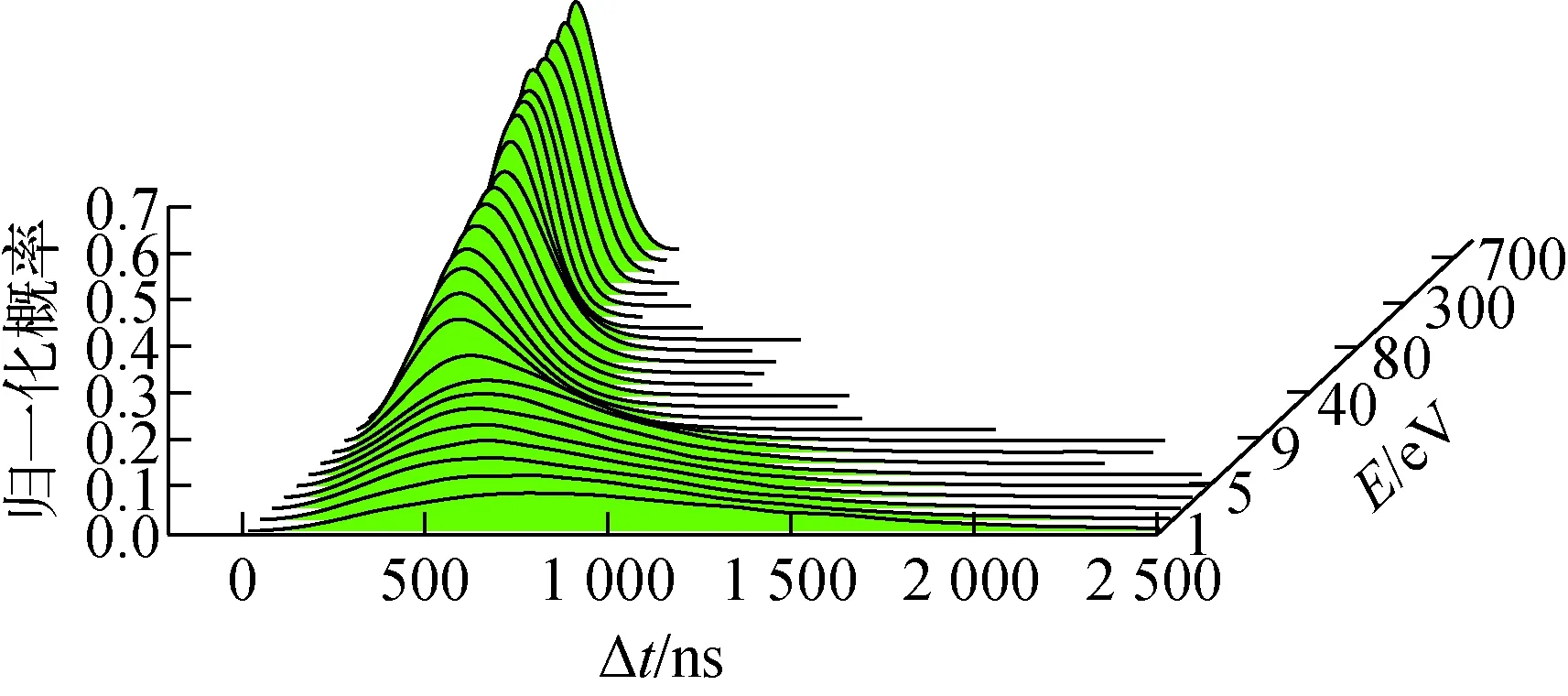
图6 不同能群的中子飞行时间分布Fig.6 Neutron TOF distribution of different energy groups

4 时间分布分析

由图6可看出，随着出射中子能量的变化，时间分布的宽度、高度均发生显著变化。对于某一确定的中子能量E，时间分布IE(t)可用式(3)拟合。为描述时间分布IE(t)随中子能量E的变化，需根据式(4)、(5)确定参数τ、Λ随中子能量的变化关系。当函数τ(E)、Λ(E)确定后，对于任意给定的能量E，可根据式(3)直接计算相应的时间分布。

4.1 时间分布拟合

采用数据分析软件ROOT的TMinuit工具包[17]，并基于式(3)对图6所示时间分布进行拟合。拟合中选择的中子能量范围为1 eV～100 keV，覆盖了TMSR-PNS飞行时间谱仪开展实验测量的可分辨共振能区。将所选能量范围中每个量级平均分为9个能群，拟合得到各个能群对应的τ和Λ。表1列出了部分能群的拟合参数及结果。

作为示例，图7示出了中子能量为15 eV和1.5 keV的拟合结果。

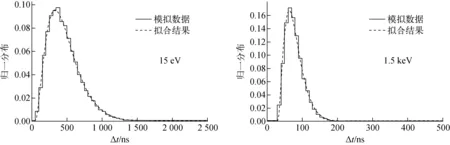
图7 中子飞行时间分布及使用式(3)的拟合结果示例Fig.7 Examples of neutron distribution of TOF and fitting result

4.2 τ、Λ参数分析

参数τ、Λ为中子能量E的函数。图8示出了表1所列的τ、Λ(圆点)随中子能量E的变化关系。同样利用TMinuit工具包，依据式(4)、(5)，对Λ、τ随中子能量E的变化关系进行拟合。图8中实曲线为拟合结果，所得拟合参数列于表2。图8中所示τ的“离散”主要与表1所列能群的划分方式相关。本文所采用的分群方式(1 eV～100 keV，每个量级平均分为9个能群)使参数τ有较大的离散，而参数Λ的离散较小。不同的能群划分规则，τ的离散程度会略有差别，但其平均变化趋势，即基于式(5)的拟合结果并不发生大的改变。

表1 部分能群的时间分布拟合结果Table 1 Fitting results of time distribution for different energy groups

图8 τ、Λ随中子能量E的变化关系拟合Fig.8 Fitting procedure of parameters τ and Λ vs. neutron energy

需指出，表2中所列部分参数的数值为0。参照文献[2,14]中的论述，表2数值为0的参数可根据被拟合数据的实际形状分布进行灵活调整。本工作中，设置相关参数为0即可获得很好的拟合结果，这从图8可看出。

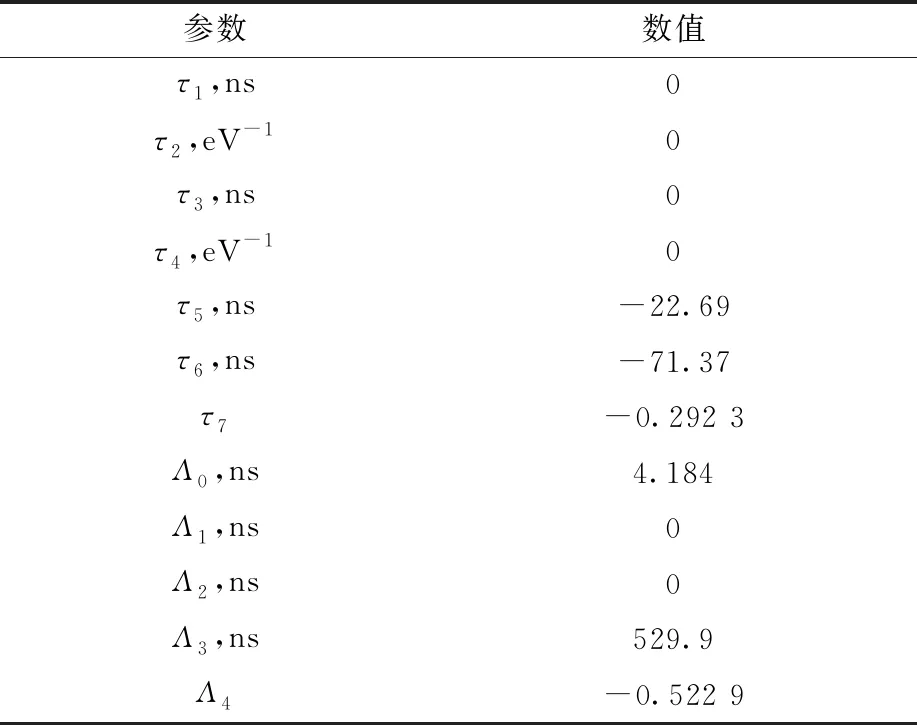
表2 τ、Λ参数拟合结果Table 2 Fitting results of parameters τ and Λ

4.3 时间分布函数检验

前文中，通过蒙特卡罗模拟及拟合不同能群(表1)的中子飞行时间分布，获得了时间分布函数。在将所获时间分布函数用于实验数据分析时，希望该函数适用于任何能群，而不依赖于数据拟合时所选的能群结构。为验证其适用性，在蒙特卡罗模拟所获得的时间分布数据(图5)中，选取4个不同于表1所列能群的新能群，对应的能量点E分别为0.75 eV、225 eV、2.25 keV、150 keV。利用表2所列参数及式(3)、(4)、(5)计算了对应的时间分布，如图9中蓝色实线所示。图9同时给出了4个能群对应的模拟数据(归一化实线直方图)。由图9可看出，时间分布函数计算的结果与模拟数据符合很好。这说明，在TMSR-PNS飞行时间谱仪的测量能量范围内，本工作所获得的时间分布函数，可在连续的能区范围内用于计算不同中子能量对应的时间分布，从而确定相应的ER函数。

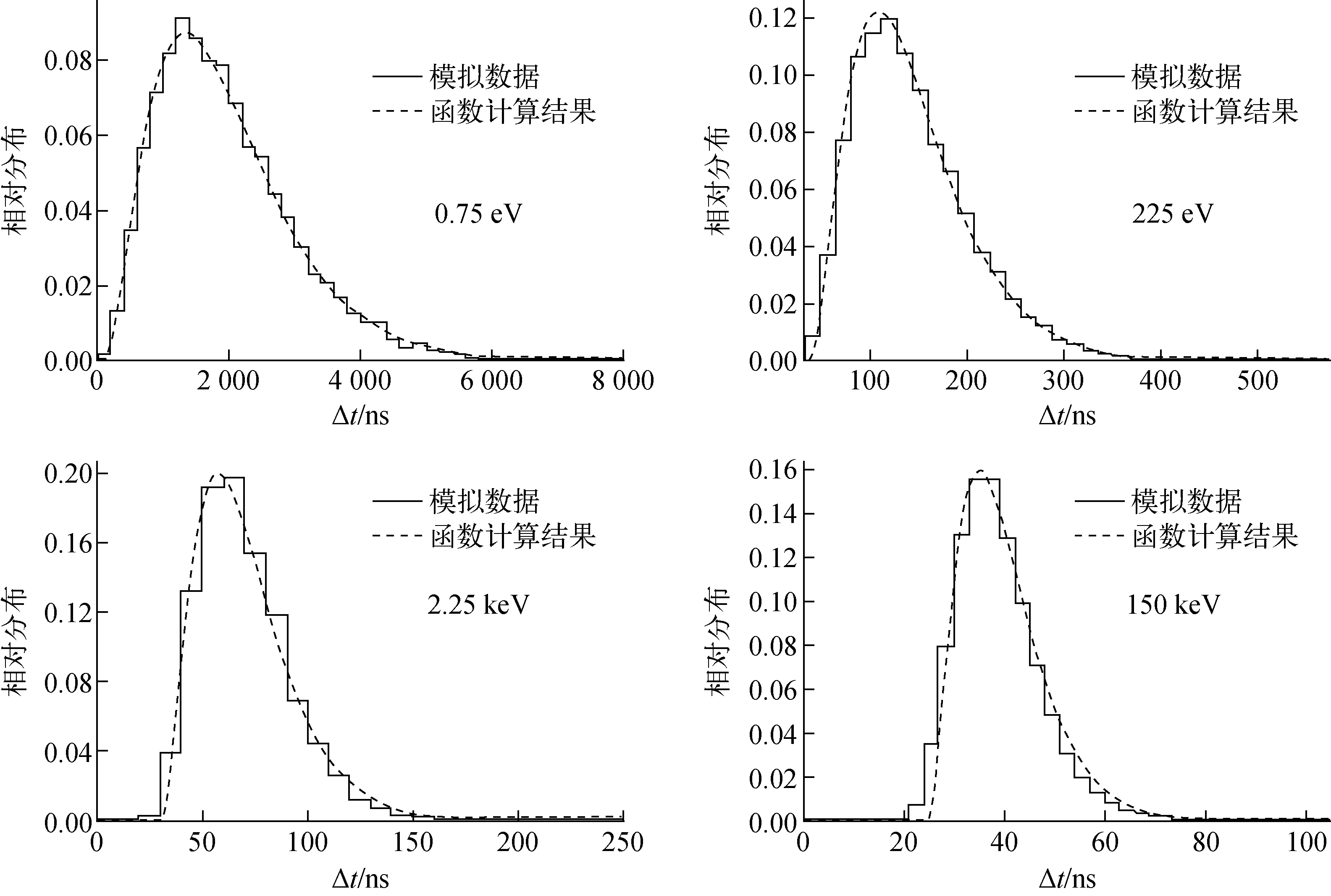
图9 计算的时间分布与Geant4模拟数据的比较Fig.9 Comparison of time distribution between calculation and Geant4 simulation

5 总结

本工作利用Geant4蒙特卡罗工具包，构建了TMSR-PNS的中子产生靶系统，模拟了电子束流打靶后出射的中子束流的时间分布。通过对模拟的中子数据进行能群划分，利用RPI函数形式分析了中子束流的时间分布与中子能量之间的关系。获得了在TMSR-PNS飞行时间谱仪测量能量范围内，用于计算不同中子能量对应时间分布的解析函数。该解析函数可用于对理论计算的理想共振截面数据进行展宽，使实验数据与理论数据之间可进行比较，从而确定所测数据的共振峰参数。