基于MOOSE平台的棒状燃料元件性能瞬态分析程序开发与验证
邓超群,向烽瑞,贺亚男,牛钰航,巫英伟,田文喜,秋穗正,苏光辉
(西安交通大学 动力工程多相流国家重点实验室,陕西 西安 710049)
福岛核电站事故后,提出了众多事故容错燃料(ATF)包壳和芯块选型[1],旨在提高燃料抵抗事故的能力。国内外学者针对瞬态事故下ATF行为开展了广泛研究。部分研究对FRAPTRAN、TRANSURANUS等传统燃料性能分析程序进行改造,分析了U3Si2[2]、FeCrAl[3-4]和SiC[5]等在瞬态事故工况下的性能,但难以实现如陶瓷基包覆颗粒弥散燃料(FCM)[6]、涂层包壳[7]等复杂结构燃料的精细建模。因此需开发新的瞬态燃料性能分析程序,准确评估瞬态事故条件下ATF的性能。
目前,基于商用有限元平台如COMSOL[6]、ABAQUS[8]、ADINA[9]等开发的复杂结构ATF性能分析程序均缺乏瞬态事故分析功能。美国爱达荷国家实验室(INL)基于更具扩展性的开源多物理场有限元平台MOOSE[10]开发的BISON程序[11]能够模拟瞬态事故下ATF燃料行为,但国内无法获得其使用权。
西安交通大学核反应堆热工水力研究室(NuTHeL)基于MOOSE平台开发了棒状燃料元件稳态性能分析程序BEEs[12],该程序包含了燃耗、冷却剂焓升、芯块密实化、重定位、热膨胀、晶粒长大、裂变气体释放、裂变产物肿胀、间隙换热、燃料内压演化等行为模型及非线性燃料元件热膨胀系数、导热系数等物性模型。
为实现反应性引入事故(RIA)和冷却剂丧失事故(LOCA)瞬态事故工况下的燃料性能精确模拟,本文针对UO2-Zr燃料棒,基于棒状燃料元件稳态性能分析程序BEEs进行瞬态功能扩展,并开展程序模块验证与整体功能验证。
1 数学物理模型
BEEs程序基于MOOSE平台的张量力学模块、接触模块和热传导模块进行开发,底层的网格离散和求解计算依赖于PETSc、Hypre、MPICH和LibMesh等功能库,其整体框架示于图1。为实现RIA和LOCA瞬态事故下燃料性能分析,在BEEs程序中添加了包壳弹塑性、高温蠕变、高温相变、高温氧化和包壳失效等模型。
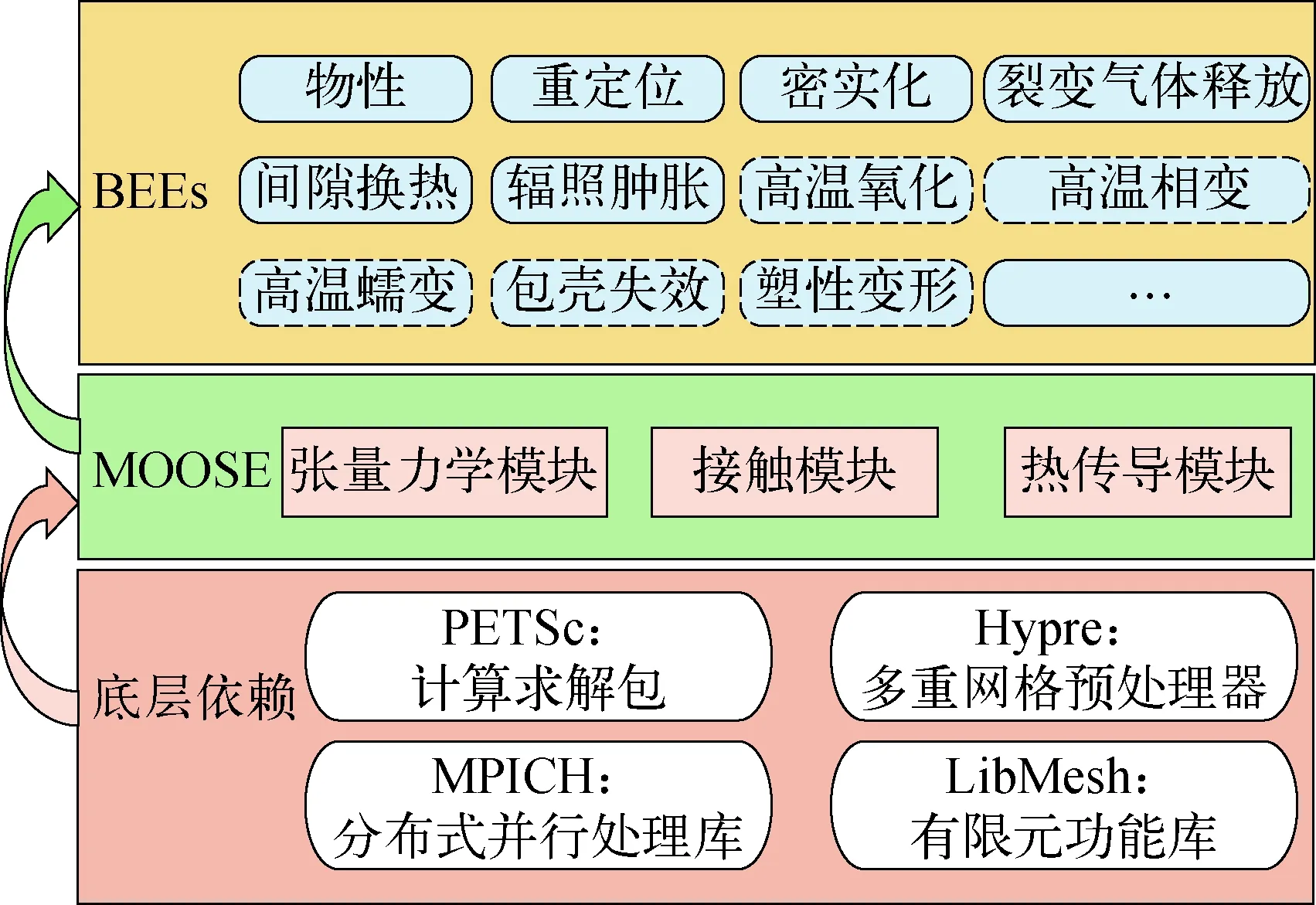
图1 BEEs程序结构框架Fig.1 Diagram of BEEs code framework
1.1 弹塑性模型[13]
在发生屈服前,用Hooke定律描述包壳变形:
σ=ε·E
(1)
其中:σ为应力,MPa;E为弹性模量,MPa;ε为应变。
当包壳的应力达到屈服极限后,用幂次定律描述包壳的塑性变形:
(2)
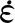
1.2 高温蠕变模型
发生LOCA时,包壳在燃料棒升温和内压作用下发生高温蠕变,导致局部产生较大变形。BEEs程序中针对包壳的高温蠕变速率计算以Norton方程[14]的形式给出:
(3)
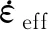

表1 Zr4包壳蠕变常数Table 1 Creep constant of Zr4 cladding
1.3 高温相变模型
随着包壳温度上升,锆合金晶体从六角α相结构转变为立方形β相结构。锆包壳的相变速率可用下式[15]表示:
(4)
其中:y为β相锆的体积分数,%,0≤y≤1;t为时间,s;k为速率常数,s-1;ys为平衡态β相锆的体积分数,%。模型适用于包壳升温速率小于100 K·s-1。
(5)
(6)
其中:w为局部氢浓度,ppm;k0为动力常数,s-1;E为等效激活能,J;kb为玻尔兹曼常数,J·K-1;km为常数,s-1。对于Zr4包壳,k0=60 457+18 129|Z|(Z为加热(或降温)速率,K·s-1,0.1≤|Z|≤100 K·s-1);E/kb=16 650 K。
常数km取值为:
(7)
相变转换起始温度为:
(8)
(9)
1.4 高温氧化模型
LOCA下燃料元件温度快速上升,包壳氧化速率远大于正常稳态工况,其氧化动力学方程以抛物线形式给出[16]:
(10)
(11)
其中:δ为氧化物厚度,m;w为氧化物质量,kg;Aδ和Aw为氧化系数,m2·s-1;Qδ和Qw为激活能,J·mol-1;R为通用气体常数,J·mol-1·K-1;Ti为金属-氧化层界面温度,K,Ti=To+q″δ/λ,To为冷却剂温度,K,q″为包壳外表面热通量,W·m-2,λ为氧化锆的导热系数,W·m-1·K-1。
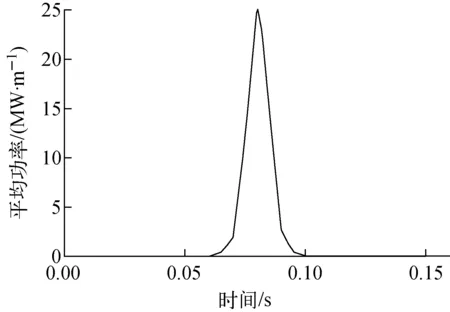
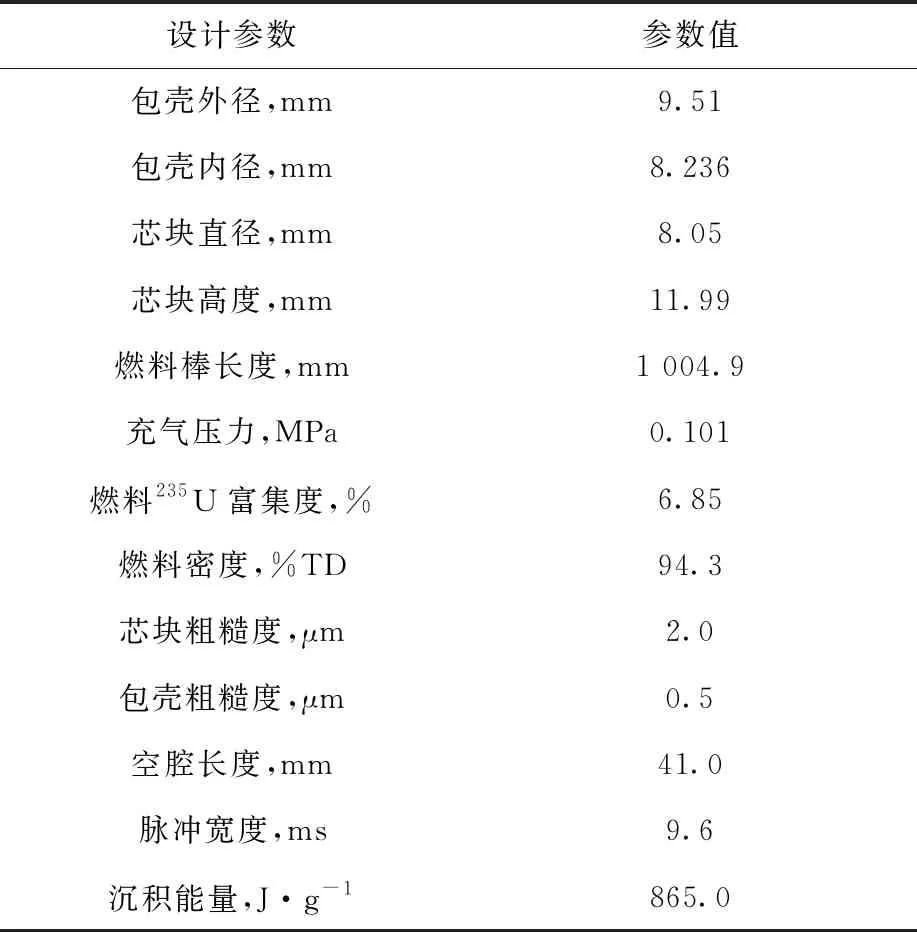
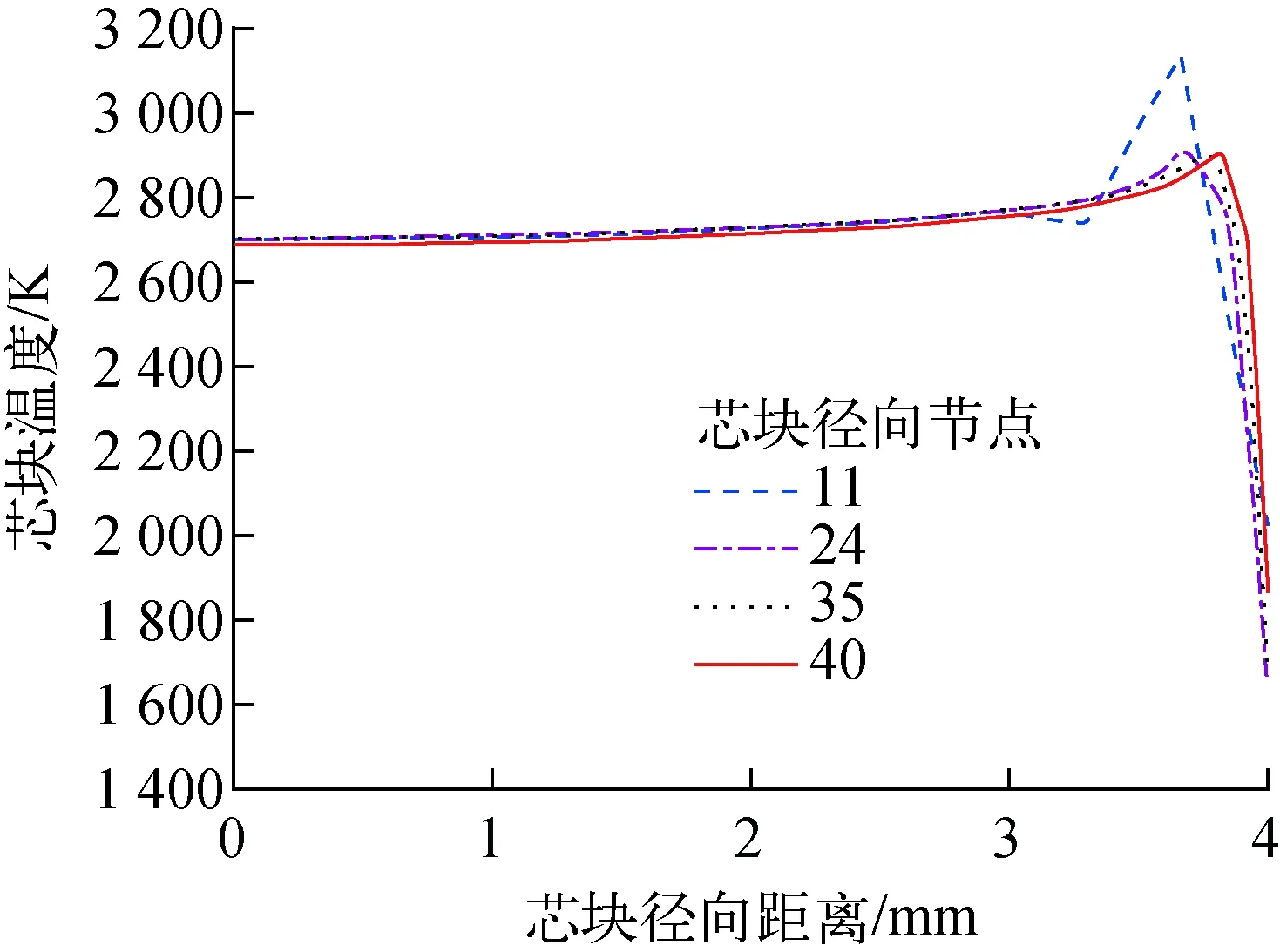
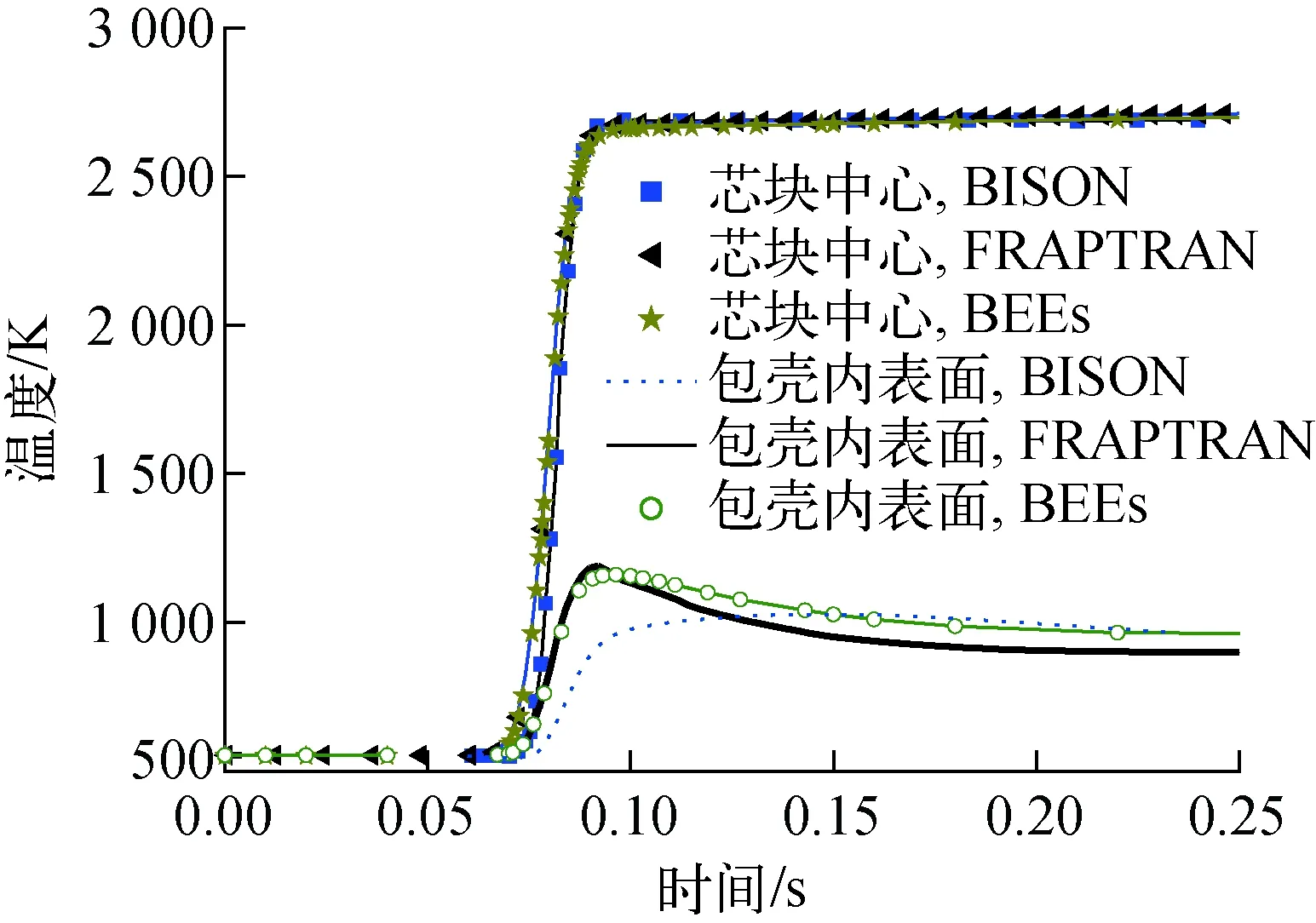
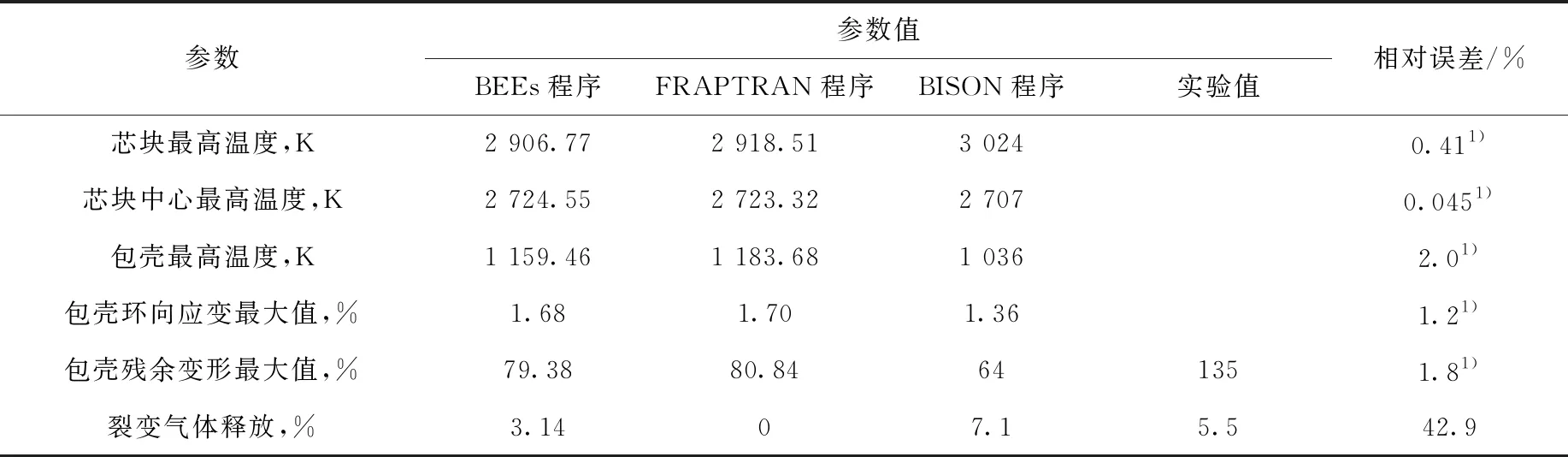
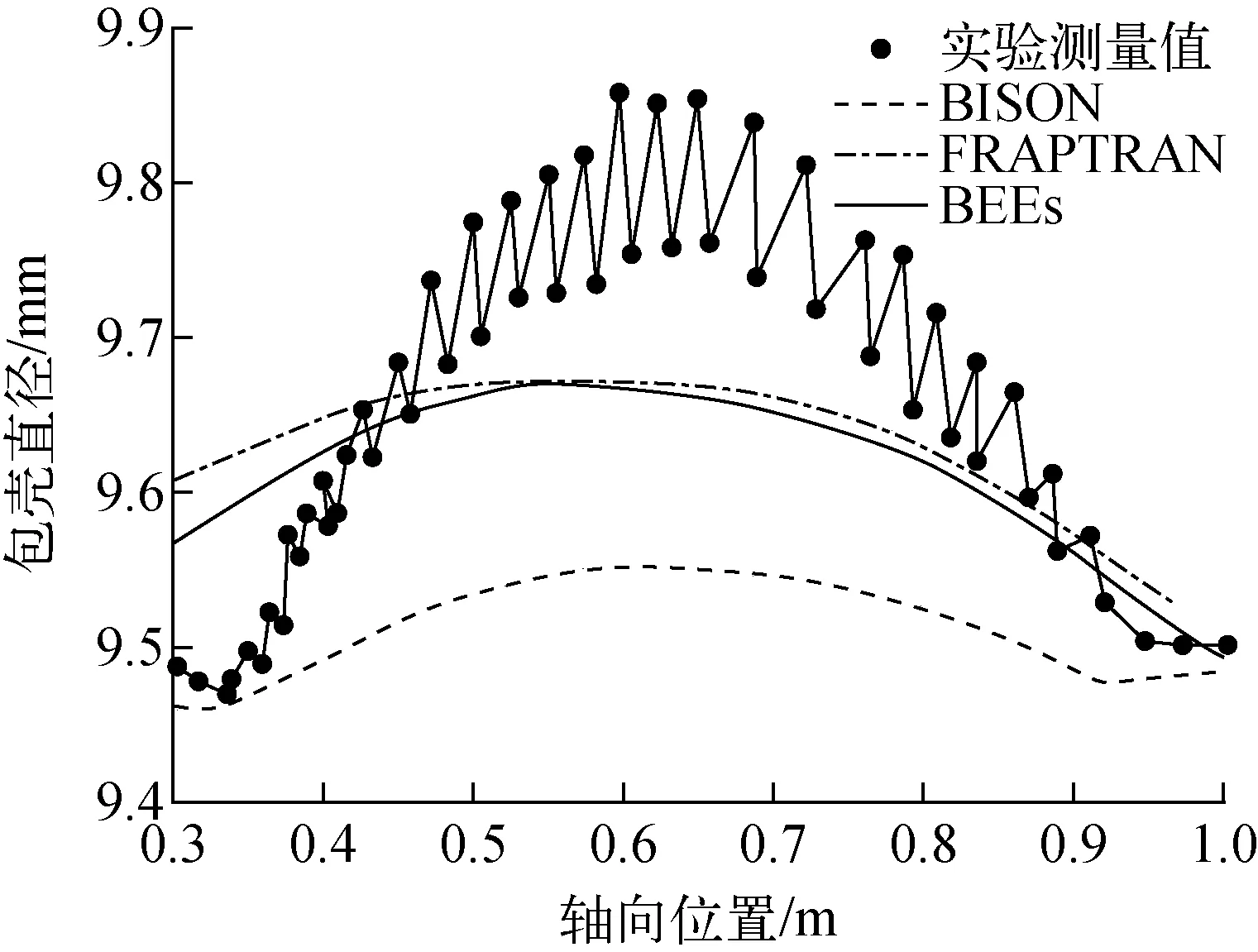
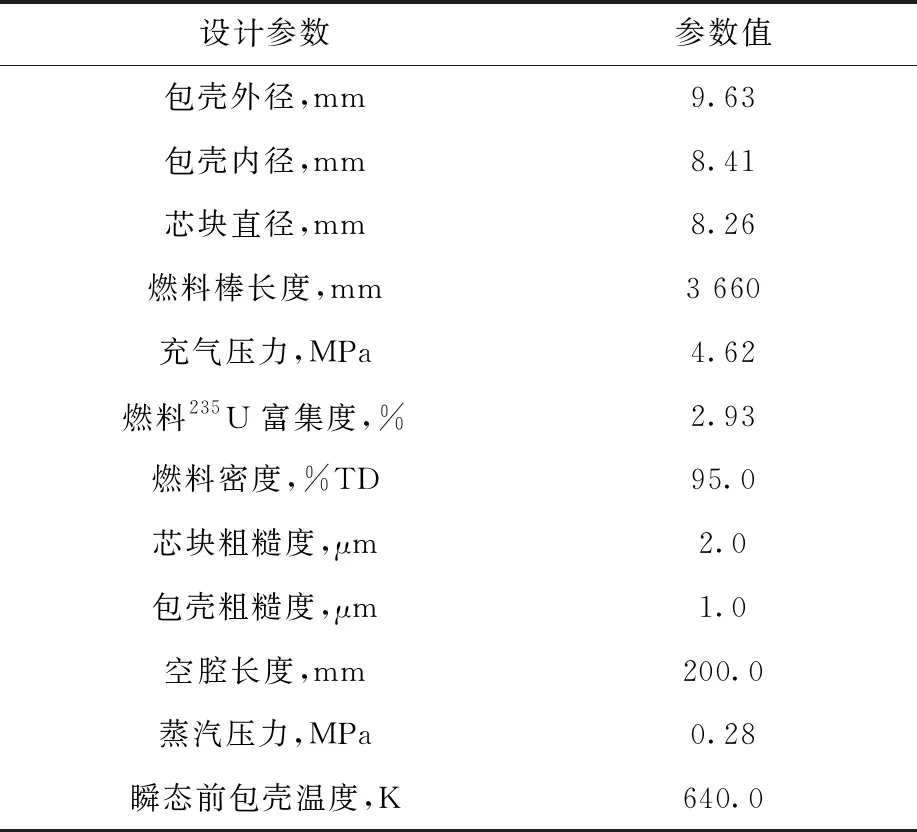
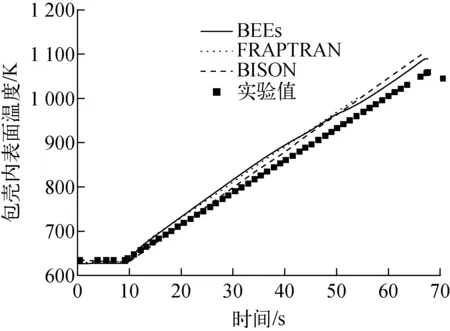
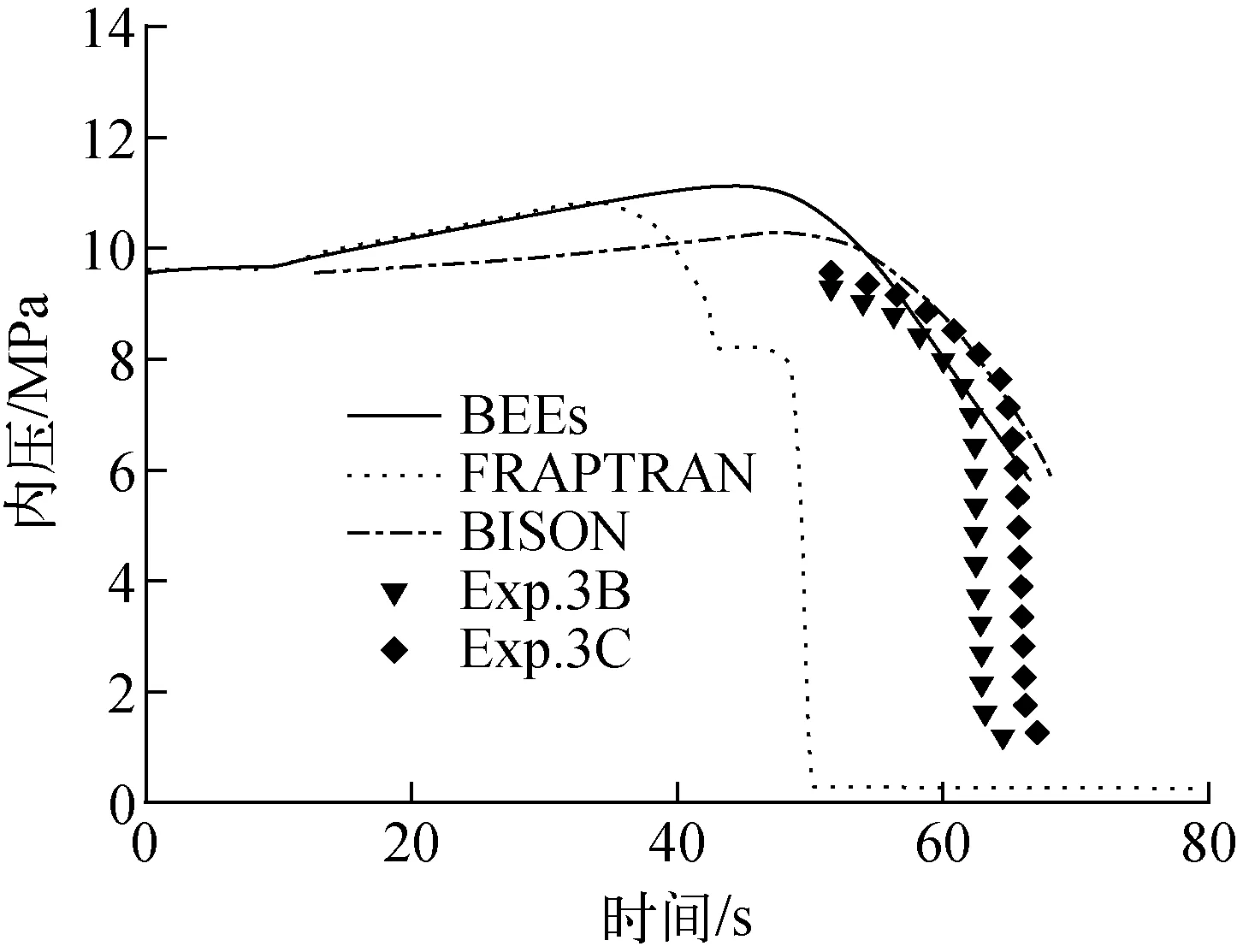
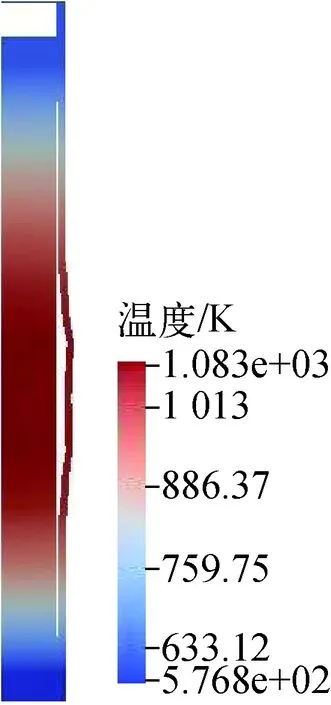
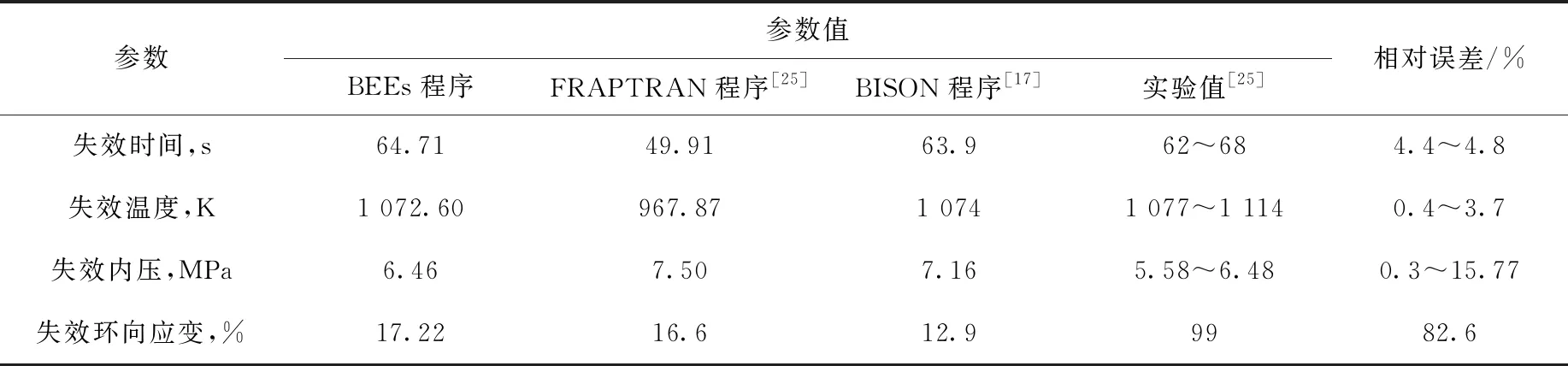
高温氧化模型适用于Ti>673 K。模型常数取值列于表2。当673 K 表2 氧化关系式参数Table 2 Parameter of oxidation relationship 包壳在RIA中由于芯块和包壳产生的强烈相互作用(PCMI)产生的较大应力导致失效,在LOCA中由于发生塑性变形使其鼓胀破裂。BEEs程序中采用包壳局部应力限制准则和塑性“失稳”准则来判定包壳失效。事故过程中,包壳状态满足其一即判定包壳失效。 1) 包壳局部应力限制准则 (12) 其中:σθ为包壳环向应力,MPa;σb为包壳破裂临界应力,MPa;a和b为模型常数,根据表3中参数插值获得;Δη为包壳氧化物质量分数增量,%;rcl,o和rcl,i分别为包壳外径和内径,m;w为局部氢浓度,ppm;ρZr为包壳密度,kg·m-3;rmet,o为未氧化包壳厚度,m。 表3 局部应力限制准则参数Table 3 Parameter of local stress limiting criterion 2) 塑性“失稳”准则 (13) 为确保程序中模型添加的正确性,本文首先对BEEs程序添加的弹塑性计算、高温蠕变、高温相变和高温氧化模块进行单一模块验证。 弹塑性模块验证中,将边长为1 m的Zr样品保持恒温,下方固定,上方施加恒定速率的位移,计算参数列于表4,获得拉伸过程中的总应变与应力关系,并与实验数据[13]进行比较,如图2所示。在达到屈服极限后样品硬化,应力应变曲线斜率发生变化,达到抗拉极限后样品断裂,程序计算终止。由图2可知,BEEs程序预测值与文献计算值和实验结果符合较好,由于理论模型未对Zr合金屈服后的均匀塑性变形和强化阶段进行区分,因此计算结果和实验曲线的趋势有所不同,在均匀塑性变形和强化阶段相比于实验值的最大相对误差分别为4.7%和11.3%。 表4 应力应变关系式验证算例参数Table 4 Parameter of validation case of stress-strain correlation Hardy tube实验[17]是为评估Zr4包壳在假定LOCA实验下的鼓胀行为而进行的瞬态实验。实验测量了升温速率为25 K·s-1时不同内压下包壳的变形情况。图3示出1.4 MPa内压条件下环向应变的对比,计算参数列于表5,包壳轴向和径向分别划分20和4个节点。当包壳处于安全限值内(环向应变低于2.78%)时,BEEs程序在环向应变低于1%范围内计算相对误差较大,最大相对误差为26.5%,当环向应变高于1%时最大相对误差为8.6%。当超过包壳安全限值时相对误差增大,但此时已判定包壳失效,不影响燃料性能的有效评估。需要注意的是,由于BEEs程序在700~900 K之间进行了低温热蠕变[18-19]与高温蠕变的插值,而BISON程序均采用高温蠕变计算关系式,因此在该温度区间内计算结果比BISON程序略高。 图3 内压1.4 MPa时包壳环向应变对比Fig.3 Comparison of cladding strain with internal pressure at 1.4 MPa 表5 Hardy tube实验设计参数Table 5 Design parameter of Hardy tube test 实验[15]中将Zr合金样品置于膨胀仪中升温(或降温),同时进行样品膨胀(收缩)量的数据采集(精度±0.1 μm)获得热膨胀量曲线,再通过杠杆法或切线法计算β相转化比例。表6列出包壳相变验证算例参数。图4示出升温(降温)速率为10 K·s-1时,BEEs程序计算的加热时β相体积分数及平衡态β相体积分数随温度的变化,并与实验值进行对比,计算结果合理。图5对比了0.1~100 K·s-1升温速率范围内β相体积分数到达10%的温度(T10%β),BEEs程序计算值相对误差均在1.85%以内。 表6 包壳相变验证算例参数Table 6 Parameter of validation case of cladding phase transformation 图4 β相体积分数随温度的变化Fig.4 Comparison of volume fraction of β phase as a function of temperature 图5 不同升温速率下T10%β的对比Fig.5 Comparison of T10%β as a function of heating rate Yoo等[20]针对Zr的氧化动力学规律进行了实验研究。将Zr合金样品经过打磨抛光和酸溶液去锈后,置于石墨恒温炉(精度为±1 K)中,用热天平(精度为±1 μg)测量氧化物的增重情况,并将氧化物增重转换成氧化层厚度的增长,实验中气体温度工况范围为773~1 073 K。图6示出BEEs程序计算的氧化层厚度与实验值[20-21]的对比。由图6可知,高温氧化模型适用于在温度较高(大于973 K)、氧化层较厚(大于10 μm)的情况,最大相对误差为11.4%。当温度较低且氧化层厚度较小时,计算误差增大。针对低温范围内的稳态工况计算,BEEs程序采用同FRAPCON一致的LEISTIKOW模型[22]。在温度为973 K时,计算值与实验值偏离可能是由于采用氧化模型未考虑掺杂元素的影响或该组实验过程中出现氧化层脱落的情况。 图6 氧化层厚度变化对比Fig.6 Comparison of oxide thickness CABRI-RIA Na-2实验[23]是IRSN同EDF、Framatome、CEA和NRC在法国合作开展的RIA瞬态实验。本文基于该算例对BEEs程序的RIA整体分析功能进行评估。实验中燃料棒的相关参数列于表7,燃料类型为UO2,包壳类型为Zr4。实验功率脉冲历史如图7所示,RIA功率脉冲峰值出现在0.08 s,平均功率峰值约为25 000 kW·m-1。模拟时在芯块轴向划分340个节点,包壳径向划分4个节点,轴向划分350个节点,网格类型为QUAD4,如图8所示。 图7 实验功率脉冲历史Fig.7 History of experimental power pulse 图8 Na-2实验算例网格划分Fig.8 Mesh partition of case Na-2 表7 Na-2实验设计参数Table 7 Design parameter of Na-2 test Na-2实验基础辐照工况末期燃料平均燃耗约为25 MW·d/kgU,为准确模拟高燃耗下芯块显著的边缘效应,在其径向划分不同网格节点,对比功率峰值节点(PPN)处芯块温度径向分布,如图9所示。芯块径向划分35个节点时与24节点和40节点的计算最大相对误差分别为0.4%和0.1%,满足计算精度要求。 图9 不同节点划分情况下PPN处芯块温度径向分布对比Fig.9 Radial distribution of pellet temperature at PPN under different nodes partitions 图10示出PPN处芯块中心温度和包壳内表面温度的变化。其中BISON程序和FRAPTRAN程序计算结果来自文献[5]。模拟时BEEs程序采用与FRAPTRAN程序相同的冷却剂边界,因此两者温度变化趋势总体一致。由图10可见,在RIA初期,BEEs和FRAPTRAN程序的温度计算值符合良好,后期温度的差异可能与程序间包壳变形程度计算不同有关。 图10 PPN处芯块中心温度及包壳内表面温度预测对比Fig.10 Comparison of pellet centerline and cladding inner surface temperatures at PPN 在RIA过程中PCMI使包壳发生较大塑性变形,长期冷却后仍有残余变形。图11示出冷却至室温时包壳直径轴向分布情况。由于BISON程序采用MATPRO塑性模型[24],而BEEs和FRAPTRAN程序均采用保守的PNNL塑性模型,因此两者计算的包壳变形高于BISON程序。此外,由于BEEs程序考虑了芯块的弹塑性变形和蠕变行为而FRAPTRAN程序模拟时将芯块作为刚体,导致BEEs程序计算值略低于FRAPTRAN程序。 表8列出Na-2实验各程序计算值与实验值对比。由表8和图11可知,各程序计算值均总体低于实验测量值,这主要是由于缺乏冷却剂及包壳约束的相关实验数据,各程序模拟时边界条件设置有偏差。此外,各程序计算PCMI时采用的无摩擦接触模型忽略了应力的轴向分量,使包壳有效应力计算偏小,进一步导致包壳变形预测值偏低。芯块两端的碟形倒角使包壳在PCMI中产生较大的局部变形,导致实验测量值在轴向会呈现局部波动,而考虑到缺乏实验芯块倒角的详细描述和PCMI计算的复杂性,当前各程序模拟过程中并未对碟形倒角进行建模,后续可通过更精确的二维、三维建模对该现象进行分析。 表8 Na-2实验各程序计算值与实验值对比Table 8 Comparison among code calculation value and test data for Na-2 图11 包壳直径对比Fig.11 Comparison of cladding diameter NRU-LOCA MT4实验[25]是PNNL在加拿大Chalk River国家实验室的NRU反应堆中开展的LOCA瞬态实验。实验中将零功率燃料棒进行辐照、升温、再淹没,测量了包壳内表面温度,实验后拆除实验段,测量了燃料棒变形。实验中燃料棒设计参数列于表9,燃料类型为UO2,包壳类型为Zr4。本文将BEEs程序与FRAPTRAN程序[26]和BISON程序[17]计算结果进行对比。模拟时网格划分如图12所示,采用网格类型为QUAD4,在燃料径向划分11个节点,轴向划分1 680个节点,包壳径向划分4个节点,轴向划分2 500个节点。 图12 MT4实验算例网格划分Fig.12 Mesh partition of MT4 test case 表9 MT4实验设计参数Table 9 Design parameter of MT4 test 图13示出中心高度处(183 cm)包壳内表面温度的对比。前10 s实验维持稳态工况,之后发生LOCA使温度上升。值得注意的是,由于FRAPTRAN程序轴向节点划分较少,其计算值取自离轴向高度183 cm最近的节点。由图13可知,BEEs程序计算结果与实验值符合良好,与FRAPTRAN和BISON程序的结果基本一致。 图13 包壳内表面中心高度处温度的变化Fig.13 Change of temperature of cladding inner surface at axial mid-plane 燃料棒内压变化对比如图14所示。由于BEEs程序采用与FRAPTRAN程序一致的温度边界条件,使燃料棒温度计算偏高,进而导致内压计算值高于实验值。针对LOCA下包壳高温变形的模拟,BEEs和BISON程序均采用连续蠕变行为模型,因此两者计算的内压变化趋势总体一致。而FRAPTRAN程序需在基于小变形的弹塑性求解及单独的鼓胀变形模块BALON2间进行模型转换[27],导致其内压计算曲线中出现明显转折点和两个峰值。 图14 燃料棒内压的变化Fig.14 Change of rod internal pressure 图15为失效时燃料温度分布云图。由于LOCA条件下的高温蠕变效应,在失效时刻包壳中间高度处会发生显著的鼓胀现象。 包壳破裂失效时的参数对比列于表10。对于包壳失效时间、失效内压和失效温度,BEEs与BISON程序计算值及实验值符合良好。BEEs与FRAPTRAN程序的误差主要由高温下包壳变形的模拟方法不同所导致,FRAPTRAN程序预测的失效参数过于保守。由表10可知,各程序计算的破裂时刻包壳环向应变相当,但由于上述程序目前均无法模拟破裂后包壳破口的真实形态,而实验数据是对包壳破口进行实际测量所得,因此模拟结果与实验数据有较大偏差。 图中将轴向高度缩短为原长0.2倍,径向长度增大为原长15倍图15 包壳失效时燃料温度分布Fig.15 Distribution of fuel temperature when cladding burst 表10 包壳失效参数对比Table 10 Comparison of parameter when cladding burst 本文对基于MOOSE平台的棒状燃料元件性能分析程序BEEs进行瞬态功能开发,并对开发的RIA和LOCA模块开展模块验证及整体验证。结果表明,BEEs程序能实现瞬态事故条件下燃料温度、力学变形、内压演变的模拟及包壳失效的预测,计算结果合理,并得到以下结论。 1) 针对瞬态功能扩展模型的验证表明:BEEs程序中添加的塑性求解模块在均匀塑性变形和强化阶段相比于实验值的最大相对误差分别为4.7%和11.3%;高温蠕变模型适用于环向应变大于1%的情况,最大相对误差为8.6%;在0.1~100 K·s-1升温速率范围内,包壳相变模型计算值的相对误差均在1.85%以内;高温氧化模型适用于温度较高(大于973 K)、氧化层较厚(大于10 μm)的情况,最大相对误差为11.4%。 2) 针对CABRI-RIA Na-2实验,BEEs程序计算值与其他程序符合良好,与FRAPTRAN程序相比,芯块和包壳温度计算最大相对误差分别为0.4%和2.0%,包壳环向应变和残余变形相对误差分别为1.2%和1.8%。由于缺乏冷却剂及包壳约束的相关实验数据和无摩擦接触模型的局限性,导致模拟PCMI时程序计算的残余变形与实验值有较大偏差。 3) 针对NRU-LOCA MT4实验,BEEs程序计算值模拟结果具有合理性,与BISON和FRAPTRAN程序对比情况良好,BEEs程序预测的包壳失效时间和内压均在实验值范围内,失效温度计算值相对误差在0.4%~3.7%之间。由于程序目前无法模拟到达破裂限值时包壳实际的破口形态,因此针对破口处环向应变的计算偏差较大。
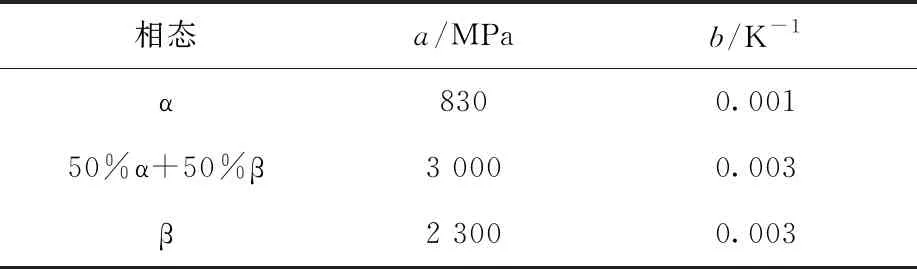
1.5 包壳失效准则[14]
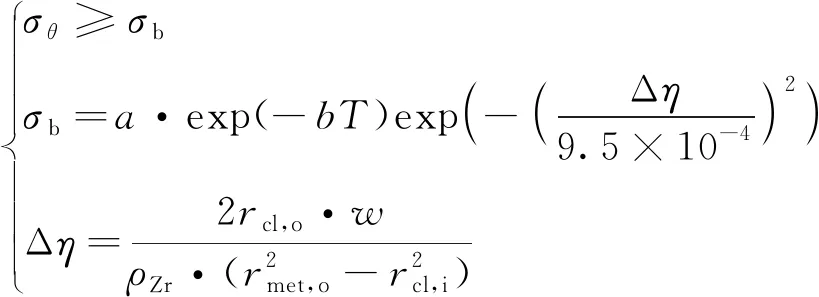
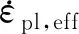
2 瞬态模型验证
2.1 包壳弹塑性求解验证
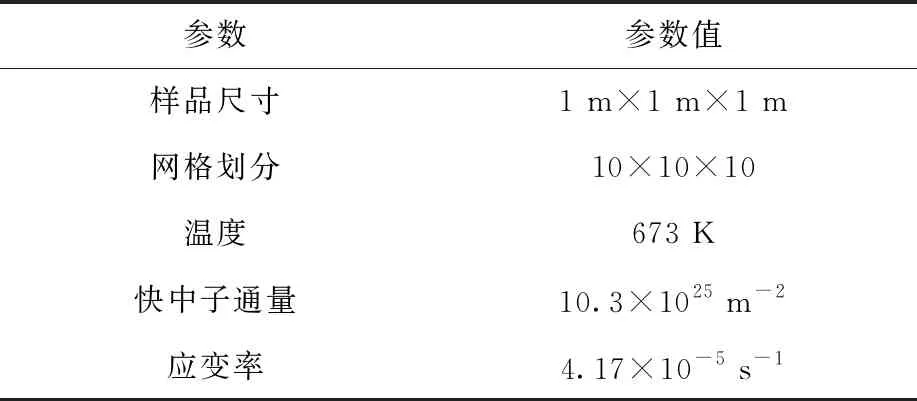
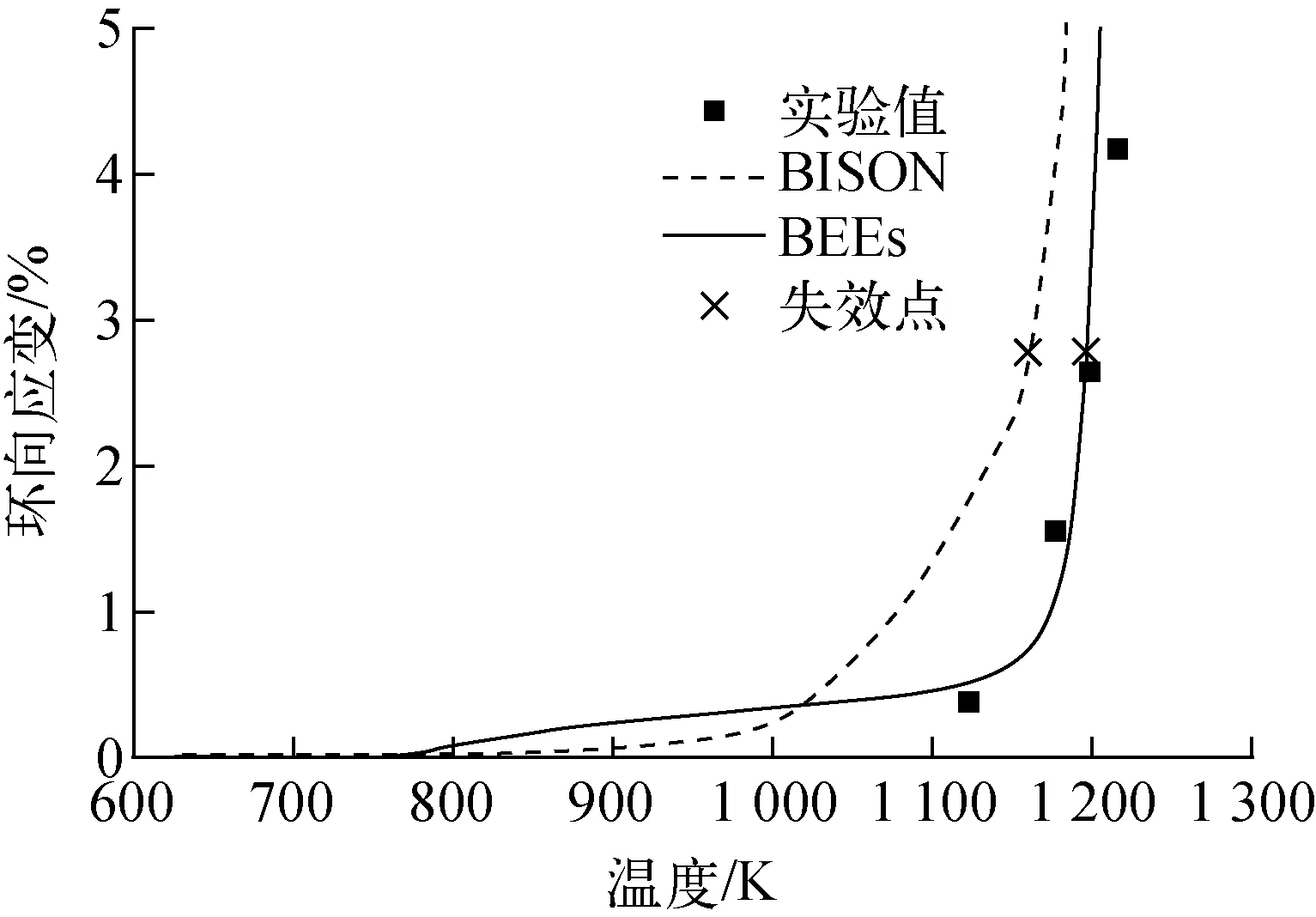
2.2 高温蠕变模型验证
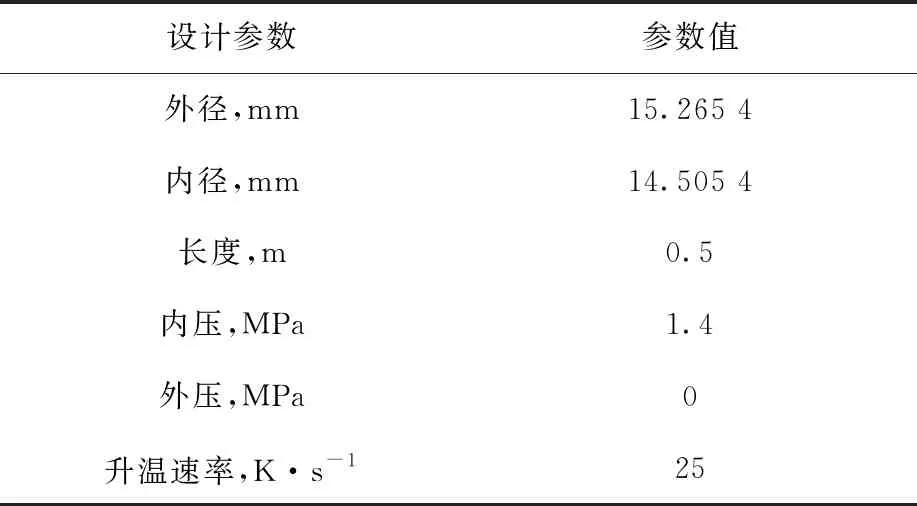
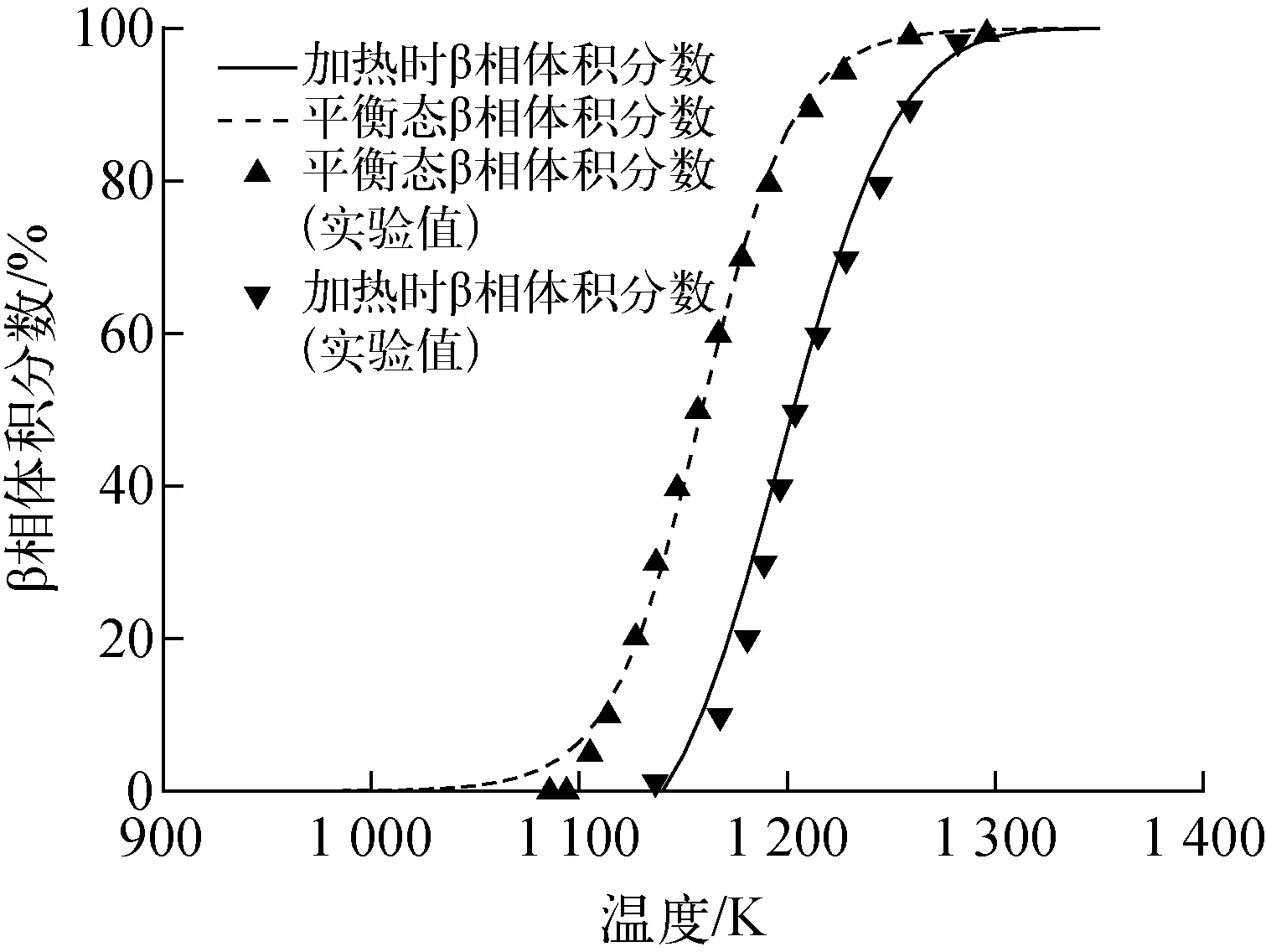
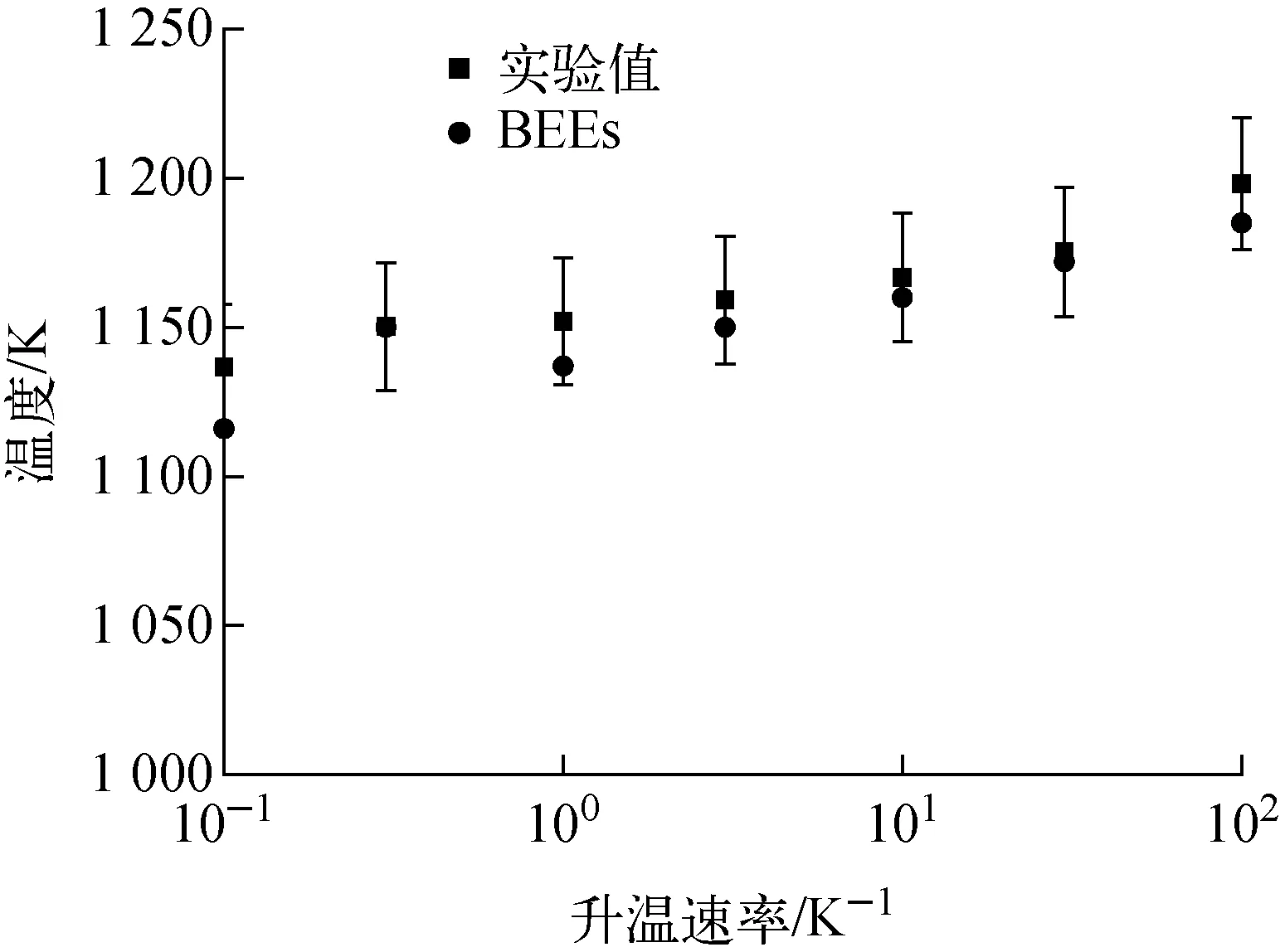
2.3 包壳相变模型验证

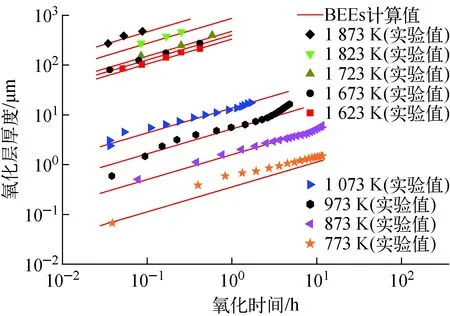
2.4 包壳高温氧化模型验证
3 整体验证分析
3.1 RIA模拟验证

3.2 LOCA模拟验证

4 总结

