基于优化串−并联模型的钢桁拱桥系统易损性研究

刘聪聪，张永亮，汪振新，朱光增

(1.兰州交通大学 土木工程学院，甘肃 兰州730070；2.上海市政设计研究总院集团 第十市政设计院有限公司，甘肃 兰州730030)

钢桁拱桥具有自重轻，跨越能力强等优点，近年来我国在高速铁路和公路领域修建了大量的钢桁拱桥。但是由于我国钢桁拱桥的修建起步较晚，目前相关的抗震研究也不够成熟，相关规范也仅仅给出了部分指导性的设计原则。而基于概率论与数理统计的地震易损性分析，因其能充分考虑地震动的不确定性影响，是目前主流的桥梁抗震分析方法之一。地震易损性是指在不同的地震动强度下，结构反应超过某一规定破坏极限状态的概率。目前桥梁地震易损性分析主要集中在构件易损性分析及系统易损性分析2个方面。ZHONG等[1]以某(156+430+156)m的斜拉桥为背景，研究了桥塔、桥墩、支座、拉索等构件的构件易损性，王晓伟等[2]以某(80+336+80)m的中承式钢桁拱桥为研究对象，分别采用支座位移、墩底弯矩、拱脚立柱的应力为损伤指标研究了该桥的构件易损性。卓卫东等[3]以(40+450+40)m的无推力拱桥为研究对象，研究了盆式橡胶支座和钢筋混凝土交界墩的易损性。但是上述研究均停留在桥梁的构件易损性层面，并没有从桥梁系统层面进行地震易损性研究。PAN等[4]以(30+36+30)m连续梁桥为例，研究了桥墩、支座等的构件易损性，并基于串联模型按照一阶界限法得到了桥梁系统的易损性曲线。WU等[5−6]基于串联模型按照一阶界限、PCM和MONTE-CARLO等方法研究了桥梁结构的系统易损性。宋帅等[7]基于串−并联模型，采用copula法对4×25.5 m连续梁桥进行了系统易损性分析。现有的系统易损性研究表明，目前在进行桥梁系统易损性研究时多把桥梁体系视为串联模型，虽然部分文献采用串−并联模型对小跨径的梁式桥进行了系统易损性研究，但基于串−并联模型的钢桁拱桥的系统易损性研究却相对较少。

1 工程概况及混合有限元模型的建立

1.1 工程概况

某主跨490 m的铁路大跨度提篮钢桁拱桥，拱肋内倾3.65°，拱轴线采用拱轴系数2.0的悬链线，矢跨比1/4.475，采用4片主桁设计，每2片组成1个肋，并通过横杆连成整体。上部梁体采用钢材型号为Q345q的钢箱梁，拱肋及拱上立柱采用Q370q和Q345q带肋钢箱截面，交界墩采用C35混凝土墩建造。如图1所示半桥立面图，从左到右按1号～7号对每排拱上立柱进行排序，每排立柱相距37.2 m。1号～4号拱上立柱每排设2根立柱，每2片主桁上侧放置1根立柱；5号～7号拱上立柱每排设4根立柱，单片主桁上侧放置1根立柱。本桥的场地类别为Ⅱ类，地震动峰值加速度为0.248g，地震动反应谱特征周期为0.45 s，抗震设防等级为Ⅷ度。

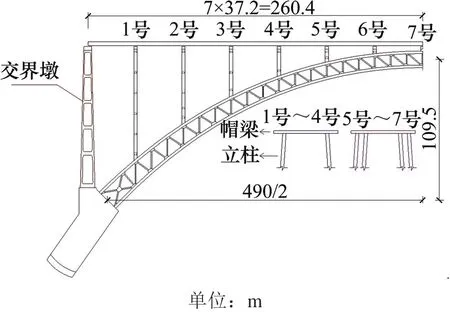
图1 半桥立面Fig.1 Elevation of half bridge

1.2 混合有限元模型的建立

钢桁拱桥结构复杂、杆件众多，地震易损性分析时若所有构件均采用非线性单元，计算及存储代价庞大，因此本文采用弹性梁单元及非线性纤维单元的混合有限元模型。对保持弹性的构件采用弹性梁单元模拟，进入塑性状态的构件采用纤维单元模拟，典型的纤维截面如图3所示，钢材的材料本构采用如图4所示修正的MENEGOTTOPINTO模型，破坏准则采用变形破坏准则。文献[8−9]探讨了混合模型用于地震反应分析的优越性。拱脚及交界墩墩底采用固结约束。立柱帽梁与钢箱梁之间的支座均为固定支座，纵向都是固定，横向有固定、有活动；交界墩与钢箱梁之间的支座均为活动支座，纵向都是活动，横向有固定、有活动；上述支座均采用自由度耦合的方式处理。因易损性统计分析时需要对多条地震记录进行非线性地震反应分析，而不同的地震动引起钢桁拱桥屈服构件的数量和位置也不相同，因此需要针对具体的地震激励，建立与之对应的混合有限元模型。采用Midas/civil软件建立图2所示的混合有限元模型。

图2 有限元动力计算模型Fig.2 Finite element dynamic calculation model

图3 典型纤维截面Fig.3 Typical fiber section

图4 修正的Menegotto-Pinto模型Fig.4 Modified menegotto Pinto model

2 易损性分析方法及其相关参数的选取

2.1 地震易损性分析过程

将增量动力分析(IDA)得到的地震需求除以损伤限值，并将其与地震动强度参数(PGA)绘制于对数坐标系下，然后进行二次曲线回归，求得回归均值λ、回归标准差σ，并利用式(3)计算结构在不同PGA下的损伤超越概率。

式中：a，b，c为二次曲线回归参数；Sr为各离散点对于回归曲线的残差平方和；n为离散点个数。

2.2 损伤指标的选取

文献[10-11]均采用最大应变作为钢结构桥梁的损伤评价指标。本文采用文献[11]中的研究成果，将构件分为3种损伤状态，各级损伤状态及其限值依次为：轻微损伤，εy<ε≤2εy；中等损伤，2εy<ε≤8.4εy；严重损伤，ε>8.4εy，其中εy为钢材的屈服应变。

2.3 强震记录的选取

SHOME等[12]研究表明，基于IDA的易损性分析，选取10到20组地震动，其分析结果就具有较高的精度。以规范[13]规定的设计反应谱为目标谱，从美国太平洋地震工程研究中心(PEER)数据库中选取了15组地震记录(15条水平地震动和相应的15条竖向地震动)，采用顺桥向+竖向地震动激励模式。设计反应谱与实际地震记录的平均反应谱的对比如图5所示。对选取的15组地震记录的PGA进行顺桥向与竖向同比例调幅，调幅步长为0.1g，调幅后用于IDA的顺桥向地震动的PGA为0.1g～1.0g，累计生成了150个非线性时程分析工况。

图5 反应谱拟合图Fig.5 Response spectrum fitting diagram

3 构件易损性分析

本文进行易损性分析时PGA的最大值取1.0g，是因为与梁式桥不同，拱桥具有高度的地基敏感性，而文献[14]指出当PGA=1.0g时，地震烈度达到Ⅹ度，震害现象为：山崩和地震断裂出现，因此1.0g对于背景桥而言已属于最不利PGA。对钢桁拱桥输入15组强震记录，且均将其调幅至1.0g，进行非线性地震反应分析。因为不同地震动引起构件的损伤数量和位置均不相同，所以为了剔除不同地震动引起结构损伤构件的个性表现，本文将易损构件定义为：15条地震记录中均发生损伤的构件(即共同损伤构件)。结构易损构件的位置见图6～7，图中加粗构件为易损构件。由于本桥为提篮拱桥，拱肋内倾，内侧拱肋及立柱受力较大，因此选用损伤较严重的内侧拱肋(U1～U4)及其上方的立柱(C1～C4)，共计8根构件，进行构件易损性分析。

图6 易损构件立面分布Fig.6 Vertical distribution of vulnerable members

构件易损性是系统易损性分析的必要前提，根据150个非线性时程分析工况的计算结果，累计提取了1 200个最大应变数据，将这些数据除以各级损伤状态特征值，拟合成24条IDA曲线。根据24条IDA曲线，进一步得出C1～C4拱上立柱，U1～U4上弦杆的24条易损性曲线。因篇幅限制，本文不再给出上述构件的IDA曲线及易损性曲线。

图7 上平纵联易损构件平面分布Fig.7 Plane distribution of upper horizontal longitudinal vulnerable members

4 桥梁系统易损性分析方法

4.1 主、次要构件的划分原则

《公路桥梁抗震设计规范》(JTG/T 2231−01—2020)[15]规定，在拱桥抗震概念设计时，宜在拱上立柱或立墙端设铰，允许这些部位有一些转动或者变形，而拱肋及桥面系应进行强度验算。欧洲规范[16]规定，恒载和设计地震作用下，拱桥的轴压比高，塑性铰区延性设计不可靠，因此主拱圈最好保持弹性。夏修身等[17]提出了大跨度拱桥抗震设计时主要构件、次要构件的设计原则，并指出主拱肋及主梁应视为主要构件，而拱上立柱在概念设计时可设计为延性耗能构件。综上所述：拱上立柱宜视为次要构件，拱肋、桥面系宜视为主要构件。划分主、次要构件的主要出发点是考虑结构某一构件的损伤或失效对大跨钢桁拱桥的承载能力、震后运营和维修加固的影响程度。从抗震概念设计上讲应控制主要构件的损伤程度，因此对大跨钢桁拱桥结构系统易损性分析时，应合理考虑这一因素。

4.2 可靠度模型的选取

目前用一阶界限法评估桥梁结构的地震易损性时，多把结构视为串联模型，串联模型认为体系中的所有构件重要性相同，无法考虑主要、次要构件的权重，而串−并联模型可以较好地体现主要构件、次要构件在系统易损性中的权重。但是简单的串并联模型，虽然能体现主、次构件的权重，但往往与结构实际的失效模式不符，因此本文提出了优化串−并联模型，既体现主次要构件的权重，又能体现结构真实的失效模式。3种模型的具体解释，如下文所述。

模型1：串联模型。将所有易损构件进行串联，模型1只体现了一种失效模式：结构任一构件损伤，结构失效。模型1的失效逻辑图，如图8所示。

图8 模型1失效逻辑图Fig.8 Model 1 failure logic diagram

模型2：简单串−并联模型。将C1～C4立柱进行简单的并联，组成一个并联组件，然后再和U1～U4弦杆(每根弦杆视为一个串联组件)进行串联，组成简单串−并联模型。模型2体现了2种失效模式：拱肋损伤，结构失效；主梁由于相邻4根立柱全部损伤导致桥面系挠度过大，结构失效。模型2的失效逻辑图，如图9所示。

图9 模型2失效逻辑图Fig.9 Model 2 failure logic diagram

模型3：优化串−并联模型。将相邻2根立柱进行并联，组成3个并联组件(C1和C2，C2和C3，C3和C4)，同理再和U1～U4弦杆(每根弦杆视为一个串联组件)进行串联，组成优化串−并联模型。模型3同样体现了2种失效模式：拱肋损伤，结构失效；但与模型2不同，主梁是当相邻2根立柱损伤导致桥面系挠度过大，结构失效。由于背景桥各排拱顶立柱之间相距37.2 m，相邻2根立柱失效后，桥面挠度已经影响正常使用，所以模型3相比模型2更能真实地代表结构的实际失效模式。模型3的失效逻辑图，如图10所示。

图10 模型3失效逻辑图Fig.10 Model 3 failure logic diagram

4.3 系统易损性公式推导

目前对一阶界限法计算串−并联模型系统易损性的研究较少，因此本文对串−并联模型的计算公式进行详细推导。

1)串−并联模型中所有组件是完全正相关(相关系数ρ=1)时，系统失效的下界值是由失效概率最大的组件决定的。用下标i，j分别代表构件、组件的编号，用下标c，b分别代表串联、并联组件的编号。

系统失效的下界值可表示为：

对于背景桥中的并联组件，其失效概率的下界值Pfb是由并联组件中有构件均失效这一事件决定，其失效概率的表达式为：

因为背景桥的每个串联组件中均只包含一个构件，所以其失效概率Pfc等于串联组件所对应构件的失效概率，其失效概率的表达式为：

2)串−并联模型中所有组件的是相互独立(相关系数ρ=0)时，系统失效概率为所有组件均正常工作的逆事件。系统失效的上界值可表示为：

并联组件的失效概率的下界值Pfb由并联组件中失效概率最小的构件决定，其失效概率的表达式为：

同理，对于串联组件，其失效概率Pfc为：

由于各失效模式间的相关性介于上面2种情况之间，所以串−并联模型失效概率Pf的界限范围为：

式(10)即为串−并联模型系统损伤超越概率上下界的计算公式，该式同样适用于串联模型。

5 系统易损性分析

5.1 钢桁拱桥的系统易损性曲线

根据模型1，2和3分别绘制了背景桥的系统轻微、中等、严重损伤的易损性曲线。系统易损性曲线如图11～13所示。

图11 系统轻微损伤超越概率Fig.11 Exceedance probability of minor damage of system

图13 系统严重损伤超越概率Fig.13 Exceedance probability of serious damage of system

根据图11～13的计算结果，可以得到：

1)采用模型1计算的系统损伤超越概率最大，采用模型2计算的系统损伤超越概率最小，模型3的计算结果基于模型1，2之间。

2)在设计地震(PGA=0.248g)作用下，模型1，2和3的系统轻微损伤超越概率分别在19%～43%，2%～3%，3%～21%之间，中等损伤超越在1%～2%，0，0之间，严重损伤均为0。结果表明：若根据模型1和2进行系统地震易损性评估，则在设计地震作用下拱桥系统发生轻微损伤的概率较高、较低，这与实际情况不符。

3)采用模型2进行系统易损性分析时，系统未出现严重损伤，模型1和3进行系统易损性分析时，系统出现严重损伤。但模型1计算的严重损伤超越概率最大值高达54%，而模型3计算的最大值仅为9%。

5.2 系统易损性差值曲线及损伤控制组件曲线

为进一步比较3种可靠度模型计算的系统易损性曲线的差异，本文绘制系统易损性差值曲线。将模型1的损伤超越概率上、下界减去模型3的损伤超越概率上、下界，记为Δ1；同理将模型3的损伤超越概率上、下界减去模型2的损伤超越概率上、下界记为Δ2。易损性差值曲线如图14～15所示。一阶界限法计算的系统损伤下界是由模型中的损伤超越概率最大的组件决定的，下文将该组件称为：损伤控制组件。为分析不同可靠度模型计算的系统易损性不同的原因，绘制系统损伤下界的损伤控制组件曲线。损伤控制组件曲线如图16所示。

图14 模型1，3系统损伤超越概率差值曲线Fig.14 Difference curves of damage exceeding probability of model 1 and 3 system

图15 模型2，3系统损伤超越概率差值曲线Fig.15 Difference curves of damage exceeding probability of model 2 and 3 system

图16 系统损伤下界控制组件Fig.16 System damage lower bound control unit

根据图12～14的计算结果，可以得到：

图12 系统中等损伤超越概率Fig.12 Exceedance probability of medium damage of system

1)当PGA=1.0g时，Δ1的最大值由严重损伤的损伤上界提供，其值为50%；当PGA=0.8g时，Δ2的最大值由中等损伤的损伤上界提供，其值为96%。结果表明，模型1导致系统严重损伤误差最大，模型2导致系统中等损伤误差最大。

2)当采用模型1时，系统易损性多由损伤超越概率较大的C1，C2立柱控制；当采用模型2时，由损伤超越概率较大的U2，U4弦杆控制；当采用模型3时，由损伤超越概率较大的C1，C2立柱组成的并联组件控制。

6 结论

1)串联模型不适用于主、次构件分明的钢桁拱桥。而简单的串−并连模型，虽然能考虑主、次构件在系统中的权重，但往往不能代表结构的实际的失效模式，而优化串−并连模型能克服上述2种模型的弊端。

2)设计地震作用下，采用根据串联体系、简单串−并连体系进行系统地震易损性评估，分别会高估、低估拱桥系统发生轻微损伤的概率，这与实际损伤程度不符。

3)当PGA=1.0g时，优化串−并联模型的系统易损性上界值为9%，而串联模型高达54%，简单串−并联模型却为0。

4)串联模型导致系统严重损伤误差最大，简单串−并联模型导致系统中等损伤误差最大，上述2种模型与优化串−并联模型的损伤超越概率差值最大分别为50%，96%。

5)3种模型计算系统易损性时，决定系统损伤超越概率的控制组件不同，这是导致不同模型计算的系统损伤超越概率相差较大的直接原因。