单轨火箭橇跨声速试验复杂流动研究

杨依峰，周人歌，吴 乔，张衷之，陈 浩

北京航天长征飞行器研究所，北京 100076

火箭橇试验是采用小型火箭推动，由火箭橇车体搭载试验件，在专用轨道上运行，获得一系列飞行状态参数的动态试验过程[1]。火箭撬试验是航空航天高速飞行器试验过程中的一种重要的地面模拟试验手段，是介于常规风洞试验和真实飞行试验之间的试验方法，其最大特点是可以模拟试验模型所需的速度和加速度。利用这一试验方法，不仅能考核航空航天飞行器整机、部件的性能，也能考核其对高速飞行环境的适应性和可靠性。该试验方法基本涵盖飞行试验，能够考核全尺寸模型，并且可以在轨无损回收模型，以供进一步的分析。此外，火箭撬试验可以通过在地面模拟飞行过程来获得大量数据，并且试验的重复性、操控性和维护性均优于风洞试验。国外发达国家十分重视高速地面火箭撬试验，在20世纪60年代开展了高速火箭撬试验，如美国建立了长达15km的火箭撬试验轨道，开展了高速飞行器试验、高速火箭发动机试验和高雷诺数气动力试验，以及相关的火箭撬专项试验。火箭撬试验如图1所示。

图 1 火箭撬试验

火箭撬技术的优点在于能够模拟较高飞行的动压，能够测试全尺寸飞行器模型；而缺点在于对飞行器流场的模拟存在复杂的地面效应和橇体干扰。国内外对火箭橇复杂流场开展了大量的研究，如国外Praharaj等[2]对火箭橇的稳态流场进行了模拟；Lofthouse等[3]利用数值手段对超声速单轨火箭橇流场进行了研究；Hegedus等[4]对有、无鸭翼的火箭橇结构进行了气动特性计算，得到了火箭橇表面压力分布。国内邹伟红[5]、张传侠等[6]、肖红等[7]采用数值仿真方法对火箭橇复杂流场进行了研究。这些研究主要针对亚声速和超声速火箭橇试验进行流场研究，对跨声速火箭橇复杂流场研究较少。

为此，文章采用CFD方法对跨声速火箭橇试验进行数值仿真，研究试验地面及橇体对火箭橇试验流场的干扰影响。

1 数值方法

采用Navier-Stokes方程作为流动控制方程，其积分形式为

式中：V为控制体体积；为守恒变量矢量；Ω为控制体表面；为通过表面Ω的净通量矢量，包含黏性项和无黏性项；为表面的Ω单位外法向矢量。

控制方程中通量项的离散采用Van-Leer格式，时间离散采用LU-SGS隐式时间推进格式，湍流模型采用SST湍流模型。该方法已经在航空航天飞行器气动设计中得到了广泛应用。

与传统飞行环境流场仿真相比，火箭橇试验流场仿真存在复杂的相对运动关系。火箭橇在地面高速移动时，气流相对橇车存在一定的速度，而相对地面又是静止的，火箭橇试验相对运动关系如图2所示。

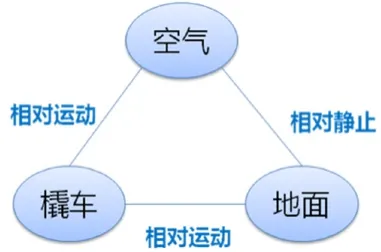
图 2 火箭橇试验相对运动关系

解决该问题比较直接的方法是采用重叠网格技术，地面网格不移动而橇车移动，这需要大量的网格，导致仿真过程相当复杂和耗时。为此，文章基于气流相对条件分析，从物理模型着手，通过边界条件实现对整个运动过程流场的仿真。具体来讲，在假定空气运动的前提下，橇车支架相对空气是运动的，对橇车支架的物面边界信息设定为无滑移边界条件：

u=v=w=0

式中：u、v、w分别为X、Y、Z三个方向的速度；T为温度；n为物面法线方向；w为物面。

试验地面相对空气是静止的，对试验地面的边界信息设定为滑移边界条件：

由此，可以真实地反映火箭橇试验时橇车支架、试验地面与空气之间的相对运动关系，从而能够更加准确地模拟火箭橇跨声速试验时的复杂流动情况。

2 计算模型及网格

文章以某单轨火箭橇为研究对象，试验模型为轴对称球柱外形。单轨火箭橇试验几何模型如图3所示。

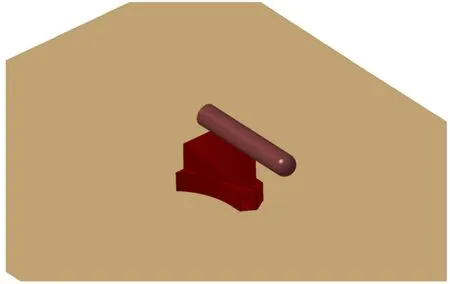
图3 单轨火箭橇试验几何模型

采用非结构混合网格对空间流场进行离散，对模型前缘、激波位置、流动分离区进行网格加密。模型表面网格如图4所示。

图4 模型表面网格

3 结果分析

采用上述方法对火箭橇跨声速流场进行仿真，计算状态为V∞=400m/s。

火箭橇绕流空间压强系数分布云图如图5所示，纵向对称平面压强系数分布云图如图6所示。从图5、图6可以看出，火箭橇前部形成了两处较强的弓形激波，一处位于试验模型前部，另一处位于橇体前部。两道弓形激波在靠近试验地面附近与地面形成了较强的耦合干扰。试验件模型上下的激波形状不同，其激波后的流动存在非对称性，对试验模型的气动特性存在一定影响。

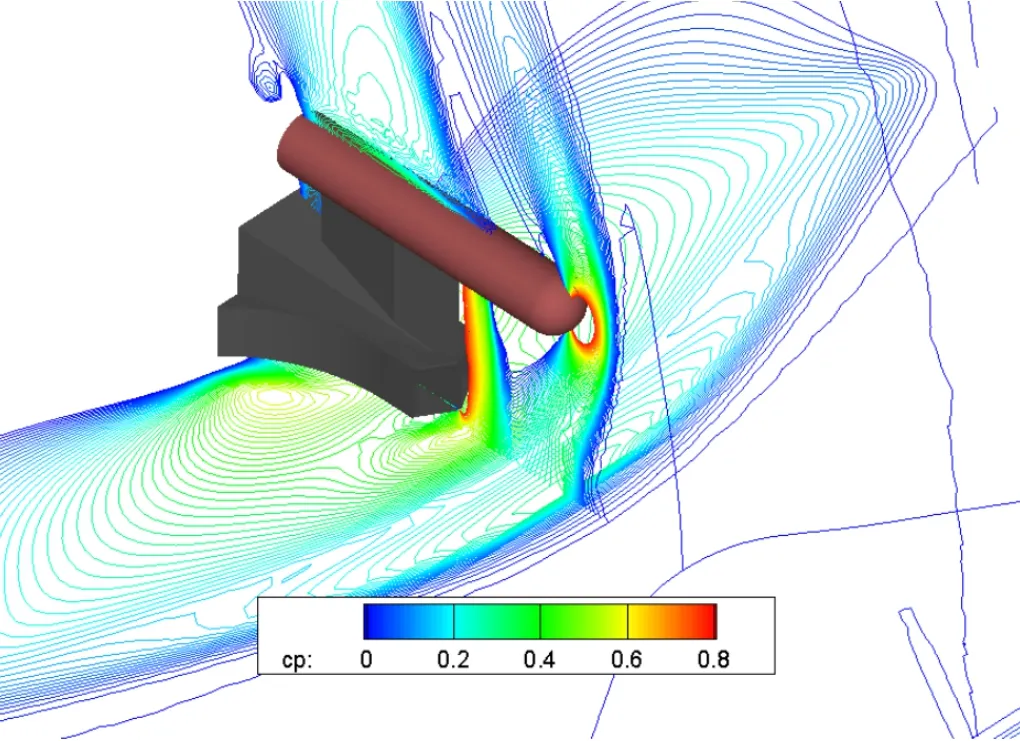
图5 空间压强系数分布云图

图6 纵向对称面压强系数分布云图

火箭橇速度从300m/s至500m/s（间隔50m/s）的纵向对称面压强系数云图如图7所示。从图7可以看出，在速度较低时，试验地面及橇体对试验流场有较大干扰影响；随着速度的增大，橇体前部的弓形激波后移，橇体与试验地面对模型的干扰影响逐渐减小。

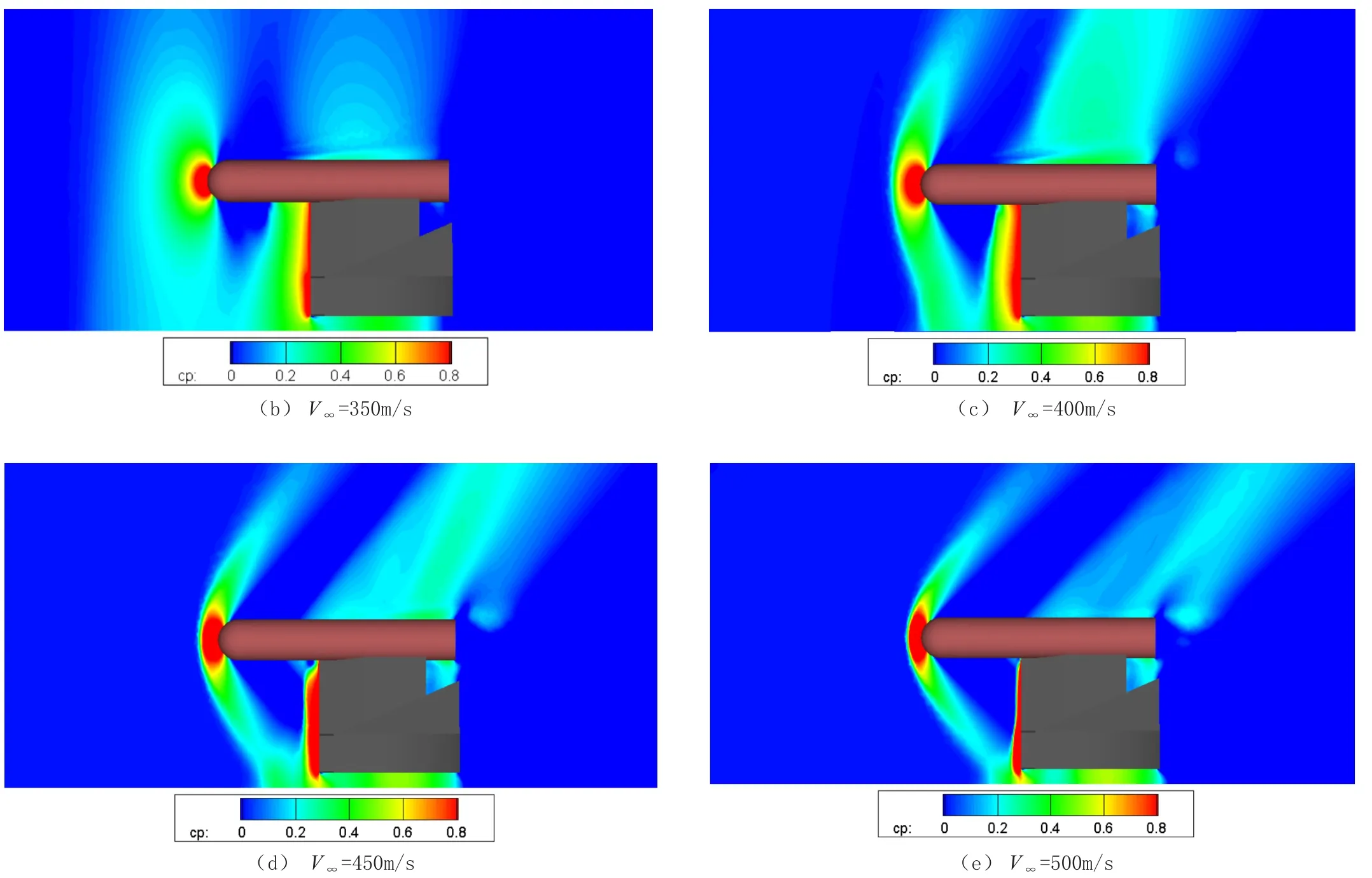
图7 火箭橇不同速度纵向对称面压强系数云图

4 结论

文章采用CFD方法对跨声速单轨火箭橇试验流场进行了研究，主要得出了以下结论：

（1）试验模型前部弓形激波与橇体激波在试验地面附近形成复杂的激波干扰，使试验模型上下流场非对称，对模型气动特性造成干扰影响；

（2）随着橇车速度的增大，橇体前部的弓形激波后移，对模型的干扰影响逐渐减小。