快捷货运电力机车抗蛇行减振器关键参数优化分析

王超，王开云，凌亮

（西南交通大学 牵引动力国家重点实验室，四川 成都610031）

为保证经济快速发展需求，我国大力投资铁路建设。一般采用增大列车编组、增大货车轴重、增大发行密度等方式提高铁路货运量，凭借铁路运量大、运输经济成本低等特点占据市场优势，但近年来铁路的重点运营方向主要围绕增大运输量的重载铁路，忽略了新兴增长经济方式对货物运输速度的要求。随着我国经济发展与电商行业的兴起，具有高时效要求及高附加价值的货物运输量急剧增长，为提升铁路竞争力、提高经济效益，开行快捷货运势在必行[1-2]。快捷货车运行速度的大幅提高对车辆轮轨相互作用提出较大挑战，我国已对160 km/h速度等级的快捷货运列车开展了大量研究，刘林[3]对我国某型快捷货车转向架悬挂参数开展优化研究，实现货车轮轨低动力作用优化设计；韩正彦[4]基于刚-柔耦合动力学仿真模型开展快捷货车转向架焊接结构载荷疲劳评估，为快捷货车的研制与试行提供了理论支撑；奉友勤[5]对160 km/h内侧悬挂转向架的轻量化与轮轨低作用设计开展相关研究。快捷货运列车的提速对快捷货运电力机车转向架的参数设计与优化也必然提出新的要求[6]。现役货运机车设计最高运行速度为120 km/h，难以满足快捷货运列车高速运行的需求，此外还需考虑到现役货运机车所存在的牵引速度较低、运输周期长等问题。转向架构架是机车主要承载和传递载荷的部件，是大多数部件连结的主体骨架，同时也承受着复杂的相互作用力，应具备良好的抗疲劳品质及优秀的动力学性能。机车转向架通常安装横向减振器与抗蛇行减振器[7]以保证车辆运行的安全性与平稳性，而如何优化转向架悬挂系统参数以降低轮轨低动力作用是转向架设计工作的重点。

国内外学者对转向架悬挂参数优化做了大量研究。王开云等[8]基于车辆-耦合动力学理论，以临界速度为优化目标，分析一系悬挂刚度和转向架轴距对“天梭号”机车运行稳定性的影响；吕凯凯等[9]针对新型200 km/h八轴客运机车二系悬挂刚度进行优化分析；刘永强等[10]采用归一化方式建立优化目标函数，分析悬挂系统刚度与阻尼对车辆动力学性能的影响；MOUSAVI等[11]选取磁流变半主动抗蛇行减振器阻尼特性等参数开展研究，采用SIMPACK/MATLAB联合仿真优化车辆动力学性能；ALONSO等[12]从减振器内部结构组成与特性参数方面建立详细的减振器模型，对车辆动力学稳定性进行分析；周素霞等[13]考虑抗蛇行减振器常见故障对高速列车动力学性能的影响；孙建锋等[14]利用简化的抗蛇行减振器Maxwell模型，推导线性临界速度解析表达式，为参数优化提供理论依据。

快捷货运列车研制中须充分考虑客货共线运行工况与现有货运线路运行特性。高速运行工况与货运线路小半径曲线往往难以避免，对车辆运行平稳性提出了新的要求。二系悬挂系统中的抗蛇行减振器对车辆运行稳定性具有较大的影响。本文基于车辆动力学理论，选取抗蛇行减振器为研究对象，建立快捷货运电力机车动力学模型，充分考虑其中的非线性因素，分析节点刚度和阻尼对机车动力学性能与轮轨磨耗的影响，以期为快捷货运电力机车的研制与动力学性能提升提供参考。

1 快捷货运电力机车动力学模型

1.1 机车动力学模型

本文根据快捷货运电力机车的具体结构，建立机车的动力分析模型，如图1所示。车辆动力学模型主要参数如表1所示。机车模型由一个车体、两个构架、两个牵引杆、六个牵引电机、十二根电机吊杆和六个轮对组成，共计174个自由度。该转向架采用C0-C0轴式，牵引电机顺置，驱动单元的悬挂采用弹性架悬方式，电机一端通过单个橡胶关节悬挂于构架端梁，另一端通过两根吊杆悬挂于构架端梁；一系悬挂系统由单拉杆轴箱定位与螺旋弹簧组成，且一、三轴安装垂向减振器；二系悬挂系统由圆螺旋弹簧与橡胶垫结构组成；牵引装置采用低位推免牵引杆牵引方式。采用Kalker非线性蠕滑理论处理轮对和钢轨间的接触力与蠕滑力。

表1 动力学模型主要参数

图1 车辆动力学模型

1.2 减振器等效参数化模型

本文采用等效参数化方法建立减振器模型，将减振器抽象为具有力学特性的典型物理元件组合，采用弹簧-阻尼串联的Maxwell模型模拟抗蛇行减振器，如图2所示。

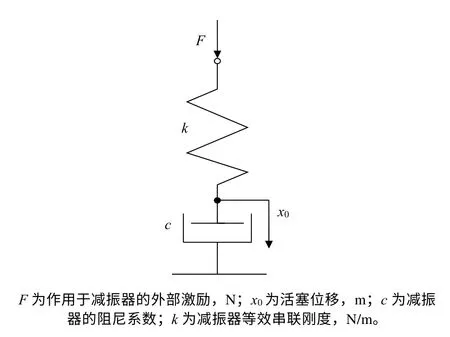
图2 减振器弹簧阻尼串联模型

Maxwell模型的振动微分方程为：

式中：x为减振器橡胶节点位移，m。

将外部激励F=Asin(ωt)代入式（1），整理可得：

式中：ω为固有频率，rad/s；φ为初相位，rad；A为振幅；t为时间，s。

减振器活塞速度可由式（2）直接求解：

减振器阻尼力为：

由式（2）与激励F对比可知，考虑减振器串联刚度时，激励与阻尼力之间产生相位滞后现象，阻尼力幅值相应减小，变为理想阻尼力的倍，当节点刚度增加时，阻尼力幅值也随之增加，即橡胶节点刚度的变化对减振器的阻尼特性有较大影响，对车辆的动力学性能产生明显影响[15]。抗蛇行减振器阻尼为非线性阻尼，本文以原阻尼特性作为标准阻尼特性曲线，对该标准阻尼特性曲线取百分比偏差值作为阻尼变化条件，如图3所示，根据抗蛇行减振器关键参数k、c的变化分析对机车动力学性能的影响。

图3 抗蛇行减振器阻尼特性曲线变化条件

2 评价指标

抗蛇行减振器对车辆的横向稳定性具有较大的影响，本文选取轮轨横向力与磨耗指数作为评价指标，对减振器关键参数进行优化分析。

国内外学者提出多种磨耗指数的计算方法，在一定程度上反映轮轨间的磨耗情况[16]。传统磨耗指数为Heumann磨耗指数，该指数是目前应用最为广泛的简化磨耗指数模型，但该计算方法忽略接触点具体位置，无法反映不同轮轨廓形对磨耗的影响，且轮轨磨耗与轮对冲角成线性关系的描述与实际情况不符；Marcotte磨耗指数计算方法体现轮轨两点接触位置，但实际应用中需计算轮轨空间接触位置，计算量与误差均较高。英国铁路在非线性曲线通过研究的基础上，通过对轮轨接触面上能量耗散理论分析和试验测定，提出以轮轨接触斑处所消耗摩擦功作为轮轨评价指标，忽略自旋蠕滑的影响，即为Elkins磨耗指数：

式中：xF、yF分别为纵向、横向蠕滑力，N；xε、yε分别为纵向、横向蠕滑率。

英国Deby研究中心和北美铁道协会运输试验中心所进行的现场试验[17]证实了轮轨磨耗与接触斑处所消耗功有较好的线性关系，能较为准确地反映轮轨磨耗规律。因此，本文针对磨耗方面选取Elkins磨耗指数作为评价指标。

3 抗蛇行减振器关键参数影响分析

3.1 直线工况结果分析

直线工况设置快捷机车以160 km/h速度通过直线段，轨道不平顺为美国六级谱。考虑导向轮对磨耗指数较高，而第三位轮对磨耗指数远低于前两位轮对，本文对机车第一、第二位轮对计算结果进行分析，其中磨耗指数分别选取最大值与均方根（有效值）开展分析。

抗蛇行减振器节点刚度变化对轮轨横向力与磨耗指数的影响如图4所示。

图4 抗蛇行减振器节点刚度对动力学指标的影响

节点刚度在10～20 MN/m时，第一位轮对的轮轨横向力呈减小趋势，节点刚度高于此范围时，第一位轮对的轮轨横向力迅速增大，直至节点刚度达到60 MN/m后趋于平缓。第一位轮对在20 MN/m时轮轨横向力为23.86 kN，在10 MN/m与30 MN/m时轮轨横向力分别为27.15 kN与32.4 kN，分别降低12%与26%。第二位轮对在10 MN/m时轮轨横向力最低，当节点刚度由10 MN/m增长至20 MN/m时，第二位轮对轮轨横向力急剧增加，之后随着节点刚度的增长，第二位轮对轮轨横向力始终在30～35 kN范围内波动。第二位轮对磨耗指数最大值与两轮对的磨耗指数有效值均随抗蛇行减振器节点刚度的增长呈不断增长趋势，而第一位轮对磨耗指数最大值变化趋势与轮轨横向力变化趋势较为接近，在节点刚度由10 MN/m增长至30 MN/m范围内呈现先降低后增长的趋势。第二位轮对在刚度50 MN/m时虽也具有较低的轮轨横向力，但其磨耗指数最大值与有效值均有所提升。

直线工况轮轨横向力与磨耗指数随抗蛇行减振器阻尼变化的结果如图5所示。可以看出，在抗蛇行减振器阻尼特性比值从50%增长至150%的过程中，第一位轮对轮轨横向力与第二位轮对轮轨横向力均呈明显的“降低－增长”趋势，其中第一位轮对轮轨横向力在120%比值处为最低值，而第二位轮对轮轨横向力在100%比值时处于最低值；第一位与第二位轮对磨耗指数最大值变化趋势与轮轨横向力较为接近，而两轮对的磨耗指数有效值均呈现逐渐降低的趋势，且阻尼特性比值在120%～150%时，第一位与第二位轮对磨耗指数有效值数值趋于一致，转向架前两位轮对趋于均匀磨耗状态。

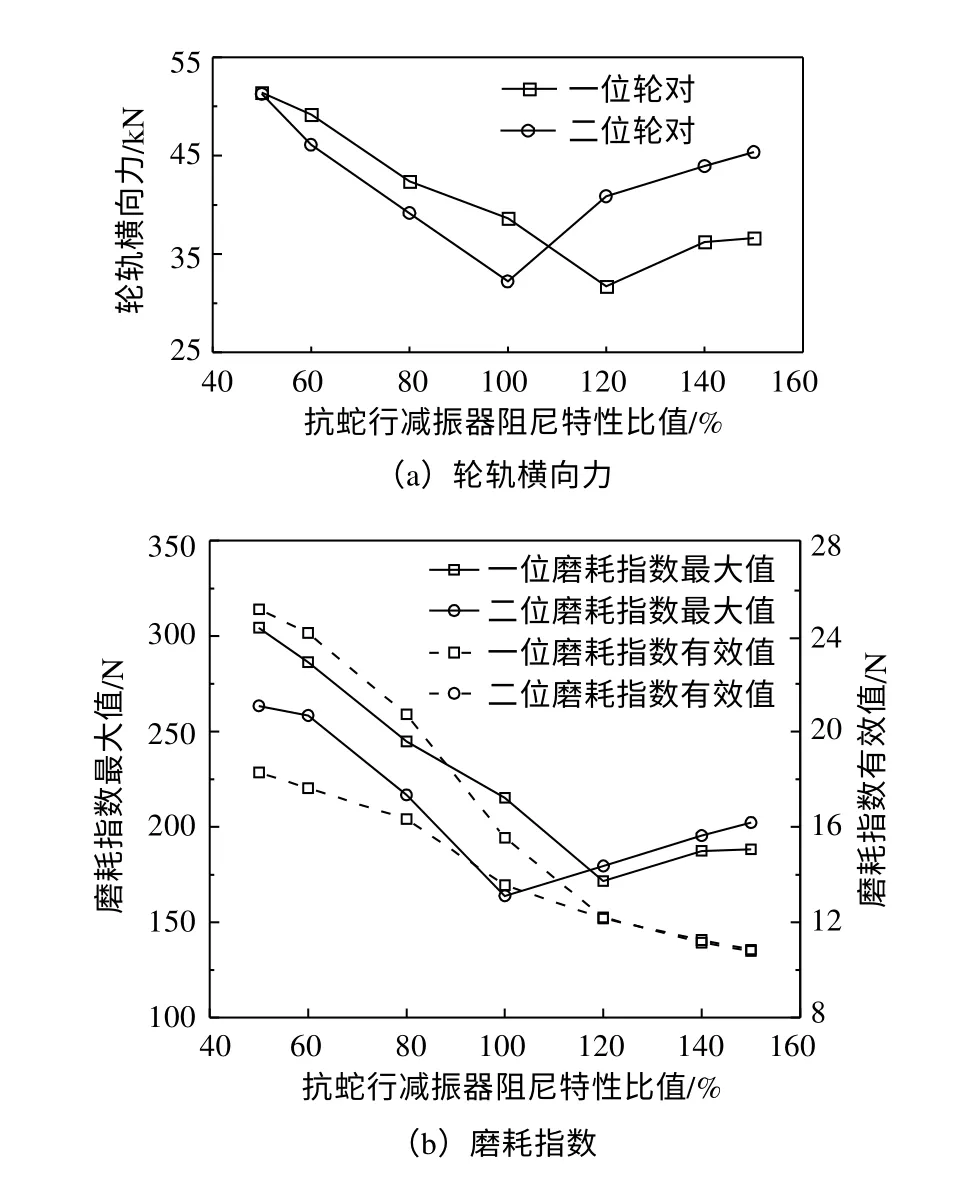
图5 抗蛇行减振器阻尼特性对磨耗指数的影响

3.2 曲线工况结果分析

快捷货运列车主要开行线路为提速线路，本文选取提速线路2200最小半径曲线，设置运行速度140 km/h，超高设置均衡超高，轨道不平顺为美国六级谱，计算结果仅考虑缓和曲线和圆曲线段。轮轨横向力随抗蛇行减振器节点刚度的变化如图6所示。相较直线工况的变化幅度，曲线工况两个轮对轮轨横向力的变化趋势均为平缓增长，而节点刚度处于10～30 MN/m范围内增长时，第二位轮对轮轨横向力呈先降低后增长的趋势。

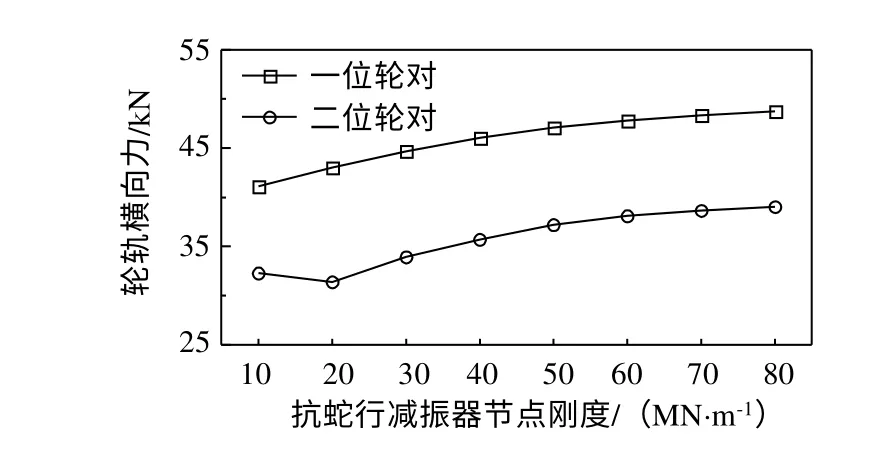
图6 抗蛇行减振器节点刚度对轮轨横向力的影响

磨耗指数随节点刚度变化的结果如图7所示，曲线工况内转向架导向轮对在轨道上经由纵向蠕滑力产生偏转力矩，提供转向架的自导向作用，因此第一位轮对的磨耗指数最大值与有效值远大于第二位轮对。第一位轮对磨耗指数最大值随节点刚度的增大呈一定的增长趋势，节点刚度由10 MN/m增长至20 MN/m时，磨耗指数最大值分别为327.73 N与332.14 N，增长较为平缓，且第一位轮对磨耗指数有效值在节点刚度20 MN/m时取得较低值。当节点刚度从20 MN/m增长至80 MN/m时，第一位轮对的磨耗指数最大值与有效值均明显增长。第二位轮对磨耗指数最大值随节点刚度的增长呈先降低后增长的趋势，而其磨耗指数有效值始终保持增长趋势。

图7 抗蛇行减振器节点刚度对磨耗指数的影响

轮轨横向力随阻尼特性比值变化的结果如图8所示，随着抗蛇行减振器阻尼特性比值的增加，第一位轮对与第二位轮对的轮轨横向力变化规律并不一致，第一位轮对的轮轨横向力先增大后降低，第二位轮对的轮轨横向力波动较大，呈现“降低－增长－降低”的趋势。第一位轮对轮轨横向力随阻尼特性比值的增大呈先增长后降低的趋势。

图8 抗蛇行减振器阻尼特性对轮轨横向力的影响

阻尼特性比值变化对磨耗指数的影响规律如图9所示。第一位轮对磨耗指数最大值变化规律与轮轨横向力一致。第二位轮对磨耗指数最大值在50%～100%比值内迅速降低，在阻尼特性比值从100%增长至150%范围内磨耗指数最大值趋于平缓。第一位轮对与第二位轮对磨耗指数有效值随阻尼特性比值的增长均呈一定的降低趋势。

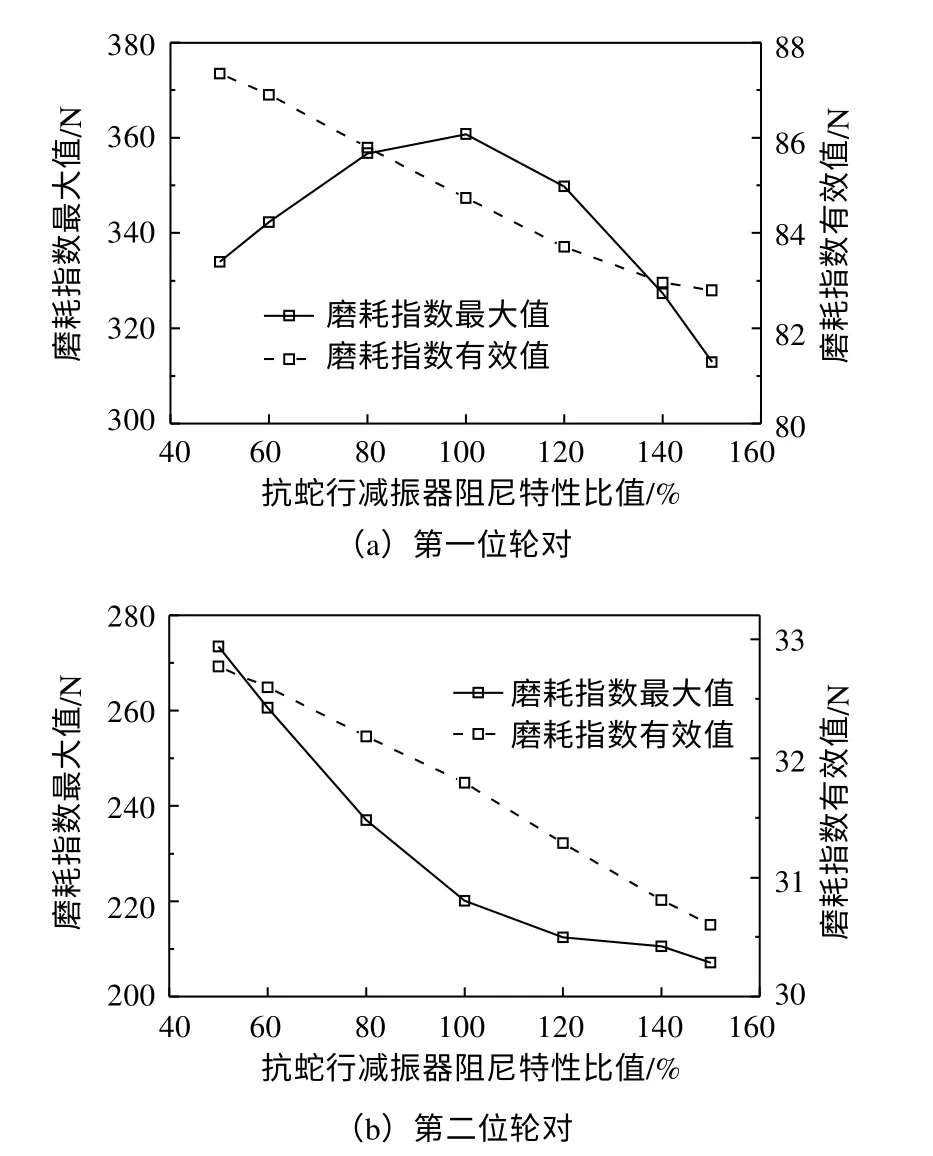
图9 抗蛇行减振器阻尼特性对磨耗指数的影响

3.3 优化参数对比分析

直线工况与曲线工况仿真计算结果表明，当抗蛇行减振器节点刚度处于20 MN/m、阻尼特性比值为120%时，快捷货运机车的轮轨横向力与磨耗指数均处于较优值，故采用上述节点刚度与阻尼特性比值参数开展仿真计算，优化前后机车前转向架相关参数的数值变化情况如图10所示。采用优化参数后，直线工况轮轨横向力最大值为35.31 N，相较原参数降低9%，磨耗指数最大值与有效值分别为152.49 N和8.81 N，相较原参数分别降低29%和43%；曲线工况轮轨横向力最大值为41.31 N，较原参数降低11%，磨耗指数最大值与磨耗指数有效值分别为314.03 N和81.13 N，较原参数分别降低13%和4%。

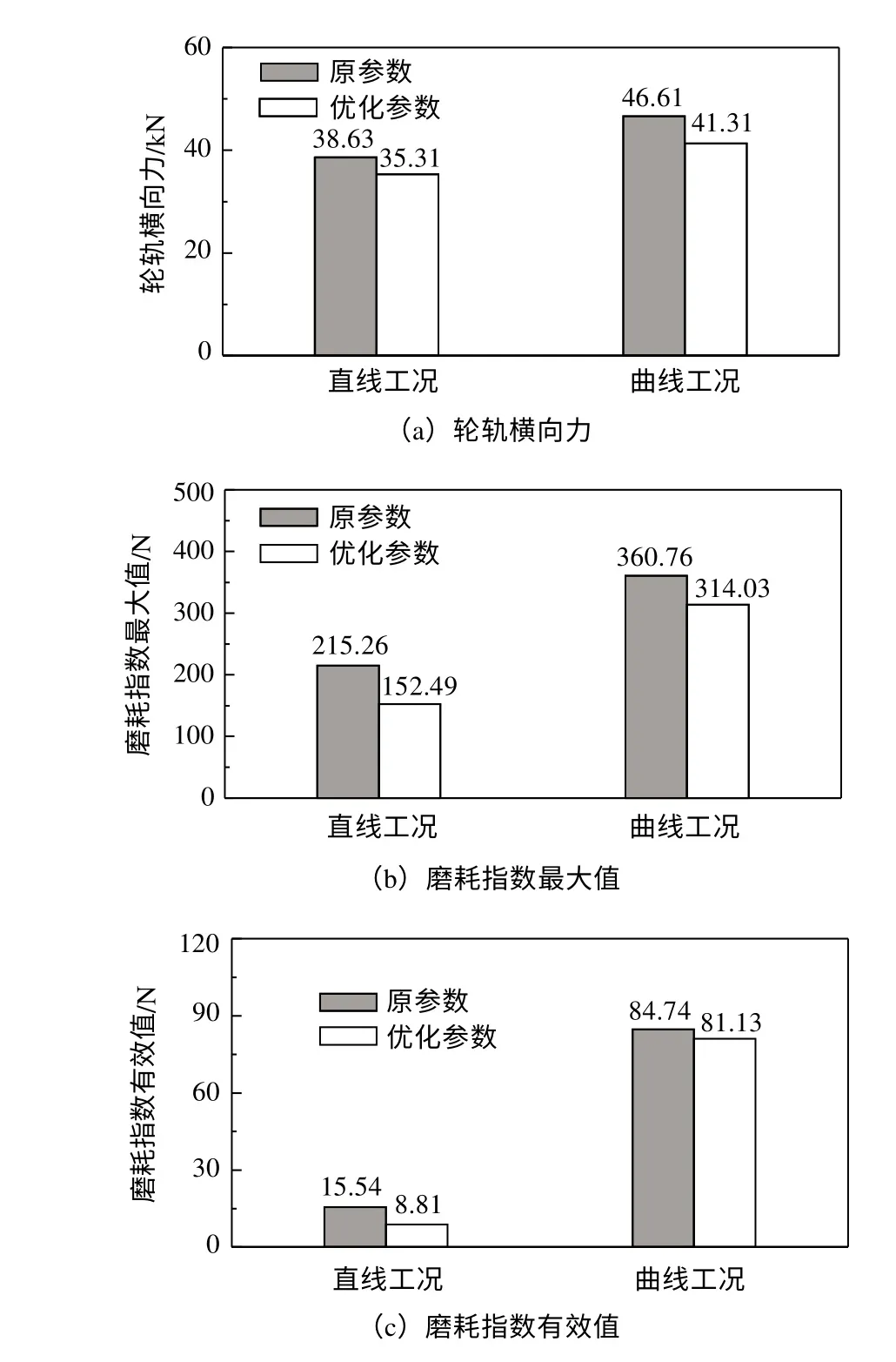
图10 抗蛇行减振器优化参数对比分析

4 结论

本文基于多体动力学软件SIMPACK建立快捷货运电力机车动力学模型，从轮轨横向力与磨耗指数两个角度，分析抗蛇行减振器关键参数对机车运行性能的影响，并提出了抗蛇行减振器关键参数的优化建议。主要结论如下：

（1）在轮轨横向力方面，当抗蛇行减振器节点刚度处于10～30 MN/m时，轮轨横向力增长程度较为明显，随着抗蛇行减振器刚度逐渐增长，轮轨横向力的增长趋于平缓，较低的阻尼比值亦会加剧轮轨横向作用。

（2）在磨耗指数方面，抗蛇行减振器节点刚度越大，磨耗指数最大值与有效值越大。另外，磨耗指数有效值始终随抗蛇行减振器阻尼比值的增大而降低。

（3）抗蛇行减振器节点刚度与阻尼对车辆运行性能均有影响。理论分析结果表明，抗蛇行减振器节点刚度的优化值为20 MN/m、最优阻尼特性为120%标准阻尼特性，即当抗蛇行减振器卸荷速度0.01 m/s、卸荷力15.6 kN时，机车轮轨横向力与磨耗指数达到相对最优状态。与原参数相比，直线工况与曲线工况轮轨横向力分别降低9%和11%，磨耗指数最大值分别降低29%和13%，磨耗指数有效值分别降低43%和4%。