基于FLAC3D煤层底板扰动规律的数值模拟研究
田 磊,田豪杰,殷德耀
(1.河南省有色金属地质矿产局第二地质大队,河南 郑州 450016;2.河南省有色金属矿产探测工程技术研究中心,河南 郑州 450016;3.河南理工大学 资源环境学院,河南 焦作 454000 4.河南省有色金属地质矿产局第三地质大队,河南 郑州 450016)
0 引言
我国煤炭开采目前已经进入深部开采阶段,煤层底板突水事故层出不穷[1],严重影响着矿井的安全生产[2],成为制约我国煤炭资源开采的巨大障碍[3]。弱的底板岩性往往是巷道变形破坏的起始部位[4],大量的研究结果表明,底板破坏是造成突水事故发生的重要原因。无数国内外学者对底板突水机理进行了科学研究,模拟实验是研究煤层工作面导水机制的有效方式之一[5-8],近年来,我国学者对煤层底板扰动规律的研究取得了更大的进步,周扬[9]采用FLAC3D数值模拟软件,结合多元非线性回归分析理论,分析不同破坏因素对煤层底板破坏深度的影响程度。李春元[10]运用离散元软件分析了不同采深下扰动地板的应力变化和变化破坏行为,得到了深部开采底板的扰动破坏分区特征。李昂等[11]通过数值模拟分析,建立了底板岩体扰动破坏深度公式,为本次研究提供了科学指导。FLAC3D(Fast Lagrangian Analysis of Continua)是一款仿真计算软件,在工程领域方面应用广泛[15-17],通过综合运用混合-离散分区技术与拉格朗日算法,可以在很小内存空间里解决大范围的三维问题。FLAC3D数值模拟精度高,操作便捷,对煤层底板扰动规律的研究具有十分重要的意义。为了更好的研究煤层底板扰动规律,本文通过运用数值模拟的方法进行研究,探究煤层采动过程中的底板扰动规律。
1 工程背景
贺驼煤矿地处河南省鹤壁市与安阳市交界处,南邻鹤壁,北接安阳。矿区南北长约2.7 km,东西宽1.0~2.1 km,面积3.1272 km2,本矿现在-300 m开采水平11采区进行开采,现有5个回采工作面,开采高程为-350 m~-450 m。在开采范围内,煤层厚度为3.58~9.36 m,一般厚度约为7 m,煤层倾角10°~20°。地层总体走向近南北,倾向NE,倾角2°~30°。构造以断裂为主,伴有小型褶曲。
矿井煤层的开采活动会破坏煤层底板岩层的应力状态,使围岩失去支撑进而逐渐移动,破坏采空区,形成的裂隙易发生突水。贺驼煤矿煤层承压水压力大,且矿井内构造发育丰富,严重破坏了煤层底板隔水层稳定性,威胁着矿区的生产安全。
2 模型建立
FLAC3D数值分析软件被广泛应用在我国岩土和地质工程领域,其原理是基于拉格朗日法通过显示有限差分来模拟三维连续介质的力学行为进而获得模拟对象的力学响应数值。该软件将空间模型等效为一个空间四面体单元,在四面体的各个面上进行模型的模拟计算。同时四面体单元的网格节点代表单元体力的分布,并通过时域运动方程动态求解,达到设计精度,最终输出模拟计算结果。
模型开挖之前,需要确定模型是否处于平衡状态。通常情况下,只要模型网格顶点最大不平衡力与平均值的比值不小于10∶1,就表明所建立的模型处于平衡状态。此外,还需对模型进行位移归零处理,以保证模型的垂直位移变化是由开挖所引起的。根据矿井地质资料和研究区岩石实验结果,得到岩石物理学参数(表1),建立长、宽、高分别为400 m、600 m、230 m的空间数值模型。正常模拟的情况下,将煤层上部的岩层看作是一个重块,重块的密度取决于岩层的平均密度,此外再根据岩层的厚度和密度计算重块的压力值。岩层的自重应力方向见图1。在设定边界条件时,将X方向(倾向方向)、Y方向(走向方向)、Z方向(重力方向)以及模型底部设置为固定边界(图2)。模拟过程中,煤层顶底板位置固定不变,在对破坏深度进行计算时,以煤层顶底板为边界进行计算。在模拟过程中,为更好地观测煤层顶底板垂向位移、底板岩体竖向压力、顶底板塑性区的破坏范围以及变化规律,在建立三维模拟模型时将局部网格细化。本次模拟共分20次开挖,每次开挖步距均为10 m。模拟模型结构图见图3。

表1 模拟地层的平均厚度及岩石的物理力学参数Table 1 The average thickness and physical and mechanical parameters of the simulated rock layer

图1 岩石的自重应力示意图Fig.1 Schematic map of the gravity stress of rock layer

图2 模型边界条件图Fig.2 Boundary condition map of the model

图3 模拟模型结构图Fig.3 Structural map of the simulation model
岩体自重应力的计算公式表示如下:
σz=γH
式中:σz为岩体的自重应力,MPa;γ为岩体的平均容重,kN/m3。
根据广义胡克定律可知:
εx=1/E[σx-μ(σy+σz)]=0,
εy=1/E[σy-μ(σx+σz)]=0,
σx=σy=μ/(1-μ)σz=μ/(1-μ)γH。
式中:εx、εy为岩石的横向变形量;μ为岩石的泊松比;E为岩石的弹性模量,Pa。
综合上式可以得出:σx=σy=μ/(1-μ)σz。
令侧压系数为λ,即:λ=μ/(1-μ),则:σx=σy=λσz。其中λ取值由岩石本身力学性质及应力状态所决定,大小介于0.8至1.2。
3 数值模拟及结果分析
3.1 底板垂直应力分析
随着工作面开采活动的不断推进,打破了煤层底板的原始应力平衡状态。应力重新分布时,由于底板围岩的强度有限,会造成煤层底板产生新的破坏。通过分析每次模型开挖后的应力分布,就能得出一定的应力分布规律。
通过进行数值模拟,得到煤层工作面中间部位应力云图,对煤层底板垂直应力的分布规律进行分析。由图4可见,在开采活动的影响下,采空区两端出现应力集中现象,其竖向应力值相对较大。沿煤层走向方向,垂向应力呈左右对称状分布。随着工作面的逐步推进,煤层顶底板应力增大,采空区压力减小,底板岩层应力状态由压缩变为膨胀。整体上会随开采区域的扩大而形成一个应力拱,应力拱中部垂向应力值相对较小。

图4 工作面不同采掘长度垂直应力分布图Fig.4 Vertical stress distribution diagram for the different mining lengths of work face1—掘进巷道 2—垂直应力
3.2 底板破坏特征分析
3.2.1 底板走向方向破坏特征
在煤层的开采过程中,底板破坏深度底板岩性等因素的影响。由于岩层受到破坏,在采空区底板处可能会形成底鼓现象,威胁开采活动的进行。对工作面模型走向上破坏区域结果进行分析,煤层底板走向方向破坏深度分区图见图5。
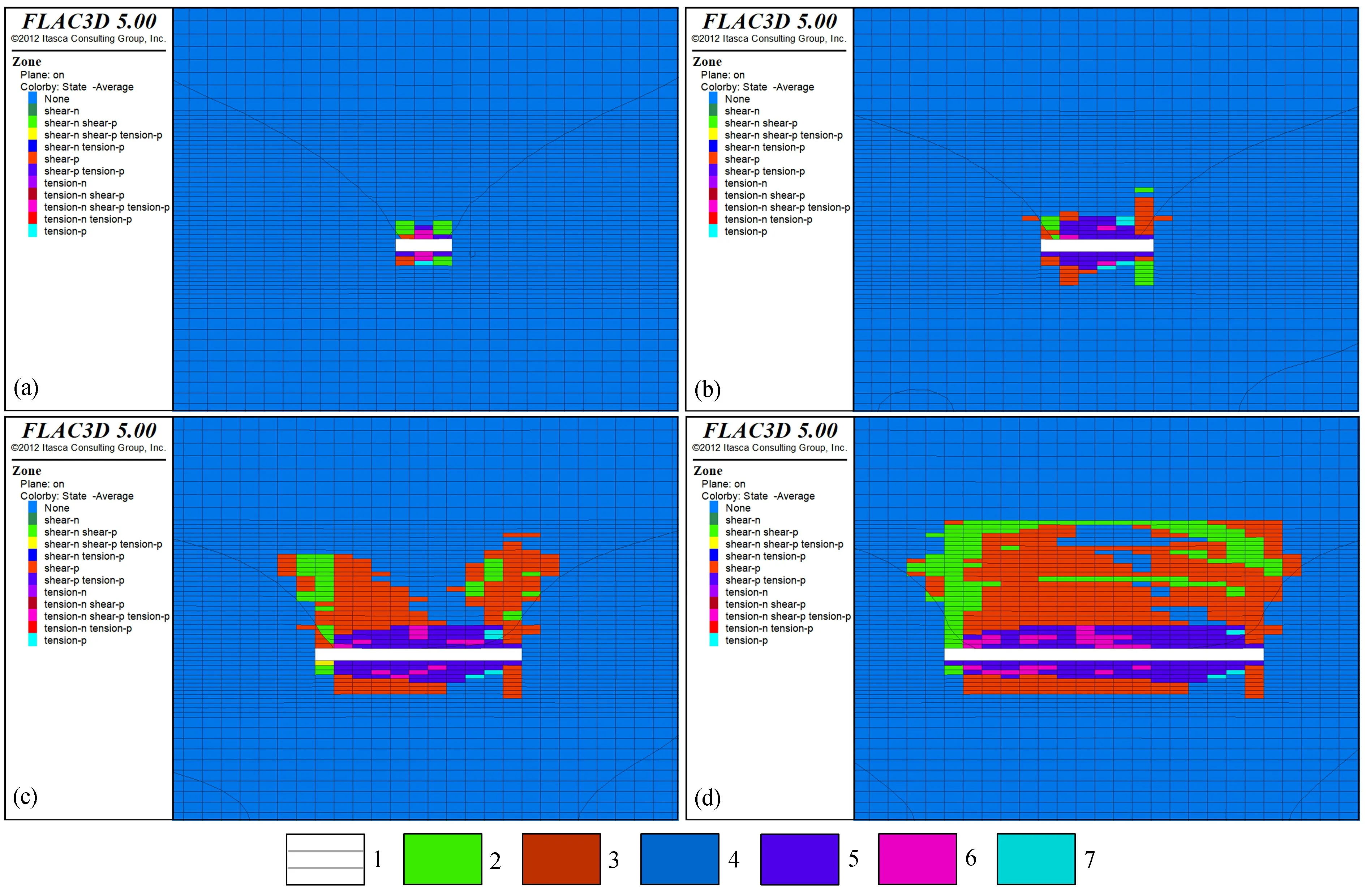
图5 不同掘进深度煤层底板方向受力分区图Fig.5 The stress distribution map of coal seam floor in the striking direction for the work face of different tunnel lengths (a)工作面掘进30 m (b)工作面掘进60 m (c)工作面掘进110 m (d)工作面掘进170 m1—掘进巷道 2—剪应力 3—剪应力 4—不受力 5—混合应力 6—混合应力 7—张应力
从煤层走向方向来看,随着工作面的推进,煤层底板发生剪切破坏,煤层工作面推进距离为30 m时,煤层顶底板开始发生塑性破坏;当工作面推进到110 m时,煤层底板达到了最大破坏深度22.41 m;之后底板破坏深度则不再随着工作面的推进而变化,最终趋于稳定,破坏范围随着工作面的继续推进继续扩大。
3.2.2 底板倾向方向破坏特征
为了对倾斜煤层倾向上下端的不同进行更直观的对比,取工作面步距推进至100 m、130 m、150 m和170 m处工作面底板倾向方向破坏区域图见图6。
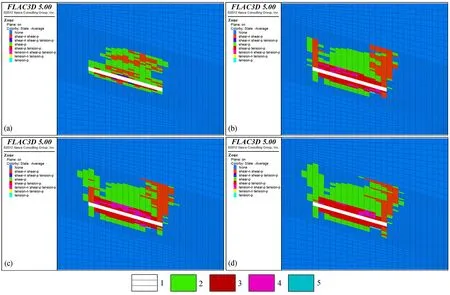
图6 不同掘进深度煤层底板方向受力分区图Fig.6 The stress distribution map of coal seam floor in the dipping direction for the work face of different tunnel lengths (a)工作面掘进100 m (b)工作面掘进130 m (c)工作面掘进150 m (d)工作面掘进170 m1—掘进巷道 2—剪应力 3—混合应力 4—混合应力 5—张应力
分析可知,煤层底板主要受到剪切破坏,采空区部分煤层底板会受到拉伸破坏的作用。开采过程中随着工作面的不断推进,煤层底板倾向方向上的破坏深度由12 m增加至18 m,且主要位于采空区中部。破坏高度也在不断增加,但在工作面开采推进至150 m处时,煤层底板的破坏深度达到最大并且不再随工作面开采掘进而增加。由此可知,煤层底板的破坏位置没有发生大的偏移。
4 结论
1)随着开采活动的进行,采空区两端出现应力集中现象,其竖向应力值相对较大。煤层顶底板应力增大,整体上会随开采区域的扩大而形成一个应力拱,应力拱中部垂向应力值相对较小。
2)随着工作面的推进,底板破坏程度逐渐增大,推进到一定程度,底板采动破坏深度达到最大,之后趋于稳定,而破坏范围一直在增大。当工作面推进至110 m时,底板采动破坏深度达到最大值22.41 m。
3)煤层底板主要受到剪切破坏作用,部分采空区煤层底板会发生拉伸破坏,煤层底板破坏位置没有发生偏移。

