基于球杆仪的数控机床几何误差辨识与建模

杨洪涛 张宇 李莉 马群 汪珺

摘 要：針对现有激光干涉仪的数控机床几何误差辨识与建模，操作过程复杂、建模效率低等问题，提出了一种新的基于球杆仪的数控机床几何误差辨识与建模方法。利用三平面圆弧轨迹测量法和球杆仪对误差进行测量，建立了球杆仪读数与机床各平面内对应几何误差之间的辨识模型，实现了几何误差辨识，并建立了机床综合误差预测模型。同时利用激光干涉仪建立比对实验装置，测量出机床的实际几何误差。分别将利用球杆仪辨识出的几何误差数据和激光干涉仪测量的误差分别代入机床综合误差预测模型进行对比验证。从对比结果中可以看出，利用两种方法建立的机床综合误差模型差别在3.0μm，可以满足机床误差补偿的要求。

关键词：球杆仪;几何误差辨识;综合误差预测模型;比对结果

中图分类号： TG806  文献标志码：A

文章编号：1672-1098（2021）01-0018-06

收稿日期：2020-07-13

基金项目：国家自然科学基金资助项目（51675004）;安徽高校自然科学研究基金资助项目（KJ2019A0844）

作者简介：杨洪涛（1972-），男，福建莆田人，教授，博士，研究方向：精密测试技术、仪器精度理论及应用。

A Geometric Error Identification and Modeling  of CNC Machine Tool Based on Double Ball-bar

YANG Hongtao1，2，ZHANG Yu1，2，LI Li1，2，MA Qun1，2，WANG Jun3

（1. School of Mechanical Engineering， Anhui University of Science and Technology ， Huainan Anhui  232001， China;2. Anhui Key Laboratory of Mine Intelligent Equipment and Technology， Anhui University of Science and Technology， Huainan Anhui  232001， China;3. School of Advanced Manufacturing Engineering， Hefei University， Hefei Anhui  230001， China）

Abstract：To solve the problems of the complicated operation process and the low efficiency of geometric error identification and modeling of computer numerical control （CNC） machine tools with the existing laser interferometers， a new method of geometric error identification and modeling was proposed for CNC machine tools based on double ball-bar. The identification model was established of the relationship between the double ball-bar reading and the corresponding geometric error in each plane of the machine tool with the three-plane arc trajectory measurement method and the double ball-bar utilized to measure the error， realizing the geometric error Identification and the establishment of a comprehensive error prediction model of the machine tool and a comparison experimental device  with the laser interferometer used to measure the actual geometric error of the machine tool. The geometric error data identified by the double ball-bar and the error measured by the laser interferometer were respectively substituted into the comprehensive error prediction model of the machine tool for comparison and verification. From the results， it is found that the difference between the two is 3.0 μm， which meets the requirements of the machine tool error compensation.

Key words：double ball-bar; geometric error identification; comprehensive error prediction model; comparison results

数控机床在机测量系统是由机床本体和触发测头组成，通过测头产生触发信号，触发机床本身的三维坐标读数装置进行读数，实现被测点的三维坐标测量。如果不提高测量系统精度，直接利用机床与测头相结合开展测量，不满足测量系统精度必须三倍高于被测零件精度的要求，因此必须利用误差分离方法对机床各项几何误差进行测量，建立高精度综合误差预测模型进行测量误差补偿[1]。目前数控机床几何误差辨识方法主要采用双频激光干涉仪、球杆仪、平面光栅等设备[2]。利用激光干涉仪每测量1个误差都需更换光学镜组且光路不易调整，效率低，光学组件价格昂贵[3]。球杆仪主要通过测量常规的三平面圆弧轨迹便可分离与辨识包括滚转角误差在内的21项几何误差[4-5]，但存在辨识精度问题。近年来，国内外学者提出了很多基于球杆仪辨识空间误差方法，主要针对机床旋转轴的误差辨识[6-9]，而对直线轴误差辨识研究缺乏完善的实验结果对比验证[10]。对于机床综合误差建模，大部分采用激光干涉仪测量各单项误差，进而利用微分法、多体系统理论等方法建立综合误差预测模型[11-13]，但利用球杆仪测量辨识的几何误差建立机床综合误差建模研究较少[14]。为了提高基于球杆仪的机床几何误差辨识精度和综合误差建模精度，本文采用球杆仪的三平面圆弧轨迹法，建立了球杆仪读数与数控机床各平面内几何误差项之间的模型，辨识出各项几何误差值，进而利用辨识数据建立机床综合误差预测模型，并开展对比验证实验。

1  球杆仪数控机床几何误差辨识方法

1.1 数控机床几何误差源

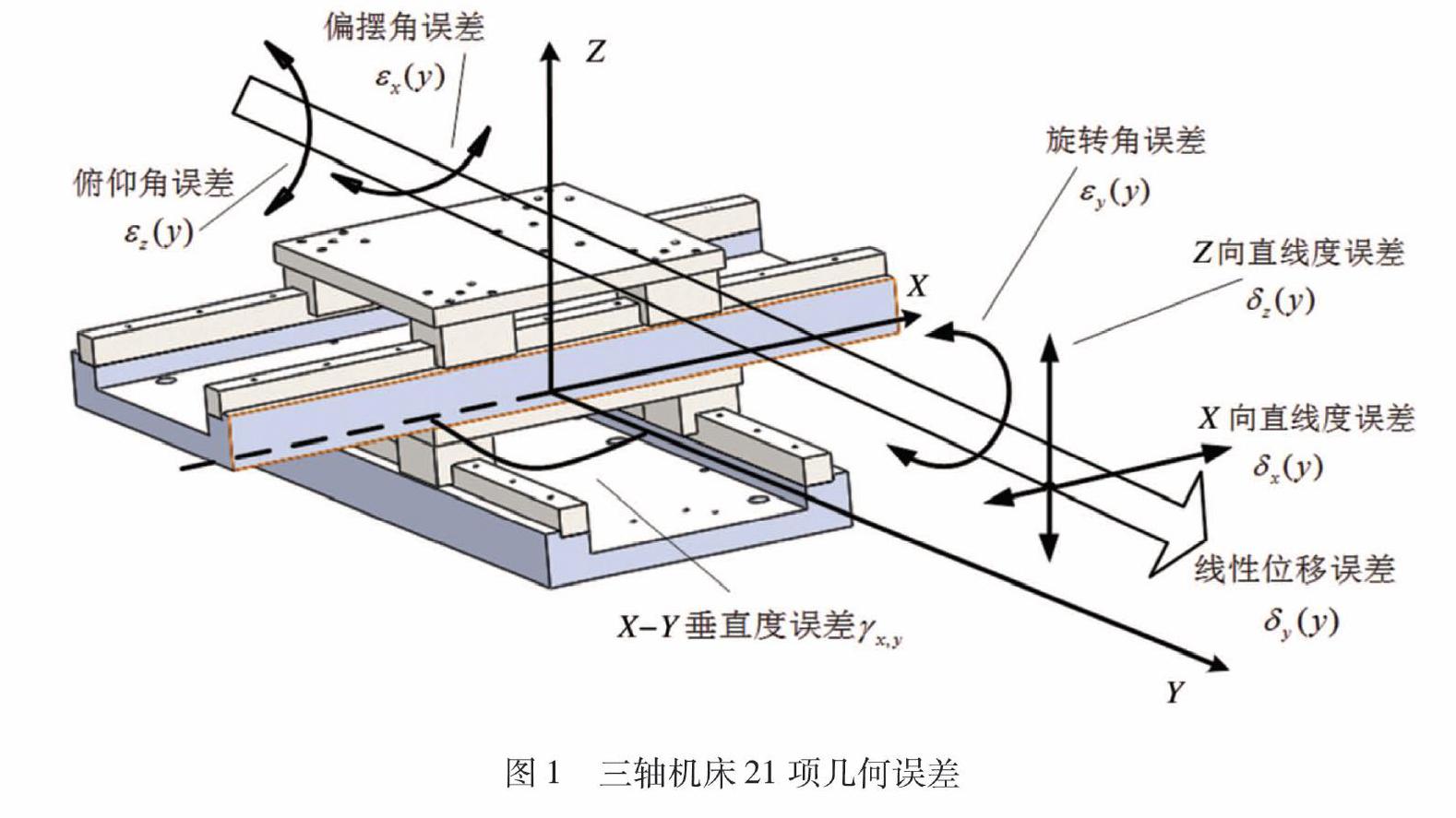
本文以XYTZ型立式加工中心为研究对象，如图1所示，三轴数控机床的机床部件沿着Y轴运动时，共有6项几何误差，三轴共产生18项位置相关几何误差，加上3个垂直轴之间的3项垂直度误差，共有21项几何误差，如表1所示。

1.2 球杆仪的工作原理

本文采用三平面圆弧轨迹测量法和球杆仪对误差进行测量[15]，球杆仪的测量原理示意图如图2所示。令工作台安装基座上吸附的精密球中心坐标为O（0，0，0），在主轴安装基杆上吸附的精密球中心坐标为P（x，y，z），当工作台进行理论圆插补运动时，吸附在主轴上的精密球中心坐标由于机床几何误差影响变为P′（x′，y′，z′），设 Δx，Δy和Δz分别是P点与P′点之间误差在X、Y、Z方向上的分量。

由于几何误差的存在，球杆仪的实际长度可以表示为

（r+Δr）2=（x+Δx）2+（y+Δy）2+（z+Δz）2 （1）

式中：Δx，Δy，Δz都在微米级，忽略其二次项，可得球杆仪实际长度变化可以计算如下

Δr=1r（Δx×x+Δy×y+Δz×z）（2）

式中：Δr是球杆仪读数，即球杆长变化量。该式即为球杆仪测量数控机床几何误差的理论基础，由此可以推导出数控机床的误差分离模型。

三平面圆弧轨迹测量法即在数控机床三正交平面进行，如图3所示，球杆仪在XY平面上进行检测时，机床主轴Z方向停止运动。将球杆仪水平安装，球杆仪以工作台侧支座上支承的精密球中心为回转中心，按照数控指令完成半径为r的圆弧插补进给，顺时针和逆时针各1次，同理，在YZ平面和ZX平面上的进行检测时，主轴X和Y方向停止运动。其中，在XY平面进行360°（越程45°）圆弧测量，在ZX平面、YZ平面分别进行220°（越程2°）圆弧测量[16]。此时球杆长度变化量Δr即为该平面内综合误差，再将球杆仪的检测数据代入几何误差辨识方法建立的球杆仪读数与机床各平面内对应几何误差之间的辨识模型，实现几何误差辨识。

1.3 几何误差辨识方法

利用4×4齐次坐标变换矩阵HTM（Homogeneous Transformation Matrix），对数控机床几何误差分量进行辨识。

Y轴的HTM可以写成

Trans（y）=1000010ym00100001（3）

忽略高階项，Y轴几何误差的HTM可以写成

E（y）=1-εz（y）εy（y）δx（y）εz（y）1-εx（y）δy（y）-εy（y）εx（y）1δz（y）0001（4）

根据式（3）和（4）可得到床身R到Y轴坐标系的包含各几何误差的HTM

RTT=Trans（y）×E（y）=    1-εz（y）εy（y）δx（y）εz（y）1-εx（y）δy（y）+ym-εy（y）εx（y）1δz（y）0001（5）

使用相同的方法，可以分别建立Y轴和X轴，X轴和工件W，Z轴RZT，主轴S和Z轴，刀具T与主轴S之间的HTM，同理，刀具T相对于机床床身R的HTM可以如下表示，它们用于建立机床的整个运动学模型。

RwT=RYT·YXT·XwT·TW（6）

RTT=RZT·ZST·STT·Tt （7）

式中：TW工件理论加工点在工件坐标系中的位置坐标矢量，Tt为刀具坐标系T中机床刀具尖端的位置坐标矢量。

根据式（6）和式（7）可得这两个矩阵的差值即为工件和刀尖之间的相对位移误差矩阵，即机床的几何误差矩阵如式（8）所示。

WTT=RTT-RWT（8）

在其求解过程中，舍去误差二次项及高次项，得到简化的数控机床沿X、Y、Z坐标轴运动的几何误差模型，并分别代入式（2）中，再经过一系列简化计算，得到1个有12个系数的方程，如式（9）所示，这些系数与球杆仪长度的偏差Δr有关。

Δr=1rxdxz（zr）2-z·γx，z+2d·dxz（zr2）-Xw+YW2dyx（xr2）+2dxy（yr2）-ZW2dzx（xr2）+eyy（yr）-x-dxx（xr）-dxy（yr）2+ydyz（zr）2-z·γy，z-2d·dyz（zr2）-XW2dxy（yr2）+2dyx（xr2）-YW+ZWexx（xr）+2dzy（yr2）-2x·dxy（yr2）-dyx（xr）2+x·γx，y-y-dyy（yr）+zz+dzz（zr）+d+XWeyy（yr）+2dzx（xr2）-YW2dzy（yr2）+exx（xr）-ZW+x·eyy（yr）-dzx（xr）2-dzy（yr）2（9）

式中：dxx，dyy，dzz，dyx，dzx，dzy，dxy，dxz，dyz，exx，eyy，ezz为未知数; γx，z，γy，z，γx，y为三个垂直度误差，由球杆仪测量得出;x，y，z，Δr分别为各测量点的理论坐标值和径向误差值;r为测量半径。只要求出这些系数，即可计算不同位置的各项几何误差值。

2 数控机床综合误差预测模型

根据齐次坐标变换原理建立的综合误差模型[17]，考虑到3个轴的滚转角误差数值非常小且对数控机床在机测量系统的总体误差影响较微小，所以忽略滚转角误差的影响，则可简化模型为

Δx=-δx（x）-δx（y）+δx（z）-yεz（x）-zεy（x）-  zγx，z+yγx，yΔy=-δy（x）-δy（y）+δy（z）+zεx（y）-zγy，zΔz=-δz（x）-δz（y）+δz（z）（10）

式中：δx（x）为X轴定位误差，δy（x），δz（x）分别为X轴运动时Y和Z向的直线度误差，εz（x），εy（x）分别为X轴的偏摆角和俯仰角误差;γx，y、γy，z、γx，z分别为X轴和Y轴之间、Y轴和Z轴之间、X轴和Z轴之间的垂直度误差。

根据式（10）建立数控机床综合误差预测模型

E（x，y，z）=Δx2+Δy2+Δz2（11）

3 对比验证实验

以沈阳机床VMC850E三轴立式加工中心为数据采集对象，分别采用雷尼绍公司的QW20球杆仪和激光干涉仪XL-80对同1台机床进行测量。该机床XYZ三轴行程分别为800mm、500mm、540mm，试验中使用的球杆仪和激光干涉仪分别具有0.1μm 和1nm的分辨率，实验装置组成如图4所示。

3.1 实验方案设计

QW20球杆仪的分辨率为0.1μm，杆的长度取100mm，即测量空间范围为200mm×200mm×200mm，用球杆仪三平面圆弧轨迹法分别测量机床在XY平面、YZ平面、ZX平面的综合几何误差。将QW20球杆仪安装在工作台上并在机床空载状态下进行测量，使机床主轴以480mm/min的速度在各平面内作半径为100mm的圆弧轨迹插补运动，顺时针和逆时针各1次，每个平面共进行3次测量，其平均值作为球杆仪检测的最终值，以减少随机误差。如图4（a）所示为球杆仪现场检测图。以XY平面机床顺时针运行为例，QW20球杆仪每旋转10°选取1次数据，如表2所示为不同位置的球杆仪测量数据。

以机床各单项几何误差为例进行模型验证，利用激光干涉仪在球杆仪相同检测位置进行各单项误差检测，间隔5mm采集1次数据，每个测点均单向测量3次。如图4（b）所示为激光干涉仪现场检测图。

3.2 几何误差辨识与建模效果验证

为验证上述几何误差辨识结果的正确性，以机床X轴定位误差和X轴Z向直线度误差为例，将利用球杆仪辨识出的几何误差数据和激光干涉仪测量出机床的实际几何误差进行比较，结果如图5所示。图中两条曲线表示利用该方法辨识结果计算得到的误差值，两组离散点表示激光干涉仪测量值的均值。激光干涉仪测量各直线轴滚珠丝杠的几何误差，且测量精度高，图5中，由于机床本身存在的缺陷，激光干涉仪测得X定位误差不连续，有很大的跳跃和下降，而球杆仪辨识方法无法对机床本身存在的缺陷进行预测，呈光滑的曲线。因此图中激光干涉仪得到的结果比球杆仪辨识方法得到的结果波动更大。

从图5中可以看出，通过球杆仪辨识得到的几何误差值与激光干涉仪检测出的相应几何误差值的变化趋势基本一致，除去粗大误差外，两者间的偏差均在2.7μm以下，平均偏差仅为1.5μm，从而验证了该数控机床几何误差辨识的正确性。

为了进一步验证该数控机床几何误差辨识的效果，分别将利用球杆仪辨识出的几何误差数据和激光干涉仪测量的误差代入机床综合误差预测模型进行对比验证。将两者数据分别代入式（11）中，得到各自数控机床综合误差预测值E（x，y，z），为了方便观察，取测量空间范围200mm×200mm×200mm正方体对角线上点空间坐标（x，y，z）的预测数据，其中x=y=z=i，0≤i≤200，同时剔除对角线上由于机床本身存在的缺陷而造成粗大误差外的部分数据，其预测误差结果比较如图6所示。

从图6中可以看出，两者预测结果的变化趋势基本一致，两者间的偏差均在3.0μm以下，平均偏差仅为1.5μm，从而验证了该数控机床几何误差辨识与建模方法的正确性。

5 结论

（1）针对数控机床利用齐次坐标变换矩阵分析位置相关几何误差模型，建立了待辨识误差系数与球杆仪测得的径向误差值之間的辨识方程组。进行了基于球杆仪的数控机床几何误差辨识与建模。

（2）利用球杆仪辨识出的几何误差代入建立的综合误差预测模型，与激光干涉仪的综合误差建模的结果进行对比，结果表明该数控机床几何误差辨识与建模方法具有较高的准确性，最大辨识误差为3.0μm，且成本低，耗时短，操作简便。

参考文献：

[1] 董泽园， 李杰， 刘辛军， 等. 数控机床两种几何误差建模方法有效性试验研究[J]. 机械工程学报， 2019，55（5）：137-147.

[2] 王金栋， 郭俊杰， 费致根， 等. 基于激光跟踪仪的数控机床几何误差辨识方法[J]. 机械工程学报， 2011，47（14）：17-23.

[3] 杨婧， 冯其波. 数控机床空间几何误差测量研究进展[J]. 仪器仪表学报， 2017，38（8）：1 901-1 911.

[4] 陈光胜， 李郝林. 多轴数控机床转台误差快速检测与分离[J]. 仪器仪表学报，2013， 34（11）：2 499-2 505.

[5] 李欢玲. 基于多体理论的数控机床几何误差补偿技术的研究[D]. 南京：南京航空航天大学， 2009.

[6]  CHEN J X，LIN S W，ZHOU X L，et al. A ballbar test for measurement and identification the comprehensive error of tilt table[J]. International Journal of Machine Tools and Manufacture， 2016 （103）：1-12.

[7] 冯刚， 付国强， 孙磊， 等. 多轴数控机床转台几何误差辨识新方法[J]. 浙江大学学报（工学版）， 2015， 49（11）：2 083-2 091.

[8] 田文杰， 郭龙真， 刘海涛. 数控机床几何误差源的快速辨识方法[J]. 天津大学学报（自然科学与工程技术版）， 2016，49（2）：171-177.

[9] 徐凯， 李国龙， 何坤， 等. 基于球杆仪的直线轴位置相关误差辨识研究[J]. 仪器仪表学报， 2019，40（5）：1-9.

[10] 耿金华. 数控机床切削力误差建模及三维热变形临界点分析与应用[D]. 淮南：安徽理工大学， 2015.

[11] CHEN J X ， LIN S W ， ZHOU X L ， et al. A comprehensive error analysis method for the geometric error of multi -axis machine tool[J]. International Journal of Machine Tools & Manufacture， 2016（103）：56-66.

[12] 杨泽青， 李增强， 刘奇， 等. 立式加工中心综合误差建模及实验分析[J]. 现代制造工程，2019（10）：6-13.

[13] 赵帼娟，张雷，卢磊，等.四轴抛光平台综合误差建模及分析[J].吉林大学学报，2014，44（6）：1 676-1 683.

[14] 杨洪涛， 庞勇军， 李莉，等. 数控机床XY工作台动态定位误差分析与建模[J]. 组合机床与自动化加工技术， 2019（2）：41-44.

[15] YANG SEUNG-HAN，LEE HOON-HEE，LEE KWANG-IL.Faceand Body-Diagonal Length Tests using a Double Ball-Bar for Squareness Errors of Machine Tools[J].International Journal of Precision Engineering & Manufacturing，2018，19（7）：1 039-1 045.

[16] ZHONG L，BI QI，WANG Y.Volumetric accuracy evaluation for five-axis machine tools by modeling spherical deviation based on double ball-bar kinematic test[J].International Journal of Machine Tools and Manufacture，2017 （122）：106-119.

[17] 楊建国， 范开国， 杜正春. 数控机床误差实时补偿技术[M]. 北京： 机械工业出版社， 2013：62.

（责任编辑：李 丽）