基于改进滑模变结构的加筋板振动控制研究
马天兵 丁威海 周青 杜菲


摘 要:针对外部持续激励下加筋板振动滑模变结构控制系统进入稳态的时间较长,且存在抖振现象的问题,在传统幂次、指数趋近律的基础上,构建新的自适应因子,形成了一种改进趋近律滑模变结构控制算法,并证明其收敛性。分析3种不同趋近律对系统振动控制的效果,仿真和实验结果表明,改进后的方法取得了比传统滑模变结构算法更优的控制效果,能在一定程度上削弱抖振。
关键词:加筋板;滑模变结构控制;改进趋近律;振动
中图分类号: TP273.5 文献标志码:A
文章编号:1672-1098(2021)01-0007-06
收稿日期:2020-05-20
基金项目:安徽高校自然科学研究基金资助项目(KJ2020A0281);安徽省博士后基金资助项目(2017B172);安徽高校协同创新基金资助项目(GXXT-2019-048);安徽省自然科学基金资助项目(2008085ME178);安徽高校学科(专业)拔尖人才学术资助项目(gxbjZD2020063)
作者简介:马天兵(1981-),男,安徽庐江人,教授,博士,硕士生导师,研究方向:压电能量回收、振动主动控制方面研究。
Research on Vibration Control of Stiffened Plate Based on Improved Sliding Mode Variable Structure
MA Tianbing, DING Weihai, ZHOU Qing, DU Fei
(School of Mechanical Engineering, Anhui University of Science and Technology, Huainan Anhui 232001, China)
Abstract:To the problem that the sliding mode variable structure control system of the stiffened plate vibration with external continuous excitation takes a long time to enter the steady state and the chattering phenomenon is relatively obvious, a new adaptive factor is constructed on the basis of the traditional power and exponential approach law forming an improved sliding mode variable structure control algorithm of the approach law, and its convergence is proved. The results of simulation and experiment show that the improved method has better control effect than the traditional algorithm and will weaken chattering to a certain extent.
Key words:stiffened plate; sliding mode variable structure control; improved approach law; vibration
隨着工业领域对于材料各项性能要求的提高,高强度、强耐用性的加筋板结构的应用也愈发广泛。但是当加筋板结构受到外力扰动时,会产生振动,并带来一系列不利影响,因此对其振动的控制十分必要[1-3]。加筋板控制系统中常采用反馈控制、线性二次高斯(LQR)、鲁棒控制等方法,其中,滑模变结构控制广受国内外研究学者的青睐[4-6]。
滑模变结构控制算法属于非线性控制算法范畴,此控制策略与其他方法不同之处在于系统是动态变化的,控制过程中无需系统在线识别,并且不受系统参数的影响,这就使得滑模变结构控制具有一定的抗干扰能力,具备鲁棒性[7-9]。文献[10]利用自适应滑模变结构控制方法,解决航天器姿态控制系统中的强非线性位姿控制问题,并且消除了外界不确定扰动力对于航天器飞行姿势形态的干扰。该方法很好地凸显了滑模变控制算法具有的较优的抗扰动效果。文献[11]对PWM整流器模型预测控制稳态波纹大、采样频率高、开关频率不固定等问题,结合了滑模控制,研究了一种新的种改进的模型预测控制方法。相对于传统的模型预测控制,改进后的方法能够显著地减小功率脉动,增强系统的动态性能和稳态特性,取得了不错的效果。文献[12]在研究磁悬浮轴承转子系统时,结合该系统的强非线性特征,提出一种Terminal滑模变结构控制算法,并设计了4输入4输出的控制策略,使得磁悬浮轴承转子系统有了更高效的控制。此方法与传统的PID控制器的控制结果相比,具有很好的抗干扰能力,并且在很短的响应时间内减弱抖振现象。文献[13]对于汽车制动过程中防抱死制动系统具有的非线性、时变性和不确定性的问题,设计了以最佳滑移率为目标的滑模变结构控制器,并且采用径向基神经网络实时调整滑模变结构控制器参数,削弱了滑模变结构控制中的抖振现象,并能使车辆具有良好的制动效果。尽管滑模变结构控制具有很好的抗扰动能力,但控制抖振现象在滑模变结构控制中一直存在,但抖振的产生与控制的抗扰动能力是相关的,需要权衡两者以达到较好的稳态。
针对滑模变结构控制中的抖振问题,文献[14]在滑模算法控制电机的基础上加入了模糊切换增益控制,不但没有影响滑模控制响应速度快的优点,并且相对于单纯的滑模控制电机,加入模糊切换增益算法,有效的减少了电机跟踪正弦曲线的抖动。文献[15]利用神经网络与滑模变结构相结合的复合控制方法来解决这一问题,并在伺服系统的时变性问题上得到了应用。但大部分学者通过研究如何改进滑模变结构中的趋近律,来减弱抖振现象。文献[16]在研究永磁同步电机的转矩波动问题时,设计一种新型滑模趋近律,对比电机在传统指数趋近律下的转矩抖动,该方法使抖动得到了很大的改善。并且该新型趋近律下的控制系统具有抖动小,自适应性强等优点。文献[17]提出一种将分数阶PI与变速趋近律相结合的改进型PI趋近律,基于该改进趋近律下的滑模控制算法减弱了系统输出的抖振问题,并且鲁棒性强。综上,研究学者们在看中滑模变结构控制具有抗干扰优势的同时,通过对趋近律进行改进来获取抖振小、鲁棒性强的控制系统成了振动研究的热门与趋势。
针对滑模控制系统抖振等问题,本文选择压电加筋板作为研究对象,对传统趋近律进行改进,并证明其收敛性,为验证改进趋近律控制效果,搭建加筋板仿真控制系统和实验平台,仿真与实验验证改进算法的控制有效性和优越性。
1 滑模变结构原理及收敛性证明
抖振问题是滑模变结构控制中一直存在的问题,也是历来人们研究的重点,其特点在于它可以削弱但不可消除,如果消除了抖振,也就消除了变结构控制对外界抗扰动的能力,从而失去鲁棒性。为了削弱控制的抖振问题,同时又要在有限时间内到达切换面,并且快速趋近滑动模态,那么,可以从趋近律方面入手,进而改善运动轨迹的动态品质。目前较为常见的有
(1)指数趋近律
s·=-ε sgns-ks ε>0,k>0(1)
式中:s为超曲面,k是趋近律,ks为指数趋近项,sgn为符号函数,ε为速度。
其中,ks为指数趋近项,当s较大时,即运动点离切换面较远,系统能快速趨近切换面,并且指数趋近律还能使运动点在即将到达切换面时速度较小。同时为了保证有限时间内抵达切换面,满足切换面上存在滑动模态的条件,式中等速趋近项 的作用就是使运动点接近切换面时,速度是 而不是0,保证有限时间内趋近。
(2)幂次趋近律
s·=-k|s|αsgns k>0,α>0(2)
式中:α为常数。
同样为了较快进入滑动模态,幂次趋近律可以调整 值大小,使运动点离滑动模态较远时以较快的速度向它靠近,靠近滑动模态(s较小)时,则保持较小的控制增益,可以降低抖振。
结合考虑传统幂次、指数趋近律的优缺点对趋近律进行改进,改进趋近律如下
s·=-k0|s|sgn s-ks k0>0,k>0(3)
改进的趋近律可以看成在指数趋近律的基础上把速度项改成k0|s|,使系统接近切换面即s越小时,趋近速度越小,减少抖振;也可以看成对幂次趋近律增加了一个指数项-ks,使运动点离切换面较远时以一个较快的速度趋近切换面,保证快速趋近,这样就满足了快速趋近和较少抖振的需求。
“滑模”区域上的点都是终止点,运动的点在该区域运动将会被“吸引”在该区域,该区域附近的点都将满足
lims→0ss·≤0(4)
为了说明改进趋近律的运动点也具有这一特性,需要对其进行验证。首先,根据实际被控对象压电加筋板模型
x··=-f(x,t)+bu(t)+d(t)(5)
式中:x代表结构振动位移,f(x,t)是加筋板振动函数,b为常数,u(t)为控制输出电压,d(t)为外界干扰。
以及跟踪误差:e(t)=xd(t)-x(t),其中,xd(t)和x(t)分别是参考模型的位移以及加筋板的实际位移。
对其进行滑模函数设计为
s(t)=ce(t)+e·(t)(6)
式中:c>0。
对式(6)进行求导,可以得到如下
s·(t)=ce·(t)+e··(t)=c(x·d(t)-x·(t))+(x··d(t)-x··(t))=c(x·d(t)-x·(t))+(x··
d(t)+f(x,t)-bu(t))-d(t))(7)
由式(3)和式(7)可以得到等式
c(x·d(t)-x·(t))+(x··d(t)+f(x,t)-bu(t))-d(t))=-k0|s|sgn s-ks(8)
将上式化简,则可以得到
u(t)=1b(k0|s|sgn s+ks+c(x·d(t)-x·(t))+x··d(t)+f(x,t)-d(t))(9)
对于干扰d(t),由于是未知,我们可以利用干扰界来进行设计。将d(t)取为dc,其中dc为跟干扰界相关的正实数。则
u(t)=1b(k0|s|sgn s+ks+c(x·d(t)-x·(t))+x··d(t)+f(x,t)-dc)(10)
将式(12)代入式(8)中并化简得到
s·=-k0|s|sgn s-ks+dc-d(t)(11)
假使对于d(t)干扰的上下界为dL和dU,则
dL≤d(t)≤dU(12)
那么对于实数dc的选取,如下
当s(t)>0时,s·=-k0s-ks+dc-d(t),为了使ss·≤0,则取dc=dL。
当s(t)<0时,s·=-k0s-ks+dc-d(t),为了使ss·≤0,则取dc=dU。
因此,对dc进行设计如下
dc=dU+dL2-dU-dL2sgn s(13)
即能保证在dc可取的范围内,改进趋近律后的滑模运动满足lims→0ss·≤0的收敛条件。
2 改进滑模变结构仿真控制
2.1 加筋板模态参数识别
搭建加筋板实物作为后续控制研究对象,具体为尺寸为400mm×600mm×1.2mm的壁板。主要控制的是加筋板的第一阶模态振动。实验中的扫频信号采用60~300Hz的正弦信号对加筋板进行扫频激励,利用实验模态分析方法获取的一阶模态振动频率为f1=213.4Hz,运用半功率带宽阻尼分析法得第一阶阻尼比为ξ=-0.012 9,通过实验测得δM-1=0.1m,其中δ为力因子,M为一阶模态下的模态质量。
综合上述结果可得一阶模态的空间状态方程为
X·=01-1 801 201.2-34.6X+00.1uY=01X (14)
2.2 仿真结果及分析
在MATLAB里编写指数趋近律、幂次趋近律和改进趋近律3种滑模控制器程序, 为保证对比有效性, 其中共同参数选择相同值, 令k=100、c=50、 k0=1 000、 b=0.07; 而不同算法内的独属参数则选择效果最佳参数,多次实验下发现取值ε=2、α=1.5时效果最佳。
分别对不同趋近律控制器下的系统进行仿真控制,激励信号设置相同,系统中积分初始值均取0,仿真时间为0.5s,经过仿真控制系统运行,3种不同控制算法下控制前及控制后的振动位移对比结果如图1~图3所示。
根据图1~图3仿真控制结果可知,三种控制均达到了振动控制的效果,但控制效果的好坏存在差异。3种控制方法在未控制前的振动位移均稳定在2.11×10-5m左右,在分别基于指数趋近律、幂次趋近律以及改进趋近律的3种滑模控制器下,振动位移分别被控制至6.70×10-6m、7.52×10-6m、4.95×10-6m,可以看出,基于改进趋近律控制下的控制结果振动位移最低,振动控制效果最佳。根据振动控制波形结果可知,改进趋近律的滑模控制可使被控振动信号更快进入稳定状态,根据图4可知,相对于指数趋近律和幂次趋近律,采用改进趋近律控制后的抖振现象不显著,说明该方法对抖振实现了较好的抑制作用。仿真效果综合来看,基于改進趋近律的滑模控制器能够很好地实现振动控制,并且具有一定的优越性。
3 改进滑模变结构振动控制实验
3.1 实验平台搭建
本压电加筋板振动主动控制实验是在CompactRIO(CRIO)平台下的振动控制实验,所用压电传感片和压电作动片的尺寸规格是50mm×50mm×0.2mm,粘贴于加筋板一阶模态振动最大处前后对称位置。由信号发生器输出正弦激励信号,激励信号的频率设置为加筋板一阶模态频率213Hz,经过功率放大器放大后,通过激振器作用于加筋板上,CRIO的信号采集模块采集压电传感片振动响应信号,经过CRIO实时分析运算后由输出卡输出控制制加筋板振动,实验平台如图5所示。
3.2 实验结果与分析
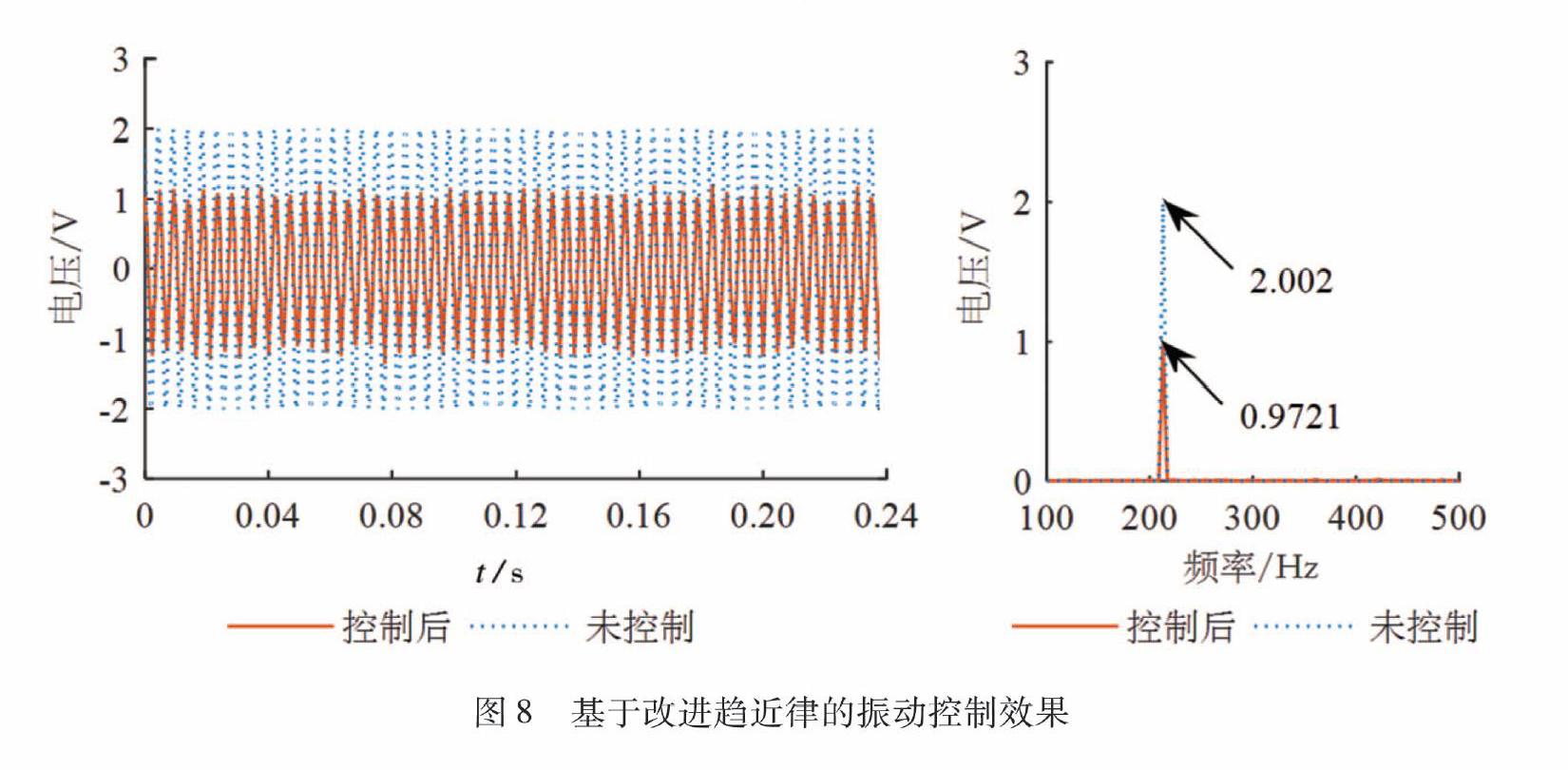
在信号发生器中设置正弦激励信号,频率为213Hz,通道采样率设置为10k,根据模态分析中的内容,加筋板参数取上文求取的模态参数。控制器参数按照仿真中选取的参数设定。实验时首先运行控制程序,待程序运行起来并且前面板中出现信号波形图,然后打开信号发生器,设定好激励信号后选择输出,驱动激振器进行激励,然后逐步缓慢调节功率放大器,调节输出控制信号的放大倍数直至运行稳定,并确保每种趋近律下的未控制前的电压幅值一致,经多次实验得到不同趋近律下的振动控制结果如图5~图7所示。为更好的说明控制效果,频谱选择包含213Hz振动频率的100~500Hz频段结果进行显示,由于频率分辨率的影响,该频段主要振动频率较为显著。
根据图6~图8实验的时频域结果可知,基于改进趋近律的滑模变振动控制算法实现了振动控制,由未控制的2.002V下降至了0.972 1V,降低了51.4%,相较于指数趋近律30.7%以及幂次趋近律的36.4%的控制效果,明显较优。相对于指数趋近律以及幂次趋近律,基于改进趋近律抖振的高频振荡也得到了一定程度的削弱。
4 总结
本文综合考虑传统幂次、指数趋近律的优缺点,并在传统趋近律的基础上作了改进,得到新的改进趋近律,推导出基于改进趋近律的滑模控制器函数,并验证了其稳定性。在Simulink中设计振动控制仿真实验系统,仿真结果表明,相对传统指数趋近律和幂次趋近律滑模控制,改进趋近律的控制效果较佳,振动控制进入稳态较快,振动抑制效果也有所改进。此外,设计并搭建压电加筋板振动实验平台进行振动控制,实验结果同样表明,基于改进趋近律的滑模控制器控制效果可达到51.4%,能够较好地实现振动控制,能在一定程度上削弱抖振,并且相较于传统趋近律控制也具有明显的优越性。
参考文献:
[1] 张文春, 段树林, 赵连行. 线激励下船舶混合构型加筋板的振动特性[J]. 船舶力学, 2016, 20(7): 858-865.
[2] 李凯, 何书韬, 邱永康, 等. 附加多个集中质量加筋板的自由振动分析[J]. 中国舰船研究,2015,10(5):66-70.
[3] 尹剑飞, 温激鸿, 肖勇, 等. 基于高级统计能量分析的周期加筋板振动特性研究[J]. 物理学报, 2015,64(13): 190-199.
[4] BAILEY T,HUBBARD J E.Distributed Piezoelectric-Polymer Active Vibration Control of a Cantilever Beam[J]. Journal of Guidance Control and Dynamics, 1985, 5(8): 605-611.
[5] 赵芝梅, 盛美萍, 杨阳. 多点激励下加筋板壳耦合结构的振动特性[J]. 工程力学,2013, 30(11): 239-244.
[6] 帅仁忠, 朱雷威. 基于模态应变能加筋板敷设阻尼性能优化[J]. 现代商贸工业, 2017(8): 191-192.
[7] 张海刚, 胡添添, 王步来, 等. 一种改进的PMSM滑模变结构控制策略研究[J]. 电气传动, 2019, 49(10):13-15.
[8] ZHIQIANG LI,LIQING CHEN,QUAN ZHENG,et al. Control of a path following caterpillar robot based on a sliding mode variable structure algorithm[J]. Biosystems Engineering,2019,186:293-306.
[9] 于涛, 赵伟, 杨昆. 一类欠驱动系统的滑模变结构控制[J]. 控制工程, 2019, 26(10): 1 824-1 829.
[10] 王永俊, 贾建芳. 航天器自适应滑模变结构姿态控制[J]. 电子测量与仪器学报,2019, 33(9): 9-15.
[11] 孙鹤旭,郝正赫,董砚,等.定频模型预测控制与滑模控制相结合的PWM整流控制策略[J].微特电机,2020,48(7):47-51.
[12] 张东波, 方玺, 张小玉, 等. 主动磁悬浮轴承的Terminal滑模变结构控制[J]. 武汉大学学报(工学版), 2019, 52(8): 736-740.
[13] 夏志成,邹广德,董威.基于RBF神经网络的ABS滑模变结构控制研究[J].山东理工大学学报(自然科学版),2020,34(3):44-48.
[14] 刘牮,杨鹏,马文良,等.基于模糊切换增益调节的PMSM滑膜控制算法的仿真[J].电子测量技术,2019,42(19):106-110.
[15] 何禹锟, 高强, 侯远龙, 等. 定深电液伺服系统的复合滑模控制研究[J].电光与控制, 2019, 26 (10): 78-82.
[16] 宗学军, 朱庆雪, 张居华. 基于快速趋近律的永磁同步电机滑模控制[J]. 微特电机, 2019, 47(10): 63-66.
[17] 郭伟, 朱承平, 李涛, 等. 基于改进型PI趋近律的无刷直流电机滑模控制[J]. 测控技术,2019, 38(9):122-125.
(责任编辑:李 丽)

