运动平台混响背景下基于低秩稀疏分解的目标回波增强

王 燕 贺玉梁 邱龙皓 邹 男

(哈尔滨工程大学水声技术重点实验室 哈尔滨 150001)

(哈尔滨工程大学水声工程学院 哈尔滨 150001)

1 引言

随着科学技术的不断发展，水下无人航行器(UUV)因其使用灵活度大和可连续工作等优点而备受关注。由于潜艇声隐身技术的发展，目标辐射噪声越来越低，主动声呐逐渐成为水下安静目标探测的重要手段之一。主动声呐通常产生目标方位随距离(或时间)变化的滤波结果，也被称为方位历程图，尽管在滤波中可能已经考虑了很多混响抑制策略，但在混响影响严重的近距离区域，输出仍可能受到严重的干扰，尤其在浅海环境下，某些时候甚至无法有效地判决并识别真实目标[1]。

显然，混响的进一步抑制和目标回波的增强，需要利用二者在某些特征上的差异性。对近程目标的方位历程图而言，由于散射环境是慢变的，混响干扰背景相邻帧间具有一定的潜在相干结构，因而可以认为混响成分位于低秩的混响子空间；由于主动平台的运动，目标回波在逐帧间具有不同的空间位置，此外它们通常是稀疏的，且相对混响成分的能量而言是较弱的。在上述的一般假设下，可将近程目标方位历程图检测输出表示为低秩的混响、稀疏的运动目标回波和噪声成分之和。至此，面临的问题转变为3种成分的分离问题，或者称为矩阵的低秩稀疏重构(复原或分解)问题。

实现上述分解可有两类方法：高计算复杂度的离线算法和低计算复杂度的在线算法。离线算法中，最直接的方法来自主成分分析(PCA)思想[2,3]，其假定在待分离数据的奇异值分解中，最大的少数几个奇异值对应的左特征向量展成的特征子空间近似为混响主成分的子空间，中等大小的奇异值对应较弱的目标回波成分，最小的奇异值对应噪声成分。但其实现良好分解的隐含前提假设是，稀疏目标回波对应的特征空间与混响主成分的特征空间是正交的，因而二者仅通过奇异值的幅度就是可区分的，但在复杂的数据模型下，这并不是总能得到满足。另外，整个混响成分通常不是严格低秩的，在主导的成分之外还存在着相对较弱的成分，这些较弱的混响成分通常不是该方法能够分离的。为了应对这些更复杂的情形，这里考虑PCA方法的一个推广，即图像处理领域广泛研究的稳健主成分分析(Robust PCA, RPCA)方法[4–6]，将其应用于本文的离线低秩稀疏分解问题中。与离线问题模型相比，在线模型的问题规模更小，问题的求解具有实时性，且具有一定的跟踪混响子空间的能力。基于主成分分析的在线化思想，解决问题的关键在于如何有效快速地更新混响子空间估计[7–9]。文献[9]在正交迭代变体形式基础上，利用Householder镜像变换，实现了子空间的在线跟踪快速算法(FDPM)，具有较快的跟踪和收敛速率。本文在该算法基础上，进一步设计推导了解决向量在线低秩稀疏分解问题的方法。

2 低秩稀疏表示模型

考虑将近程目标方位历程图局部的2D图像数据序列作为问题的基本输入，并将其表示为x′[n]∈RMr×Ma，其中n＝1,2,···,N是图像序列的快拍(或帧)时刻，Mr和Ma分别是图像距离维和方位维的尺寸，N是图像序列的总快拍数。通过将x′[n]按列堆叠并拉伸为列向量，可获得一般化的待分离数据x[n]∈RM×1，其中M＝MrMa。在混响干扰背景相邻快拍间具有一定相干性的条件下，根据混响子空间的动态可变性，可将问题表示为批处理的离线模型或实时的在线处理模型。

2.1 矩阵式离线表示

当混响子空间是近似不变的低秩子空间时，我们考虑问题的离线表示模型[1]。将所有待分离的快拍数据x[n],n＝1,2,···,N重新组织为离线数据矩阵

为了对该矩阵进行有效分解，通常假设它由低秩的混响、稀疏的运动目标回波和噪声成分构成，也即

2.2 向量式在线表示

其中，λ是正数的正则化标量因子。尽管有了在线分解问题，但在实践中发现，混响成分本身的低秩性，以及混响子空间的动态更新估计对分解性能的影响是最为关键的，因而在在线表示中，要更多关注如何有效快速地更新混响子空间估计，而并非精确的求解问题式(5)，这一点将在后文的算法中有所体现。

3 低秩稀疏分解算法

在考察过问题的低秩稀疏表示模型后，对离线或在线分解问题，这里分别给出不同的典型算法。在这些算法中，若有需要，都假定已知或已估计得到混响主体子空间的秩r和稀疏目标回波的稀疏度k。

3.1 加速近端梯度法

为了解决式(3)的低秩稀疏分解问题，这里应用基于子空间处理的PCA方法的一个推广，这种思想在大量类似的问题中被称为稳健主成分分析(Robust PCA, RPCA)，其无需预定义秩r和稀疏度k。相应地，将加速近端梯度法(APG)算法[12,13]应用到求解式(3)的凸优化问题。首先，定义

3.2 快速数据投影法

正如前文所述，对表示式(4)实现有效分解的关键在于混响成分本身的低秩性，以及混响子空间的动态更新(跟踪)估计。这里给出的方法更像是PCA方法的在线化版本，在每一个迭代的时间快拍n上，根据估计得到的低秩混响子空间，交替进行混响子空间滤波和瞬时稀疏目标回波成分估计。

正交迭代及其变体是简单且高效地估计跟踪子空间的手段[9]。为了估计具有大特征值的混响主导成分M×r的子空间Un，且使算法能够自适应地在线实现，考虑如式(9)的估计

表1 用于求解低秩稀疏矩阵分解问题的APG算法

表2 用于求解低秩稀疏在线分解问题的FDPM算法

4 试验结果和讨论

通过主动声呐湖上试验验证所提目标增强方法在实际的水声环境中的性能。试验中主动声呐平台安放在某一试验船上，接收阵为8元矢量水听器线列阵，由声压p，振速vx和vy一并构成24通道接收，阵列导向矢量由试验测试获得。主动发射信号为线性调频信号，由于试验条件的限制，试验中主动平台是近乎静止的，为了验证所提方法的有效性，在近距离试验混响数据中注入了一个与主动平台具有相对运动的目标回波信号(信混比-5 dB)，生成总帧数(或总周期数)为N＝60的合成阵列接收数据，目标起始坐标为(450m,140°)，终止坐标为(525m,150°)，坐标在逐帧间均匀变化。

4.1 低秩性分析

在本小节，对常规空时处理(CST)相应的近程目标方位历程图的低秩性进行分析。图1给出了基于所有N帧接收数据的方位历程图构成的离线数据矩阵X ∈RM×N的低秩性分析结果。

离线数据矩阵X的每一列是瞬时快拍数据x[n]，对于这里所关心的分离问题，离线数据矩阵各列间的相关性越强，那么其低秩性就越强，通常所能产生的分离性能也越佳。以离线数据矩阵的奇异值分解来研究矩阵各列间的相关性，图1给出了离线数据矩阵X的两种成分的奇异值分布结果。尽管不严格，但可以认为混响成分是近似低秩的，这符合本文方法可行性的前提假设。

图 1 离线数据矩阵 X的奇异值分布

4.2 目标回波增强性能

尽管两种方法通过低秩稀疏分离手段都在一定程度上抑制了混响干扰，有效地增强了目标回波，但二者在分离性能和可实现性上是有差异的。图2(a)是离线APG算法的低秩稀疏分离结果，可以看到，算法分离出的稀疏成分s中具有更少的混响干扰，但同时s中的真实目标回波亮点强度损失也较大。尽管离线APG算法在平稳的混响结构下通常具有更好的分离性能，但这里实际可能起伏的混响结构减弱了离线数据矩阵X的低秩性，使得算法分离出平滑混响干扰背景的同时，也损失了目标回波亮点的强度，这也体现了离线APG算法的稳健性较差，受模型失配影响更显著。另外，分离结果s中可能仍存在很多的混响干扰影响真实目标的判别，但通过图2(b)的合成手段，在合成的s¯子图中看到了一个明显匀速直线运动的目标轨迹，这有助于真实目标的判别，但同样的手段并不适用于原始的待分离数据X，它们的合成结果x¯难以直接揭示目标轨迹。在可实现性上，APG算法需要设置大量的参数，且某些参数对算法的性能影响显著(如正则化参数λ和µ¯)，因而在性能稳健性上也相对较差。

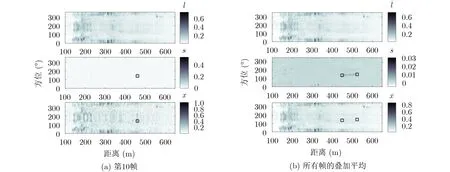
图 2 离线APG方法的低秩稀疏矩阵分解

图 3 在线FDPM方法的低秩稀疏分解

图3是在线FDPM算法的低秩稀疏分离结果，由图3(a)可以看出，其分离出的稀疏成分s中真实目标回波亮点强度损失很小，但仍存在较多的未能抑制(或分离)的干扰亮点，这一点也展现在了合成的图3(b)中。这样的结果是可以理解的，因为如前所述，在线FDPM算法可以认为是PCA方法的在线化实现版本，由于在线化实现的特点，可以期望FDPM算法具有跟踪混响主成分子空间的能力，因而当X中的混响结构存在起伏变化时，在线FDPM算法的性能可能优于离线APG算法的性能。此外，在可实现性上，在线FDPM算法同样只需要设置秩和稀疏度参数，其性能是较为稳健的。由于算法是在线实现的，因而对每次输入的快拍数据x[n]，只需少量的计算更新算法。

表3总结了应用分离算法前后目标和混响强度的对比。可以看到，在原始待分离数据x中，目标幅度很大，但目标之外的混响平均幅度也很大，综合图2和图3，此时难以判别真实目标。经APG算法滤波分离后，稀疏成分s中目标幅度相较于混响平均幅度减小要少得多，即提高了信混比，利于后续检测；FDPM算法的滤波结果同样提高了信混比，且相比APG算法目标幅度损失更小，但产生的混响干扰背景不如其均匀，因而可能产生更多的虚假目标。最后，离线APG算法更适合于事后处理机制，即同时得到了大量快拍数据，并希望比只利用少量快拍数据获得更好的滤波分离性能；在线FDPM算法更适合于实时处理机制，每一新的快拍数据输入，都会基于历史数据对其进行滤波分离，因而它处理的混响低秩子空间可以是变化的。

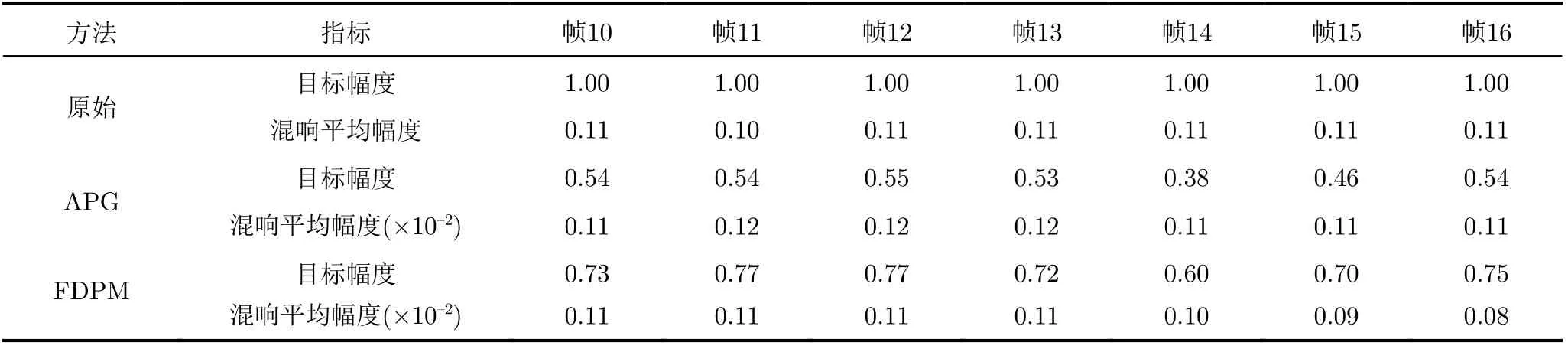
表3 应用分离算法前后目标和混响强度对比(归一化单位)

5 结论

在运动平台主动声呐近程目标的方位历程图中，针对强混响影响真实目标回波亮点判别的问题，本文设计了两种基于低秩稀疏分解的目标回波增强方法，并对其性能进行了试验讨论和分析。结果表明数据分离可行性的前提假设，即低秩稀疏性是近似成立的，此外两种方法均能有效地实现混响抑制和目标回波增强。就分离性能而言，离线APG算法在低秩且平稳的混响结构下具有更好的分离性能，但其稳健性较差且运算复杂度较大；在线FDPM算法对起伏的混响结构具有更好的适应性，稳健性较好且运算复杂度较小，但通常存在较多未能滤除的干扰亮点。在实际应用中，可以根据需求和限制选取更适宜的分离方法。