双关节刚性机械手自适应容错控制系统设计与仿真

北京联合大学机器人学院 牛瑞燕 殷莺倩 张雅婷

针对一类存在执行器故障的非线性系统，将自适应控制和容错控制相结合，在执行器部分故障情况下设计出了自适应律和控制律，对双关节刚性机械手进行了控制。利用Lyapunov的分析方法证明了所设计控制器的渐进稳定性，最后在Matlab下进行了仿真实验。仿真结果表明，系统能克服扰动且在执行器部分故障下可良好地跟踪速度以及位置信号，验证了该算法的可行性和有效性。

所谓容错控制是指当控制系统中的某些部件发生故障时，系统仍能按期望的性能指标或性能指标略有降低的情况下，还能安全地完成控制任务。在实际工程系统中，系统执行器故障发生的时间在大多数情况下是未知的，并且它的进一步发展可能导致整个系统产生不同形式和规模的故障。因此，容错控制系统设计是一种用来提高系统的安全和可靠的程度重要的手段。

随着现代工业的快速发展，人们对机器人的要求越来越高。为保证机器人在复杂的未知环境下顺利完成任务，必然要求具有容错控制能力。容错控制方法是机器人控制系统中的一种重要方法。控制系统中的各个部分，执行器、传感器和被控对象等，都有可能发生故障。在实际系统中，由于执行器繁复的工作，所以执行器是控制系统中最容易发生故障的部分。

对于非线性系统执行器故障的容错控制问题已经有很多有效的方法，其中，自适应补偿控制是一种行之有效的方法。提高整体系统的性能，保证执行器故障下大系统的稳定性也逐渐得到学者们的重视和研究。在这种背景下，对系统执行器故障状态下的容错控制进行研究具有重要的意义和应用价值。

本文针对一类存在执行器故障的非线性系统，将自适应控制和容错控制相结合，在执行器部分故障情况下设计出了自适应律和控制律，对机器人双关节刚性机械手进行了控制研究。

1 机器人双关节机械手数学模型

机器人技术在当今时代是一个非常重要的研究领域，处于科技发展的前端，所以受到了各国的普遍关注和重视，并且这已经成为了衡量一个国家机械制造业以及科技发展的水平的重要标志。

1.1 系统描述

一个典型的机器人双关节刚性机械手示意图如图1所示，不考虑摩擦力情况下动力学模型为：

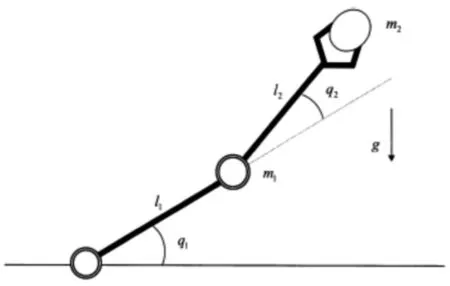
图1 双关节刚性机械手示意图

其中，q为关节位移量，M(q)为正定质量惯性矩阵，为哥氏力、离心力，G(q)=Kq为重力，T为控制力矩，w为外加干扰。

其中T为控制输入，并且有：

其中，σ是执行器的失效程度，取值范围为[0，1]，有两个执行器，则失效程度分别为σ1、σ2。

1.2 控制律设计和稳定性分析

取qd为指令，e=qd－q为误差信号。设计滑模面为：

则：

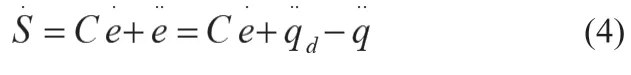
则：

取：

则：

设计控制律和自适应律为：

其中，

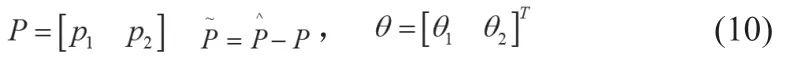
取sgnθ=1，则：

由于V ≥0，，则V有界。

即：

当t → ∞时，由于V(∞)有界，则有界，则有当t →∞时，S →0，从而有e →0，。

2 仿真分析

双关节机器人系统(不考虑摩擦力)的动力学模型为：

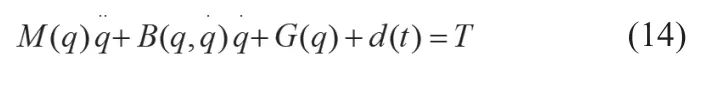
其中：

其中，两个关节的位置指令分别为q1d=sin(πt)和q2d=sin(πt)，系统的初始状态为，取，采用控制律和自适应律采用式9，k=5，γ=10。当仿真时间t=5时，取σ =0.5。仿真结果图2所示。

图2 两个关节的位置跟踪和速度跟踪

从图2可知，在系统开始仿真的时，轨迹跟踪曲线有较大的误差，但随后就逐渐跟踪上输入信号。在时间为5s的时候系统发生故障，经过自适应容错控制作用，位置输出和速度输出最终都能跟踪上系统的输入值，最终输出的曲线几乎于输入完全重合，证明了系统的有效性。

结论：本文综合考虑外部扰动和执行器故障对双关节刚性机械手影响，设计了一种自适应容错控制器，对提出的算法进行稳定性分析和仿真验证，取得了较好的控制效果，验证了算法的有效性和可实现性。