考虑通信时延与中断的省地协同异步式潮流计算

朱怡莹，周荣生，林文硕

(广东电网有限责任公司广州供电局，广州510630)

0 引言

随着配电网分布式电源的高速发展，省级电网(输电网)和地级电网(配电网)的有功功率和无功功率相互渗透，均可实现双向流动，大大增强了省地电网间的耦合关系[1]。目前，我国采用的是分级分层的调度模式，上下级调度机构之间以各自独立的形式进行调度控制，省级调度部门(省调)一般将地级电网(地调)等值为负荷，而地级电网将省级电网等值为电压恒定的电源。这种潮流计算方法忽略了省地电网间的耦合性，随着分布式电源的大量接入，将产生不精确的计算结果[2]。因此，在分布式电源广泛接入的背景下，需研究省地协同的一体化调度架构和调度模式，才能精确、有效地处理省地电网间的耦合性。

近年来，很多学者针对省地协同、输配协同潮流计算开展了研究，求解算法总体上可以分为分布式求解[3 - 7]、等值法求解[8]、全局模型[9]求解3类。关于分布式求解，文献[3 - 6]提出利用主从分裂模型对输配网进行建模，通过输电网和配电网的交替迭代算法实现全网的潮流计算，这种方法能够有效地实现分布式计算，保障了输配电网调度部门各自的信息安全，但存在潜在的收敛性问题。文献[7]为了改进主从分裂模型及其求解方法存在的收敛性问题，提出了一种基于连续交叉点估计的求解方法，在大量分布式电源渗透、有载变压器分接头调节等情景下，均能够取得较传统主从分裂方法相比更高的收敛性能和计算效率。在等值法求解方面，文献[8]提出了一种基于配电网等值的输配协同潮流计算方法，在保证一定精度的条件下提高了计算效率，但这一等值方法只适用于不含或只含PQ控制的配电网，无法对含有PV控制的配电网进行精确的等值。在全局模型求解方面，文献[9]提出将省地电网模型进行拼接，并通过Levenburg-Marquardt算法进行求解，提高了潮流计算的鲁棒性，但是这一方法需要依赖统一的数据平台，如调控云等[10 - 12]。这些统一的平台目前尚处于发展阶段，且由于全局模型存在规模庞大、数值稳定性差等潜在问题，全局模型在省地协同潮流计算的可用性尚不明朗。

由此可见，3种模型和求解算法各有优劣，但分布式模型及其求解算法在目前的调度模式下最为实用，且能较好地处理配电网中分布式电源的影响。但另一方面，分布式算法往往需要省调和地调频繁的信息交互，因此省调和地调的通信条件高度影响着分布式算法的性能。之前的文献一般在理想的通信条件下进行研究，即不同调度部门系统之间通信时延忽略不计[3 - 8]。显然，这一假设并不符合实际的工程条件。

基于此，本文提出了一种考虑通信条件的省地协同异步式潮流计算。具体来说，本文提出了一种“部分同步”的概念用以提高潮流计算在考虑通信时延条件下的计算效率。在省地电网交替的每一次迭代过程中，省级电网调度部门无需等待所有地级电网的计算结果，而只需要接收部分地级电网调度部门的数据，便可以进行异步潮流计算。面对通信中断的情形，本文提出了一种基于历史数据的配电网等值模型，即在某一地级电网调度部门出现非瞬时中断时，省级电网调度部门可以通过历史数据建立该低级电网调度部门管辖的配电网的近似模型，从而保证省级电网调度部门管辖的输电网区域潮流计算能够顺利完成。

算例测试验证了本文算法的有效性，因此，本文的研究成果将为未来省地协同运行特别是省地协同的潮流计算提供重要的理论和实践基础。

1 省地协同同步式潮流计算

省地协同同步式潮流计算主要以主从分裂理论为基础，建立输配电网异构模型，通过省地两级电网的交替迭代实现分布式的潮流计算。

1.1 输配电网异构模型

图1为输配一体化电网的异构模型示意图[4,7]。如图1所示，这个电网被分成了一个输电网部分、若干配电网部分和边界部分。其中，输电网部分由省级电网调度部门进行管理，不同的配电网部分由不同的地级电网调度部门进行管理，而边界部分由输配网边界节点(即配电网根节点)组成，由省、地级电网调度部门协作管理。

图1 输配电网异构模型Fig.1 Heterogeneous model of transmission-distribution networks

基于主从分裂理论[4]，可以建立全局潮流方程，式(1)—(2)分别表示输电网潮流方程和配电网潮流方程，具体如式(1)—(2)所示。

(1)

(2)

1.2 算法流程

1)省级电网调度部门运行算法

2)第i个地级电网调度部门运行算法

步骤4：等待省级电网调度部门的数据，若为终止算法信号，则终止算法；否则，令k=k+1，返回步骤2。

2 考虑通信时延省地协同异步式潮流计算

根据1.2节中介绍的省地协同同步式潮流计算流程不难发现，在每一次迭代中，省级电网调度部门都需要等待所有地级电网调度部门的更新数据。这意味着，如果有一些地级电网调度部门，计算速度缓慢，或与省地电网调度部门之间通信条件恶劣，将严重拖慢省地协同整体的潮流计算流程。因此，考虑设置省级调度部门时钟与地级调度部门时钟，引入部分协同的概念，从而得到考虑通信时延的省地协同异步式潮流计算方法。

2.1 省级调度部门与地级调度部门时钟

2.2 部分同步

在同步式算法中，省级电网调度部门的每1次迭代都需要等待所有的地级电网调度部门的更新数据，这使得一些速度缓慢、通信条件恶劣的地级电网调度部门严重制约了整体的计算效率。为了缓解这一问题，引入“部分同步”的概念来替代原来的完全同步。具体说来，省级调度部门在每1次迭代中只需要等到来自S个地级调度部门的更新，即可开始接下来的计算。这里，S在1～N之间。特别情况下，同步式算法可以视作S=N的情形。

在“部分同步”的模式下，那些速度缓慢、通信条件恶劣的地级调度部门传送更新数据到省级调度部门的频率将远小于那些速度快、通信条件良好的地级调度部门。这虽然大大提高了省级电网计算更新的效率，但也降低了数据的实时性。为了保证在迭代过程中各地级调度部门上传的数据具有较好的实时性，这里引入1个最大延迟轮数的概念。具体说来，省级调度部门每进行τ次迭代，每1个地级调度部门至少更新传送数据至省级调度部门1次。这里，τ≥1。

2.3 算法流程

基于上述的“部分同步”机制，在省地协同异步式潮流计算中，将式(1)—(2)改写为式(3)—(4)。

(3)

(4)

具体迭代算法如下，其中Φk表示在省级调度部门时钟为k时已经完成更新并传送数据到达省级调度部门的地级调度部门的集合。显然，当S=N或τ= 1时，异步式潮流计算退化为同步式潮流计算。

1)省级电网调度部门运行算法

步骤4：对于i∉Φk， 令τi=τi+1。

2)第i个地级电网调度部门运行算法

步骤4：等待省级电网调度部门的数据，若为终止算法信号，则终止算法；否则，令ki=ki+1，返回步骤2。

2.4 收敛性分析

首先，省地协同同步式潮流计算的收敛性在文献[4]中已经进行了详细分析，为同步式潮流计算的局部收敛性提供了充分性条件。这个结论也可以应用到异步式潮流计算中，可以分析异步式潮流计算的收敛速率。

假设省级调度部门已经进行了T次迭代。令：

(5)

(6)

式中N为迭代次数。

在异步式潮流计算中，地级调度部门数据的传送和接收是具有不确定性的，取决于许多因素，特别是通信条件。为了分析方便，假设在省级调度部门时钟为k的时候，N个地级调度部门的更新有同等的概率到达省级调度部门。

故在异步式潮流计算中，式(6)可以推广如式(7)所示：

(7)

式中E(·)为数学期望函数。

这一表达式说明，异步式潮流计算的收敛速率是受到N、τ和S影响的，具体如下：

1)N越大，则收敛速度越慢，这是因为省级调度部门需要与更多的地级调度部门交换信息，并在不断迭代的过程中达到收敛条件；

2)S越大，则收敛速度越快，这是因为在省级调度部门的每次迭代过程中，有更多的地级调度部门的数据信息到达了省级调度部门；

3)根据“部分同步”机制，在省级调度部门的T次迭代中，每1个地级调度部门的数据信息至少更新并传送到省级调度部门T/τ次。因此，τ越大意味着最慢的地级调度部门更新数据的频率越低，因此收敛速度越慢。

3 基于历史数据的配电网等值模型

异步式潮流计算方法能够缓解部分极端缓慢的地级调度部门对整体计算效率的负面影响。然而，当省地电网调度部门之间发生非瞬时性通信中断时，上述的异步式潮流计算方法仍然会失效。因此，为了进一步提高省地协同潮流计算的鲁棒性，本文提出了一种基于历史数据的配电网等值模型，并应用至省地协同潮流计算中。特别说明，在本文中假设地级调度部门管理的配电网仅含PQ节点。

3.1 多项式等值

考虑到配电网在绝大多数情况下呈现辐射状运行。在仅含PQ节点的情况下，不难证明，注入配电网根节点的有功、无功功率是根节点电压幅值的单调函数[8]。因此，多项式等值适用于近似表示它们之间的函数关系。对于省级调度部门，在与第j个地级调度部门的边界节点处，有功功率Pj(Uj)和无功功率Qj(Uj)可以表达为式(8)—(9)。

(8)

(9)

式中：m为多项式阶数；Uj为边界节点的电压幅值；ai和bi为拟合的多项式系数。通常，m=2已经可以达到较高的精度。

3.2 算法流程

首先，对于每一个地级调度部门，在当前的运行方式下，基于历史数据通过式(8)—(9)的方式，拟合得到2个近似函数并保存，以备省级调度部门的全局潮流计算指令。在省地协同潮流计算的过程中，省级调度部门首先向各地级调度部门发送潮流计算指令。地级调度部门在接收到潮流计算指令后，将其第一次迭代结果与离线拟合的近似函数的多项式系数传送至省级调度部门。

后续潮流计算过程中，若不发生非瞬时性的通信中断，则与2.3节中的算法流程一致。若在后续潮流计算过程中，省地调度部门间的通信网络发生瞬时性故障，则省级调度部门在后续的迭代过程中，利用本地存放的多项式系数构建近似函数，作为断开通信的地级调度部门管辖的配电网的等值。具体的计算流程如下。

步骤4：对于i∉Φk， 令τi=τi+ 1。

4 测试结果

本节通过一个输配网耦合的测试系统来验证所提算法的有效性。该测试系统通过拼接IEEE 57节点的输电网算例和16个PG&E 69节点配电网算例得到(输电网的5、10、13、51、15、16、17、18、19、20、23、25、27、53、29、30号节点分别通过一个变压器接入一个69节点配电网)。潮流计算的收敛要求设定为10-6p.u.。省级电网调度部门管理该57节点输电网，16个地级电网调度部门分别管理16个配电网。省地电网调度部门之间的通信网络随机设置10～150 ms的通信时延。

4.1 精确性测试

首先，需要验证所提出的异步式潮流计算结果的精确性。图2比较了在异步式潮流计算与传统同步式潮流计算下省级电网57个节点的电压幅值。显然，在规定的收敛精度下，两种计算方法可以取得相同的结果，这有效地验证了本文所提出的异步式潮流计算的准确性。

图2 计算精度对比Fig.2 Calculation accuracy comparison

4.2 收敛性测试

图3展示了在不同的参数配置下省地协同异步式潮流计算的迭代次数。不难发现，在S较大或τ较小时，异步式算法趋近于同步式算法，此时迭代次数趋近最低。而当S越小或τ越大，则异步式算法所需的收敛次数也就越多。这一结论验证了2.4节对本文所提出的算法的收敛速度的分析。

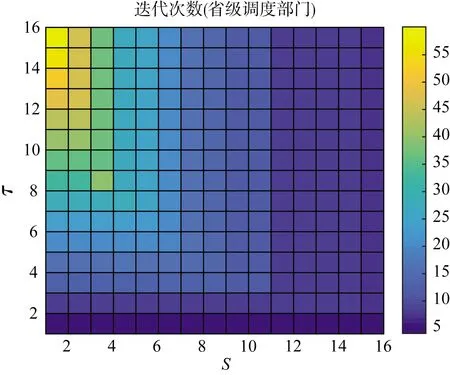
图3 异步式潮流计算的迭代次数Fig.3 Iteration number of asynchronous power flow calculation

4.3 计算效率测试

虽然异步式算法较同步式算法往往需要更多的迭代次数，但这并不意味着它们的计算效率更低。图4展示了在不同的参数配置下省地协同异步式潮流计算的计算用时。不难发现，在S较大或τ较小时，异步式算法趋近于同步式算法，此时的计算用时比较多，这正是由于前文中分析的部分地级调度部门与省级调度部门之间的通信网络状况比较差，通信时延较长。在传统的同步式潮流计算中，这些地级调度部门的存在严重制约了整体的计算效率。而当S小于10、τ大于2时，异步式算法在计算效率方面的优势最为明显，总体计算耗时能控制在550～650 ms，这相比同步式算法900 ms左右的计算用时有显著降低。这也说明了合理地选择S和τ能充分发挥异步式算法的计算效率。

图4 异步式潮流计算的计算用时Fig.4 Time consumption of asynchronous power flow calculation

4.4 配电网等值测试

为了测试配电网等值的效果，历史数据通过蒙特卡洛模拟的方法生成：令配电网的根节点电压幅值在0.9 p.u.和1.1 p.u.之间随机取值，计算根节点注入功率，形成历史数据。需要指出的是，在实际调度运行中，可以通过数据库中大量历史数据完成。

表1展示了在不同的非瞬时中断发生的情况下，基于等值模型进行异步式潮流计算带来的偏差。表1中max|ΔU|指的是计算得到的输电网电压中节点电压幅值的最大绝对误差，j表示第j个地级调度部门与省级调度部门之间发生非瞬时性中断。

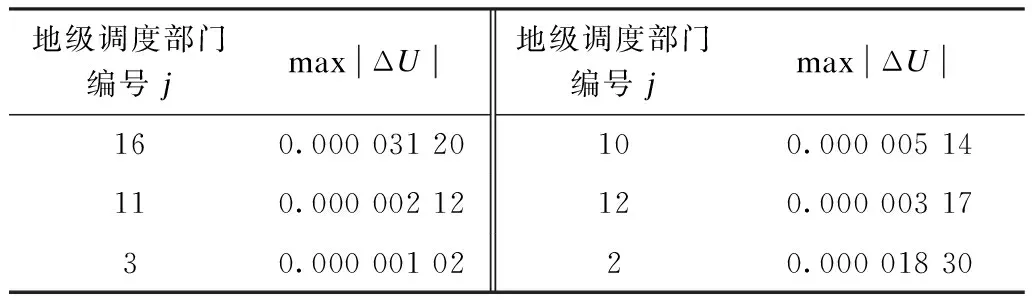
表1 基于配电网等值的潮流计算误差Tab.1 Calculation error under distribution-network-equivalencing- based power flowp.u.

如表1所示，本文所提出的配电网等值方法二次多项式能够取得很高的精度，在不同地级调度部门发生通信中断时，输电网潮流计算结果中的节点电压幅值的误差均小于0.000 05 p.u.，这一精度基本满足的实际调度中所需求的计算精度。

5 结论

本文提出了一种基于“部分同步”机制的省地协同异步式潮流计算，并提出一种配电网等值方法。通过测试算例的验证，可以形成如下结论。

1)本文提出的异步式潮流计算方法可以取得与传统同步式方法完全相同的计算精度；

2)相较于传统的同步式计算方法，通过引入“部分协同”机制，设置合理的S和τ能显著提高计算效率。S和τ的具体选择与通信网络的状况息息相关，一般可以通过数值时延来进行确定；

3)本文提出的配电网等值方法适用于仅含PQ节点的配电网，多项式拟合简便、易操作，精度较高，将其应用在省地协同的异步式潮流计算中，节点电压幅值的误差控制在0.000 05 p.u.以内。

综上可知，本文所以提出的方法在省地调度部门之间的通信网络不稳定或发生非瞬时中断时，具有工程实用性。