基于小气候舒适度的城市景观带景观元素配比MATLAB寻优

黄弥儿

(广西交通设计集团有限公司，广西 南宁 530029)

0 引言

植物、水体和各种软硬铺装是城市开放空间景观材料的基本三元。植物、水体和软硬铺装对热环境、湿环境、风环境的调节作用，其整体效应表现为对人体热舒适感受的影响[1,2]。然而，片面过度增大任何一种景观元素的配比，都不利于风景园林小气候的改善以及人体热舒适的提升，合理适宜的景观元素配比才是提高风景园林小气候舒适度的有效途径。

景观元素对小气候舒适度的影响，除了各景观元素的独立作用，还存在不同景观元素联合起来的协同影响。城市景观带植物、水体及软硬铺装配比组合的寻优问题，实际上是一个如何合理选择植物、水体和软硬铺装配置比例，使小气候舒适度指标达到目标值的优化设计问题。

本研究尝试在小气候因子实测和热舒适分析评价的基础上，通过数学建模，以生理等效温度(Physiological Equivalent Temperature，PET)为优化目标，以乔灌木、水体、草坪和硬质铺装的配比为优化变量，运用非线性规划的优化设计方法，借助MATLAB优化工具进行优化求解，给出满足夏季小气候舒适度目标的城市景观带景观元素配比参考值。

1 小气候因子实测及数据采集

研究分别在上海世博公园中部的卢浦大桥东西段和陆家嘴滨江带东部的上海船厂滨江绿地段，两处各选取8个测点，以测点为中心、半径为10m的范围为样本空间，进行户外小气候实测。根据气象历史数据，实测选择在持续高温天气较为集中的7、8月份，平均气温高达33～36℃的白天时段进行。采集数据包括空气温度、相对湿度、风速风向及太阳辐射等小气候因子。测试仪器为Watchdog 2000便携式小型气象站，实测时将其安装在三脚架上，离地高度为1.5m，采集时长为每天8:30—17:30，间隔时间设置为每15min自动采集一次数据。

2 景观元素配比优化目标确定

本研究采用生理等效温度PET作为小气候舒适度评价指标，并将所得舒适的PET值范围作为景观元素配比的优化目标。PET是目前普遍使用，而且被认为是最适用于户外人体热舒适评价的客观评价指标，通常用于研究不同地区热中性温度和中性温度范围。利用小气候因子实测数据，在RayMan 1.2上，置入试验地的地理信息，并按照性别man、身高175cm、体重75kg、年龄35周岁、服装热阻0.5clo及活动量80w的人体参数设置，计算测点的PET值(表1)。

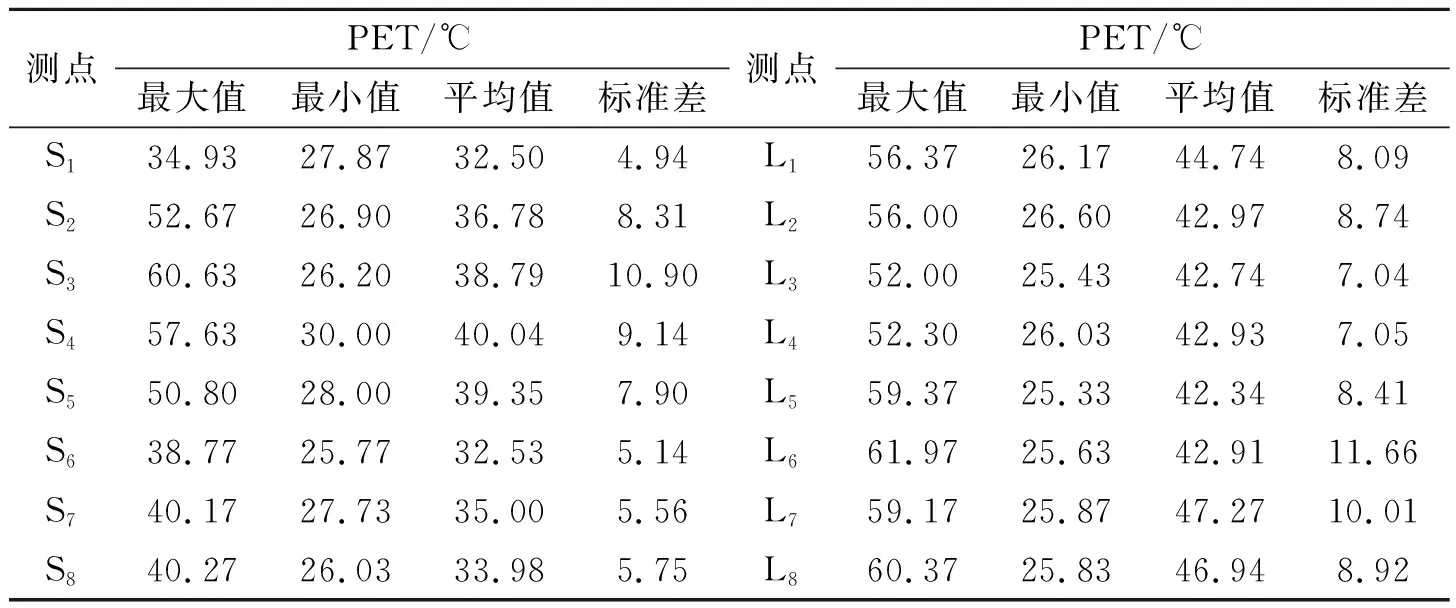
表1 上海世博公园和陆家嘴滨江带实测点PET值

为获得人们实际的热舒适感受，以确定景观元素配比寻优的PET目标，在小气候实测基础上，通过热感觉投票(Thermal Sensation Vote，TSV)和热舒适投票(Thermal Comfort Vote，TCV)调查，进行热舒适分析与评价。计算结果得，夏季极端天气条件下，上海城市景观带户外热中性温度为19.2℃，热中性温度范围为14.5～23.9℃，小气候舒适度范围为7.12～28.5℃(表2、表3)。

表2 上海城市景观带夏季PET热感觉评价标准

表3 上海城市景观带夏季PET热舒适评价标准

由RayMan 1.2计算所得的PET值(表1)显示，PET最小为32.50℃，已经超出28.5℃的舒适值范围。表明在夏季极端天气条件下，上海城市景观带白天户外小气候环境基本上是不舒适的。对小气候热舒适度的评价，原则上应是PET值越小越好，PET值越小，说明不舒适程度越低，空间景观元素配比对小气候舒适度的改善作用越强。由此确定PET最小值作为景观元素配比的优化目标。

3 小气候舒适度与景观元素配比回归建模

分别以乔灌覆盖率(Arbors and Shrubs Proportioning，ASP)、水体占地率(Water Proportioning，WP)、草坪覆盖率(Grass Proportioning，GP)和硬质铺装率(Hard Pavement Proportion，HPP)作为各测点样本空间植物、水体及软硬质铺装景观元素配比的测定指标。样本空间范围确定为以实测点为圆心、半径为10 m的圆形区域，利用红外线测距仪、Google Earth Pro、CAD、Are GIS等测量和计算景观元素的配比值。

根据相关文献，参考常见园林绿量计算方法，乔灌覆盖率取样本空间内大小乔木和大灌木树冠垂直投影面积总和与空间总面积的比，水体占地率取样本空间内各类水体面积总和与空间总面积的比，草坪覆盖率取样本空间内各类草本植物及低矮小灌木投影面积总和与空间总面积的比，硬质铺装率取样本空间内的道路和广场等的硬质铺装面积总和与空间总面积的比。计算结果见表4、表5。

表4 上海世博公园实测点样本空间景观元素配比测定结果

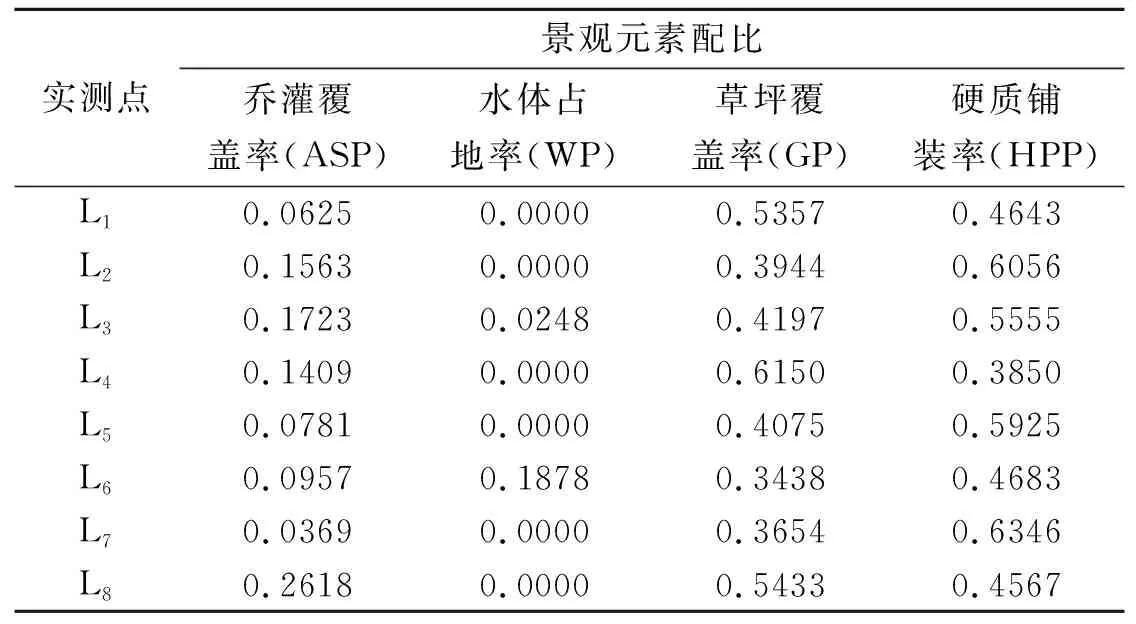
表5 上海陆家嘴滨江带实测点样本空间景观元素配比测定结果

以样本空间景观元素配比为自变量，以PET为因变量，利用表1的PET平均值和表4、表5的景观元素配比数据，进行回归方程拟合，建立PET关于乔灌覆盖率、水体占地率、草坪覆盖率、硬质铺装率的多元非线性回归方程见式⑴。

PET=-22.329ASP2+18.280WP+108.961GP-76.123GP2+37.689HPP2

⑴

式中：PET：生理等效温度;ASP：乔灌覆盖率;WP ：水体占地率;GP ：草坪覆盖率;HPP：硬质铺装率。

表6～表8为对回归方程的评估。结果显示，所建立方程拟合程度高，回归效果好，解释能力强，能够保证由方程解出的各景观元素配比值具有较高精度和可靠性。

表6 模型汇总表

表7 方差分析表

表8 回归系数表

4 景观元素配比组合MATLAB 优化求解

本研究运用MATLAB软件，通过非线性规划方法进行优化求解。MATLAB是目前许多工程领域中广泛用于数学分析计算和图像图形处理的科学计算软件。MATLAB具有十分强大的计算功能，可以解决工程应用中的很多数学问题。MATLAB内带有数十种能够完成各种数学计算的工具箱，其中的优化工具箱能够提供多种优化算法，是求解优化设计问题非常有效的工具。

MATLAB在景观领域也有应用，主要用于图像分析处理和评价预测模型建立。常用的图像处理方法包括图像的读入显示、图像增强以及图像分割[3-5]。评价预测模型的建立则是调用统计学工具箱或曲线拟合工具箱等，在命令窗口输入相应的参数和命令，最终输出结果。其原理与SPSS的回归建模相似，但操作方法因软件而异。而寻优工具在景观方面的应用多集中于大尺度的景观生态学研究[6,7]。

4.1 目标函数

非线性规划的数学模型一般表达为：

(2)

式中：X=(x1，x2，…，xn)T是n维空间En中的向量，f(X)为目标函数，hv(X)为m个等式约束条件，gu(X)为n个不等式约束条件。

非线性规划解决的是一类目标函数或约束条件有一个或者多个是自变量的非线性函数的极值问题。本研究对城市景观带景观元素配比的寻优，是在有限空间内和一定约束条件下，满足PET值最小的景观元素配比最优组合设置问题。目标函数为PET与各景观元素配比的多元非线性回归方程，函数式见式(1)。

4.2 设计变量

选择乔灌覆盖率、水体占地率、草坪覆盖率、硬质铺装率为设计变量，并且令：

X=[x1，x2，x3，x4]T=[ASP，WP，GP，HPP]T

(3)

4.3 约束条件

约束条件主要考虑以下两个方面，一是景观元素配比的取值区间，二是景观元素的空间限制条件。景观元素配比的取值区间为0～1之间，某一景观元素配比的变动范围介于有限空间内完全没有或完全覆盖两种情形之间。并且基于植物种植生长的空间要求,设定以下两个假设条件：(1)乔灌木、草坪及硬质铺装均不与水面重叠；(2)乔灌木可以种植覆盖在草坪和硬质铺装上。

整理以上条件可得到的约束条件式(4)表达。

(4)

4.4 优化求解

本研究利用MATLAB软件中的fmincon函数工具箱进行优化求解。fmincon是MATLAB优化工具箱中的一个优化函数，通过直接调用的方式，可以解决有约束条件下的非线性多变量优化问题。fmincon函数是将非线性优化问题转化为二次规划问题，使用非线性规划中的系列二次规划算法来求解。利用fmincon函数求解有约束的多元非线性函数最小值，其数学模型一般描述表达为式(5)。

(5)

式(5)中：minf(x)：目标函数;c(x)≤0：不等式函数;ceq(x)=0：等式函数;A·x≤b：线性不等式约束条件;A：线性不等式约束系数矩阵;Aeq·x=beq：线性等式约束条件;Aeq：线性等式约束系数矩阵;lb、ub：优化变量x的边界约束。

fmincon函数的调用格式为：[x,fxal,exitflag,output]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub)

由此得到基于PET最小的景观元素配比寻优的数学模型：

minf(X)=PET=-22.329x12+18.280x2+108.961x3-76.123x32+37.689x42

(6)

分别取初始设计参数为:X(0)=[1,1,1,1]T和X(0)=[0,0,0,0]T

(1)编写目标函数的M文件fun1.m，返回x处的函数值

f：function f=fun1(x)；

f=-22.329*x(1)2+18.280*x(2)+108.961*x(3)-76.123*x(3)2+37.689*x(4)2

(2)设置线性约束的等式和不等式系数：Aeq=[0 1 1 1] ；beq=1；A=[1 0 -1 -1] ；b=0；

(3)给定初始值和变量的上下限约束并调用优化过程。

①X0=[1 1 1 1]；

②X0=[0 0 0 0]；lb=[0 0 0 0]；ub=[1 1 1 1]；[x,fxal,exitflag,output,lambda]=fminc('fun1',x0,A,b,Aeq,beq,lb,ub).

(4)运行程序得计算结果为：

①X=1.0000，5.7846e-09，1.0000，1.6030e-08;fval=10.5090.

②X=0.5951，0.4049，6.2396e-09，0.5951;fval=12.8412.

5 总结讨论

由MATLAB程序运行结果得，初始设计参数取X(0)=[1,1,1,1]T时，水体占地率和硬质铺装率均很小约等于0，乔灌覆盖率和草坪覆盖率等于1，PET最小值为10.51℃；初始设计参数取X(0)=[0,0,0,0]T时，乔灌覆盖率等于0.5951，水体占地率等于0.4049，草坪覆盖率很小约等于0，硬质铺装率等于0.5951，PET最小值为12.84℃。将运行结果数据圆整后得到优化结果见表9。

表9 用数学规划法寻优的最佳景观元素配比组合优化结果

大量研究表明，MATLAB的fmincon作为一种局部优化函数，优化结果很大程度依赖于初始值的选择；尤其是对非线性显著的多变量优化问题，受初始值影响，一般存在多个局部最优解，优化求解只能找到离初始点最近的极小值。因此，初始值的选择合适与否是得到全局最优解的关键所在。初始值的选取无固定准则，一般依据变量满足的物理、数学意义和结合工程实践经验来选取。

比较两种初始值下的求解结果发现，乔灌木下层铺装的选择，依有水体和无水体，显示为全部为草坪或者全部为硬质铺装的两种情况。水体占地率为0时，优化结果是乔灌木下层铺装全部为草坪。水体占地率非0时，优化结果是乔灌木下层铺装全部为硬质铺装。说明在无水的情况下，草坪的作用优于硬质铺装的作用，相反，在有水的情况下，硬质铺装的作用优于草坪。

优化结果还显示，在有硬质铺装的情况下，需要较大的水面面积才能得到最小的PET值，或者在有水的情况下，相比于草坪，适度增加硬质铺装更有利于降低PET值。此外还发现，在寻优结果的两种配比方案中，只有乔灌草的组合有最小的PET值，而且无论有无水体，欲取得较小的PET值，乔灌木应全部覆盖草坪和硬质铺装，体现了植物小气候效应的显著性及其对热舒适度改善的优越性。

6 应用算例

以上两个配比优化结果，虽可得到最小的PET值，但取值均为一种或两种景观元素配比为零的极端情况。实际的景观设计中，以乔-灌-草-水为典型的景观空间，植物、水体、草坪及硬质铺装大多都是同时存在的。为得到比较实际的景观元素配比优化组合，通常采用中间值。因此在本应用算例中，依据世博公园和陆家嘴滨江带各测点景观元素配比的取值范围，排除取值为0的元素配比值。给定如下变量上下限，并调用优化过程，运行程序所得结果如下：

(1)X0=[1 1 1 1]；(2)X0=[0 0 0 0]；lb=[0.1 0.1 0.1 0.2]；ub=[0.7 0.5 0.8 0.9]；

[x,fxal,exitflag,output,lambda]=fminc('fun1',x0,A,b,Aeq,beq,lb,ub)

①X=0.7，0.3，0.1，0.6;fval=18.2457

②X=0.7，0.3，0.1，0.6;fval=18.2457

表10 应用算例最佳景观元素配比组合优化结果

MATLAB运行结果得，初始设计参数取0或1时，PET最小值均为18.25℃，小气候舒适度均为非常舒适。此时景观元素的配比为:乔灌覆盖率等于0.7,水体占地率等于0.3,草坪覆盖率等于0.1,硬质铺装率等于0.6。此配比可以作为城市景观带景观空间适宜的景观元素配比参考值。该算例的优化结果亦印证植物在调节小气候和改善热舒适度方面具有优越性，乔灌木覆盖率应等于草坪覆盖率和硬质铺装率之和。在有水的情况下，适度增加硬质铺装更有利于降低PET值。

7 结语

通过实测和计算，提出夏季极端天气条件下，上海城市景观带小气候舒适度评价标准，并对小气候舒适度与景观元素配比进行回归建模。在此基础上，将基于小气候舒适度的景观元素配比优化，视为一个有约束的多元非线性规划问题，采用数学规划法进行寻优，将所得回归方程作为目标函数，以乔灌覆盖率、水体占地率、草坪覆盖率、硬质铺装率为设计变量，结合一系列约束条件，利用MATLAB中的优化工具箱，通过fmincon函数进行优化求解。

寻优结果得到：⑴空间中无水时，仅有乔灌木和草坪的景观元素配比方案PET值最低，而空间中有水时，乔灌木层下全部为硬质铺装的配比方案为最优；⑵植物在调节小气候、改善热舒适方面效果更为显著，为获取较小的PET值，乔灌覆盖率应等于下层草坪覆盖率和硬质铺装率之和；⑶空间包含硬质铺装时，需要较大的水面面积才能得到最小的PET值，或者在有水的情况下，相比于草坪，适度增加硬质铺装更有利于降低PET值。

本研究将数学规划方法引入小气候研究和景观设计，从数量化的角度，为城市风景园林小气候适宜性规划设计提供理论参考和一种新的研究思路，有利于将小气候适应性规划设计中的传统经验转化为可操作调控的量化设计指导，对通过技术手段实现景观的规划设计目标具有现实意义。后续研究中，将扩大实测研究的样本空间容量，引入铺装反照率、叶面积指数等区别景观元素成分性质特征的修正系数，修正回归方程，拓展到更多更细的变量进行全局优化。