case-cohort抽样下比例风险模型中参数的逆概率加权估计*

陈丽玲，韦程东，唐璐薇，罗文婷，林玉婷，周昭君

(南宁师范大学 数学与统计学院,广西 南宁 530100)

1 引言

流行病学、生物医学和遗传学等领域的研究，经常需要长期跟踪大量的研究对象，以大范围研究疾病的病因与个体暴露因素之间的关系，获得有意义的结果. 然而，在实际研究中，一些暴露因素或关键指标的检测成本较高，给研究人员带来了很大不便.比如，在COVID-19确诊病人的治疗过程中，有些项目检测的费用是极高的(如细胞因子检测)；在非小细胞肺癌的研究中，检测个体的表皮生长因子受体的基因突变大约每人需要人民币2万元.而经费预算有限的研究人员，总是希望能够在降低成本的同时提高效率. 因此，选择一个合适的抽样方法抽取研究样本，具有理论意义和现实意义.

对于带有删失时间的事件数据，Prentice[1]提出的case-cohort抽样方法是一种可以节约成本和提高效率的有偏抽样方法，被广泛应用于各个领域.它的思路是首先从总体中随机抽取一个子列，此子列中包含了部分失效和删失的个体，之后再从该子列外的样本中抽取出所有的失效样本，最后将两次抽取出来的样本合并在一起，就得到了case-cohort样本.case-cohort抽样方法被提出后，引起了学术界的关注.用case-cohort抽样方法抽取出来的数据的统计推断主要基于似然估计方法，如在cox模型下，Prentice[1]提出了一种伪似然法；Self和Prentice[2]提出了一种修正的伪似然法，其给出的风险集仅仅由一个子队列中正在经历风险的样本组成，该文还证明了Prentice[1]的伪似然估计和其提出的修正伪似然估计是渐近等价的；钱永春、丁洁丽[3]提出了两种基于伪似然思想的统计推断方法，研究了病例队列设计的实用性和有效性.不完全观测数据的逆概率方法已被广泛应用于失效时间下的加权估计方程，例如，Kulich和Lin[4]提出的加性风险模型，Kong和Cai[5]提出的加速失效时间模型都用此法.

学者们在case-cohort抽样方法方面和似然估计方法方面的研究成果为我们提供了理论基础.然而，在上面提及的针对case-cohort抽样方法的研究中，学者们并没有考虑到采用case-cohort抽样方法会使协变量信息观测不完全且会使补充样本的分布与总体的分布不相同，使得在此时部分似然函数不能用于case-cohort抽样下比例风险模型中β的估计.对此，基于前人的研究成果，本文研究在case-cohort抽样下比例风险模型中参数的逆概率加权估计方法，通过使用逆概率加权方法修正在case-cohort抽样中协变量信息观测不完全且补充样本的分布与总体的分布不相同带来的影响，证明了逆概率加权后参数估计值的渐近性质. 此外，文章还用Newton-Raphson迭代算法进行数值模拟.

2 模型与抽样

λ(t|Z)=λ0(t)exp{βTZ(t)}，

其中λ0(t)是未知的基底风险函数，β=(β1,β2,…,βp)T是未知的p维向量回归系数，Z=(Z1,Z2,…,Zp)T是p维协变量.

{Ti,Δi,(ξi+Δi(1-ξi))Zi(t),0≤t≤Ti}，

其中，Ti表示观测时间；Δi=1表示没有删失，Δi=0表示右删失；Zi表示p维的协变量；ξi=1表示被抽中的样本，ξi=0表示没有被抽中的样本.

在生存分析的研究中，对β的推断可以基于部分似然函数

相应的部分对数似然函数为

此时参数β的极大似然估计值为

然而，在case-cohort抽样中协变量信息观测并不完全且补充样本的分布与总体的分布并不相同.因此，部分对数似然函数不能用于case-cohort抽样下比例风险模型中β的估计.此时，可以采用逆概率加权的方法来修正在case-cohort抽样中协变量信息观测不完全且补充样本的分布与总体的分布不相同带来的影响.逆概率加权的权重公式如下：

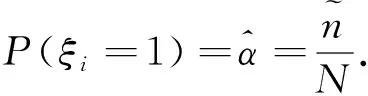
在case-cohort抽样下 ，可采用以下逆概率加权估计方程来估计回归参数β：

其中

3 渐近性质

以β0表示β的真值，表示研究的结束时间，参考Anderson & Gill的论文[6]，定义Mi(t)=Ni(t)-λi(t)dt，其中

下面给出假设条件(A1)～(A7):

(A1) 参数空间B是紧的凸集.

(A2) 协变量Z是紧集.

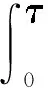
(A5) 对∀t∈[0,],有P(Yi(t)=1)>0.

(A6) 存在一个邻域B，且β∈B，t∈[0,],使得满足

(ii) 对于s(d)(β,t)(d=0,1,2),当t∈[0,]时，β是一致连续的，并且，s(0)(β,t)是有界的而且是远离零的.

(iii) 对于∀β∈B,t∈[0,成立.

(A7) 矩阵

是正定的，其中

证明设A(β,t)是cox模型在时间t上的偏似然函数的对数，即

注意到A(β,t)=ω(β,t)，因此参考Anderson & Gill[6]的渐近性质，有

X(β,t)=n-1(A(β,t)-A(β0,t))，

注意，X(β,t)依概率收敛于D(β,t)，而且D(β,t)一致收敛于d(β)，

其中，d(β)是关于β的连续凸函数，且在β0处取得唯一的最大值，即

d(β)≤d(β0).

当且仅当β=β0时，上式等号成立.

d(β*)≥d(β0)，β*≠β0.

其中

∑1(β0)=E[R1(β0)⊗2]，

∇βω(β)=0.

运用一阶泰勒展开式将上式左侧在β0处展开，可以得到

因此可得

(1)

由于

(2)

(3)

又因为

(4)

E[Ri(β0)]=0，E[(ωi-1)Ri(β0)]=0，E[(ωi-1)Ri(β0)⊗2]=0.

由于式(4)的右边是一个独立同分布的零均值随机向量的和，且其两项不相关，所以由多元中心极限定理可知

其中,

综上可得

(5)

根据Slutsky定理及式(1),(2),(5)，有

4 数值模拟

考虑以下比例风险模型：

λ(t|Z1,Z2)=λ0(t)exp{β1Z1+β2Z2}.

在每个设定下，表1和表2给出了估计偏差(Bias)、估计的样本标准均方误差(SMSE)、估计标准差(SD)、估计标准差的均值(SE)以及收敛概率为95%的名义置信区间(CP).

表1的模拟结果

表2的模拟结果

5 结论

本文讨论的在case-cohort抽样下比例风险模型中参数的逆概率加权估计方法，既解决了大样本带来的烦恼，为研究节约了成本和时间，又提高了研究效率.当然，除了本文提到的逆概率加权方法可以去掉协变量不完整观测带来的影响外，还有一种方法是时变加权方法，后续研究也可对这两种方法进行比较.