异构网络中用户关联和功率控制的协同优化*
樊 雯,陈 腾,菅迎宾
(石家庄铁路职业技术学院 信息工程系,石家庄 050041)
0 引 言
当前数据信息传输网络结构中,异构网络可有效满足移动数据流量需求的爆炸性增长,并兼具密集部署和异构特性[1]。与传统同质网络相比,异构网络由宏基站、微基站、皮基站和飞基站等不同类型基站(Base Station,BS)组成,且各基站的发射功率、基站密度和数据传输速率均不同[2-3]。目前,随着移动设备数量的不断增加,由于上行链路异构网络的频谱共享策略,用户设备(User Equipment,UE)间的干扰逐渐加重[4]。因此,当前主流无线通信标准均已采用基于正交频分多址(Orthogonal Frequency Division Multiple Access,OFDMA)的异构网络[5]。另外,随着UE的增加,异构网络的上行干扰也将逐渐明显[6]。因此,为进一步提高网络系统传输性能和用户体验,开展用户关联和功率控制的协同优化是异构网络研究中的重要主题[7]。
针对异构网络中用户关联和功率控制问题,众多专家学者对此进行了大量研究。文献[8]通过研究主要用户和次要用户间的上行通信链路能量效率,提出了一种基于凸优化理论的迭代算法,能够有效提高用户间的网络通信平衡。文献[9]基于非合作博弈理论,通过计算异构网络系统的吞吐量,提出了一种适用于异构网络的联合BS关联和功率控制算法,通过对长期速率加权的最大化处理来平衡网络负载,并结合异构网络的功率控制,可有效处理异构网络延迟和上行链路用户的关联问题。但上述方法由于联合用户关联和功率控制具有非凸和非线性特性,难以获得全局最优解。同时,在实际应用中由于通信环境的不断变化,上述方法无法获取有效的网络信息[10]。
因此,针对时变动态环境研究人员提出了基于人工智能的控制策略,通过不断与环境互动、强化学习,解决长期决策的复杂计算问题。文献[11]通过使用Q学习算法,提出了一种基于传统单蜂窝网络结构的设备到设备(Device to Device,D2D)的联合信道分配和功率控制策略,可有效提高网络学习性能。文献[12]通过将Q学习和深度神经网络(Deep Neural Network,DNN)相结合构成深度Q学习网络(Deep Q-learning Network,DQN),提出了一种基于分布式用户关联算法的在线学习方法,能够有效优化异构网络的能量效率。文献[13]提出了一种基于DQN框架的用户关联和信道分配深度强化学习算法,通过DQN方法对卸载决策和计算资源分配进行了优化。但上述方法所考虑的网络行动空间相对较小,无法满足异构网络中联合用户关联和功率控制问题中大状态空间和大动作空间的需求,在实际运行中难以通过Q学习算法获得良好性能。
综上所述,上述研究主要集中于异构网络中的联合用户群体和渠道分配问题,尚未考虑能量效率的综合分析。目前,随着各种新业务和应用场景的不断涌现,UE的能耗也随着密集型移动数据计算和应用程序的增长而上升,但当前的电池技术无法满足移动UE的能源消耗。因此,异构网络中UE的能量效率优化变得更加重要。基于以上分析,本文提出了一种多智能体DQN方法,对上行链路中的用户关联和功率控制进行优化处理,并基于能量消耗与UE电池容量的相互作用,将UE的能量效率重新定义为奖励函数,实现对所有UE能量效率的最大化。仿真实验验证了所提算法的正确性和有效性。
1 系统模型构建
图1所示为典型的异构网络结构图[14]。其中,在宏BS的覆盖区域内,部署了一组小型BS,在不失一般性的情况下,将所有BS的集合表示为M={0,1,2,…,m}。
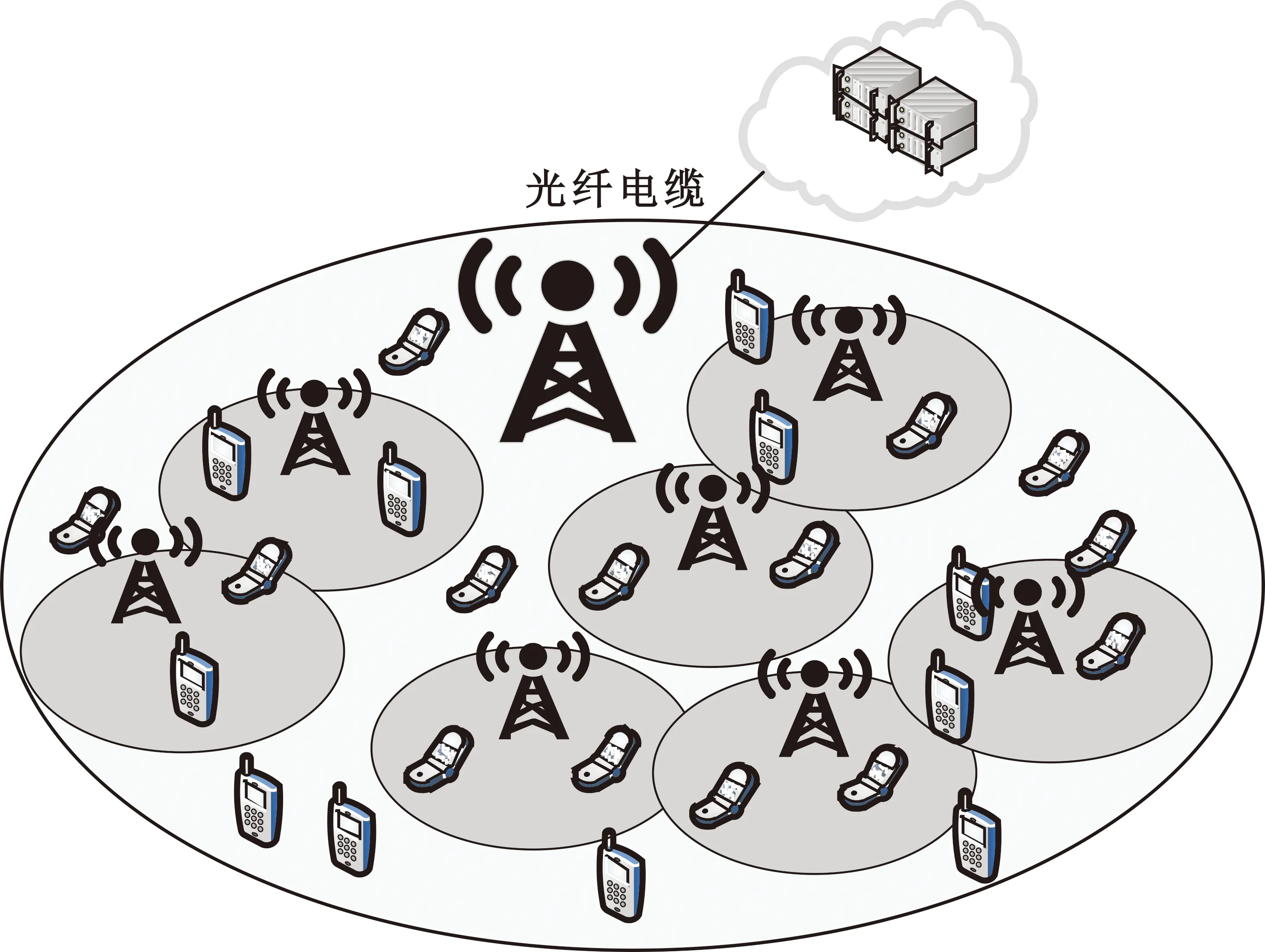
图1 典型的异构网络
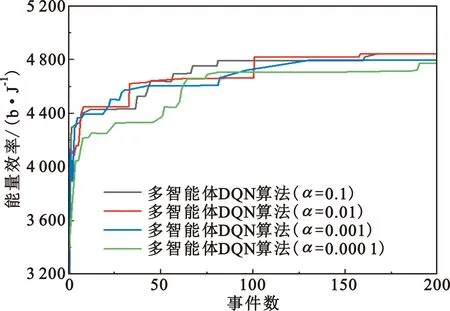
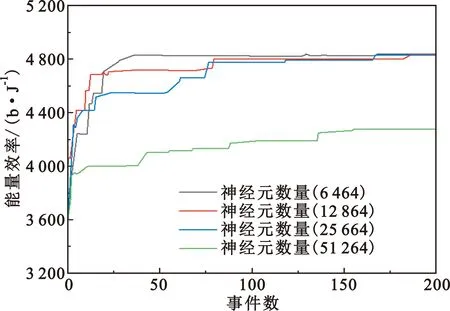
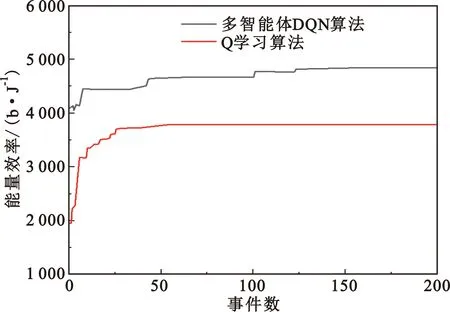
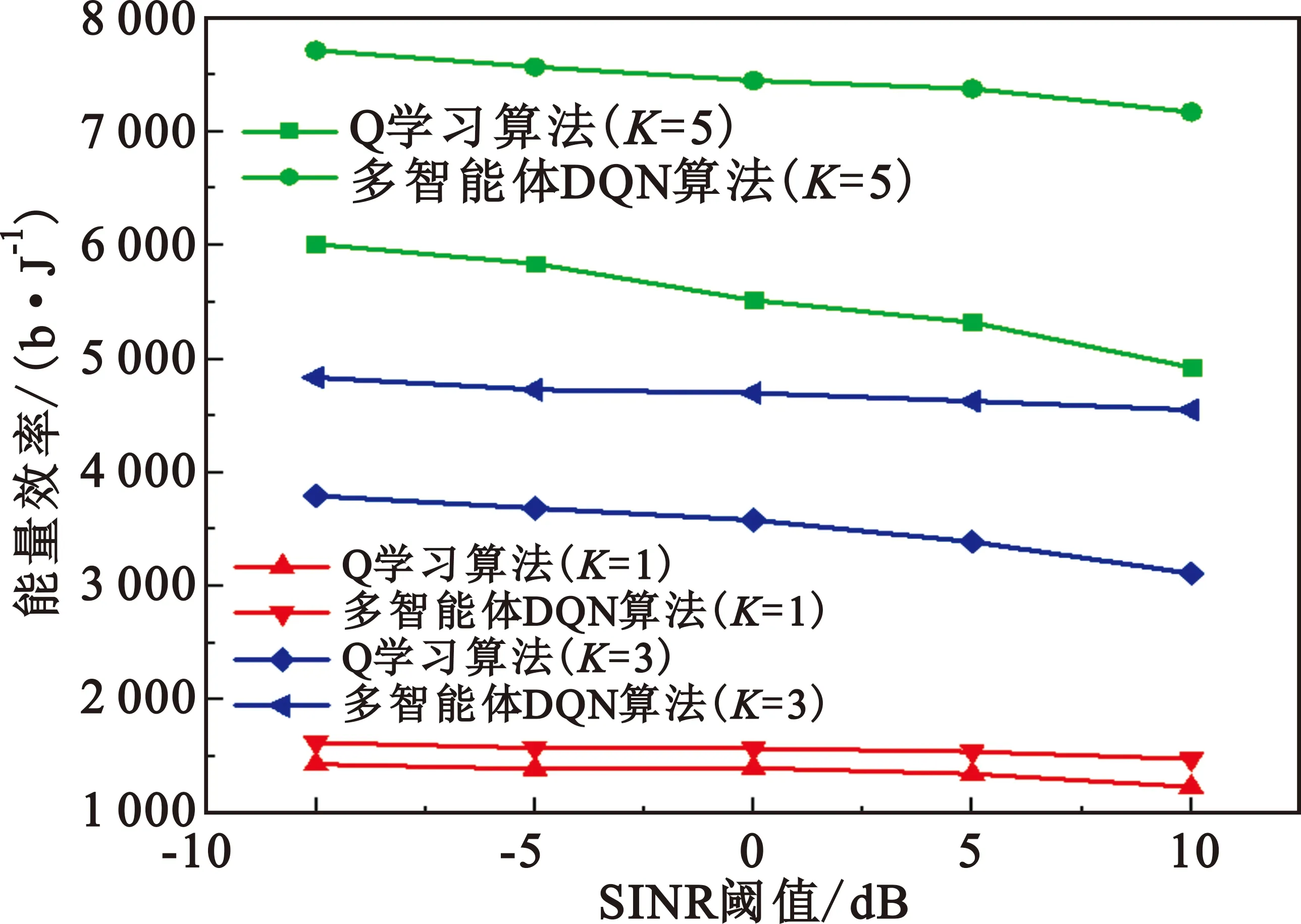
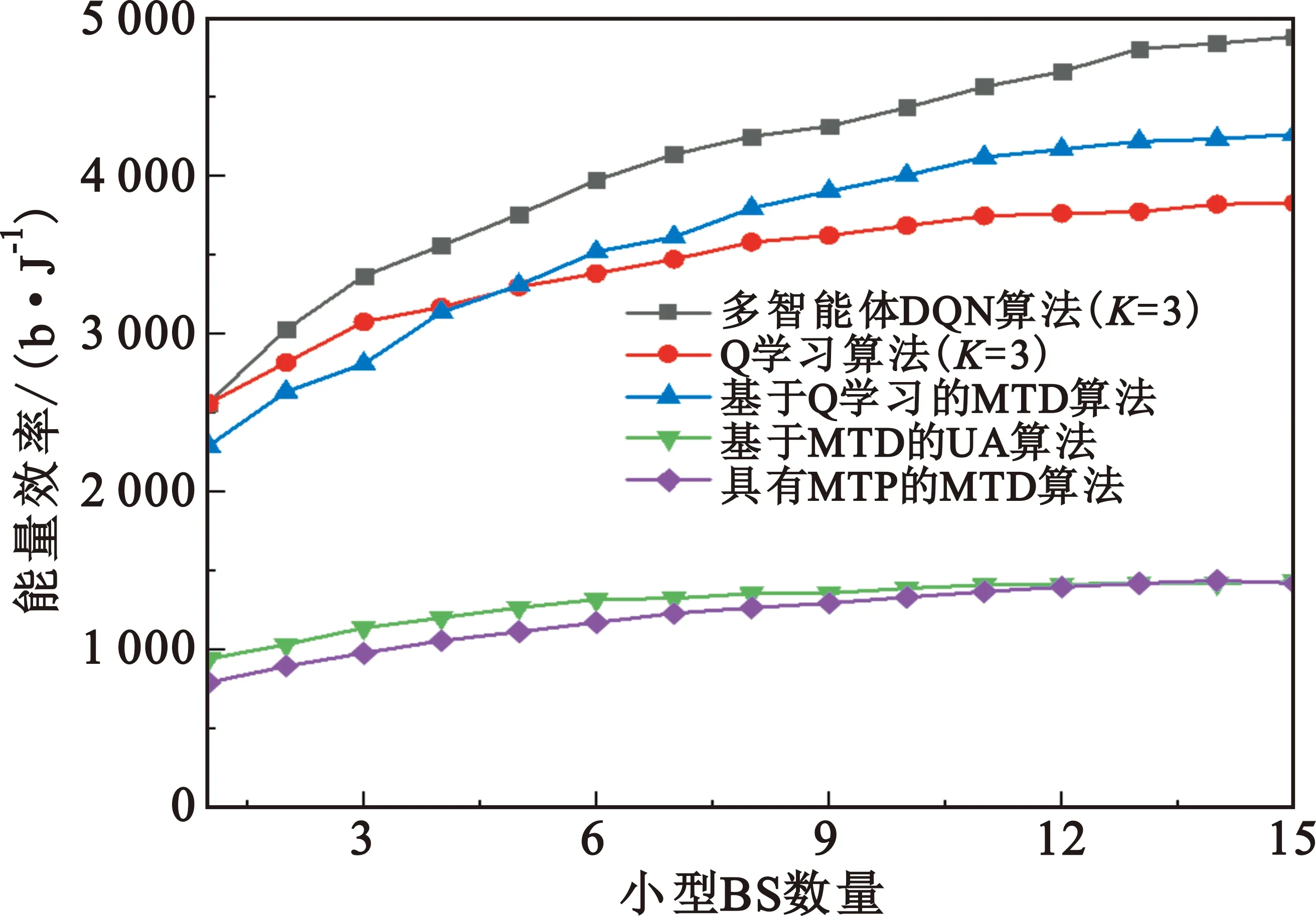
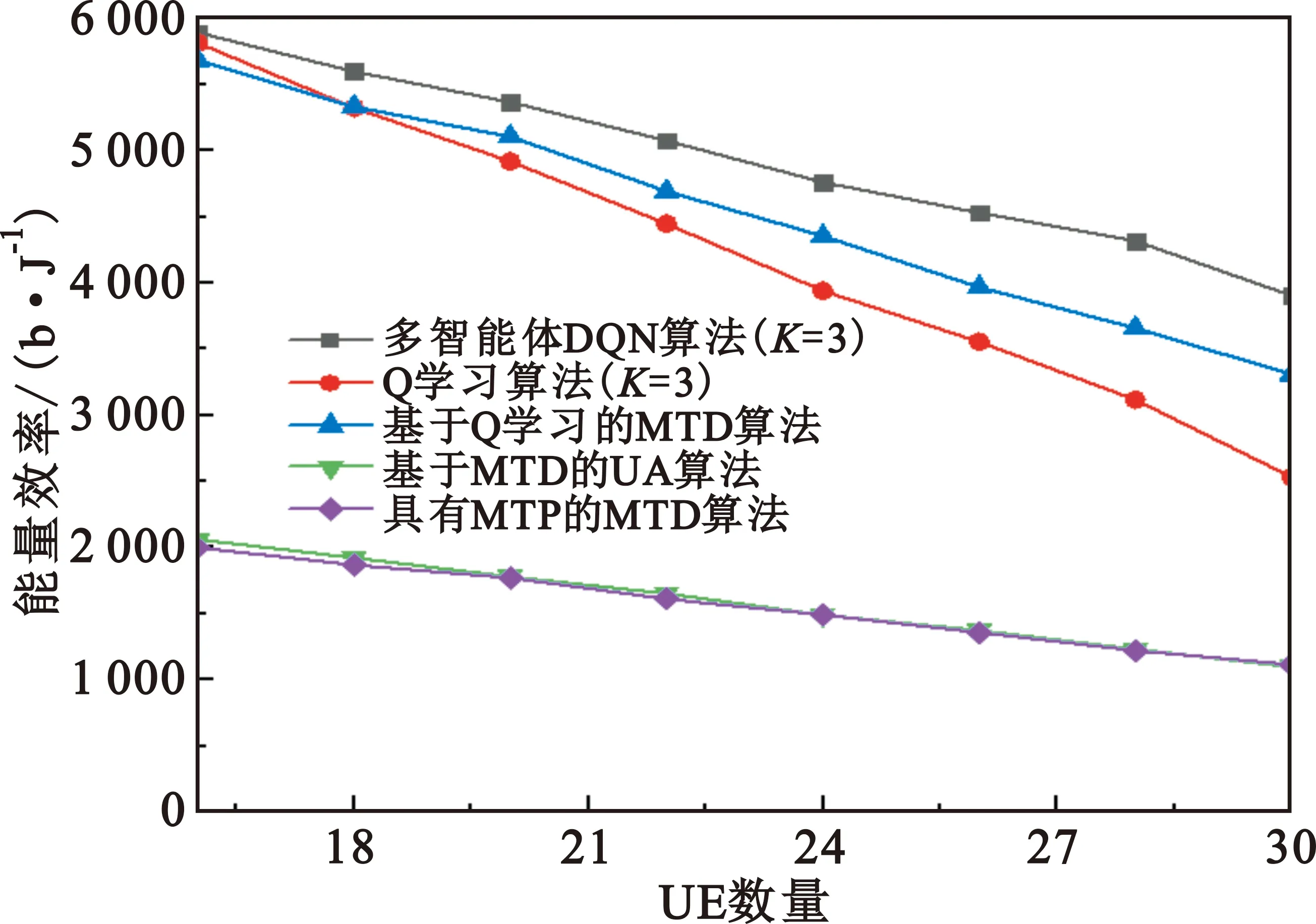
该模型的学习过程由云服务器完成,云服务器通过光纤电缆与宏BS或小型BS进行连接。UE随机分布在网络中,且UE的集合为U={1,2,…,u},其中u为UE的总数。通常,基于OFDMA的异构网络系统具有n个子信道,分别表示为N={1,2,…,n},n 假设所有BS和UE均配备有独立天线,信道增益主要受瑞利衰落gu,m、对数正态阴影LS和路径损耗的影响,则将宏BS和小型BS的路径损耗分别建模为PL1和PL2。因此,具有第m个BS的第n个子信道上的第n个用户的信道增益的数学表达式如式(1)所示: (1) 为详细阐明UE与BS间的关系,定义了一组整数二进制变量au,m来表示BS与UE间链路的有效性,其数学表达式如式(2)所示: (2) 此外,UE的功耗由静态功耗和动态功耗两部分组成。其中,静态功耗是运行电路组件如转换器、混频器、滤波器等时消耗功率,而动态功耗被视为发射功耗。由于数字手机中的发射功率只能在离散水平上进行更新,因此实际应用中可以通过有限数量的值对发射功率进行设置。 (3) 因此,在第n个子信道上连接到第m个BS的第u个UE的信号干扰加噪声比(Signal-to-Interference plus Noise Ratio,SINR)如式(4)所示[15]: (4) 根据香农公式,第u个UE的数据速率如式(5)所示: (5) 由此,在本文的系统模型中,结合用户关联和功率控制,提出了使异构网络中所有UE的能量效率最大化的优化问题。将所有UE的能量效率定义为每个UE的能量效率之和,并将用户在第n个子信道上选择第m个BS的个人能效,定义为可实现的吞吐量与用户的总功耗的比值,如式(6)所示: (6) 因此,本文异构网络模型的总能效最大化问题可以表述为式(7)所示: C3:au,m∈{0,1}, (7) 式中:A表示用户关联矩阵,p表示所有UE的发射功率向量,γth为预定义的最小干扰加噪声比;约束C1表示每个UE的发射功率与给定的最大发射功率的比值,C2可确保满足每个UE的QoS要求,C3与C4能够确保每个UE只能与一个BS相关联。因此,通过解决混合整数非线性规划问题P1,可以找到关于UE与BS的关联以及传输功率,即A和p的最优控制策略。 从式(7)可知,用户关联和功率控制机制是相互关联的。为有效解决异构网络的混合整数和非凸性问题,以奖励函数为基础提出了基于强化学习的马尔科夫决策过程。 在本文研究的场景中,主要是将协同优化问题P1转换为马尔科夫决策过程(S,A,R,Pss′)。其中,S为决策过程状态空间,A为UE的动作空间,R为奖励函数,Pss′为从状态s过渡到状态s′的概率。随后,基于马尔科夫决策过程,构建强化学习过程的系统状态空间、动作空间和奖励函数,具体如下: (1)状态空间 在公式化问题P1中,智能体UE需选择BS进行通信,确定发射功率,并将系统状态空间定义为sstate={s1,s2,…,sj,…,s(M×K)U}。其中,sj=j表示所有UE与BS和功率控制相关联的状态。根据系统状态空间公式可知,随着U的逐渐增加,状态数量呈指数增长。此外,由于每个UE仅可选择一个子信道,选择相同子信道的用户将产生相互干扰。因此,从子信道角度出发,每个子信道的状态空间可定义为sn={s1,s2,…,sj,…,s(M×K)Nn},其中Nn为第n个子信道服务中UE的数量。 (2)行动空间 在公式化问题P1中,需要控制UE与BS的关联和发射功率,否则UE在时刻t的第n个子信道中的动作将出现发散。因此,对于第n个子通道中的所有动作,可定义时刻t的动作空间为an(t)={a1(t),a2(t),…,aj(t),…,a(M×N)Nn(t)}。系统N个子通道的所有动作如式(8)所示: a(t)={a1(t),a2(t),…,an(t),…,aN(t)}。 (8) (3)奖励函数 通常,学习过程由强化学习框架中的奖励函数驱动,在基于OFDMA的异构网络下,将所有UE的总能量效率定义为系统奖励函数,其数学表达式如式(9)所示: (9) 式中:rn(t)为第n个子通道的奖励函数,通过与环境的相互作用最大化进行最优策略学习。 通过以上分析,可以将问题P1转换为问题P2,其数学表达式如式(10)所示: (10) (11) 式中:γ∈[0,1]为折现因子,T为最大事件数。其中,当γ=0时,返回的奖励为当前奖励;当γ=1时,Rn(τ)等于奖励的总和。 (12) (13) 因此,基于Bellman方程,异构网络的最佳Q值函数如式(14)所示: (14) (15) 对式(14)和式(15)进行联合求解,其结果如式(16)所示: (16) (17) 式中:α为学习率。 由于Q学习方法需选择具有最佳值的动作,且对所选动作进行评估。另外,Q学习方法使用采样方法进行状态选择,将使得采样状态过高,且采样状态和未采样状态之间的差距将会逐渐增大。通常,异构网络的状态和动作空间较大,使用Q学习方法获得的最优解往往存在不足,即Q学习方法无法为大规模系统状态空间采样某些特殊状态。因此,为了应对大规模的系统状态空间问题,须采用深度强化学习方法。 (18) 由于数据样本之间存在差异,系统难以获得一个平滑的学习模型。因此,考虑具有权重参数θ的目标网络作为系统智能体。通常,多智能体DQN方法有行为网络和目标网络两种,通过使用目标网络,计算目标值yi的学习模型,在一定时间内能够保持权重参数恒定不变,减轻学习模型的波动性。此外,也可通过行为网络获得系统效率的估值。 通常,在强化学习过程中,经过一定数量的迭代之后,行为网络的权重参数θ将与目标网络同步,即θ→θ-。随后,自动进入下一阶段的学习。对于行为网络,智能体将使用ε贪婪策略选择动作an(τ),并使用最小损失函数为每次迭代更新的参数θ,其数学表达如式(19)所示: L(θ)=∑[(yj-Qπ(sn,an|θ))2] , (19) (20) DQN方法中,由于数据样本之间的相关性,将导致学习不稳定。因此,可运用经验回放技术进行DQN学习,其中主要包含存储数据和采样数据两部分,经验数据按迭代顺序存储到回放存储器D中。在DQN学习过程中,智能体将选择动作an(τ),获得奖励rn(τ)并转到下一个状态。随后,将向量存储到体验存储器中。如果内存D的存储已满,则新的体验数据将覆盖前一次迭代生成的数据。图2所示为多智能体DQN策略图,其中状态空间和行为空间通过回放存储器进行关联。 图2 多智能体DQN策略图 在初始运行过程中,每个智能体分别为行为网络和目标网络的初始化内存D,以及权重参数的θ和θ-。随后,智能体初始化开始进入状态,并使用ε贪婪策略选择动作an(τ)。最后,如果状态约束条件满足,则智能体将发送有关用户关联的信息,并将功率发送到环境条件中,通过奖励函数rn(τ)和下一状态获得功率比值n;否则,智能体将不会回放任何内容。 向量Sn主要存储在回放存储器D中,通过将样本随机小批量写入存储器D,可通过初始化更新行为网络的权重参数。当训练一定数量的迭代次数时,行为网络的参数将同步到目标网络,并开始下一阶段的学习。 选取具有一个宏BS和小型BS的两层异构网络进行多智能体DQN算法仿真实验。其中,令25个UE随机分散在宏BS的覆盖范围内,并设置其区间为200 m×200 m。此外,令小型BS也随机分布在相关区域中。 其中,UE的最大发射功率为23 dBm,子信道总数为15,宏BS和小型BS的传输损耗为PL1=34+40 lg(d),PL2=37+30lg(d)。其中,d是从BS到UE的距离,对数法线阴影为8 dB,噪声功率设置为σ2={-174 dBm}。 为估计Q函数计算结果,采用DNN算法在包含64个神经元的全连接神经网络的两个隐藏层以及一个输出层模型中进行计算,表1所示为DQN的详细参数。 表1 DQN详细参数 首先,对具有不同学习参数,如学习率和神经元数量的DNN的性能进行仿真,分析具有不同学习率的训练效率,其仿真结果如图3所示。由图3可知,随着事件数的增加,所有UE的能量效率逐渐收敛。此外,随着学习率α的变化,相较于α=0.1、α=0.001、α=0.000 1,当α=0.01时,所有UE的能效性能最佳。对α=0.01和α=0.1两种情况进行比较分析可知,当学习率α较大时,算法计算结果难以达到最佳值;当学习率相对较小时,将可能导致局部最优。因此,考虑到算法的实际执行,将所提算法的学习率α设置为0.01。 图3 不同学习率下的能量效率 图4所示为DNN结构中不同数量神经元的性能。由图4可知,随着神经元数量的不断增加,所有UE的能量效率都逐渐下降。由于数据样本的稀疏性,当神经元数量过多时,优化问题可能会导致过度拟合,并增加更多的训练时间。当神经元等于第一层的64和256时,两条曲线的收敛性几乎相同,而其他情况在收敛性上的表现则较差。因此,将两个隐藏层的神经元均设置为64。 图4 DNN结构的能量效率与神经元数目的关系 在SINR设置为γ=-10 dB的情况下,对多智能体DQN算法的收敛性能进行分析,并将其与经典Q学习框架进行对比分析。图5所示为对比分析收敛性结果图,由图可知,Q学习的系统能效低于使用多智能体的DQN方法;且随着事件数的增加,两种方案的能量效率均会逐渐增加并趋于收敛,但多智能体DQN算法在学习速度上优于Q学习方法。对于Q学习方法及多智能体DQN算法,当事件数约等于180时,其系统能量效率改善较低;当事件约等于157时,其系统能量效率趋于稳定。由此可知,多智能体DQN算法虽开始呈现出发散性,但随着事件数的增加,其不稳定程度会逐渐降低,并最终趋于收敛。因为智能体随机选择并将信息存储到回放内存中,经过多次迭代,多智能体DQN算法开始从经验中学习,从而提升其稳定程度。 图5 收敛性能 此外,在不同SINR阈值下采用Q学习算法和多智能体DQN算法时,模拟所有UE的能量效率。图6所示为不同K值下能量效率与SINR阈值的关系图,由图可知,随着UE中SINR阈值的增加,所有UE的能量效率均逐渐降低。因为要实现较高的SINR,必然会消耗更多的功率,这将降低所有UE的能效。另外,随着功率水平的增加,所有UE的能量效率也随之提高。因为随着功率水平的增加,智能体可以在固定的用户关联下选择更合适的传输功率,从而提高能量效率。对于K=1的情况,UE的发射功率等于最大发射功率,即PMAX=23 dB。根据图6可知,当UE的发射功率最大时,其能量效率最差。 图6 不同K值下能量效率与SINR阈值的关系 此外,本文对不同数量小型BS的所有用户设备的能量效率展开了仿真研究。设置γ=-10 dB,K=3,仿真结果如图7所示。为了评估多智能体DQN算法的性能,除Q学习算法外,本文还选取了其他三种算法进行对比研究,即基于Q学习的MTD算法、基于信息传递部分(Message Transfer Part,MTP)的UA算法,以及具有MTP的动目标检测(Moving Target Detection,MTD)算法。 图7 能量效率与小型基站数量的关系 对于具有基于Q学习的MTD方案,用户选择最小传输距离用户关联方案,并采用基于Q学习的功率控制算法。对于具有MTP方案的UA,用户采用基于Q学习的用户关联方案,并使用其最大发送功率进行发送。最后,对于带有MTP方案的MTD,用户选择最小传输距离用户关联方案,并使用其最大发射功率进行发射。由仿真结果可知,随着小型BS数量的增加,所有UE的能效将呈现出先增加,然后逐渐降低的现象。 对于基于Q学习的MTD算法,当小型BS的数量较少时,Q学习算法的性能表现更好。随着小型BS数量的增加,Q学习算法的性能将逐渐下降。主要是由于状态和动作的空间变大,部分状态被高估,并且没有被采样。因此,在基于OFDMA的异构网络模型中,小型BS的数量设计至关重要。 图8所示为不同数量的UE下的所有UE的能量效率图。由图可知,相较于其他四种方案,多智能体DQN算法在所有UE的能量效率中均获得了最佳性能。这是因为与基于Q学习的MTD算法、基于MTP的UA算法,以及具有MTP的MTD算法相比,多智能体DQN算法不仅优化了用户关联,还对发射功率进行了优化。通过使用DNN,多智能体DQN算法可以克服Q学习算法的缺点。因此,与Q学习算法相比,多智能体DQN算法具有更加优越的性能。这是因为系统状态和动作空间将随着UE数量的增加而增加。另外,随着UE数量的逐渐增加,所有方案的UE能效性能均会逐渐下降,是因为越高的用户数量将会引起越严重的干扰。 图8 能量效率与用户数量的关系 本文针对基于OFDMA异构网络中的用户关联和功率控制协同优化问题,提出了一种多智能体DQN方法,通过仿真计算和分析得出以下结论: (1)相较于传统的优化算法,多智能体DQN算法所需要的通信信息更少,计算时间更短,优化效率更高; (2)相较于传统的Q学习算法,多智能体DQN算法具有更好的收敛性能; (3)所提方法能够有效提升UE的服务质量与能效,并可获得最大的长期总体网络实用性。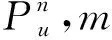
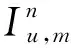
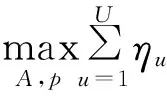

2 DQN强化学习过程构建
2.1 马尔科夫决策转换
2.2 强化学习
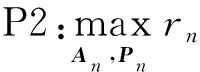
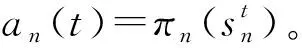
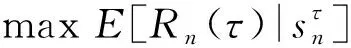
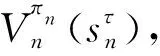
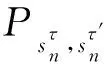
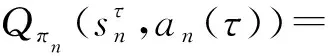
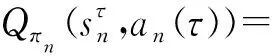
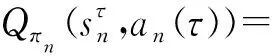
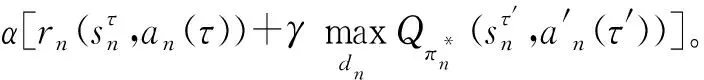
3 多智能体DQN框架
3.1 多智能体DQN方法
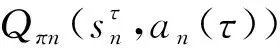
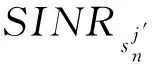
3.2 多智能体DQN模型构建

4 仿真结果与分析
4.1 仿真计算

4.2 能量效率仿真
5 结 论

