基于负荷预测的区域供暖系统控制模型研究
李晋芝 何大四 姜俞龙 李静
中原工学院能源与环境学院
随着建筑业的迅猛发展,近年来建筑能耗在社会总能耗中所占的比例已经达到了27.45%以上[1],其中北方城镇的采暖能耗所占比重更是高达36%。但目前在我国供暖季过量供热的问题比较严重,导致我国建筑的实际供热消耗量超出建筑平均需热量的35%左右,且建筑能耗是同纬度下北欧一些国家的2~4 倍[2]。针对热量供需不匹配的现象,陈路路[3]利用Simulink软件对供暖系统进行分环节建模研究系统达到稳定时的时间延迟,但整个系统在室外温度不变且无调节工况下运行,没有探究不同调节方案下系统的动态响应情况。为了更好地指导供暖系统节能高效运行,国内外众多学者都对热负荷预测做出了相关研究,李思琦[4]等人提出经差分进化算法优化后的BP 神经网络对供热负荷建立预测模型的方法,张佼[5]通过分析影响支持向量回归机性能表现的参数,提出了基于遗传算法优化的SVR 供热负荷预测模型,Martinaitis 等人结合室外气象参数和末端用户热需求,通过热负荷预测对换热站供热量进行调控[6,7],除此之外还有状态估计法、时间序列法等,均可以达到预测的精度,但机理、编程复杂,没有在供暖自控系统中得到普遍应用。因此非常有必要利用计算机仿真技术对不同调节方案下的供暖系统动态特性进行研究,加紧从传统的粗放式调节模式向精益化的调节模式转变,从传统的静态调节转变为动态的适应性调节,最终降低供暖能耗,提高能源效率。
1 系统数学模型
以直接连接的区域供暖系统为例,将整个系统分为热源、热网、散热器和建筑区域四部分,以四个部分的质量和能量守恒方程为基础,利用热容量质点系法建立各部分的数学模型。
1.1 锅炉模型
忽略掉锅炉向外界的散热,依据锅炉内容纳的热水储热量等于通过燃料燃烧供给锅炉的净热量减去加热补给水与热网循环水所需热量建立数学模型如式(1)、(2)所示:
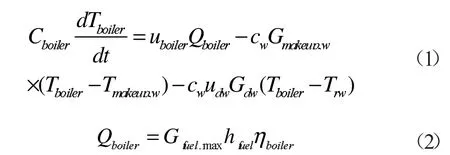
式中:C 为热容量;T 为温度;u 为控制参数;Q 为设计热负荷;Gfuel,max为锅炉额定消耗燃料速率;hfuel为燃料热值;η 为热效率;cw为水的比热容;G 为流量;下角标boiler 表示锅炉,makeup 表示补给水,dw 表示热网,r表示回水。
1.2 热网模型
假设管道和保温材质均匀,忽略保温层蓄热,依据存储在n 管段中的热量等于上游管段传送热量减去n 管段的散热损失和泄漏损失这一关系建立数学模型如式(3):

式中:L 为管段长度;K 为管段散热系数;下角标n 表示管段编号,leak 表示泄漏损失,soil 表示土壤。
1.3 散热器模型
忽略散热器管壁的蓄热及流体的轴向蓄热,依据供暖管网供给散热器的热量减去散热器供给房间的热量等于散热器内热水获得的净热量建立数学模型如式(4)[8]:

式中:q 为散热量;下角标heater 表示散热器。
1.4 建筑区域模型
1.4.1 围护结构模型
本文模拟的工程物理模型为四栋居民楼,供暖面积共计74880 m2。在对围护结构进行建模研究时,先将每栋建筑内的空气视为一个温度节点,然后分别对地面、屋顶、墙体进行划分,建立不同材料层的动态平衡方程式及对应仿真模块,最后综合考虑建筑向室外的散热、冷风渗透热损失,得到建筑围护结构耗热量计算方程式(5):
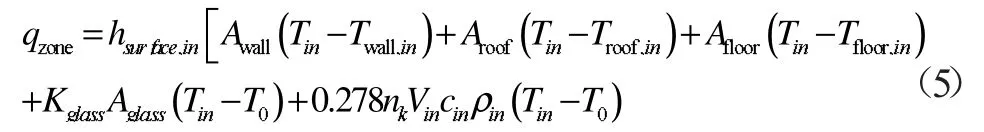
式中:A 为面积,h 为对流换热系数,ρ 为密度,nk为换气次数,V 为体积;下角标zone 表示仿真区域,wall、roof、floor 分别表示外墙、屋顶和地面,in 表示室内空气,out 或0 表示室外空气,glass 表示玻璃,solar 表示太阳辐射。
1.4.2 室内温度模型
依据散热器提供的热量加上通过外窗获得的太阳辐射热量减去围护结构耗热量等于室内空气蓄热量这一等式关系建立室内温度数学模型如式(6),其中下角标z 表示仿真区域:

1.5 仿真模型建立
在MATLAB/Simulink 软件环境下建立上述各部分数学模型对应的仿真模块,基于实际工程物理模型将各模块进行组合与连接,得到整个区域供暖系统的仿真模型如图1 所示:

图1 区域供暖系统仿真模型
2 调节控制模型
2.1 无调节模型
为了更好地对比直接连接供暖系统中常规调节方式与基于预测方法调节对系统运行指导过程中的能源消耗量,首先建立定流量定供水温度运行方案下的供暖系统仿真模型,即控制燃气消耗量和相对流量的参数uboiler、udw均为定值,以此为基础,将下述两种调节方案模型的能耗进行对比。
2.2 室外温度补偿调节模型
根据室外空气温度来调节热源处供水温度是区域供暖系统热源处现在常用的供热量控制方法。采用分阶段改变流量的质调节方式,以室外温度-5 ℃时为分界线将循环水流量分为100%和80%两个阶段,供回水温度与室外温度条件的对应关系如图2 所示:

图2 锅炉房运行温度曲线图
2.3 基于负荷预测的调节模型
本节主要引入结合了未来4 小时,前24 小时以及前25 到48 小时内三个时间段平均温度的综合室外温度tw,i,e,基于最小二乘法得到建筑热负荷与综合室外温度的线性关系[9],利用数据挖掘得到的结果提前调节运行参数,旨在得出适合工程实际应用简便易操作的运行调节方案。最终得到综合室外温度和预测供热负荷表达式为:
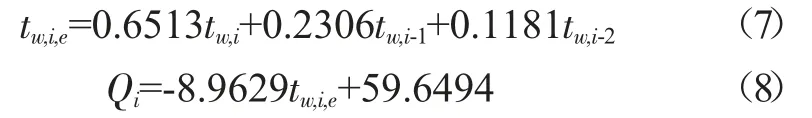
式中:tw,i-n为三个时间段对应的平均温度,Qi为预测负荷。在运行调节中,把室内供暖设计温度代入式(8)中便可得到设计供暖热负荷Q',预测负荷与设计负荷之比即为相对热负荷比,且满足等式(9):
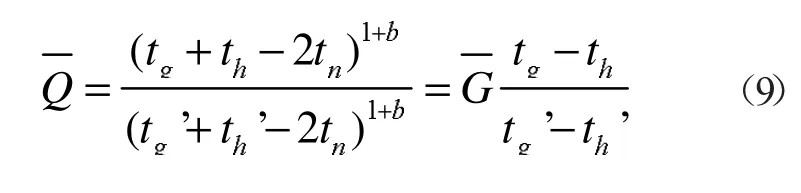
最后选择使用一种修正的质量综合调节方式[10],即在热负荷较大时为量调节,热负荷较小时为质调节,结合上式及调节策略可以得到热网运行调节曲线如图3,在调节过程中,根据计算出的负荷比对未来四小时的供热参数进行预测,就可以提前做出调节动作,从而抵消掉由于系统的大滞后和延迟带来的供需不匹配的问题。

图3 质量综合调节曲线
3 仿真结果与分析
运行各调节方案下的仿真模块,观察室内温度波动情况对比如图4:


图4 三种调节方案下的室内温度响应情况
观察可得,在负荷预测模块提前对供暖系统做出指导调节动作的前提下,室内温度响应曲线波动范围缩小到了20±1 ℃,相较于常规调节方式,距离室内设计温度的上下浮动值减小了1.5 ℃,极大改善了控制效果。
假设水力工况平衡,则说明利用改进后的质量-流量调节方式所建立的供热负荷预测模型对区域供暖系统进行控制的效果是比较理想的。为了进一步探究此方案的节能性,建立锅炉燃料消耗量计算模块和管网循环水泵耗电量计算模块,观察供暖季运行过程中的能耗变化情况如图5 所示:

图5 供暖季能耗对比情况
由整个供暖季内锅炉和水泵的能耗统计对比图可以看出,方案三中锅炉的总耗气量和水泵的耗电量变化均比较大,将三个方案供暖季的总能耗进行计算,折算成标准煤进行比较结果如表1 所示:
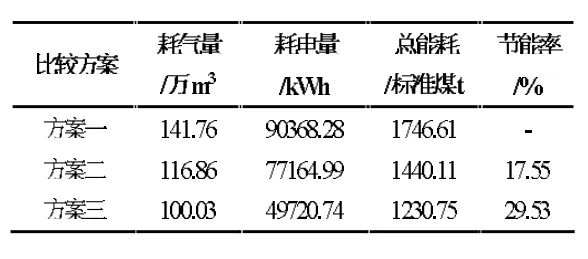
表1 整个供暖季能耗模拟结果
通过计算结果可知,采用基于负荷预测调节方式整个供暖季的总能耗为1230.75t 标准煤,相比方案一节能率为29.53%,相比于方案二节能率为14.54%。
4 结语
本文引入基于数据挖掘机理的供热负荷预测方法简单,且经模拟发现可以达到较为理想的调节效果。基于建立的整个供暖系统仿真模型,代入不同调节方案运行后得出,整个供暖季中本所采用的负荷预测调节方式相较于定流量定供水温度调节方式节能率可达29.53%,相较于常规调节方式节能率可达14.54%。

