基于规则分组的DFA正则表达式匹配算法
朱 俊
(1.合肥工业大学计算机与信息学院,合肥 230009;2.安徽水利水电职业技术学院电子信息工程学院,合肥 231603)
入侵检测系统(Intrusion Detection Systems,IDS)不仅能够识别出网络中的入侵行为,还能检测出网络中的漏洞信息,从而采取相应对策进行处理和防范,阻止入侵行为带来的危害.入侵检测方法主要分为异常检测和误用检测两大类.异常检测主要采用统计分析的方法,常用的有:神经网络、人工免疫、统计模型、数据挖掘等[1].误用检测主要采用模式匹配的方法,模式匹配技术的过程通常是提前将特征信息提取出来,存放到模式库中,再把收集到的数据与模式库中的特征信息进行比对,从而发现入侵行为.当今,模式匹配技术是入侵检测系统主要采用的方式.随着计算机网络技术的飞速发展,网络带宽的使用量增长迅速,单位时间传输的数据呈几何倍数增加,规则数量随之增加,所带来的最大问题是如何快速地进行检测.构建有限自动机对于模式匹配来说非常有效.构建有限自动机后,对每个文本字符只需要进行一次遍历,因而在时间复杂度上有很大的优势,构建有限自动机所花费的时间复杂度通常为O(n)[1-2].但是,在输入字符集元素很庞大的情况下,建立有限自动机所花费的时间就会大大地增加.
为了充分发挥确定性有限自动机(deterministic finite automata,DFA)速度快的优势,对其存储空间的算法进行优化具有重要意义.如果有多条正则表达式构造成一个DFA,则各个规则会有相同或相似情况,状态集合很大,导致出现状态爆炸问题[2-4].Yu Fang 等[5]提出了对规则进行分组的算法,来解决状态爆炸问题,这种分组算法可以在一定程度上抑制状态爆炸问题,但在存储空间上并未有大的提升,并且当分组数量大时,算法空间复杂度较大.
1 正则表达式
1.1 问题描述
传统的入侵检测主要使用朴素模式匹配算法或一些经典匹配算法,如AC 算法、BM 算法、KMP算法等[1],但是这些算法的缺点是描述精确字符串的能力非常有限.随着计算机技术的发展,入侵行为变得多样,特征更加复杂,增加了代码复杂度.简单的字符串匹配不再满足入侵检测需求.
正则表达式起源于科学家用一种数学方法来描述神经网络的研究,后来正则表达式被用于计算机领域,先后在Unix 的编辑器qed 和ed 以及grep 中得到应用,著名的Perl 语言也使用正则表达式.近年来,在WINDOWS 环境下,正则表达式也得到了广泛的应用.主流的开发语言delphi、PHP、C#、Java、C++、VB、Javascript、Ruby 以及Python 等都可以支持正则表达式.
正则表达式非常灵活、逻辑性强、功能强大,通过简单的方式就可以对字符串进行操作.正则表达式应用的对象通常是文本,所以适用范围很广,一些普通的文本编辑器都可以使用,如EditPlus 等.正因为正则表达式的优势,比精确字符串匹配更适合进行深度报文检测,更符合入侵检测场景应用.像开源的入侵检测系统Snort 基本上都使用正则表达式来对规则进行描述.一些网络安全设备也使用正则表达式来检测,判断是否有入侵行为[2-4].
1.2 状态爆炸
状态爆炸是指将多个正则表达式生成一个DFA 时的状态总数比其独自生成DFA 时的状态总数量更大.例如正则表达式E1 和E2,E1 生成的DFA 的状态数量为Count(E1),E2 生成的DFA 的状态数量为Count(E2),将E1 和E2 合并后的表达式为E12,生成的DFA 的状态数量为Count(E12),如果存在Count(E1)+Count(E2) 图1 正则表达式E1的DFA 图2 正则表达式E2的DFA 判断正则表达式集合分组是否有效,主要看生成DFA 的状态总数及分组的数量. (1)DFA 状态总数越多,所需要的存储空间也越大.所以,减少DFA 状态总数,可以减小所需要的存储空间,在空间复杂度上得到一定的优化. (2)分组的总数量会影响到DFA 的匹配速度,当对某个字符的状态转移表进行访问时,分组数越多,访问的次数相应会越多,匹配的效率就会低,分组数越少,访问的次数相应减少,匹配的效率就会提高. 在一般情况下,分组数量越多,DFA 状态总数量就会越小,分组数量越少,DFA 状态总数量就会越大,只有当DFA 状态总数和分组的总数量这两个因素在一个合适的结合点时,达到存储空间和匹配速度上总体最优化. 通常一个有限自动机包括五个元素,例如有限自动机M(Q,q0,A,ε,δ),其中:Q 表示状态的有限集合,q0∈Q代表初始状态,A 是一个接受状态集合且A⊆Q,ε是有限的输入字符表,包含256 个字符,δ 是M 的转移函数,为Q×ε到Q 的函数[1]. 有限自动机从初始状态q0开始,如果有限自动机在状态q时读入了输入字符a,则它从状态q变为状态δ(q,a).每当其当前状态q属于A时,就说明自动机M接受了迄今为止所输入的字符串.没有被接收的输入称为拒绝的输入. 有限自动机M可以推导出一个函数,称为终态函数Φ,M接受字符串w,当且仅当Φ(w)∈A.函数Φ由下列递归关系定义: 对于任意一个模式P,都可以构造一个字符串匹配自动机,在预处理阶段,先根据模式P构造出DFA,然后利用构造出的DFA 来遍历字符串,首先定义一个辅助函数σ,称为相应P的后缀函数.函数σ是一个从ε*到{0,1,…,m}上定义的映射,是x的后缀P的最长前缀的长度: 因为空字符串P0=ε是每一个字符串的后缀,所以后缀函数是有完备定义的.例如,对模式P=ab,有σ(ε)=0,σ(ccaca)=1,σ(ccab)=2.对一个长度为m的模式P来说,σ(x)=m,当且仅当P⊃x.根据后缀函数的定义有:如果x⊃y,则σ(x)≤σ(y)[1]. 已知模式P[1,…,m],其对应的字符串匹配自动机定义如下: 状态集Q为{0,1,…,m},初始状态q0为0,状态m是唯一的接受状态. 对任意状态q和字符a,变迁函数δ由如下等式定义. 自动机的操作中保持如下条件不变: 这意味着对文本字符串T的前面i个字符进行扫描后,自动机的状态为Φ(Ti)=q,其中q=σ(Ti)是最长后缀Ti的长度,Ti是模式P的一个前缀.如果下面扫描到的字符为T[i+1]=a,则自动机的状态应转换为σ(Ti+1)=σ(Tia).也就是说,为了计算P的前缀Tia的最长后缀的长度,可以先计算出P的前缀Pqa的最长后缀.在每一种状态上,自动机仅需要知道迄今已读入的字符串的后缀P的最长前缀的长度. 对于长度为m的模式的任意字符串匹配自动机来说,状态集Q为{0,1,…,m},初始状态为唯一的接收态是状态m[1]. 从FAM 算法可以看出,如果一个长度为n的文本字符串,计算其所需要的匹配时间,如果不包括计算转换函数δ所需要的预处理时间,那么它的时间复杂度为O(n). 下列过程根据一个给定模式P[1,…,n]来计算转换函数φ[1]. DFA 适用在不要求回溯的线性状态,它的一个显著特点是在匹配很长的字符串时依然能够确保成功. 基于规则优先级的匹配算法的出发点是减少DFA 中出现的爆炸问题,同时在时间复杂度上和空间复杂度两个维度上占用较少的消耗. 图1 和图2 描述了当用一个正则表达式构造DFA 时,会导致状态爆炸的情况.在另外一些情况下,虽然一条规则不会引起状态爆炸,但当多个正则表达式构造同一个DFA 时,由于其相互作用影响,也会造成状态爆炸.极端情况下,如果每个正则表达式中出现x次同一字符串,则复杂度为O((x+1)y).文献[2-3,5-6]中提出了对正则表达式进行分组,从而减少状态爆炸情况的思想.其主要思想是通过找到正则表达式中的等价因子,然后构造出关系图,每个正则表达式作为关系图中的顶点,如果任两个正则表达式存在造价因子,则将该两顶点连接起来.在进行分组前,找出一个与其他表达式相关度最少的一个正则表达式,然后将该正则表达式加入分组里,接下来重复上述步骤,将其他的正则表达式依次加入分组里,当这个分组的DFA 的存储空间达到一定的阈值时,将新建一个分组,接下来继续重复上述步骤,直至所有的正则表达式都被加入相应的分组中,这种算法的优点是减少了正则表达式之间的相互影响,存储空间使用较小,并且状态爆炸问题可以得到抑制[6,8-9]. 为了抑制状态爆炸问题出现,分组是一个非常有效的办法,但是消除状态爆炸,就需要进行大量分组,这样会增加分组数量,需要很多DFA 才能覆盖所有规则,这样会降低匹配引擎的效率. 判断正则表达式集合分组是否有效,既要考虑时间复杂度,又要考虑空间复杂度.本文通过自动学习的方式对规则分组进行优化,根据历史记录将正则表达式进行分组,然后将这个历史记录分组缓存到一个存储空间中,所以当进行匹配时,如果在该缓存中已经有了相应的记录,就不需要重新构建DFA,就可以根据历史记录来决定相应操作,从而避免重复增加状态来模拟排列组合现象,减少开销,在实际应用中,如果规则集已知的情况下,根据历史记录进行规则分组具有一定的意义. 为验证算法的有效性,本实验从开源的入侵检测系统Snort 中抽取若干条正则表达式作为测试对象,实验环境是在虚拟机中实现,操作系统为Intel i7处理器,内存4 GB,操作系统为ubuntu 18.04LTS,表1 为算法的性能数据,图3 是采用Snort 测试规则集的DFA 状态总数的变化图,由该图可知,随着迭代次数的变化,DFA 状态的总数量的变化会降低,当迭代约三次以后,DFA 状态的总数量基本上不再有明显变化,从而可以得出,该算法能较快得到最优情形. 表1 根据历史记录进行分组的算法性能指标 图3 DFA规则分组数与状态总数对应显示图 模式匹配作为IDS 的一种主要应用,其效率高低直接影响IDS 的性能优劣.在由正则表达式构造DFA 时,因为会产生状态爆炸情况,导致在存储空间和匹配速度上性能不佳.采用分组算法可以在一定程度上抑制状态爆炸问题,通过自动学习的方式,根据历史记录将正则表达式进行分组,当缓存中存在相应记录时,不需要重复构建DFA,从而提高性能.实验证明,该算法在规则集一定的情况下,能够减少状态总数,在空间复杂度上有一定的优化,能够在一定程度上抑制状态爆炸的发生.

1.3 评价依据
2 有限自动机


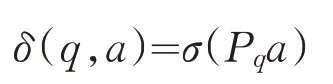
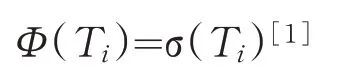

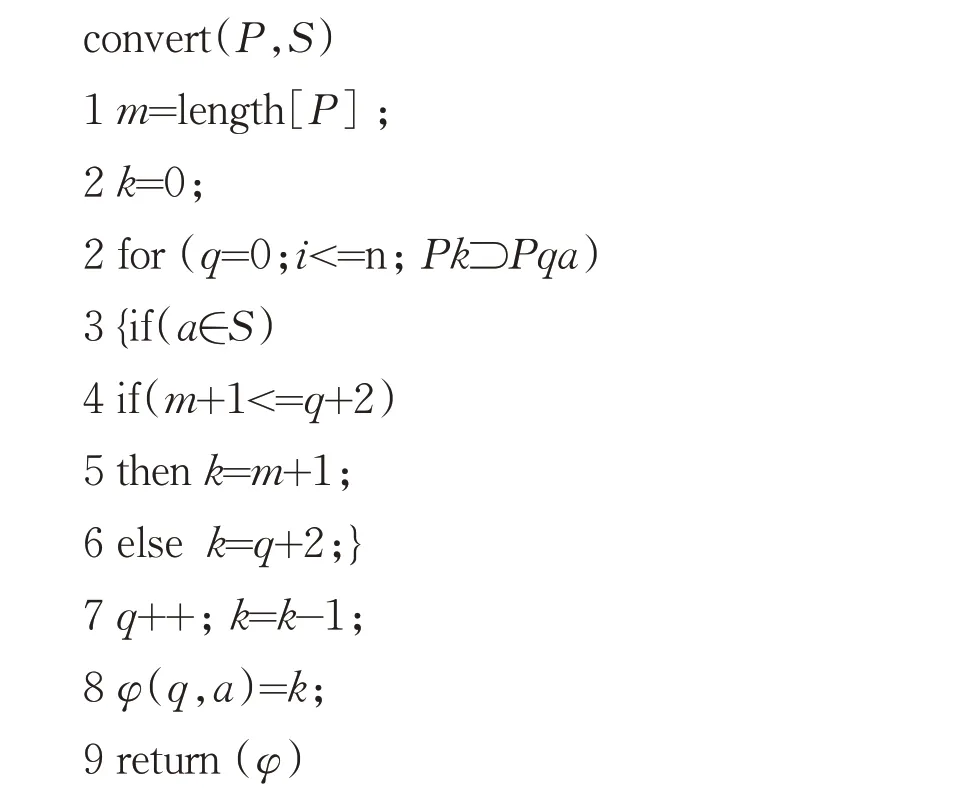
3 基于规则分组的匹配算法
4 仿真实验


5 小结

