数字滤波初始化方案在高分辨率GRAPES 区域模式中的应用研究*
庄照荣 李兴良 刘 艳 陈春刚
1.国家气象中心,北京,100081
2.中国气象局数值预报中心,北京,100081
3.西安交通大学,西安,710049
1 引言
高分辨率同化系统不仅同化常规观测资料,还同化高频率高密度雷达和卫星等非常规观测资料。高分辨率分析场作为数值模式的初值对千米尺度的模式预报质量非常重要。分析场中引入非规则分布的观测信息后,分析要素之间不满足准平衡关系,而分析变量之间的不平衡噪音在模式积分过程中会激发出没有气象意义的高频振荡重力波,严重时会影响模式预报质量和稳定性。为了抑制虚假重力波在模式中快速增长,在分析要素进入模式预报系统之前需要进行初始化过程。
重力波的控制可以通过调整初值中的重力波分量来实现,方法主要有牛顿松弛(Bao,et al,1997)、非线性正规模(Daley,1979;Williamson,et al,1981)、数字滤波和增量分析更新初始化等。目前牛顿松弛和非线性正规模初始化方案在数值预报模式中很少应用,而数字滤波和增量分析更新方案因有很好的初始化效果,在许多数值预报模式中被广泛使用。最初的数字滤波为绝热数字滤波(ADFI:Adiabatic Digital Filter Initialization)初始化方案,该方案分别向前和向后模式积分,而且都关闭物理过程(Lynch,et al,1992),对于当时6 min 时间步长的模式,采用3 和6 h 的截断周期都可以滤除高频噪音,并获得相似的结果,但12 h 的截断周期会阻尼气象模态的发展。虽然绝热数字滤波初始化增量改动较小,但是由于采用的绝热模式和后来模式预报使用的非绝热模式不一致,造成该初始化方案不能控制非绝热模式产生的噪音,因而又提出了非绝热数字滤波方案(DDFI:Diabatic Digital Filter Initialization)(Huang,et al,1993,1994;Lynch,et al,1997)。Huang 等(1993)研究指出,非绝热滤波方案采用向前非绝热积分的时间序列场进行滤波,其预报产生的噪音程度比绝热数字滤波方案低,同时考虑到较长的截断周期影响计算时效,通过最优滤波设计对于6 min 时间步长可采用最小滤波周期如2—3 h 的截断周期就可以达到可接受的初始化结果。由于数字滤波方案简单有效,在许多数值预报中心的四维变分同化系统中也将数字滤波作为目标函数的约束项进行初始化过程(Polavarapu,et al,2000;Gauthier,et al,2001;Wee,et al,2004;王舒畅等,2011;刘艳等,2019)。由于非绝热数字滤波初始化增量比较大,并且模式绝热向后积分过程中地面变量是保持不变的,但在非绝热模式向前积分时,随着积分步长变化的高空变量和保持不变的地面变量并不匹配。进而又提出了增量数字滤波方案(IDFI:Incremental Digital Filter Initialization)。该方案只有很小的初始化增量,不仅能减少动力热力调整时间,还能保持背景场快速增长的模态(Lynch,et al,1994)。但是增量数字滤波的计算量比非绝热数字滤波翻倍,而且若背景场有噪音,对模式预报也有隐患。增量分析更新初始化方案(IAU:Incremental Analysis Updating)通过在一段时间里把瞬时分析增量平滑地插值到预报模式系统来缓解分析场引入模式产生的噪音(Bloom,et al,1996;Polavarapu,et al,2004)。在快速更新分析预报循环系统中增量分析更新初始化方案提高了湿度场和动力场的平衡,因而能加快极小化过程和减少模式预报的动力、热力调整时间(Lee,et al,2006)。由于数字滤波的初始化效果较好并容易实施,因此,全球/区域分析和模式预报系统(GRAPES:Global/Regional Assimilation and Prediction System)中都采用非绝热数字滤波方案(薛纪善等,2008,2012)。在GRAPES-3DVar 分析与预报系统中,资料同化和初始化是两个独立实施的过程,会增加计算量。当同化系统升级到全球四维变分同化时进一步发展为弱约束的数字滤波初始化方法,约束强加在分析增量上与极小化迭代过程同步进行,数字滤波初始化方案是变分同化系统的一部分,不会对四维变分产生额外的计算资源消耗(刘艳等,2019)。
目前GRAPES-RAFS(RAFS:Rapid Analysis and Forecast System)分析预报循环系统分辨率从10 km 升级为3 km,原数字滤波方案是否适用?非绝热数字滤波方案是否能滤除高频噪音而又不影响预报质量等问题都有待解决。有研究表明,在高水平分辨率模式系统中有天气意义的波动与高频噪音的界限更加模糊,数字滤波初始化能对特定切断频率的高频振荡进行滤波,但无法区分滤除的信号是具有天气意义的高频信号还是虚假的高频噪音。而要消除积分过程中的高频振荡,必须延长滤波时间窗,但这是以增加额外积分时间以及有可能损害气象上有意义的波动为代价的(陈敏等,
2012)。
文中研究不同截断频率的非绝热数字滤波和增量数字滤波初始化方案在3 km 分辨率GRAPES区域模式中的应用情况,分析不同数字滤波方案对初始场和预报场的滤波效果,以及通过批量GRAPESMESO 和GRAPES-RAFS 试验考察不同初始化方案对气象要素预报质量的影响。
2 数字滤波方案
2.1 非绝热数字滤波
按照数字滤波的理论(Lynch,et al,1992;Huang,et al,1993),通过对短时间内的模式预报场进行时间滤波可以滤除高频部分噪音,在GRAPES区域模式系统中的数字滤波方案采用非绝热数字滤波(薛纪善等,2008,2012),即

若非绝热数字滤波的截断周期为T,Δt为时间步长,则在周期内时刻序列 k取值为-N 到 N,N=T/(2Δt),fk为截断周期-T/2到T/2时段,离散时刻 k 的计算值,f0*为滤波后的初始场。非绝热数字滤波方案先把分析场通过模式绝热向后积分到-T/2处,然后在-T/2处模式非绝热向前积分到T/2处,此时 fk为从-T/2到T/2时段内模式非绝热向前积分的预报场,如图1 所示。Hk为数字滤波系数,即


图1 非绝热数字滤波初始化方案示意Fig.1 Schematic diagram of diabatic digital filtering initialization scheme

式中,Tc为截断周期。从式(3)可以看出,当模式的时间步长确定,截断频率随着截断周期而变化,

从以上公式可知,非绝热数字滤波方案为通过对一段时间的模式积分预报场进行时间滤波,滤波效果与截断周期有关。定义转换函数T(θ)为一次滤波过程,若fk=eikθ,f0*=T(θ)·f0,其中i 为虚数单位,θ 为频率,f0为k=0 时的气象场,由于对称系数Hk=H-k,代入式(1)可得(Lynch,et al,1992),

从T(θ)函数可以看出滤波过程中不同截断频率下高频信息滤除的程度。图2 为模式时间步长30 s情况下不同截断周期下的转换函数变化情况,可以看出理想截断频率为0.1。当选用不同的截断周期,转换函数分布大不相同。截断周期为2 h 时,0.05 以上频率的信息滤除过多;截断周期为30 min时,频率0.25 以上的波动都被滤除,截断周期为15 min,频率0.45 以上的信息大部分被滤除。也就是说截断周期越短,保留的高频信息越多。从图2中也可以看出,当不使用窗函数时,同样截断周期的转换函数在高频部分会有不稳定波动,采用窗函数后,不稳定波动噪音也被滤除。

图2 不同截断周期下的转换函数Fig.2 Transfer functions for the filter with different cutoff periods Tc
数字滤波为时间滤波,滤波系数 Hk相当于在滤波区间内对各预报场所取的权重,即滤波区间内各预报场对初始场的影响程度。时间步长为30 s 的水平分辨率3 km 模式中,滤波系数与截断周期的关系如图3 所示。可以看出,当截断周期越长,滤波系数在初始时刻的权重越小;截断周期越短,滤波权重在初始时刻越大。意味着截断周期越长,分析时刻模式预报场占的比重越小,通过滤波区间内所有模式场的影响,滤除了分析场中可能引起虚假重力波的噪音。
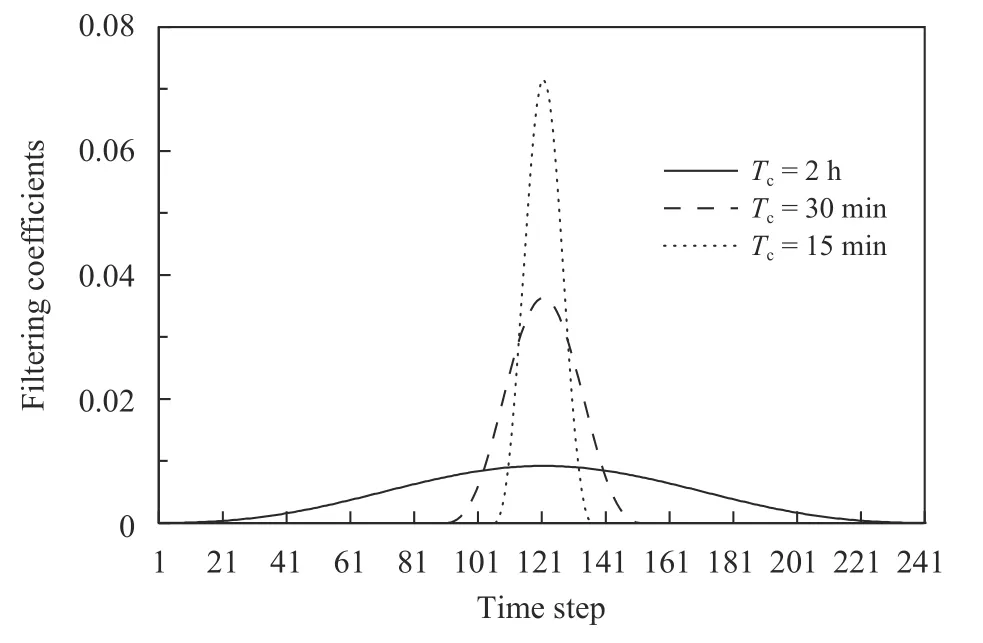
图3 不同截断周期下的滤波系数Fig.3 Filtering coefficients with different cutoff periods Tc
2.2 增量数字滤波
在非绝热数字滤波方案中,对分析全量滤除了噪音,但实际上背景场是模式预报场,变量之间通常是协调的,一般假定背景场没有噪音,因而只对加入不规则观测资料信息后的分析增量进行滤波。文中采用增量数字滤波方案,即

式中,xb为背景场,为对背景场进行非绝热数字滤波,为对分析场进行非绝热数字滤波,增量数字滤波的初始场 xini是在原背景场上叠加滤波后的分析增量。增量数字滤波的优点为可以保留背景场中快速增长的模态,也可以加速动力、热力调整过程,获得更小的初始化增量。但由式(6)可见,增量数字滤波需要分别对背景场和分析场进行非绝热数字滤波,因而滤波过程比非绝热数字滤波初始化方案增加了1 倍计算量。
3 GRAPES-MESO 数值预报试验
3.1 试验设置
为了测试数字滤波方案的影响,文中对GRAPES区域模式系统进行5 组数字滤波试验,试验时段为2018年6月12日00 时—28日12 时(世界时,下同),试验范围为中国东部(17°—50°N,102°—135°E),模式分辨率为3 km,垂直为51 层,模式层顶高33 km。试验在GRAPES-3DVar 分析和云分析的基础上进行不同数字滤波初始化方案,预报时效为24 h,GRAPES 区域模式时间步长30 s,各组试验采用相同的GRAPES 区域模式物理过程参数设置。不同数字滤波初始化方案的试验设置见表1。

表1 试验设置Table 1 Experiments design
Ana 为对照试验,直接采用分析结果进行预报,不做数字滤波初始化处理。T2h 试验按照业务水平10 km 分辨率 GRAPES-RAFS 的数字滤波设置,滤波截断周期为2 h。T30/T15 试验的数字滤波截断周期分别为30 min 和15 min,T30inct/T15inct试验为在T30/T15 试验基础上进行的增量数字滤波,保留了背景场中所有高频信息。
数字滤波初始化方案主要用来抑制初始时刻动力场和质量场不协调激发出来的高频振荡噪音(Lynch,et al,1992;薛纪善等,2008),因此文中仅对模式层上的无量纲气压、位温、U、V 和W 风场进行数字滤波初始化过程,未调整湿度场,与区域GRAPES-3DVar 和全球GRAPES-4DVar 业务中设置相同(刘艳等,2019)。
3.2 滤波效果分析
文中在批量试验中选取2018年6月15日00 时的初始场和预报场进行分析,研究采用数字滤波初始化方案后对初始场和预报场的滤波效果。
3.2.1 初始场影响
从2018年6月15日00 时模式面第24 层的初始场U 风场(图4)可以看出,经过三维变分分析后,U 分析风场有更多细微信息(图4a),当滤波截断周期从15 min(图4d)、30 min(图4c)到2 h(图4b),U 风场逐渐滤除较多的中小尺度信息,T2h 试验的初始U 风场已经非常平滑。如果采用增量数字滤波,T30inct 与T15inct 的初始U 风场都非常接近Ana 试验,T15inct 与Ana 的初始风场差别最小。
初始化方案目的是在尽可能小的改动分析场基础上,使初始场更协调,减小分析噪音。因而初始化方案的改动要相对小于分析增量场,不影响分析质量。表2 统计2018年6月15日00 时不同数字滤波方案的初始化增量(初始场减去分析场),以及Ana 试验的分析增量(分析场减去背景场)全场平均的均方根误差(RMSE)以及绝对最大值(MAX)情况。
从表2 可以看出,数字滤波方案各个变量的初始化增量的均方根误差都比分析增量的均方根误差小,而且滤波周期越短,对分析场的改动越小,初始化增量的均方根误差越小。对于同样的滤波周期,增量非绝热数字滤波方案明显比全量非绝热数字滤波方案对分析场改动的少。5 组数字滤波试验中的T15inct 初始化增量的均方根误差最小,初始场最接近Ana 试验,与图4 的结论一致。由于没有对湿度变量进行数字滤波初始化,湿度初始场即为分析场。T2h 方案采用的滤波周期太长,最大初始化增量比分析增量大得多,从图4 也可以看出T2h 方案对分析场改动过大,初始场太平滑;T30与T15 数字滤波方案的最大初始化增量与最大分析增量基本相当;T30inct 与T5inct 方案的最大初始化增量明显小于最大分析增量。

表2 2018年6月15日00 时不同试验的分析增量与初始化增量Table 2 Analysis increments and initialization increments at 00:00 UTC 15 June 2018
3.2.2 功能谱分析
上一节主要从时空域分析不同初始化方案中初始场的差别,本节从频谱空间研究不同数字滤波初始化方案对初始场的影响。文中采用二维离散余弦转换(2D-DCT:Discrete Cosine Transform)方法对有限区域二维气象场进行谱分解(郑永骏等,2008;庄照荣等,2018,2020),比较不同数字滤波方案的初始场(xinit)与分析场(xa)的功率谱差别(即初始化增量功率谱)。为了便于比较,文中对初始化增量功率谱的绝对值取对数(即:lg|xinit-xa|)。从2018年6月15日00 时模式面第24 层不同初始化方案的初始化增量功率谱(图5)可以看出,对于无量纲气压变量,由于其本身随时间的变率很小,不同初始化方案的初始化增量功率谱差别很小。对于位温变量,不同初始化方案的初始化增量功率谱在339 km 以下部分差别比较明显,其中T2h 试验的初始化增量功率谱最大,其次是T30 试验,T15试验和两组增量数字滤波方案的初始化增量功率谱差别不大。对于风场变量,不同初始化方案的初始化增量功率谱差别很大。T2h 试验的初始场和分析场的功率谱相差最大,并且不仅在中小尺度部分有较大差别,在大尺度部分差别也非常明显。说明T2h 试验的初始化方案滤除了有气象意义的波动信息。T30 试验的初始化增量功率谱进一步缩小,T15 试验的初始化增量功率谱又进一步下降。同样,两组增量数字滤波方案的风场初始化增量功率谱相当,并且在几组试验中最小,说明增量数字滤波方案能保留更多的中小尺度信息。从图5 还可以看出,在不同波段上,不同初始化方案的初始化增量功率谱差别也有所不同,例如T2h 试验在所有波段上的风场增量功率谱和其他初始化方案的差别都很大,T30、T15 试验及同一截断周期的增量数字滤波试验的风场初始化增量功率谱的差别主要在641 km 以下尺度范围内。这也说明T2h 试验的初始风场与分析场差别在大尺度上都比较明显,T30、T15 试验的初始风场与分析场的差别主要在中小尺度信息上,与图4 结果一致。

图4 2018年6月15日00 时第24 层初始U 风场(a.无数字滤波,b.2 h 数字滤波,c.30 min 数字滤波,d.15 min 数字滤波,e.30 min 增量数字滤波,f.15 min 增量数字滤波;单位:m/s)Fig.4 Initial fields of U-component at the 24th model level at 00:00 UTC 15 June 2018 for different experiments(a.No DFI,b.DDFI with Tc=2 h,c.DDFI with Tc=30 min,d.DDFI with Tc=15 min,e.IDFI with Tc=30 min,f.IDFI with Tc=15 min;unit:m/s)

图5 2018年6月15日00 时第24 层分析场与数字滤波后的初始场功率谱差别(a.无量纲气压,b.位温,c.U 风场,d.V 风场;单位:m3/s2)Fig.5 Power spectra of analysis minus initial field at the 24th model level at 00:00 UTC 15 June 2018(a.non-dimensional pressure,b.potential temperature,c.U-component,d.V-component;unit:m3/s2)
3.2.3 预报场影响
分别选取海上和平原两点来考察采用不同数字滤波方案后预报的地面气压变化情况。从3 h 地面气压预报(图6)可以看出,数字滤波周期越长,信息滤除越多,地面气压随时间演变越平滑。而增量数字滤波保留了背景场中所有信息,因而地面气压变化略比同样滤波周期的非绝热数字滤波波动大,其中周期为2 h 的数字滤波方案使地面气压变化过于平滑。比较海上和平原两点的地面气压变化也可以看出,在预报前1 h 内平原上地面气压变化幅度明显大于海上,随后平原上地面气压随时间积分增加,其变化幅度有所减缓。
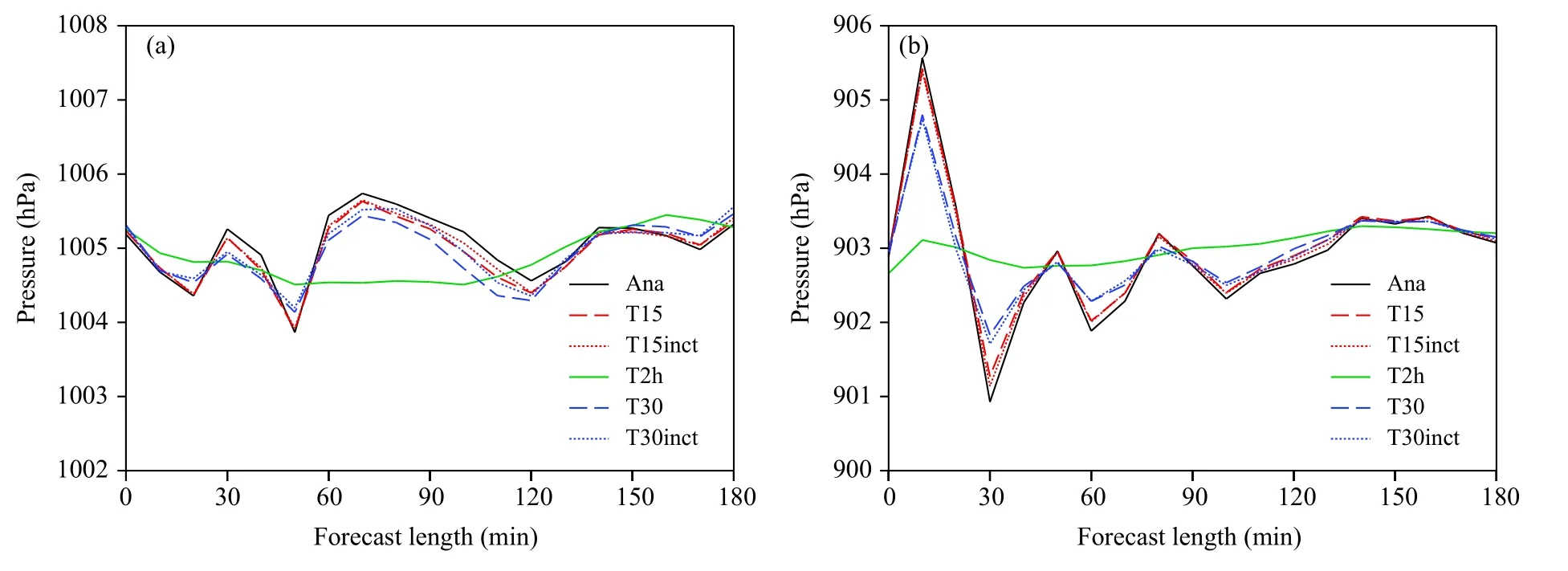
图6 前3 h 预报的地面气压变化(单位:hPa;a.海上(30°N,128°E),b.平原(30°N,108°E))Fig.6 Surface pressure variations(unit:hPa)in the first 3 h at two model grids(a.ocean point(30°N,128°E),b.land point(30°N,108°E))
从全场平均的地面气压倾向(图7)可以看出,初始时刻的地面气压倾向最大,随着预报步数的增加,变量间进行调整,气压倾向逐渐减小。在前3 h 预报中,滤波周期为15 min(T15 试验)的地面气压倾向略低于对照试验,滤波周期30 min 的地面气压倾向比T15 试验进一步减小,但预报3 h 后,Ana、T15、T30 的地面气压倾向的差别越来越小。当滤波周期为2 h时,初始地面气压倾向就很小,约0.14 hPa/(10 min),随着模式积分,前3 h 的地面气压倾向略微减小且趋于稳定,说明T2h 试验虽然消除了分析噪音,但只保留了大尺度部分信息,因而变量之间很协调,气压倾向非常小。T15inct,T30inct 的增量数字滤波方案的地面气压倾向几乎与同样滤波周期的非绝热数字滤波方案重合,可以达到非绝热数字滤波滤除噪音的效果,同时也保留背景场中协调的气象场信息。

图7 2018年6月15日00 时起报的地面气压倾向(单位:hPa/(10 min))Fig.7 Surface pressure tendency starting from 00:00 UTC 15 June 2018(unit:hPa/(10 min))
3.3 批量试验结果
为了研究不同数字滤波初始化方案对预报质量的影响,本节将不同初始化方案的数值预报试验结果与观测要素进行比较,考察初始化方案对高分辨率天气预报的影响。
3.3.1 气温及风预报场
比较17 d 地面气象要素24 h 预报与观测的平均偏差(图8),对于前12 h 预报,不同初始化方案的2 m 气温预报略有不同,T2h 试验与Ana 试验无初始化方案的预报偏差差别最大,达0.1 K;T30 和T15 试验与Ana 试验预报偏差差别小于0.05 K;两个增量数字滤波方案的2 m 气温偏差与Ana 试验几乎相同,意味着增量数字滤波方案相对于同样滤波周期的全量数字滤波方案对预报场影响更小;对于10 m 风场,不同初始化方案与Ana 试验的预报偏差几乎没有区别。对于12 h 后的预报,不同初始化方案对地面气象要素预报几乎没有影响。

图8 地面气象要素预报的平均偏差(a.2 m 气温,单位:K;b.10 m U 风场,单位:m/s;c.10 m V 风场,单位:m/s)Fig.8 Biases of average forecast fields(a.2 m temperature,unit:K;b.10 m U-component,unit:m/s;c.10 m V-component,unit:m/s)
无论对2 m 气温还是10 m 风场,不同初始化方案的预报均方根误差也几乎一样。对于高空气象要素场12 h 预报(图略),几组初始化方案对要素预报的全场平均预报偏差和均方根误差也几乎一样,表明初始化方案对12 h 高空气温和风预报场的影响可以忽略。
好的数字滤波方案的应用应使分析场改变很小且在可接受范围内,并能使预报质量不下降(Lynch,et al,1992)。由上述分析可知,文中不同数字滤波初始化方案对气温和风预报的影响很小,只有T2h试验的2 m 气温3 h 预报偏差与Ana 试验差别略大。
3.3.2 降水预报
这里采用常用的公平风险评分(ETS,Equitable Threat Score)来客观评估降水预报准确度。比较6 组试验各时段平均累计降水预报ETS 评分(图9)可以看出,不同初始化方案的降水预报质量略有不同,但差别并不显著。相对于Ana 试验,T2h 试验0—6 h 除暴雨量级外ETS 评分都略低于Ana 试验;6—12 h 不同量级降水的ETS 评分都明显低于Ana 试验;12—18 h 大雨ETS 评分显著低于Ana 试验,中雨和暴雨量级降水预报优于Ana 试验;18—24 h 从小雨到大雨ETS 评分都低于Ana 试验。总之,T2h 试验滤波截断周期过长,滤除了一些有气象意义的信息造成24 h 内整体降水预报质量有所下降。

图9 不同时段降水预报ETS(a.0—6 h,b.6—12 h,c.12—18 h,d.18—24 h)Fig.9 ETS of accumulated precipitation forecast at various forecast lead times(a.0—6 h,b.6—12 h,c.12—18 h,d.18—24 h)
T30 试验的降水ETS 评分0—6 h 大雨和暴雨时明显高于Ana 试验,12—18 h 除去大雨的其他量级降水都略高于Ana 试验;其他时段和量级降水都与Ana 试验评分相当或略低。当在滤波周期30 min基础上采用增量滤波时,相对于T30 试验,6—24 h中雨降水ETS 评分有所提高,6—18 h 大雨降水ETS 评分也有所提高。
T15 试验的降水ETS 评分0—6 h、12—18 h 大雨以上量级和Ana 试验的差别略大,其他时段和量级降水ETS 评分接近Ana 试验结果。T15inct 试验在各个时段和各量级的降水ETS 评分与T30inct 基本相当,二者的降水预报ETS 评分相对最接近Ana 试验。
4 GRAPES-RAFS 数值预报试验
在快速分析预报循环系统中,多次分析会造成初始场变量之间更加不协调,严重影响模式的稳定性,而初始化方案在循环中多次应用在降低分析噪音的同时,对模式预报质量也会有影响。本节在GRAPES-RAFS 分析预报循环中应用不同的数字滤波方案检验初始化方案对预报质量的影响。
4.1 试验设置
采用GRAPES-RAFS 进行一天两次(00/12 时起始)每3 h 循环的12 h 间歇分析预报试验,试验时段为2018年6月11—29日。每个循环过程开始时采用全球模式降尺度的预报作为背景场,循环过程中采用区域模式自身预报作为背景场,文中每次三维变分分析后都采用云分析,在分析场进入模式预报系统前进行数字滤波初始化,模式预报24 h。试验范围为中国东部(17°—50°N,102°—135°E),模式分辨率为3 km,垂直为51 层,模式层顶33 km。进行了两组数字滤波初始化试验,第一组采用2 h截断周期(即T2h),第二组采用15 min 截断周期(即T15),进行分析预报循环试验。为了测试不同初始化方案对快速分析预报循环试验的影响,本节主要比较分析预报循环12 h 后,分析00 时两组数字滤波初始化方案对分析场和预报场的影响。
4.2 气温、风及相对湿度检验
文中比较经过快速分析预报循环12 h 后,试验时段00 时的背景场、分析场与探空观测的17 d 全场平均偏差与标准差(图10),可以看出,采用不同数字滤波方案,在经过多次分析和模式预报后,T15 试验的背景风场偏差比T2h 试验更接近0 线,同时T15 试验的背景风场标准差从低层到高层也明显小于T2h 试验,分析风场结果类似(图10a、b)。不同数字滤波方案温度场(图10c)的背景场和分析场偏差相差均不大。T15 试验的背景场温度标准差略小于T2h 试验。不同数字滤波方案湿度场(图10d)的背景场和分析场偏差基本没有区别,标准差也相差不大。

图10 00 时分析场/背景场与探空观测的偏差(a1—d1)和标准差(a2—d2)(a.U 风场,单位:m/s;b.V 风场,单位:m/s;c.温度,单位:K;d.相对湿度,单位:%)Fig.10 Biases(a1—d1)and standard deviations(a2—d2)of analyses/background fields with radiosonde observations at 00:00 UTC(a.U-component,unit:m/s;b.V-component,unit:m/s;c.temperature,unit:K;d.relative humidity,unit:%)

续图 10Fig.10 Continued
综上可知,在快速分析预报循环中,经过多次数字滤波初始化,采用15 min 截断周期的数字滤波方案比2 h 截断周期方案对风场分析场和风场的3 h 预报场(背景场)有明显正贡献。
经过12 h 预报后,与T2h 试验相比,T15 试验的初始化方案对预报风场还有明显正贡献(图11),预报风场与探空观测的偏差从低层到高层比T2h试验更接近0 线,风场标准差也略小于T2h 试验。但12 h 预报的温度场、湿度场的偏差与标准差在两组试验中差别并不明显。
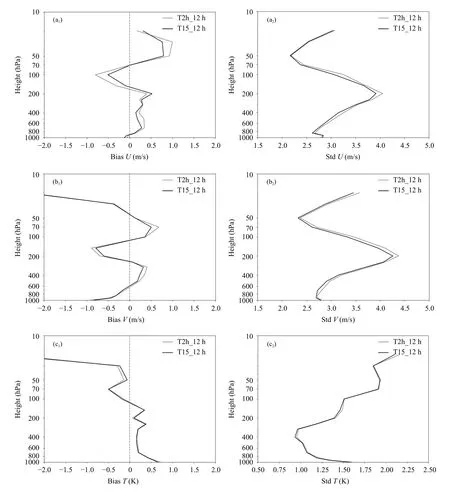
图11 12 h 预报场与探空观测的偏差(a1—d1)和标准差(a2—d2)(a.U 风场,单位:m/s;b.V 风场,单位:m/s;c.温度,单位:K;d.相对湿度,单位:%)Fig.11 Biases(a1—d1)and standard deviations(a2—d2)of 12 h forecasts with radiosonde observations(a.U-component,unit:m/s;b.V-component,unit:m/s;c.temperature,unit:K;d.relative humidity,unit:%)
4.3 降水预报
2018年6月12—28日12 h 循环后00 时起报的T15 和T2h 试验的平均每6 h 预报降水ETS 如图12 所示。可以看出,T15 试验的0—6 h 降水预报ETS 除中雨量级外其他各个降水量级都比T2h 试验显著提高,但T15 试验的6—12 h 降水预报ETS 在中雨和暴雨之间低于T2h 试验。12—18 h,T15 试验在小雨、中雨和大雨量级的ETS 显著高于T2h 试验;18—24 h,T15 试验的降水预报ETS在小雨和暴雨量级高于T2h 试验。整体来看,T15试验比T2h 试验对24 h 内降水预报有优势。
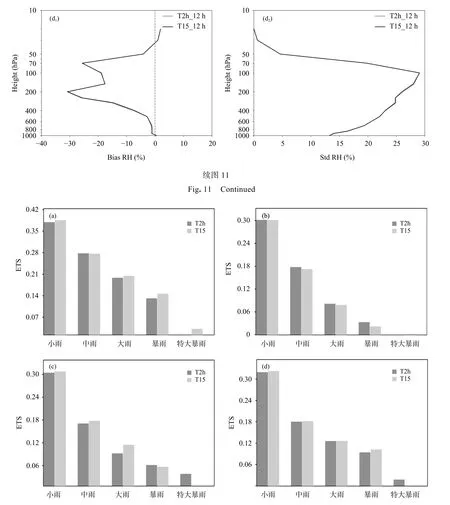
图12 不同预报时段降水ETS(a.0—6 h,b.6—12 h,c.12—18 h,d.18—24 h)Fig.12 ETS of accumulated precipitation forecast at various forecast lead times(a.0—6 h,b.6—12 h,c.12—18 h,d.18—24 h)
5 结论和讨论
对3 km 分辨率的GRAPES 区域模式采用非绝热数字滤波和增量数字滤波初始化方案抑制虚假重力波在模式中的增长,研究不同截断周期的数字滤波方案对分析和预报的影响。通过滤波效果分析及数值预报批量试验,得到以下结论:
(1)对水平3 km 分辨率,模式时间步长30 s 的GRAPES 区域模式,2 h 截断周期的初始场过于平滑,滤除了有气象意义的信息。30 min 与15 min 截断周期的初始场既滤除了高频噪音,也基本保留了有用的分析信息。而增量数字滤波方案可以保留背景场中快速增长的模态,只滤除分析增量不协调的噪音。几组方案中T15inct 试验的初始化增量最小,初始场最接近分析场。从功率谱分析也可以看出不同数字滤波方案对初始动力场影响最大,两组增量数字滤波方案保留了更多的动力中小尺度信息,与分析场的功率谱差别最小。
(2)GRAPES-MESO 的批量数值预报试验表明,不同数字滤波方案对12 h 内预报的地面2 m 温度场影响略有不同,几组初始化方案中初始场与分析场的平均偏差最大可达0.1 K,而对地面10 m 风场预报影响不大。不同数字滤波方案对高空气象要素12 h 预报场的影响也不大。不同数字滤波方案对降水预报的影响略有不同,T2h 试验整体降低24 h 内降水预报的ETS,T30inct 与T15inct 试验的降水预报ETS 相对更接近Ana 试验。
(3)GRAPES-RAFS 的批量数值预报试验表明,经过多次分析预报循环后,初始化方案对分析和预报的影响会逐渐累积,因而不同初始化方案的分析预报质量有明显的区别。T15 试验对风场分析和12 h 预报比T2h 试验有明显正贡献,同时T15 试验24 h 内各时段的降水预报质量也整体优于T2h试验。
对于高分辨率模式,由于高频噪音与具有天气意义的高频信号很难区分,增量数字滤波能避免破坏初猜场的气象信息,因而在计算效率和资源有保障的情况下,增量数字滤波初始化方案是更优选择。另外,在能消除积分过程中的高频振荡基础上,较小滤波截断周期可以节约一定的计算时间,也能最大限度地保留有气象意义的高频信息。因而需要在高分辨率模式中选择合适的数字滤波参数来保证中小尺度的预报质量。
文中只对动力场和质量场进行数字滤波,而对于湿度变量以及相关的水成物变量的噪音没有进行处理,云分析后水成物变量是通过松弛逼近(nudging)方式吸收到模式中(朱立娟等,2017)。虽然初始化方案主要用来抑制初始动力场和质量场不平衡而激发的虚假重力波,但一般在数字滤波方案中湿度变量也进行了初始化过程(Lynch,et al,1992),而且在间歇循环中对云水的初始化过程能缓解云水和其他变量的不平衡,同时缩短云和降水产生的调整适应时间(Huang,1996)。因而下一步工作将对GRAPES-RAFS 中的水成物变量和其他变量的协调性进行研究。由于非绝热数字滤波需要绝热向后积分,然后再向前积分,在高频同化及高分辨率系统中会占用计算时间,而增量数字滤波方案不仅对分析场还需要对背景场进行非绝热数字滤波,因而在实施过程中又增加了计算时间。此外,在快速分析预报循环中,若背景场的预报时效不长,变量之间难以达到平衡,背景场也可能存在一些噪音,因而增量数字滤波初始化方案是否能有效滤除噪音而保持模式稳定运行还需要进一步研究。同时,在高分辨率模式下,很难区分高频噪音和有气象意义的小尺度波动,因而采用的数字滤波方案也有可能影响中小尺度系统的预报质量。今后针对千米尺度的高频快速分析预报循环系统,也需要寻求其他能满足业务运行时效要求的初始化方案,例如增量分析更新初始化方案。

