基于自营式外卖的配送路径优化问题
◇南京农业大学信息管理学院 王淑雅
近年来外卖行业迅速发展,在快消费时代引起了一股浪潮,然而随着外卖业的发展,如何提升外卖服务业的水平也成了热门话题,其中外卖配送路径的优化问题有为重要,其直接影响到了顾客体验以及配送成本。本文主要针对商家自营式外卖配送形式,立足于实际案例,通过TSP规划求解以及节约算法解决单配送车辆不考虑载重、多配送车辆考虑载重、多配送车辆考虑载重与时间窗的外卖配送路径优化问题,并对三种方案进行对比,分析其可行性进而实际解决某餐厅的外卖配送路径设计问题。
配送问题一直都是各生产企业、物流企业所关心的问题,商品的运输与配送是从连接市场与消费者,实现商品价值的重要步骤。随着经济形式的多样化,末端配送已经随处可见,在当下热门的外卖行业中,配送直接影响着外卖行业的成本以及顾客的满意度,其中成本包括时间成本、油耗成本等,而顾客的满意度主要体现在外卖是否能够准时安全到达上,所以无论从商家角度还是顾客角度实现配送路径更加优化都是至关重要的。
1 背景介绍
1.1 我国外卖现状
随着“互联网+”商业模式的迅速发展,互联网餐饮行业也得到了快速的发展,其中外卖在全国餐饮消费总额的比重越来越大。据统计,2014年,全国餐饮消费总额数为4500亿元,按照16%的餐饮年增幅,2016年全国餐饮消费总额预计将达到7000亿元。其中,外卖占去拿过餐饮消费总额的10%,截止2016年,外卖市场规模预计将要达到700亿元[1]。近年来,众多的外卖APP也在抢占市场,其中最具有代表性的有“美团”、“饿了么”、“百度外卖”等外卖平台,这些平台的构建反过来也促进了外卖行业的发展,外卖行业不断壮大已经成为了必然趋势。具体情况如表1所示[1]。

表1 我国互联网外卖商家现状
随着外卖需求的不断增加,对外卖服务质量的要求也进一步提升,其中外卖配送作为外卖行业的重要环节受到了各大平台以及顾客的广泛关注。在配送过程中配送路径的选择决定了配送的时间,进而直接决定了外卖服务的质量。而在现实生活中配送员选择配送路径往往都是通过经验进行主观判断,这样不仅会导致配送效率低下,更有可能造成配送时间不在规定范围,产生等待成本或者惩罚成本,使顾客的满意度受到印象,进而影响提供商的品牌效应,因此对配送路径进行优化是非常重要的。
1.2 商家自营式外卖配送形式
目前主流的配送形式主要有:商家自营配送、雇佣配送员配送、外卖平台配送。本文的主要介绍自营式外卖配送形式。所谓商家自营配送就是点餐者从消费端下单后,经由外卖平台传达至商家,商家承担起了备餐、配送的任务,将包装好的食物送至点餐者手中。大多数商家位于配送需求点附近,配送者对配送路线十分了解,在配送过程中会选择最为“经济”的路线,用最短的时间配送最多的单数。这种配送方式带给消费者的体验因商家而异,配送效率越高的商家,消费者对于此次消费的体验相对更满意[2]。
这种配送形式的主要特点是由商家直接配送,即商家派出配送员进行若干配送点的配送,配送员完成配送任务后要返回商家,是一个闭环线路的配送问题。商家自营式外卖配送的优点在于配送员只需要在一个商家处取货,取货形式相对简单,出发点与终点固定。目前这样的配送方式主要应用于公司或者学校附近这样外卖需求较大的地段。
1.3 研究内容
本文基于外卖现状的大背景下,针对商家自营式外卖这一具体外卖配送形式进行研究,主要解决自营式外卖的外卖配送线路优化问题,帮助其摆脱“经验模式”,而可以通过实际的运算分析得到科学的配送路径,以高效率地服务顾客,满足顾客需求,同时尽可能地降低时间成本。
本文主要解决三大问题:
(1)通过TSP规划问题EXCEL求解法求解单车辆、无载重约束下的配送路径优化方案。
(2)通过节约算法通过EXCEL求解有载重约束条件的配送路径优化方案,并求解出所需要的配送车辆数。
(3)在(2)的基础上考虑时间窗约束,对节约算法进行深化求解时间窗与载重同时约束下的配送路径优化方案与所需配送车数量。
在求解三种情况下的配送路径优化方案后进行对比,总结各自的优缺点,进而说明优化方案的可行性。
2 案例分析
2.1 案例介绍
本文所研究的案例背景来源于翟劲松[3]论文中的实例,以下数据均来自该论文。以某餐厅(编号0)为背景,在某天11:30到12:30时间段内对其9个配送点(编号1到9)进行外卖配送服务,已知各配送点之间的配送时间和到商家之间的行驶时间如表2所示。
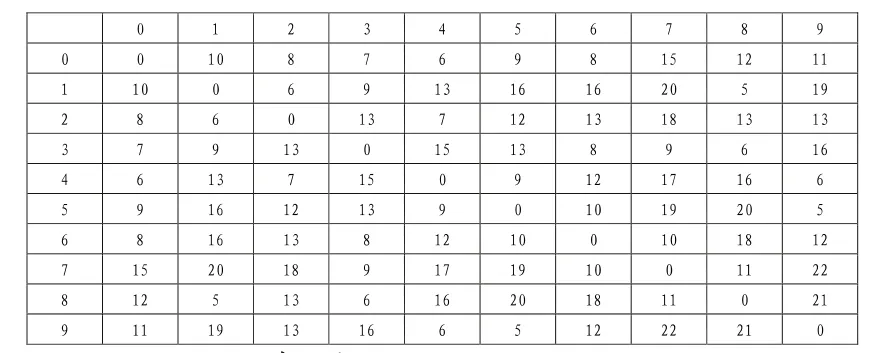
表2 各点之间的行驶时间
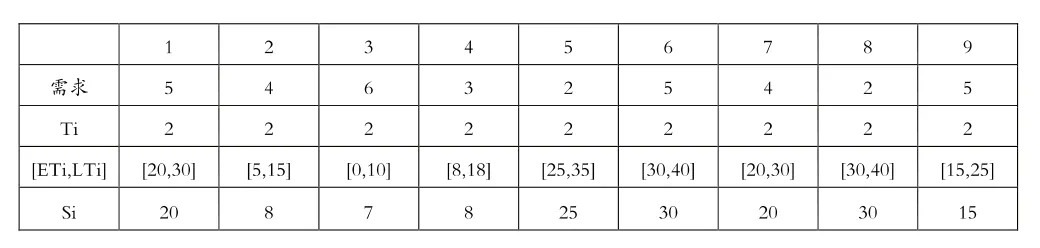
已知各顾客点的需求量以及顾客点需求的时间窗如表3所示,且商家所拥有的配送车辆最大载重量为15份。
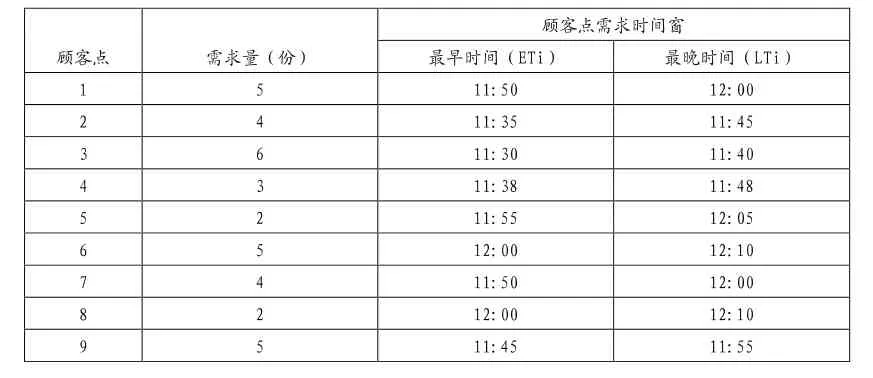
表3 各点的需求量和时间窗
2.2 问题解析
本文设定该餐厅为自营配送式餐厅,采用商家自行配送的方法,商家在接到订单后派出配送员对9个顾客需求点进行配送,配送完毕后回到商家处。本文所要解决的问题即如何科学合理的规划配送路径,使得商家可以以最低的成本获得最大的效益,同时顾客可以达到期望的满意度。
本文采取层层推进的逻辑方式,首先对于该问题进行最简单的巡回路径规划,即TSP问题规划,在一辆配送车辆无时间限制、装载限制的条件下进行不重复的路径配送,遵循单回路、单一性、遍历性的原则设计配送路线。其次,在配送车辆具有装载容量限制的情况下,规划多配送车辆多回路的配送辆路径,并可以求得适当的配送车辆数。最后在考虑时间窗于长在容量的情况下,即使得客户满意度最高的情况下进行配送路径规划,求得所需要的配送车辆以及各个点到达的具体时间,并对三种结果进行对比得出有关配送路径优化的最终结论。
3 优化方法
3.1 TSP问题路径优化法
TSP(TravelingSalesman Problem)自1959年提出已经过去了半个多世纪,TSP问题是一个NP难问题,目前为止都没有一种高效且精准地求解方法。高效精准地求解TSP问题在车辆路径规划、O20物流配送等很多领域都有着非常重要的意义。TSP问题的目标是在一系列点集中寻找一条最短回路,并要求每个点只访问一次,目前主要的求解方法为启发式智能算法,如遗传算法、蚁群算法和蝙蝠算法等[4]。
由于本文所解决的问题相对来说较为简单,所涉及到的顾客点较少,因此可以直接通过混合整数线性规划算法求解,用EXCEL构建规划求解模型配以适当的约束条件即可。
3.2 节约算法
节约算法又称为节约里程算法,是在满足某些约束条件下将两个以上的回路合并成一个回路后实现总的运输距离缩短的方法。这种方法可以解决在车辆数目不确定的配送路线的优化问题,可以解决共同配送给中路径、人员等问题[5],在路径优化问题中有着广泛的应用。
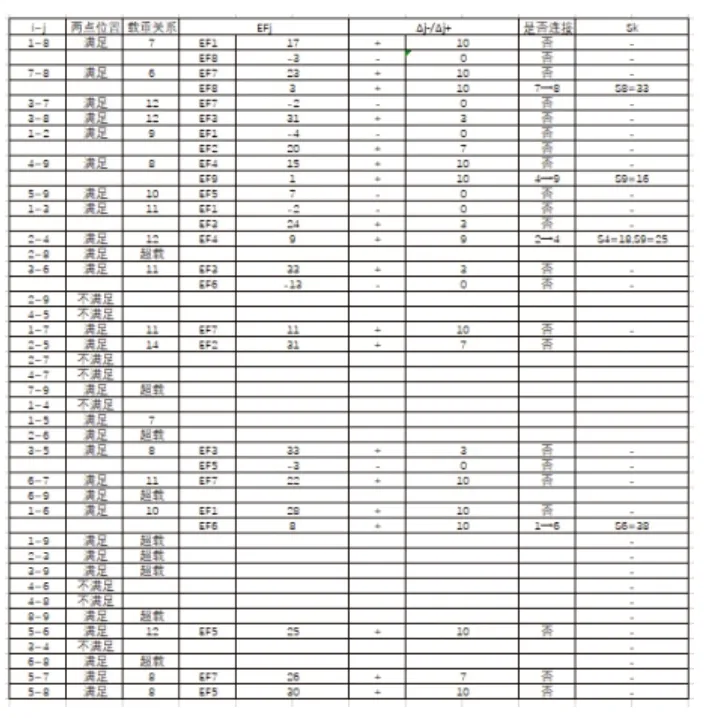
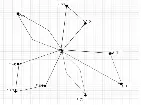
其思路为,假设P点为配送中心,A和B是两个需求点,PA的距离为a,P-B的距离为b,A-B的距离为c。在初始情况下P分别对A和B进行配送,即从P-A-P,所需要的距离为2a,从PB-P,所需要的距离为2b。而此时如果将A-B连接,即A和B不需要单独配送,而通过一次配送就满足,那么路径就改变为PA-B-P,所需要的距离为a+b+c。此时需要比较2a+2b与a+b+c之间的数量大小关系。假设不考虑载重量的问题,当2a+2b>a+b+c时则采用第二种配送路径,当2a+2b 图1 节约算法思路图 节约算法的主要步骤为:①计算各个需求点之间的最短距离;②使用节约里程法进行计算。两个需求点之间的节约里程为两个需求点与配送点之间的距离之和减去两个需求点之间的最短距离;③对节约里程数进行排序;④形成初始解。在满足车辆限载、客户需求量大小、时间限制等等所有条件的限制下,根据第一步的得到的最短路径,进行配送点与需求点之间一对一直达配送,计算得出总里程数;⑤对回路进行合并,得出路径优化方案。从节约里程排序中找出产生该节约里程的两个配送点i、j,再判断连接 i、j的回路是否存在合并的可能性。如果一个回路是以(p,i)开始,最后以(j,p)结束,同时满足车辆配载,时间因素等多种限制,那么这个回路可以进行合并。删除两个回路中的部分路径,然后引入新的连接(i,j),得到新的回路(p,...,i,j,...,p)。重复上述过程直至没有回路形成,从而得出路径优化;⑥确定路径优化的最优方案。重复上述的合并过程,得出多种路径优化的方案并进行对比,得出最优方案。 本文首先不考虑配送车辆的载重量以及其他约束条件,假定该餐厅仅有一辆配送车辆的情况下想要实现对所有顾客需求点进行配送,在该情况下设计相应的路径优化方案。 根据案例背景建立模型如下: 对上述模型用EXCEL进行规划求解,求解约束设置如下,并得到最终的求解结果为配送路径为0-2-1-8-3-7-6-5-9,所需要的配送总时间为71min,载重量36份,所需时间较长,无法及时满足顾客的所有需求。 图3 EXCEL求解结果 本小节主要讨论多配送车辆且有载重约束的优化方案,通过案例背景已知配送车辆载重上限为15,也就是说每辆配送车辆最多职能一次性装载15份外卖,如果该配送车辆路径上的外卖需求量超过了15则需要另一辆配送车辆进行配送。本小节主要通过节约算法对配送车辆的路径进行规划,并且求解出在该需求背景下该餐厅需要配置多少辆配送车辆。 约值按照降序的方式进行排序,具体如下所示。 首先在表2的基础上计算连接各需求点的节约值并对这些节 表4 各需求点连线节约值 表5 节约值排序 由该表可以看出,一些连接点的节约值为负数,即对这两各需求点进行连接不但不会减少配送时间还会增加配送时间,这显然是不可行的,因此对节约值为负数的连接点可以直接不予考虑。 按照节约值的大小,即上表的顺序依次判断各连接点是否满足节约算法的连接规则,即是否在同一条线路上,是否与基点,即餐厅0相邻,得到最终的配送路径规划如下所示。 图4 多车辆考虑载重情况下的配送路径优化图 根据配送路径优化图可以得到在该配送方式下需要3辆配送车辆同时配送,配送路线分别为0-2-1-8-7-0,0-3-6-0,0-4-9-5-0,所需时间分别为45,23,26,由于同时配送所以所需时间为45,各配送车俩的载重量均为50%以上,具体数值如下表所示。 表6 多车辆考虑载重情况下配送路径优化结果 除了考虑载重量与车辆这些硬件设备,即商家所必须的设备外,不可忽视的是顾客满意度,而顾客满意度衡量的指标即为是否在规定的配送时间内收到外卖。在实际生活中我们常常可以设置外卖具体在某一规定时间送达,迟到或者早到都是不可以的,正如案例中所给出的顾客需求一般,于是在4.2的基础上本小节主要考虑了时间窗的限定利用节约算法再次进行求解。虽然考虑了时间窗,但是节约算法的本质是没有改变的,只是在原来的基础上除了载重这一限定条件外计算时间,只有在时间窗内才可以连接两需求点,并且由于考虑了时间窗因素此时在同一路径上的配送具有先后顺序,不可颠倒,节约值与排序同4.2,这里不再赘述。 根据案例所给出的数据,本文假定在每一个配送点的逗留时间为2min,即配送员将外卖送至地点后联系顾客等待顾客收取外卖需要2min的时间。11:30为初始配送时间0,依次类推,在初始时刻,当配送车辆从餐厅到往任务点i时,若则若t0i=ETi, 取Si=ETi其中ETi表示该需求点的最早可接受外卖时间,LTi表 示该需求点最晚可接受外卖的时间,Si为外卖到达的时间,根据此规则可以得到初始情况如下。 表7 各配送点的特征与要求 在该表的基础上通过节约算法进行计算,计算过程以及结果如下所示。 图5 节约算法计算流程图 图6 多配送车辆考虑载重与时间窗的配送路径 根据配送路径的优化结果可以得到在该种配送方式下以共需要5辆配送车辆,才能满足配送需求,使得各个配送点都不会出现提前或者推迟的情况,配送路线分别为7→8,2→4→9,1→6,3,5,配送时间分别为33,25,38,7,25,由于各配送线路同时配送故整体配送完成需要时间为38min,然而为了满足时间窗,在规定时间内送达,单跳线路的整体载重率不高,载重存在浪费现象,具体配送路径设计情况如下表。 表8 多配送车辆考虑载重与时间窗的配送路径优化结果 通过4.1~4.3三种情况下的配送方案对比可以直观看到各方案下所需要的配送时间、配送路径、载重量等数据如下表所示。 表9 方案对比表 从上表中可以清晰看出,方案1配送路径最少,所需时间最多,所需车辆最少,方案二平均载重率最高,方案三配送路径数最多,平均载重率最低,所需车辆数最多。 由此可得,为了满足时间窗的需求,使得所有的顾客都可以在期望的时间内收到外卖会使得载重率与车辆数增多,即会使得经营成本增加,而只使用一辆配送车辆是不可行的,其所需要的时间等相关特征值均不具有优势,如果不考虑时间窗多配送车辆的载重率与所需车辆数都较为理想。 从方案对比中也可以看出物流问题中的效益背反理论,为了给顾客提供更加高质量的需求就必须要浪费一定的车辆资源,这是一个此消彼长的过程,关键在于商家该怎样决策,从长远的角度看顾客的满意度是企业是否能够经营下去的关键,适当的资源浪费是合理的,故方案3最为合理。 本文主要以实际案例为背景,通过TSP求解算法与节约算法从三个方面提出了不同的外卖配送路径的具体优化方案,并进行了对比,从而分析不同约束条件下的不同配送路径优化方案,并从实际的角度简要分析了方案的可行性,为该餐厅提出了可行的配送指导方案,提高了该餐厅的市场竞争力与顾客服务水平,对相关的外卖行业也可以进行进一步的引申应用。
4 优化方案
4.1 单配送车辆不考虑载重优化方案

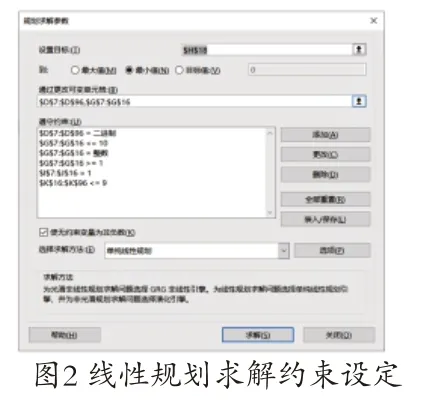
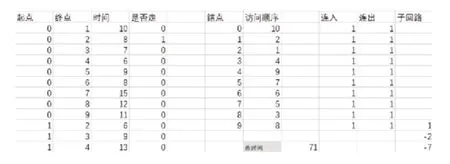
4.2 多配送车辆考虑载重优化方案




4.3 多配送车辆考虑载重与时间窗的优化方案

4.4 方案对比

5 结语

