超弹性本构模型对UHMWPE的适用性

朱凯辉 陈欢

摘  要：超高分子量聚乙烯（UHMWPE）是高分子聚合物的一种，在使用过程中既有弹性的一面，也有非弹性的一面。以弹性为基础，从线性和非线性角度出发，通过单轴拉伸实验获得UHMWPE的力学性能曲线，对比实验曲线和本构模型拟合曲线，讨论了Ogden超弹性模型对UHMWPE力学性能拟合的适用性。结果表明Ogden超弹性本构模型可以很好地拟合实验结果，为以后采用有限元分析方法研究UHMWPE机械性能响应提供理论基础。

关键词：UHMWPE  单轴拉伸实验  力学性能  超弹性本构模型

中图分类号：TU13                              文獻标识码：A                    文章编号：1674-098X（2021）02（b）-0067-06

Applicability of Superelastic Constitutive Models to UHMWPE

ZHU Kaihui*  CHEN Huan

（School of Mechanical Engineering， Yangtze University， Jingzhou， Hubei Province， 434023 China）

Abstract： Ultra high molecular weight polyethylene （UHMWPE） is a kind of high polymer， which has both elastic side and inelastic side in use.Based on the elasticity， the uniaxial tensile test was used to obtain the mechanical property curve of UHMWPE from the linear and nonlinear angles. By comparing the experimental curve and constitutive model fitting curve， the applicability of Ogden superelastic model to UHMWPE mechanical property fitting was discussed.The results show that the Ogden hyperelastic constitutive model can fit the experimental results well， which provides a theoretical basis for the future finite element analysis method to study the mechanical property response of UHMWPE.

Key Words： UHMWPE; Uniaxial tensile experiment; Mechanical properties; Hyperelastic constitutive model

超高分子量聚乙烯作为一种新开发的工程塑料，具有优异的机械性能，不吸水、尺寸稳定、耐磨损耐腐蚀，同时还具有无毒无害、无污染、能够回收利用的特点，是一种对于环境和人体友好的绿色材料，在食品、饮料、医疗卫生等行业具有广阔的应用前景[1]。随着UHMWPE材料应用得越来越广泛，其力学性能的表征则越发重要，采用商业有限元模拟的方法更加灵活，可以选取从简单到复杂的本构模型且可以对更加复杂的材料几何形状进行模拟，有限元以其低廉的计算成本成为验证材料模型和预测机械响应的实用工具[2]，任何有限元分析都需要适当的几何形状、加载条件和本构模型的输入，合适的本构模型能使有限元结果更加准确。

陆松[3]等采用超弹性的Arruda-Boyce模型与粘弹性力学模型相结合，模拟分析了超高分子量聚乙烯齿轮的应力分布、变形和承载能力;陈开卷[4]等人基于实验结果建立了循环本构模型描述了不同结晶度对超高分子量聚乙烯单轴和多轴棘轮行为的影响，结果表明所提出的模型能够合理的预测不同结晶度超高分子量聚乙烯的单轴和多轴棘轮行为;穆磊金[5]利用Sherwood-Frost本构模型描述了PC、PMMA、PA、PE四种聚合物的准静态压缩和动态压缩力学性能，并结合实验数据拟合得到模型材料参数，通过实验曲线和模型预测曲线对比得出所获得本构模型参数是正确的;马塞尔[6]等人利用Sherwood-Frost本构模型研究了PE-HD单轴拉伸力学行为，得出Sherwood-Frost本构模型能较好的描述PE-HD的力学特性;齐正磐[7]研究了在循环加载条件下高密度聚乙烯的本构模型和聚乙烯的失效机理与疲劳行为;徐立志[8]等建立了在不同压缩率下聚乙烯材料的压缩力学性能;雷鹏[9]对聚乙烯拉伸应变速率的本构方程进行了改进并对其进行应用。然而，以上研究大都没有考虑模型在不同分子量UHMWPE之间的适用性，对于适合描述UHMWPE在变形较大、应变率范围较宽时本构模型的研究较少。

本文选取超高分子量聚乙烯（UHMWPE）为研究对象，通过单轴拉伸实验得到材料的应力应变曲线，采用不同本构模型对UHMWPE不同阶段的拉伸力学行为进行描述，通过模型预测曲线与实验曲线的对比，验证两本构模型在不同应变阶段下的适用性。

1  超高分子量聚乙烯（UHMWPE）单轴拉伸实验

1.1 试样制备

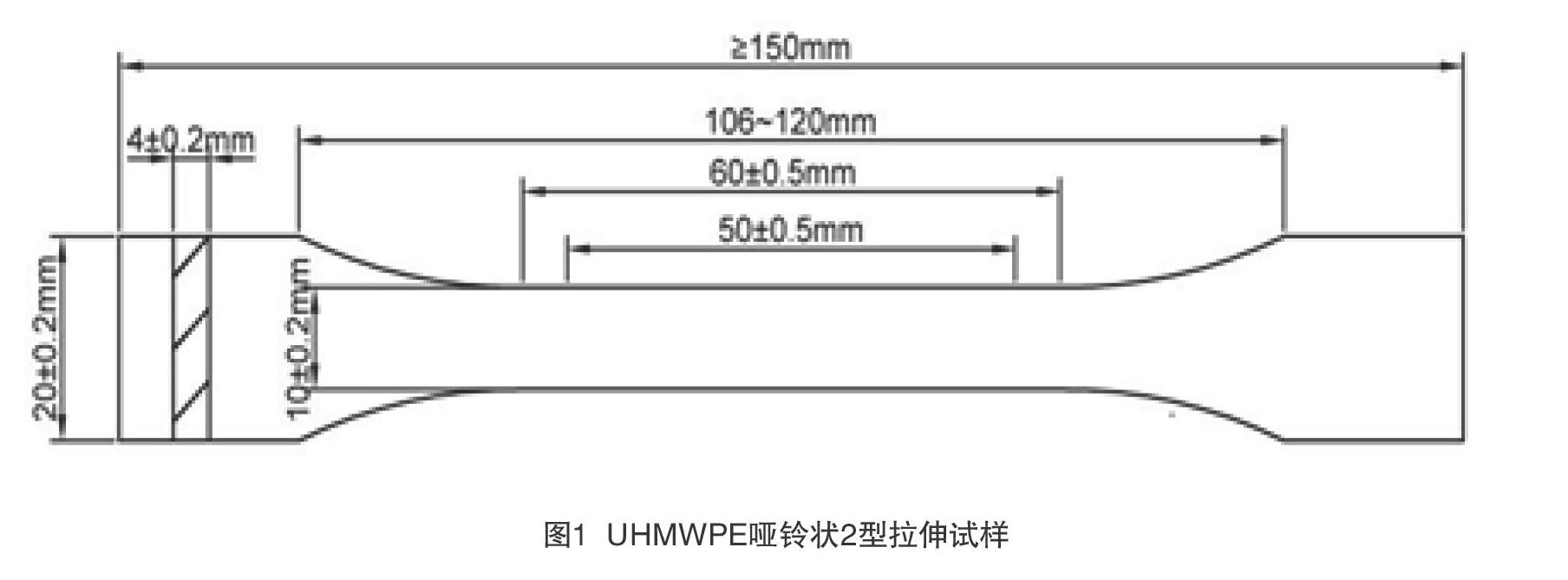
实验所用的材料为UHMWPE，分子量分别为300、600、920万三种，试样加工根据GB/T1040-2006，选择哑铃状2型试样：狭窄部分的标准宽度为10.00±0.2 “mm”，长度60.00±0.5 “mm”，具体尺寸见图1。试样直接从UHMWPE棒料上切下通过机加工加工成哑铃状，试样加工完成后静置48“h”以消除残余应力。

1.2 实验过程

在室温条件下，使用QJ211型电子万能试验机对UHMWPE拉伸试样在50、200“mm/min”二种拉伸速率下进行恒速单轴拉伸试验，对应的应变率分别为0.01667、0.06666s-1，在整个试验过程中，连续监测试样长度和力的变化。如果试样在狭小平行部分之外发生断裂，则该试验结果应予以舍弃，并应另取一试样重复试验，为了避免实验误差每个拉伸速率下重复试验5次取其平均值。

1.3 实验结果

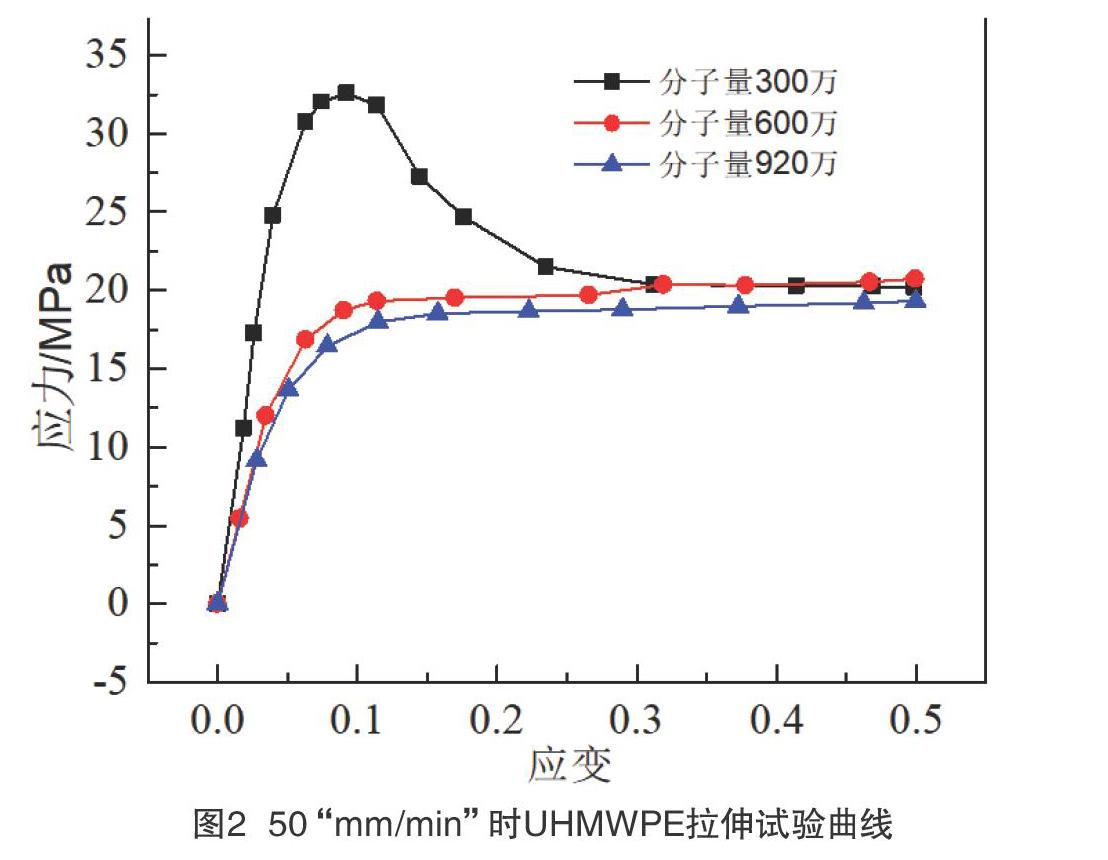
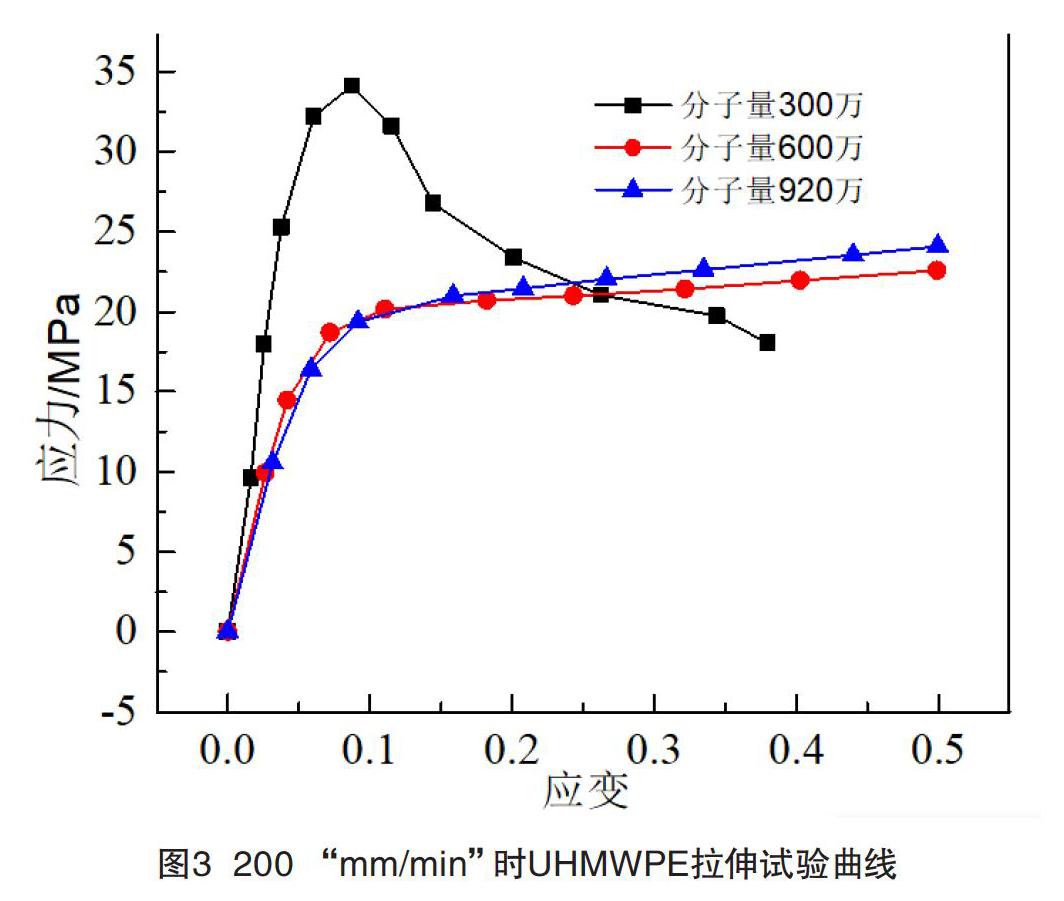
由实验得到不同拉伸速率（应变率）下的单轴拉伸应力应变曲线，如图2、3所示。可以发现在不同拉伸速率下，随着应变逐渐增大UHMWPE的单轴拉伸应力先经历一段线性上升，达到屈服极限后再进入塑性流动，总体趋势为：UHMWPE分子量越大，结晶度下降，减弱链段之间相互作用易产生拉伸屈服，所以分子量越大其屈服应力越小，模量越低，表现为低模量低屈服强度;拉伸速率增大，材料的屈服应力增大，表现出应变率强化效应。

2  UHMWPE的超弹性本构模型

2.1 超弹性模型

线性弹性的延伸就是超弹性[10]，超弹性模型是一组应变能密度只取决于当前材料的变形状态（而不取决于整个变形的历史）的一类模型的总称，这类材料模型是以非线性弹性响应为特征，不考虑材料的屈服、粘塑性和时间依赖性。

UHMWPE作为一种高粘弹性材料在承受载荷时，其变形不但与应力相关而且和加载时间有关，体现的是一种非线性关系，这一点在大变形时表现的更加明显。因此在研究UHMWPE的力学行为时，应尽量采用非线性处理方法才能获得更加精确的结果，对于非线性粘弹性理论，研究者们从微观到宏观、从静态到动态都提出一系列的力学模型，这些模型要么推导过于复杂，要么就是模型所需要的参数不易通过试验获得。目前国内外学者比较认可的是采用超弹性考虑其非线性[11]，美国HKS公司开发的ABAQUS有限元软件在处理非线性粘弹性问题时，对非线性弹性应变部分采用大变形的超弹性力学模型;文献[11]中提到采用Ogden超弹性模型考虑非线性，Ogden超弹性模型是用来描述大变形、大位移材料的最佳模型。由于在加载方式单一、加载速率恒定时，是不可区分UHMWPE的非线性弹性和粘弹性行为的，故本文选取目前最为常用的超弹性模型为基于维象法的Ogden模型、M-R模型和基于热力统计法的Arruda-Boyce的八链模         型[12-13]，超弹性模型常用于不可压缩橡胶的建模，模型参数也可直接通过商业有限元软件ABAQUS拟合得到。

2.1.1 超弹性本构模型的选择

首先选用分子量920万UHMWPE拉伸速率50 “mm/min”为例，分别采用以上三种超弹性模型通过有限元软件ABAQUS进行数据拟合，各模型应力应变曲线如图5所示。

由图4可知在应变小于0.5的情况下Ogden模型可以准确的描述UHMWPE的单轴拉伸非线性力学行为，误差非常小，而采用M-R模型和Arruda-Boyce八链模型的拟合曲线与实验曲线均有较大的误差，因此本文选用Ogden模型，其表达式为[14]：

（1）

式中J-变形体积与未变形体积之比;λ1、λ2、λ3三个方向的主伸长率;αi、μi-材料参数;Di-表示材料是否可压缩，其中，不可压缩材料Di=0。

2.1.2 Ogden模型拟合曲线和实验曲线对比

采用Ogden模型分别对不同分子量和拉伸速率下UHMWPE单轴拉伸实验数据进行拟合，拟合结果如图5、6、7所示。

由图5、6、7所示结果可知Ogden超弹性本构模型能够很好的描述以上三种分子量和二种拉伸速率下的UHMWPE非线性力学性能，可以看到只有分子量300万UHMWPE在拉伸速率为50“mm/min”时的试验曲线与预测数据曲线误差稍大;表1给出了在不同拉伸速率下UHMWPE试验曲线与预测数据曲线的拟合优度，通过对比表1中的拟合优度可知：当拉伸速率为50“mm/min”、200“mm/min”時，拟合优度均表现为UHMWPE分子量越高拟合优度越高。分析原因为：UHMWPE是典型的结晶聚合物，拉伸屈服应力主要由结晶度变化决定的，分子量越高结晶度减弱，在单轴拉伸状态下的非线性阶段表现为低模量、低屈服应力的性能，因此使用Ogden模型拟合时拟合优度更高。

由以上分析可得出结论：对于UHMWPE单轴拉伸非线性阶段可以采用Ogden超弹性模型来描述其力学性能，且分子量越高其拟合效果越好，Ogden超弹性本构模型是一种简单地、易于理解、易与计算的模型并且能较好的描述UHMWPE非线性阶段的单轴拉伸力学行为，对于实验数据较少时具有重要的实际意义。

3  结论

（1）UHMWPE材料的分子量越大，屈服强度越低;UHMWPE的屈服应力随拉伸速率（应变率）的增大而提高，表现出明显的应变率强化效应。

（2）对于超弹性模型的探讨我们可知在UHMWPE单轴拉伸非线性阶段可以采用Ogden超弹性模型来描述其力学性能，且分子量越高拟合效果越好，对于实验数据较少时具有重要的实际意义。

参考文献

[1] 陆松，孟惠荣.几种适合超高分子量聚乙烯的力学模型[J].煤矿机械，2003（10）：31-33.

[2] Bowden A E， Oneida E， Bergstr·m J. Chapter 35 – Computer Modeling and Simulation of UHMWPE[J]. Uhmwpe Biomaterials Handbook，2009：519-532.

[3] 陸松，孟惠荣.基于粘弹性超高分子量聚乙烯齿轮有限元分析[J].辽宁工程技术大学学报：自然科学版，2004，5（23）：589-591.

[4] 陈开卷，康国政.结晶度对超高分子量聚乙烯棘轮行为的影响：实验和本构模型[C].2018年全国固体力学学术会议论文集.

[5] 穆磊金.典型聚合物材料应变率相关本构模型研究[D].绵阳：西南科技大学，2017.

[6] 马赛尔，许进升，童心，等.高密度聚乙烯单轴拉伸力学性能及本构关系研究[J].中国塑料，2016（4）：88-92.

[7] 齐正磐.循环加载下高密度聚乙烯的本构模型，失效机理和疲劳行为[D].重庆：重庆大学，2019.

[8] 徐立志，高光发，赵真，等.不同应变率下聚乙烯材料的压缩力学性能[J].爆炸与冲击，2019，39（1）：58-65.

[9] 雷鹏.聚乙烯拉伸应变速率的本构方程改进及运用[J].包装工程，2019，40（13）：110-115.

[10] Ogden RW.Non-linear elastic deformations. Mineola， NY： Dover publications;1997.

[11] Mullerschon H，Dangel A，Karjan N，Hummel A.LS-DYNA Anwenderforum，Bamberg，2004.

[12] 李晓芳，杨晓翔.橡胶材料的超弹性本构模型[J].弹性体，2005（1）：52-60.

[13] 陈家照，黄闽翔，王学仁，等.几种典型的橡胶材料本构模型及其适用性[J].材料导报：纳米与新材料专辑， 2015（29）：118-120.

[14] Ogden R W. Large Deformation Isotropic Elasticity-On the Correlation of Theory and Experiment for Incompressible Rubberlike Solids[J]. Proceedings of the Royal Society of London， 1972，326（1567）：565-584.