政府监管下智慧矿山建设系统演化仿真分析
易 涛,栗继祖
(太原理工大学经济管理学院,山西 太原 030024)
根据总体设计,分步实施的原则,煤炭企业矿山建设分为三个阶段,分别是数字矿山、智慧矿山和无人矿山[1]。智慧矿山又称智能矿山和“物联网”矿山,是以深度互联、高度共享、透彻感知、智能服务和可视化展现为基本特征,旨在通过对信息系统采集到的数据进行深度挖掘分析,实现煤炭企业生产经营管理的智能决策[2]。智慧矿山以安全生产为首要原则、减员增效为主要目的,其建设状况直接影响到煤炭产业生产管理变革的推进。智慧矿山建设不仅是煤炭企业发展规划中的重要一步,也是政府构建安全高效煤炭工业生态中的关键一环。因此,以政府为主体制定合理政策推动煤炭企业智慧矿山建设,对避免煤炭企业发展掉队、保障煤矿生产安全、促进煤炭生产管理信息化和推动煤炭产业转型升级具有重要意义。
目前,国内外学者围绕智慧矿山理论及发展路径展开了丰富的研究。智慧矿山理论研究拓宽和加深了学界对智慧矿山的认识,学者谭章禄等[3]指出智慧矿山是在数字矿山和感知矿山基础上,应用云计算、人工智能等科学技术发展的矿山信息化建设新阶段,而完整的理论体系是智慧矿山落地的基础;吕鹏飞等[4]认为智慧矿山是基于物联网、人工智能等先进技术的完整智慧体系,可以实现矿山生产经营管理各环节的最优调控;卢新明等[5]则认为智慧矿山是建立在矿山数字化基础上,能够完成矿山企业所有信息的精准适时采集、网络化传输、规范化集成、可视化展现、自动化操作和智能化服务的数字化智慧体;李小四等[6]认为智慧矿山建设的真正内涵是能在矿山物联网上提供各种各样矿山所需要的智慧化服务。此外,部分学者以理论框架为基础,对智慧矿山发展路径展开了研究。LYNAS等[7]分析了智慧矿山建设过程中产生的技术变革及其不规范发展将带来的潜在问题,并指出了智慧矿山的发展方向;RALSTON等[8]则从技术的角度讨论了系统兼容性和开放通信标准对促进企业智慧矿山建设的意义,强调将智慧矿山技术从独立、封闭的系统转换为开放、共享的技术体系;徐静等[9]从价值链的角度研究分析了矿山物联化和智能化设计的关键技术及其实现路径,构建了符合中国实际的智慧矿山理论框架和方法体系;王莉[10]则从数字矿山、物联网和云计算的角度构建了智慧矿山蓝图,并指出政府和矿山企业的通力合作是实现矿山智能化的必要条件之一;王国法等[11-13]基于当前的数字矿山发展现状,为中国智慧矿山建设提出了情景目标和发展路径。由文献分析可知,学者们对智慧矿山的技术体系、发展路径以及建设目标等方面进行了深入研究,为中国智慧矿山发展建设奠定了坚实基础,但是同时也存在一定的局限性:已有研究主要集中于智慧矿山的理论与发展路径问题,而较少考虑区域内煤炭企业的智慧矿山建设问题;有学者指出政府参与是智慧矿山建设的重要因素,但鲜有学者考虑到政府和煤炭企业之间的决策博弈问题;在煤炭企业追求生存和变革的过程中地方政府推动智慧矿山建设,二者的策略交互受何种因素影响。
基于此,本文将采用演化博弈与系统动力学(system dynamics,SD)仿真的综合研究方法,构建起以智慧矿山建设为焦点,以地方政府和煤炭企业为主体的博弈模型,从而对政企双方的策略选择进行演化稳定分析,在剖析政企双方策略互动机制的同时,改变政府的静态奖惩措施,提出动态的奖惩方案。最后通过演化博弈均衡分析与SD仿真揭示动态奖惩方案如何抑制原系统的振荡特性,从而得到演化稳定策略(evolutionary stability strategy,ESS)。本文建立的演化博弈与SD模型为分析政府和煤炭企业智慧矿山建设的动态博弈过程提供了一个理论和实证相结合的仿真平台,对于政府调动煤炭企业群体智慧矿山建设积极性,保障煤炭行业健康可持续发展具有现实意义。
1 演化博弈模型假设及构建
1.1 演化博弈模型假设
1.1.1 博弈中的参与者
现假定演化博弈模型中只包括政府和煤炭企业两个利益主体,博弈双方都是有限理性。其中,政府是指由煤炭工业局、经济和信息化委员会及相关部门抽调成员后组成的监管部门,该部门有能力确认煤炭企业智慧矿山建设的合规性与先进性;煤炭企业是指仍处于机械矿山或数字矿山阶段需要进行智慧矿山建设的煤炭生产企业,其井下生产需要较多的作业人员,智慧矿山建设需要煤炭企业短期内在信息系统升级方面投入资金。
1.1.2 政府和煤炭企业的行为策略
假设政府以概率α(0≤α≤1)对辖区内煤炭企业的智慧矿山建设进行监管,Cg为政府每次监管辖区内煤炭企业所要耗费的成本,比如巡查辖区内煤炭企业智慧矿山建设时所耗费的人力资源、物力资源和财力资源。同时,政府将在监管过程中将对煤炭企业采取激励或惩罚措施,如果监管过程中发现辖区内煤炭企业智慧矿山建设情况良好,则政府将给予一定的补贴Am;反之,若政府监管过程中发现煤炭企业在智慧矿山建设过程中出现消极应付和维持现状的情况,则将对煤炭企业予以惩罚Fm。煤炭企业完成智慧矿山建设,政府将因煤炭企业减少危险岗位人员数量、提高区域煤炭生产安全性等获得间接效益Bg;若煤炭企业选择维持现状生产,则政府将为煤炭企业生产监管及保障等方面多支付政府成本Lg。
假设煤炭企业以概率β(0≤β≤1)进行智慧矿山建设,煤炭企业选择智慧矿山建设过程中会产生设备购入、矿井停工和员工培训等直接投入成本Cm,但会带来节约人力成本、减少安全事故及提升生产效率等预期效益Bm。煤炭企业选择维持现状生产时,可以不因智慧矿山建设停工影响继续生产获得正常生产收益Pm。根据上述分析和假设,构建政府、煤炭企业之间关于建设智慧矿山的关系机理图,如图1所示。同时政府、煤炭企业双方之间的收益矩阵见表1。

图1 政府和煤炭企业智慧矿山建设的关系机理图Fig.1 Relationship mechanism diagram of smart mines construction betweengovernment and coal enterprises

表1 政府和煤炭企业双方博弈的收益矩阵Table 1 Return matrix of the game between governmentand coal enterprise
1.2 演化博弈模型构建
根据假设可知,政府的策略选择为{监管,不监管},煤炭企业的策略选择为{智慧矿山建设,维持现状};令每个博弈方的收益函数为:U=(Ui,U1-i)(i=α,β),根据收益矩阵可以得到博弈双方的期望收益Eg与Em,进而得到双方演化博弈的复制动态方程组[14],见式(1)~式(3)。
Eg=αUα+(1-α)U1-α=αβ(-Am-Fm)+
α(-Cg+Fm)+β(Bg+Lg)-Lg
(1)
Em=βUβ+(1-β)U1-β=αβ(Am+Fm)-
αFm+β(-Cm+Bm-Pm)+Pm
(2)

(3)
2 政府和煤炭企业间演化博弈模型稳定性分析
2.1 政府单方策略演化稳定性分析
由式(3)可知,政府策略的复制动态方程为S(α)=α(1-α)(-βAm-βFm-Cg+Fm),对S(α)求导得式(4)。
(1-2α)(-βAm-βFm-Cg+Fm)
(4)


表2 政府单方面策略演化稳定性分析Table 2 Stability analysis of the evolution of government’s unilateral strategy
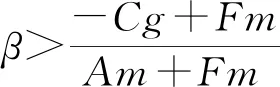

图2 政府的复制动态相位图Fig.2 Replication dynamic phase diagrams of government
2.2 煤炭企业单方策略演化稳定性分析
由式(3)可知,煤炭企业策略的复制动态方程为S(β)=β(1-β)(αAm-Cm+Bm+αFm-Pm),对其求导得式(5)。
(1-2β)(αAm-Cm+Bm+αFm-Pm)
(5)
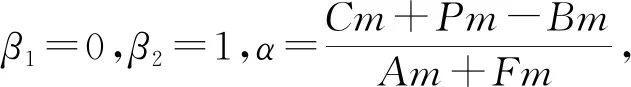

表3 煤炭企业单方面策略演化稳定性分析Table 3 Stability analysis of the evolution of coal enterprises’ unilateral strategy


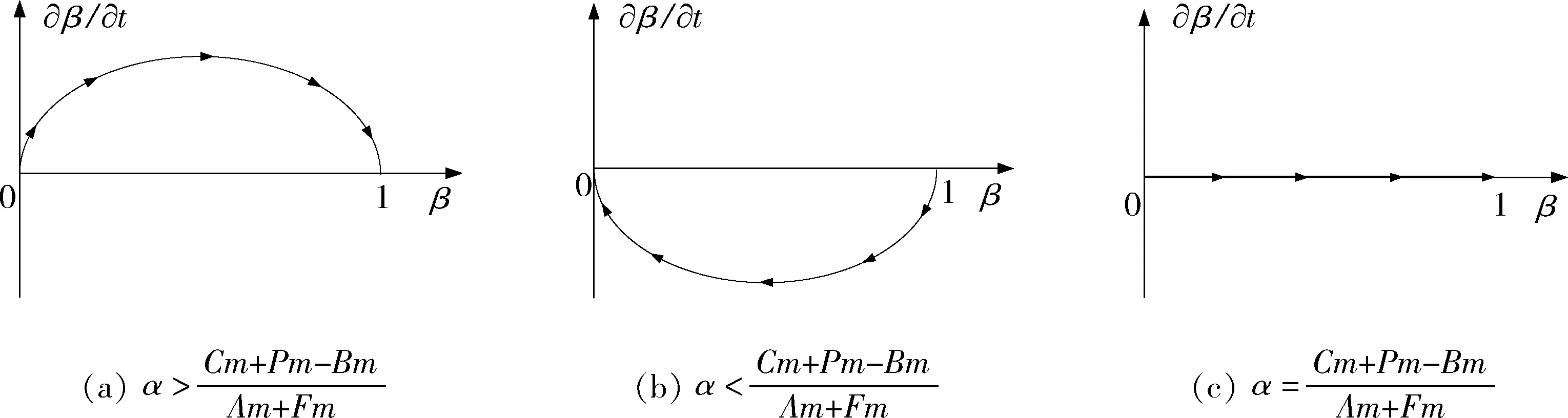
图3 煤炭企业的复制动态相位图Fig.3 Replication dynamic phase diagrams of coal enterprise
2.3 政府和煤炭企业混合策略的演化稳定性分析
由上述分析可知,政府和煤炭企业单方面的策略选择都具有三种不同的ESS。 但从实际出发,煤炭企业进行智慧矿山建设所投入的实际成本与维持现状的生产收益之和会高于改造建设所带来的收益,这主要源于智慧矿山建设所产生的智慧生产系统改造、智慧职业健康与安全系统升级以及智慧技术支持与后勤保障系统建设的高昂成本。同时政府的监管成本很难超过政府制定的罚金,单方面的要求煤炭企业主动开展智慧矿山建设的几率较低,所以需要着重讨论政府和煤炭企业双方混合策略的稳定性。
演化稳定均衡点的稳定性可由该系统的雅可比矩阵的稳定性分析得到,则根据复制动态方程(3),得出雅克比矩阵见式(6)。


表4 Nash均衡点稳定性分析Table 4 Stability analysis of Nash equilibrium points

显然,均衡点(X0,Y0)对应的特征根λ1,2为一对纯虚根。 因此,(X0,Y0)是稳定的平衡点,但并不是ESS,其系统演化轨迹是围着中心点(X0,Y0)循环运动的闭轨线环[16],此情况反应了政府监管下煤炭企业采取智慧矿山建设的过程具有反复性、长期性和艰巨性。
3 基于演化博弈的SD仿真模型
3.1 SD模型设置与初值确定
根据以上演化博弈模型分析,利用Vensim PLE软件建立政府监督下煤炭企业智慧矿山建设的演化博弈SD模型,该模型包含2个状态变量、2个速率变量、8个外部变量、6个辅助变量以及2个影子变量,如图4所示。设置SD模型初始值为:仿真起始时间INITIAL TIME=0,仿真结束时间FINAL TIME=100,本仿真中的数据为模拟数据,Time泛指一般时间单位。同时根据山西焦煤集团晋兴能源公司斜沟矿井智慧矿山系统建设案例部分实际数据和仿真模拟的需要设定模型初始值,见表5。

表5 政府和煤炭企业SD模型的变量含义及初值Table 5 Variable meanings and initial values ofSD model for government and coal enterprise

图4 政府和煤炭企业演化博弈的SD模型Fig.4 SD model of evolutionary game between government and coal enterprise
3.2 SD初始仿真分析


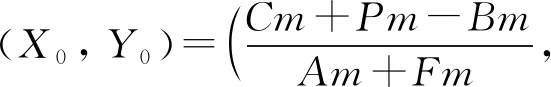
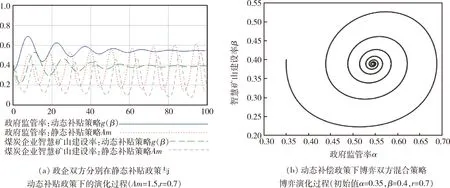
图5(b)给出了政企双方均以Initial3(α,β)=(0.35,0.4)为初始概率下系统的博弈演化趋势曲线。结果显示,政企双方参与的智慧矿山建设博弈系统演化过程是一个围绕起始点进行周期运动的闭轨线环,这表明了在智慧矿山建设的演化博弈中政府和煤炭企业的博弈过程表现出一种周期行为模式。因此,为使博弈双方混合策略演化过程有效收敛,需进一步调整方案研究。

图5 政府和煤炭企业系统演化过程Fig.5 System evolution process of government and coal enterprise
4 政府动态奖惩政策混合博弈与仿真
政府对煤炭企业智慧矿山建设补贴和惩罚的合理程度不仅会影响政府自身的监管积极性,还会影响煤炭企业智慧矿山建设的投入积极性。相关研究表明[17-19],政府对煤炭企业实施动态惩罚或奖励机制,可以显著改善政府和煤炭企业演化博弈均衡点的稳定性。因此,在借鉴已有研究思路和成果的基础上,根据智慧矿山建设实际状况,构建起动态惩罚模型和动态奖励模型,并对其纳什均衡点稳定性进行理论与SD仿真分析。
4.1 政府动态惩罚政策博弈与仿真
煤炭企业传统矿山生产比例越高,矿山生产的潜在风险性便越高。而政府对煤炭企业采取动态惩罚政策是为了降低传统矿山生产比例,提高煤炭企业智慧矿山建设率。在政府推动区域内煤炭企业智慧矿山建设初期,因辖区内煤炭企业智慧矿山建设完成率偏低,矿山生产所造成的负外部效应较高,政府会提高惩戒力度督促煤炭企业开展智慧矿山建设。随着煤炭企业智慧矿山建设比例提高,煤炭企业生产所造成的负外部效应也随之降低,政府会相应降低对煤炭企业维持现状的惩罚力度。据此,假设当政府实行监管策略且煤炭企业选择维持现状时,令政府对煤炭企业收取的罚没金额由固定常数Fm变为h(β)=(1-β)f,且f>Am+Cg,其中,f为政府的最高惩罚力度,表示政府最高惩罚力度以政府补贴与监管成本之和为下限。
4.1.1 动态惩罚策略系统稳定性分析
将h(β)=(1-β)f代替式(3)中的Fm得到系统复制动态方程组,见式(7)。

(7)

从而解得:

4.1.2 动态惩罚政策下系统博弈均衡点分析
已知0

(9)
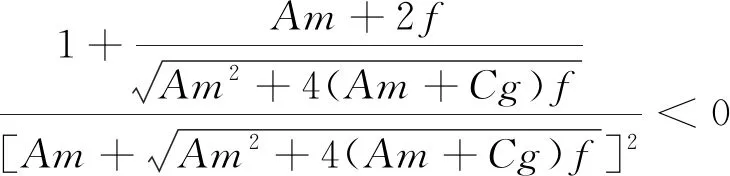
(10)

(11)
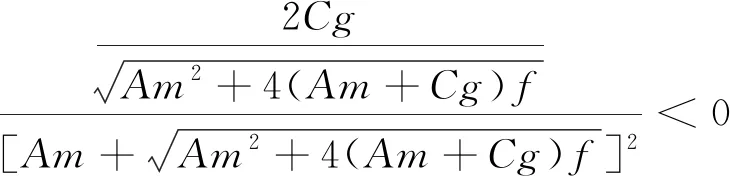
(12)
同理,对β*的各个参数分别求导,得到式(13)~式(15)。
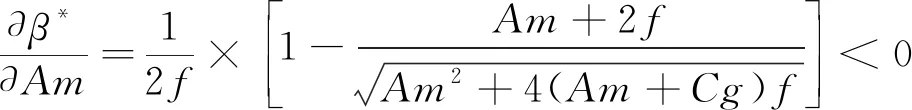
(13)
(14)
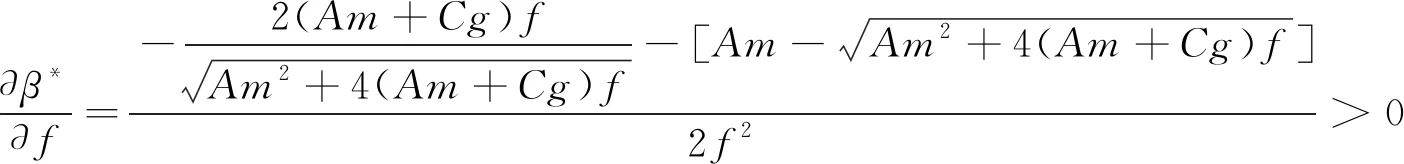
(15)
因此,政府补贴力度Am、政府监管成本Cg以及最高惩罚力度f会同时影响α*与β*的大小。提高政府补贴力度Am会使α*与β*同时减小;减小政府监管成本Cg能使α*和β*同时增大;而当政府最高惩罚力度f增大时,α*减小,而β*增大,表明政府在动态惩罚措施下可以提高最高惩罚力度f使自身监管概率α*降低并提高煤炭企业的智慧矿山建设率β*。同时,对政府而言,帮助煤炭企业降低智慧矿山建设成本Cm、降低其维持现状的生产收益Pm,与提升煤炭企业智慧矿山建设效益Bm都可以有效降低政府监管概率。
4.1.3 动态惩罚政策SD仿真分析
使用Vensim PLE软件分别仿真静态惩罚策略和动态惩罚策略下政府和煤炭企业策略的演化过程,如图6(a)所示。由图6(a)可知,以相同的初始值α=0.35,β=0.4,在静态惩罚政策下,政府和煤炭企业的策略选择不断波动,振幅随着博弈次数与时间的增加有扩大之势,且政府选择监管率普遍高于煤炭企业选择智慧矿山建设率;而在动态惩罚政策下,政府和煤炭企业的策略波动随着时间与博弈次数的增加而逐渐趋于稳定,且煤炭企业选择智慧矿山建设率普遍高于政府选择监管率。这表明,政府动态惩罚策略有利于提高煤炭企业的智慧矿山建设率,且使博弈双方较快达到系统的演化稳定均衡点。
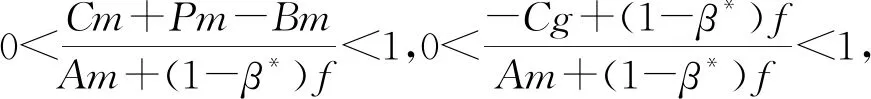

图6 政府和煤炭企业在惩罚政策下的演化过程Fig.6 Evolution process of government and coal enterprise under punishment policy
4.2 政府动态补贴政策博弈与仿真
政府采用补贴激励策略是为了促进智慧矿山在煤炭企业的建设应用。在此策略的实施初期,进行智慧矿山建设的煤炭企业比例相对较低时,政府为降低矿山生产的潜在风险,提高区域内煤炭企业矿山生产的安全性,政府会具有较强的意愿去激励煤炭企业,所以会给实施智慧矿山建设的煤炭企业提供较高的补贴;反之,当选择智慧矿山建设的煤炭企业比例提升时,辖区内煤炭企业生产的潜在风险便会大幅降低,政府对煤炭企业的补贴意愿将随之降低,从而对实施智慧矿山建设的煤炭企业提供较低的补贴。据此,假设政府的补贴金额与煤炭企业智慧矿山建设率成反比,即当政府选择监管且煤炭企业选择智慧矿山建设时,令煤炭企业智慧矿山建设得到政府的奖励补贴费用由固定值Am变为函数g(β)=(1-β)r,并且0 4.2.1 动态补贴政策系统博弈稳定性分析 根据上述分析,将g(β)=(1-β)r代替式(3)中的Am得系统复制动态方程组见式(16)。 (16) (17) 从而解得: 4.2.2 动态补贴政策下系统博弈均衡点分析 已知0 (18) (19) (20) (21) 其次对β**各个参数分别求导,得到式(22)。 (22) 由此可得,政府的补贴上限r、政府对煤炭企业的惩罚Fm以及政府的监管成本Cg会同时影响α**和β**的大小。提高补贴上限r时,α**与β**会同时减小;增大惩罚Fm时,α**会减小而β**会增大;减少Cg时,α**和β**同时增大。另外,当煤炭企业智慧矿山建设成本Cm增加、维持现状的生产收益Pm增加如煤炭价格短期内大幅上涨,以及煤炭企业智慧矿山建设收益Bm降低时,会造成政府监管概率α**的上升而增加政府工作量。 4.2.3 政府动态补贴政策SD仿真分析 利用SD模型分别对静态补贴政策和动态补贴政策下的政府和煤炭企业策略的演化过程进行仿真,如图7(a)所示。由图7(a)可知,以相同的初始值α=0.35,β=0.4为前提,在静态补贴政策下,政府和煤炭企业策略选择反复波动,并且随着时间与博弈次数的增加波动幅度有扩大趋势;但在动态补贴政策下,随着时间和博弈次数的增加,政府和煤炭企业的策略选择逐渐趋于稳定,波动也得到显著的抑制。这表明相对于静态补贴政策,政府的动态补贴政策有利于政企双方选择的混合策略达到演化稳定的均衡点。 图7 政府和煤炭企业在补偿政策下的演化过程Fig.7 Evolution process of government and coal enterprise under subsidy policy 1) 政府实施静态奖惩措施无法有力推动煤炭企业开展智慧矿山建设,两者之间的演化路径呈现周期性的循环波动,此情况反映了当下政府和煤炭企业两群体博弈过程的长久性和周期性。因此,当地政府需要针对煤炭企业智慧矿山建设行为策略积极调整监管奖惩措施,为提高煤炭企业智慧矿山建设率采取最佳奖惩手段。 2) 政府实施动态奖励或惩罚措施可以有效抑制政府和煤炭企业博弈过程的波动性,系统仿真显示演化轨迹螺旋地内趋于稳定焦点,说明相应措施下存在演化稳定均衡点。因此,当地政府通过事先了解煤炭企业智慧矿山建设概率来调整自身的监管策略,并制定动态奖励或惩罚措施,合理确定奖惩力度,煤炭企业的智慧矿山建设策略会朝着积极且稳定的方向发展。 3) 政府在动态奖励或惩罚措施下提高惩罚力度对降低自身监管概率和提高煤炭企业智慧矿山建设率具有显著正向影响。因此,当地政府可以通过定期监管与提高煤炭企业维持现状或建设不达标等问题的罚款,降低自身监管率的同时提升煤矿企业群体的智慧矿山建设率。 4) 政府在动态奖励或惩罚措施下降低监管成本能有效提高政府监管率和煤炭企业智慧矿山建设率。因此,当地政府通过完善监管手段如建立智慧矿山系统平台实现远程监管,或多部门联动开展协同监管等,在降低政府监管成本提升监管效率的同时也能有效提高煤炭企业智慧矿山建设积极性。 5) 政府在动态奖励或惩罚措施下降低煤炭企业智慧矿山建设成本、提高智慧矿山建设效益或者减少企业维持现状的生产收益,能有效降低政府监管率,从而降低监管成本。 因此,当地政府可以通过人才引进、技术扶持以及开展专题培训等手段降低煤炭企业的智慧矿山建设门槛,同时也可采取智慧矿山生产税收减免、矿产资源优先配置以及推动建立智慧矿山联盟等手段提高企业智慧矿山建设的预期收益,从而以支撑手段代替监管手段推动煤矿企业智慧矿山建设,实现煤炭企业生产转型升级。




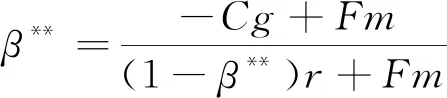


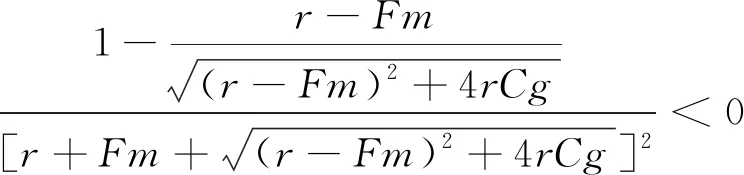
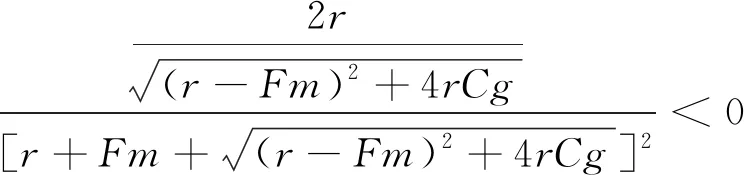
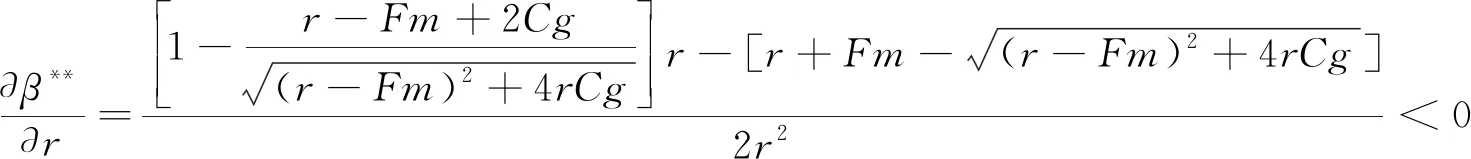
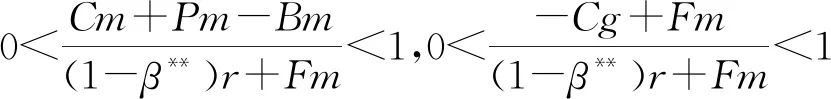
5 结 论

