基于云模型的基坑支护结构水平变形预测

陈明洋

（中铁建设集团有限公司 北京 100040）

1 引言

由于基坑开挖会破坏土体初始的地应力平衡状态，该过程的变形与工程所处地域的地质环境、开挖深度、开挖时间、土体结构、降雨、地下水渗流等众多因素有关，故开挖导致的基坑支护结构变形是个复杂、动态的变化过程，其中充满了不确定性，很难对其进行准确的预测，从而保证施工安全。

为了对基坑开挖过程中支护结构的变形进行准确预测，学者们运用了理论、数值模拟、数学统计等多种方法［1－4］。何伟等［5］基于灰色系统理论建立了预测基坑变形的GM（1，1）模型，并对隧洞施工过程中的变形进行了预测。李彦杰等［6］对BP神经网络进行了优化，建立了基于遗传算法-BP神经网络的深基坑变形预测模型，对宁波地铁某车站深基坑地下连续墙支护结构水平位移进行了预测。万荣辉等［7］将粗集理论算法和脊波神经网络算法结合在一起，建立了深基坑变形的预测模型，并成功应用于西南地区某市火车站南广场的基坑开挖预测。以上对基坑变形预测的理论方法均取得了一定的成果，由于基坑变形是个很复杂的非线性动力学现象，需要多重方法结合起来进行互补才能达到准确预测基坑变形的目的，引入新的智能方法开展基坑变形预测的研究仍然十分必要。

本文以不确定性人工智能［8］的理论为基础，将云理论应用到基坑变形的预测中。采用熵权法［9］来确定各指标的权重，建立了基坑支护结构变形预测的云模型，借助国内相关文献的实例检验了模型的可行性和准确性，为基坑支护结构变形预测问题的研究提供了一条新思路。

云模型对水泥土重力式支护结构水平变形进行预测，得到的预测值为在某个范围内的一系列离散点的集合。在实际工程中，预测人员可结合相关经验确定合适的预测结果，或者直接采用这些离散点集合的期望值作为预测结果。

2 云模型理论

云模型是李德毅院士［10］在随机数学和模糊数学的基础上提出的关于不确定性知识定性与定量直接相互转换的模型，现已成功运用到年降雨量的预测［11］、水质评价［12］、围岩等级评价［13］等多个领域。

2.1 云的定义

云模型可以在定性概念与定量表达之间相互转换，并且能反映出定性概念的不确定性，只用3个数字特征即可描述云模型：期望Ex、熵En、超熵He。相关定义如下：

设U是一个用精确数值表示的普通集合，称其为定量论域，C是U上的一个定性概念。对于U上的任意一个元素x，都存在一个具有稳定倾向的随机数μ（x），称作x对C的确定度，且x服从以Ex为期望，En′为标准差的正态分布，其中En′又是服从以En为期望、He为标准差的正态分布，则x对C的确定度满足：

2.2 云的数字特征

云模型用期望Ex、熵En、超熵He三个数字特征来整体表征一个概念。期望Ex是定性概念中最典型的样本，也是最具代表性的点；熵En用来描述定性概念离散程度的大小，反映了论域空间中可被概念接受的云滴的取值范围；超熵He表示熵En的熵，即表示熵的离散性大小，由熵的随机性和模糊性共同决定。

2.3 逆向云发生器算法

云模型数字特征的确定方法主要有指标近似法和逆向云发生器算法［14］，在支护结构变形量这方面目前还没有建立相关的评价指标体系，依据经验公式的指标近似法暂时不可行，所以本文选用基于统计数据来反算云模型数字特征的逆向云发生器算法，此方法不受到人为干扰，得到的数字特征更加客观准确。将收集到的案例数据作为p个云滴xq（1≤q≤p）进行输入，逆向运算输出得到云模型的三个数字特征（Ex、En、He）。

步骤如下：

（1）通过云滴xq计算样本均值：

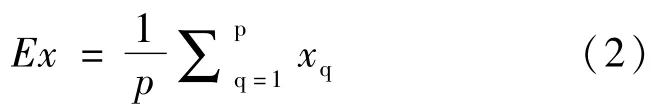
（2）计算样本方差：

（3）计算云滴的熵En和超熵He：

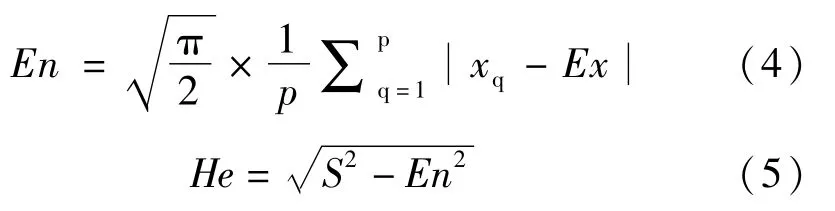
3 基于云模型的基坑支护结构水平变形预测

3.1 连续数据离散化

因为云模型的映射关系是基于定性概念的，所以在建立预测模型之前要将支护结构水平变形数据离散化［15］，转换为定性的概念。在数据分析中一般常用的连续数据离散化方法有等频率区间法和等距离区间法，但这两种方法没有考虑边界的模糊性，并且过于主观。本文考虑基于云模型的概念划分［16］，主要依据以下2个原理：（1）论域内的每个元素对定性概念的映射关系是一个统计属性，具有不确定性；（2）元素出现的频率越高则其对定性概念的贡献越大。结合模糊聚类方法［17］将支护结构的变形数据划分为若干个不同的定性概念，以达到连续数据离散化的效果。

3.2 基于熵权的指标权重确定

权重是表明影响支护结构水平变形的各个因素（即评价指标）重要性的权数，表示各个因素在总体评价中的作用，为了更加客观地确定各个影响因素的权重，减少人为主观的影响，采用熵权法［18］来确定各个评价指标的权重，算法步骤如下：

（1）设有m个评价对象，每个评价对象有n个评价指标，第i个对象的第j个指标记为xij，可以由得到评价对象和评价指标构成的原始数据矩阵X＝ （xij）m×n。

（2）根据评价指标对基坑变形影响效应的不同，对矩阵X用以下算法进行归一化处理，其中max（xj）和min（xj）分别表示第j个指标的最大值和最小值。

对越大越优的指标有：

对越小越优的指标有：

（3）求各指标的信息熵：

（4）计算各个指标的权重：

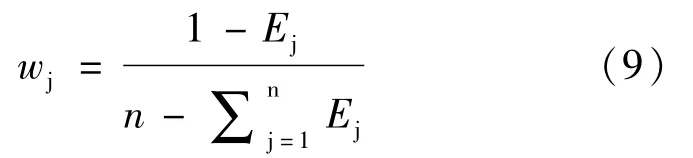
式中，wj为第j个评价指标的权重。

3.3 支护结构水平变形量的判定

根据某影响因素的实测值，结合各影响因素的权重，通过下式计算得到隶属于支护结构不同水平变形量的综合确定度，按照最大确定度原则来判断支护结构的水平变形量：

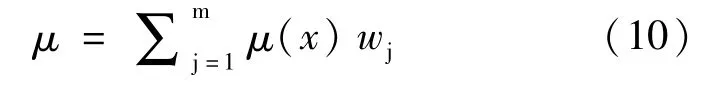
4 云模型的生成与检验

4.1 数据准备

影响水泥土重力式支护结构水平变形的主要因素有时间（从基坑开挖到开始计算位移的时间）、基坑挖深度、支护结构埋入基坑底部以下的深度、支护结构宽度、计算点深度。采用与文献［19］相同的40组样本，以其中35个用来建立预测模型，另外5个样本用来验证。在建模之前需先将各个因素的值进行归一化处理，处理后的第二、第三、第四因素为不变的常量，故在本例中不予考虑。因此考虑的主要影响因素有时间x1和计算点深度x2。数据归一化处理如下：对时间x1和计算点x2分别采用100 d和20 m为基数进行归一化处理，处理后时间和计算点深度无单位，水平变形量不进行处理，为原始数据，以mm为单位，具体数据见表1。

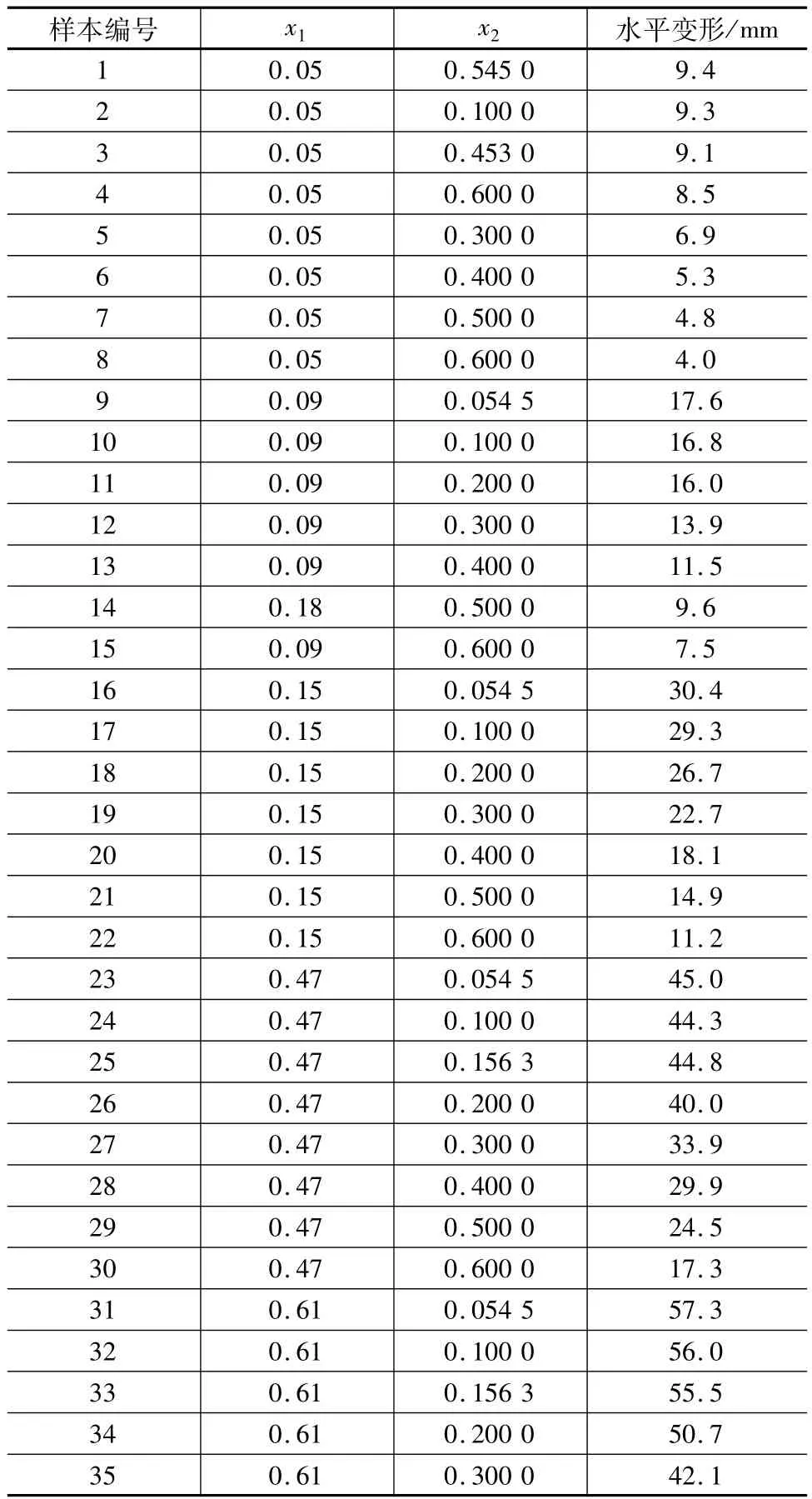
表1 实例样本

将支护结构水平变形量从小到大排列，使用模糊聚类方法将数据分为7组，即7个定性概念，分别为变形很小、小、较小、中等、较大、大、很大，对应的期望值取均值分别为 5.7、9.2、13.5、18.5、28.2、41.0、52.9，单位为 mm。利用离散化后的数据，依据逆向云发生器算法，得到不同水平变形量云模型的数字特征，见表2。

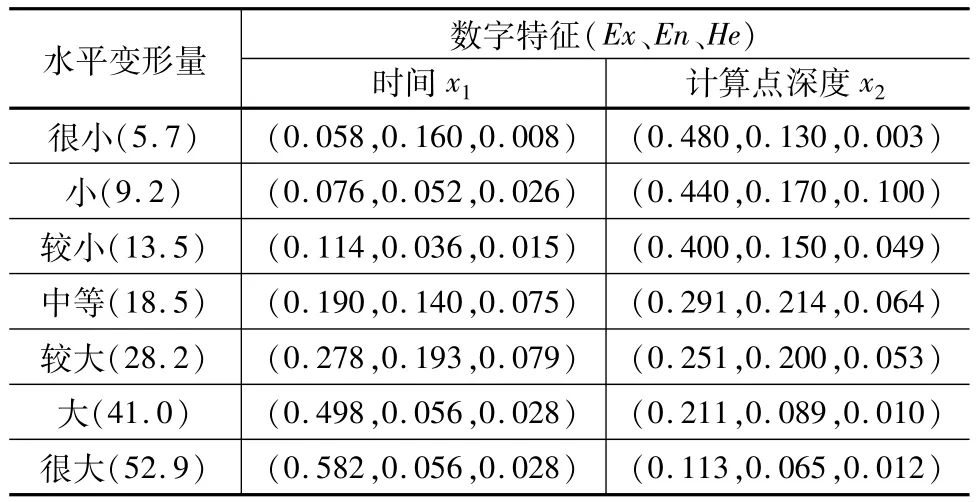
表2 不同水平变形量云模型的数字特征

4.2 模型生成

基于正态云模型理论和表2中的数字特征，对时间生成云模型，由7个散点图组成，如图1所示。对计算点深度生成云模型，如图2所示。

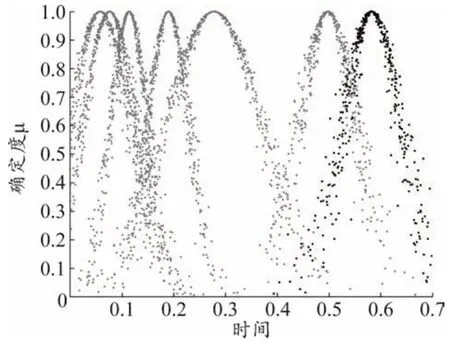
图1 时间云模型

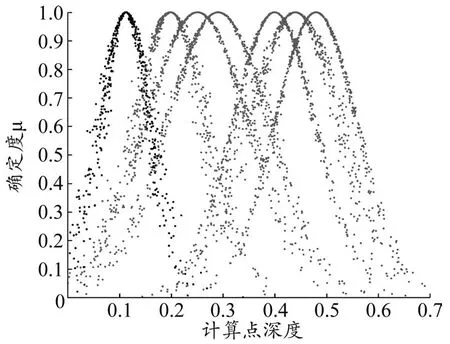
图2 计算点深度云模型

图1中，从左至右分别代表支护结构水平变形量很小、小、较小、中等、较大、大、很大对应的云。在图2中则刚好相反，从左至右分别代表支护结构水平变形量很大、大、较大、中等、较小、小、很小对应的云。

4.3 模型检验

依据表1中的35个样本，按照熵权法求权重的基本步骤来计算时间和计算点深度分别占的权重。其中在归一化数据时，时间越久，变形量越大，属于越大越好型，按照式（6）计算，计算点深度与之相反，属于越小越好型，采用式（7）计算。计算得时间和计算点深度的熵值和熵权见表3，结果表明，时间对支护结构变形的影响更大一些。

表3 各评价指标的熵权

对上述实例进行验证，根据公式（1）、（10）计算支护结构水平变形量隶属于不同变形量概念的确定度，依据最大确定度原则判断水平变形量。值得注意的是，云模型是一种不确定性的推理，每次计算结果都不同，但是都在某个范围内，是离散点的集合。因此计算100次，取其期望值作为预测结果，并计算误差，数据列于表4。由表4可以看出，预测值与实际值最大误差为8.7%，基本满足工程需要。

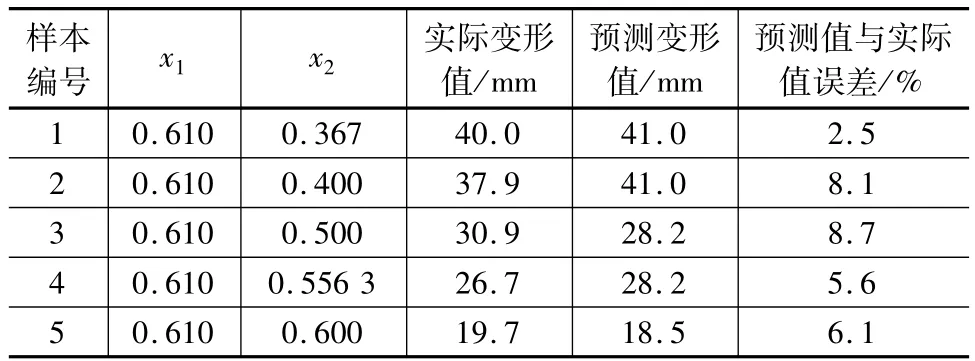
表4 预测结果与实际值比较

5 结论

本文的成功尝试不仅拓宽了云模型的应用范围，也为解决水泥土重力式支护结构水平变形预测中的不确定性问题找到新的方法，具有一定的实际应用价值。

云模型理论用于基坑支护结构水平变形预测还只是一个初步尝试，仍存在一些问题需要进一步研究，比如主要影响因素考虑不完全，用于统计的实例样本还可以进一步充实，使得建立的云模型更加完善，更加契合实际，预测结果更加准确。