一种辅助新型冠状病毒肺炎检测的肺实质分割算法

苏 赋，但 涛，方 东

（西南石油大学电气信息学院，成都610599）

0 概述

截至2020年12月31日，全球累计确诊82 981 032例新型冠状病毒肺炎病例，累计死亡1 809 633 例。新型冠状病毒对人类健康构成严重威胁。尽早发现新型冠状病毒感染的肺炎病例将有效阻断病毒传播。X 光胸片成像是检测新型冠状病毒的有效手段之一，然而由于人体胸腔结构复杂，除肺实质以外还包含了肋骨、脊椎、支气管等干扰部位，这将严重影响计算机辅助系统诊断新型冠状病毒肺炎患者，因此从X 光胸片中提取肺实质成为新型冠状病毒肺炎诊断任务中的关键环节。

图像分割技术是计算机视觉领域的重要研究方向，将图像分成若干互不交叉且分别具有相似性质的区域。传统图像分割技术主要依靠数字图像处理领域的分割算法，这些分割算法需要人为设定超参数，分割效果受人为因素影响较大。文献［1］结合Freeman 链码法和Bezier 曲线对传统图像分割技术进行改进，虽然在一定程度上提升了分割精度，但是仍需要人为设定超参数。

目前，国内外研究人员提出了大量基于深度学习技术的医学图像分割方法［2］并取得了实质性进展，其中最具代表性的是RONNEBERGER 等［3］提出的U-Net。该网络利用级联操作将编码器与解码器特征及图像高层信息与浅层信息进行有效融合，防止了卷积网络高层语义信息的丢失，能够充分表达上下文信息。文献［4］提出的V-Net 在网络结构上与U-Net 较接近，该网络主要应用于三维图像的特征提取，其中加入了残差连接架构，可有效缓解网络深度加深导致的梯度消失问题。文献［5］在U-Net 的基础上加入了残差连接模块有效解决了深层网络参数迭代迟缓甚至无法迭代的问题。文献［6］在全卷积网络结构中引入了空间注意力模块和通道注意力模块。文献［7］提出一种渐进式微调策略，将其应用于深度迁移学习网络以辅助诊断肺结节良恶性。文献［8］将表面波变换与脉冲耦合神经网络结合进行肺实质分割，有效抑制了肺部图像的干扰信息。文献［9］提出一种基于编解码模式的肺实质分割算法，该算法运用空洞空间金字塔池化［10］及多尺度图像输入充分提取图像特征。这些算法从更加高效的整合特征入手，提升了网络模型的特征提取能力，但是由于未考虑分割目标的形变会在一定程度上影响分割准确率等指标，且采用传统分割损失函数训练网络，因此无法有效提升网络对不同数据集的泛化能力。

本文在U-Net 的基础上提出一种结合编解码模式的肺实质分割模型。构建A 形特征融合模块（ABlock），充分学习深层特征的语义信息，避免了特征提取过程中的信息丢失。在深层卷积网络中，加入密集空洞卷积（Dense Atrous Convolution，DAC）模块［11］和残差多核池化（Residual Multi-kernel Pooling，RMP）模块［11］，扩大卷积感受野并提取上下文特征信息，同时改进可变形卷积（Deformable Convolution，DC）［12］和分割损失函数，使网络能自适应检测目标的各种形变，充分发挥卷积神经网络的特征提取能力。

1 相关理论

1.1 改进的可变形卷积

如图1所示，传统卷积使用规则的方块卷积核进行卷积运算。如图2所示，可变形卷积使用不规则的卷积核进行卷积运算。可变形卷积使网络进行卷积运算时重点关注感兴趣的局部区域，而不是统一使用方块卷积核扫描整张图像区域。

图1 传统卷积Fig.1 Traditional convolution

图2 可变形卷积Fig.2 Deformable convolution

传统卷积的操作步骤主要为：1）使用规则卷积核在输入特征图上进行特征采样；2）利用权重系数W对采样值进行加权求和。

对输入特征图x进行卷积采样可以得到输出特征图上的任意位点a0的特征值y（a0）：

其中：an为卷积核k上的所有位点。

在可变形卷积中，偏移量Δan（n=1，2，…，N，N=|k|）会间接改变规则卷积核的形状，因此改进的特征值y（a0）为：

可变形卷积实现流程如图3所示。设输入特征图大小为b×w×h×c，文献［12］单独使用一个神经网络预测位置偏移量Δan，输出特征图大小为b×w×h×2c。本文提出一种新的偏移量计算方法可使计算量减少1/2。改进的可变形卷积实现流程如图4所示。

图3 可变形卷积实现流程Fig.3 Implementation flow of deformable convolution

图4 改进的可变形卷积实现流程Fig.4 Implementation flow of improved deformable convolution

（w×h）大小的特征图X经过卷积核为k的规则卷积后得到S（i，j），如式（3）所示。将S（i，j）输入到sigmoid 函数σ得到Y（i，j），如式（4）所示。将Y（i，j）乘以（w×h）得到位置偏移量Aw×h×c，如式（5）所示。将原特征图位置编号矩阵G进行拉伸操作（Flatten）得到矩阵T，G中的每个通道号为0 到（w×h）的一维编号，如式（6）所示。位置偏移矩阵Z等于A加T，并限制Z的值在0 到（w×h）之间，如式（7）所示。

利用位置偏移矩阵Z提取原特征图中的像素值，将其进行拉伸操作后的原特征图记为X′、X′中的像素编号按矩阵T进行编号，将X′中编号对应的像素值如图5所示提取当前偏移位置及其上下左右共5 个像素值并求平均值，得到位置变换后的特征图Xoffset，并对Xoffset特征图进行卷积核大小为3×3 的卷积操作。

图5 位置变换后的特征图Fig.5 Feature figure after position transformation

1.2 空洞卷积

空洞卷积可以有效避免底层网络纹理细节信息的丢失，同时不增加网络的计算量。空洞卷积在传统卷积的基础上加入了膨胀系数。图6 给出了加入了膨胀系数为2 的空洞卷积。对于膨胀系数为r，卷积核尺寸为k的空洞卷积的感受野g计算如式（8）所示：

图6 空洞卷积Fig.6 Atrous convolution

2 肺实质分割算法

2.1 算法流程

图7 给出了本文算法流程，首先将输入图像经过直方图均衡化、翻转、拉伸等预处理操作，把处理好的图像分批次输入分割模型中得到预测值（即1 张像素值为0 到1 的图像），用预测值与标签二值图像计算损失函数进行网络参数优化。

图7 肺实质分割算法流程Fig.7 Procedure of pulmonary parenchyma segmentation algorithm

2.2 网络结构

本文采用基于编解码模式［13］的U 形神经网络（AD-U-Net）。AD-U-Net 分为编码部分、深层特征融合部分和解码部分，并使用级联操作将编解码特征图进行融合，避免高层特征纹理细节信息丢失。AD-U-Net 结构如图8所示。

图8 AD-U-Net 结构Fig.8 AD-U-Net structure

2.2.1 编码部分

由于神经网络中浅层特征纹理细节信息丰富，高层特征语义信息丰富，在图像分割中决定分割质量的因素通常存在于纹理细节中。本文使用4 个最大池化层得到4 个不同尺度的特征图，并利用级联操作向4 个尺度特征图输入不同尺度的输入图像以避免深层网络纹理细节信息的丢失。编码部分每层采用2 组3×3 卷积操作（3×3 conv）加上批归一化（BN）和Relu 激活函数，并使用最大池化（Maxpooling）进行下采样。在每层卷积后所得的特征图不仅要传入最大池化层进行下采样，而且要运用级联操作输入到深层特征融合部分和解码部分进行特征融合，从而充分表达每层所提取的不同特征。

2.2.2 深层特征融合部分

由编码部分输入的图像如果不采用特征融合操作，直接将编码部分最后一层输出与解码部分相连，则编码部分提取的丰富特征信息在网络参数传递过程中有极大概率会丢失，最终影响分割质量。本文提出一种A-Block 结构，如图9所示，黑色特征层为编码器各层的输出特征图，白色特征层为编码器最后一层的特征图。

图9 A-Block 结构Fig.9 Structure of A-Block

将编码器最后一层的特征图经过1 次3×3 卷积和3 次3×3 转置卷积（3×3 upconv）上采样，得到4 个特征图。将上采样得到的特征图与对应尺度的黑色特征层进行相加操作（Add）和拼接操作（Concatenation），将特征图叠加融合，最终得到输出特征图（output）。

除此之外，深度特征融合部分还加入了密集空洞卷积模块［14］和残差多核池化模块［15］。如图10所示，将特征图用不同膨胀系数（r）的空洞卷积进行特征提取，得到不同感受野的特征图，在DAC 中首先进行一次膨胀系数为1 的3×3 卷积后，并列进行多次不同膨胀系数的卷积操作，卷积通道数（C）均设置为512。值得注意的是不同膨胀系数的膨胀卷积可有效提取多尺度信息，最后将这些并列的卷积操作进行拼接操作后输出得到多尺度特征映射。本文将A-Block 中A 点处的输出特征图进行一次kernel size为1、stride 为2 的反卷积，改变特征图大小并调整通道数，经过sigmoid 激活函数得到深层网络预测特征图，将该预测特征图与标签二值图像进行对比并计算损失函数。本文通过深度监督（Depth Supervision，DS）机制［16］指导深层网络的参数优化，避免由于网络深度增加导致的优化梯度消失问题。

图10 密集空洞卷积模块结构Fig.10 Structure of DAC module

在医学图像中，分割目标大小及形状因为不同症状的影响变化较大。文献［11］使用一种残差多核池化模块来解决该问题，其结构如图11所示。该模块主要依靠多个不同尺度的最大池化来检测不同大小的对象。残差多核池化模块首先采用4 个不同大小的池化核对全局上下文信息进行编码，然后将池化后的多尺度特征图进行拼接操作，最后引入一个1×1 卷积及批归一化进行特征降维。

图11 残差多核池化模块结构Fig.11 Structure of RMP module

2.2.3 解码部分

当神经网络输入信息量很大时，模型参数也非常庞大，以至于神经网络无法重点关注起决定性作用的部分参数。在解码部分，本文采用可变形卷积，在每层解码模块的开始加入一个改进的可变形卷积模块，将解码模块、编码模块、深层融合模块的输出特征图进行拼接操作后输入可变形卷积模块中。该模块将自适应地对图像中感兴趣的区域进行特征提取，变相地改变了卷积形状，并在卷积过程中不断地识别图形中的感兴趣区域。普通注意力模块是在进行规则卷积后对得到的特征图进行筛选操作。该方法比较依赖人为设定不同尺寸的卷积核对多尺度目标的检测，而可变形卷积无需人为设定不同尺寸的卷积核，即可实现对多尺度目标的检测。每层解码模块引入了可变形卷积和3×3 普通卷积，并用转置卷积进行上采样，实现特征图的尺度变换。

2.3 损失函数

本文引入类距惩罚项改进分割损失函数，目的是增大类间距并缩短类内距。Tversky 损失函数的定义如式（9）所示：

其中：pi表示像素i属于肺实质的预测概率；表示像素i属于背景的预测概率；yi表示像素i属于肺实质的真实标签值；表示像素i属于背景的真实标签值；ε是一个极小的数，避免分母为0；α和β分别用于控制假阳性和假阴性的权重。本文在Tversky 损失函数的基础上进行了改进，加入了类距惩罚项，定义如式（10）所示：

其中：a表示预测为肺实质，标签为肺实质的所有像素的平均值；b为预测为背景，标签为背景的所有像素的平均值；d表示标签为肺实质的预测值的所有像素的平均值；e表示标签为背景的预测值的所有像素的平均值。在式（10）中，多项式第2 项和第3 项即为控制类内距（Sn）和类间距函数（Sp）。如果仅将类内距和类间距加入到损失函数中以寻求减少（Sn-Sp），那么该法将缺乏优化灵活性。

由于该对称优化方法对类间距和类内距的惩罚力度是严格相等的，因此在进行优化时Sn和Sp具有相同的梯度。如图12所示，Sn已非常小，如果按照对称的类距损失函数进行参数优化，那么Sn将继续以较大的梯度减小，从而到达决策边界T所在的位置。该方法效率低，且收敛状态模糊。由图12 可以看出，点T和T′均位于决策边界上，由于对称的类距损失函数允许模糊的收敛状态，因此收敛速度减慢，收敛状态多样化。

图12 传统类距损失函数的收敛情况Fig.12 Convergence of traditional class distance loss function

文献［17］为类距损失函数进行优化，将（Sn-Sp）修改为（λnSn-μpSp），允许Sn和Sp以不同的步调进行学习。如图13所示，在加入λn和μp后将使类间距和类内距的下降梯度和收敛状态相适应，决策边界呈圆弧形。对于Sn和Sp，加入了控制不同相似度函数收敛梯度的加权因子。将正负样本标签与预测值之间的欧式距离作为加权因子，当类内距过大时，权重参数将会附加给类内距相似度函数更高的权重，提高其在优化时的梯度。因此，相似度损失函数可以按照各自不同的步调进行参数优化，提升了函数优化的灵活性和决策边界的泛化能力。

图13 圆损失函数的收敛情况Fig.13 Convergence of circular loss function

3 实验与结果分析

3.1 实验数据与环境

实验采用5 000 张X 光胸片数据及其对应的肺实质人工分割二值图像。X 光胸片数据包含正常、已感染新型冠状病毒肺炎和患有其他疾病的胸部X光成像，其中每张图片分辨率均为512 像素×512 像素。将80%的图像作为训练集，20%的图像作为测试集。实验硬件环境为NVIDIA RTX 2080 Ti GPU，Intel Core i7 CPU，采用Adam 优化器，并且学习率设定为1e-4，batch size设定为8。

3.2 评价指标

本文评价指标包括准确度（Acc）、Dice 系数、敏感度（Sen）和Jaccard 指数，具体计算公式如式（11）～式（14）所示：

其中：TTP表示标签分割图像和预测分割图像的肺实质公共区域的像素数量；FFP表示在分割预测区域内而在标签分割区域外的像素数量；TTN表示标签分割图像和预测分割图像的非肺实质公共区域的像素数量；FFN表示在分割预测区域外而在标签分割区域内的像素数量。

3.3 结果分析

3.3.1 损失函数对分割结果的影响

经过统计得出，数据集中正负样本比例严重失衡，Tversky 损失函数对于FFN和FFP的检测权重是不相等的，可以根据数据的实际情况改变相应的权重值，从而减弱数据样本分布不平衡对分割结果造成的不良影响。测试并比较Tversky 损失函数（见式（9））和改进的Tversky 损失函数（见式（10））的性能，损失函数对分割结果的影响如表1所示。可以看出，在使用改进的Tversky 损失函数后，分割算法的各项性能指标均有不同程度的提升。

表1 损失函数性能对比Table 1 Performance comparison of loss function %

由于使用sigmoid 函数，预测值被限定在0.0 到1.0 之间，将预测结果分为10 个区段，分别统计预测值在各个区段中的像素数量，基于Tversky 损失函数和改进Tversky 损失函数的预测数据分布结果如图14 和图15所示。可以看出，在改进的Tversky 损失函数后像素预测值主要分布于0.1～0.3 和0.7～1.0，而0.3～0.7 的预测数相对损失函数不断减少，像素预测值大量分布在0.0 或者1.0 附近，表明改进的Tversky 损失函数的鲁棒性更强。对比图14 与图15可以看出，基于改进Tversky 损失函数的预测数据分布两极分化更加明显，符合预期效果。

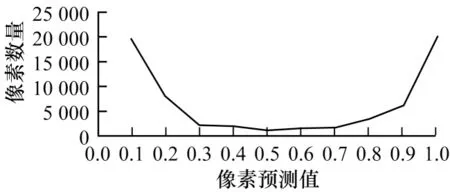
图14 基于Tversky 损失函数的预测数据分布Fig.14 Prediction data distribution based on Tversky loss function

图15 基于改进Tversky 损失函数的预测数据分布Fig.15 Prediction data distribution based on improved Tversky loss function

3.3.2 消融实验

由A-Block、DAC 模块、RMP 模块、DC 和DS 机制组成的5 种改进方案对分割性能的影响如表2所示。可以看出，A-Block 和DC 相较其他模块和机制对于分割结果的影响较大。A-Block 将上下文信息充分融合，避免特征提取过程中的信息丢失，从而提升分割精度。DC 作为一种特殊的注意力机制，使网络能自适应检测目标的各种形变，充分发挥了卷积神经网络的特征提取能力。DS 机制可以有效指导深层网络的参数优化，有效避免了随着神经网络深度加深导致的网络训练梯度消失和收敛速度过慢等问题。

表2 5 种改进方案对分割结果的影响Table 2 Influence of five improved schemes on segmentation results %

3.3.3 算法对比实验结果分析

将本文提出的AD-U-Net 与U-Net［3］、CE-Net［9］、U-Net++［18］、U2-Net［19］、U-Net 3+［20］等5 种目前表现较好的神经网络进行分割性能对比，结果如表3所示。可以看出，本文基于AD-U-Net 模型的分割算法的准确度、Dice 系数、敏感度和Jaccard 指数分别达到98.16%、98.32%、98.13%和98.54%，相较对比模型有不同程度的提升。因此，本文提出的基于AD-U-Net模型的图像分割算法能有效实现肺实质分割。

表3 基于6 种神经网络模型的图像分割算法性能对比Table 3 Performance comparison of image segmentation algorithms based on six neural network models %

4 结束语

本文提出基于编解码模式的肺实质分割算法，运用特征融合思想，在深度融合模块中采用A-Block、密集空洞卷积模块和残差多核池化模块充分融合上下文信息。通过带有可变形卷积的注意力机制对编解码特征进行融合，提升卷积神经网络对检测目标形变的适应能力。设计类距惩罚损失函数，使网络预测结果更加稳定。实验结果表明，该算法能实现肺实质部位的有效分割，相比其他算法分割性能更优。后续将探索并研究更加高效准确的分割算法，提升新型冠状病毒肺炎的检测准确率，并进一步扩展该分割算法在其他医学图像处理中的应用，提升其普适性与实用性。