柔性伞衣织物的自由变形折叠建模及其充气机制研究

张思宇， 余 莉， 贾 贺，2， 刘 鑫

(1. 南京航空航天大学 飞行器环境控制与生命保障工业和信息化部重点实验室， 江苏 南京 210016； 2. 北京空间机电研究所， 北京 100094)

冲压翼伞由柔性织物构成，是一种非展平曲面构成的多气室-双翼面结构降落伞。相较于传统平面圆形伞，冲压式翼伞的滑翔比高，操作性良好，在民用、军事等领域得到广泛应用[1-3]。在翼伞工作过程中，决定其成败的最主要因素是柔性伞衣织物的折叠展开充气过程，很多降落伞失效事故都与柔性伞衣的折叠展开有密切关系[4]。据不完全统计，翼伞的不完全开伞概率远高于常规圆形伞。翼伞由于伞衣织物的结构布局更加复杂，因此织物的折叠建模问题一直是研究的难点。

降落伞柔性伞衣织物的折叠充气展开过程时间较短，实验数据采集困难且离散性大，数值模拟的方式已经成为揭示伞衣展开充气过程工作机制的有效手段[5-7]。在数值计算时，柔性伞衣织物的折叠建模是首先需要解决的问题。降落伞伞衣属于柔性织物，而服饰是柔性织物的重要应用领域，目前服饰织物褶皱折叠仿真方法主要有基于几何方法建模[8-9]、基于物理方法建模[10-11]和基于综合方法建模[12-13]。但是，服饰折叠不涉及充气展开过程，因此不能直接应用于降落伞。柔性伞衣织物的折叠建模更为复杂，目前主要采用直接折叠建模法[14-16]、初始矩阵法[17-18]以及逆向力建模法[19-20]。前2种折叠建模方法的共同特征是必须建立初始折叠模型，折痕或褶皱处单元节点坐标须直接确定，因而只适用于相对简单的二维平面组成的织物进行折叠，如普通圆伞、汽车安全气囊和空间充气管等织物折叠。逆向力建模通过对展开织物施加合理的外载荷，基于柔性织物受力变形的原理实现折叠建模，但由于柔性壳单元的位移对载荷大小、加载时间和施加方式很敏感，且建模过程中不遵守物理守恒定律，只适用于简单的、具有展平面的织物建模，无法保证分析结果的准确性，实际上很难实施。

许多新型充气织物的形状和折叠方式都很复杂，很难用上述方法进行建模，如冲压翼伞上下翼面为柔性非展平曲面，内部为开孔肋片构成的多气室结构，结构的复杂性导致其无法采用现有常规折叠方法建立折叠模型。翼伞的折叠建模问题作为翼伞研究领域的难点，一直备受国内外学者关注。

针对这一难点，受到计算机三维动画特效制作的启发，借鉴了曲面造型的思想，基于翼伞柔性伞衣织物的真实折叠特点，本文提出基于直接约束型曲面变形技术的柔性伞衣织物折叠建模方法。该方法采用直接约束型曲面变形技术，通过操纵控制节点的移动获得折痕坐标，实现曲面变形，基于矩阵坐标变换进行展向压缩，解决了多气室冲压翼伞柔性伞衣织物的展向折叠建模问题，对进一步基于数值耦合方法开展翼伞充气机制的研究具有一定的参考意义。

1 研究对象与思路

采用多气室柔性冲压翼伞为研究对象[21]，翼伞弦长2.74 m，平铺展长5.48 m，伞绳长3.36 m，有7个气室，每个气室中间由一个非承载的开孔肋片分开，共有14个半气室。柔性伞衣和伞绳材质均为锦纶，二者的材料参数如表1所示。

表1 伞衣织物与伞绳材料参数Tab.1 Parameters of canopy fabrics and cord lines

本文的研究思路如图1所示。在柔性翼伞织物的折叠建模及其充气过程中，本文提出一种基于曲面自由变形技术(FFD)方法的柔性伞衣织物折叠建模方法获得展向压缩模型，基于任意拉格朗日-欧拉(ALE)方法开展流固耦合的充气展开过程仿真。

图1 研究思路Fig.1 General framework

2 柔性伞衣织物折叠建模方法

2.1 自由变形方法

1986年，Sederberg等[22]提出FFD方法，该方法仿照弹性物体受外力后发生相应的变形这一物理现象，将待变形的几何模型嵌入到控制晶格中，利用晶格节点移动，将晶格的变形传递给嵌入模型，达到对模型折叠的目的。本文借鉴了这种曲面造型的思想，将这一技术应用于翼伞折叠建模，提出了多气室冲压翼伞柔性伞衣织物的展向折叠建模方法。采用直接约束型曲面变形技术，通过控制节点移动实现曲面变形，变形后约束点或线的变形位置准确。

图2示出伞衣的待变形区域和控制点。右侧曲面表示待变形区域，左侧代表不变形区域，P为约束点，P*为移动变形后的约束点，待变形区域内的任意一点记作Q，由此得到△PP*Q所在平面与边界线l的交点Qc。在此基础上，得到一个由Qc、P*、P这3点组成的新三角形△PP*Qc。

图2 待变形区域和控制点Fig.2 Deformed area and control nodes

在△PP*Qc截面，如图3所示，点Q在直线QcP的投影点是Qp，从而得到参数

d=|Qp-P|/|Qc-P|

(1)

式中,Qp、Qc、P分别为Qp、Qc、P这3点的坐标向量。将d代入直线参数方程

Q*=dQc+(1-d)P*

(2)

由此得到点Q变形后的约束坐标向量Q*。若存在多个约束点Pn，则单独计算点Q在各个约束点Pn影响下的偏移量，即每个约束方程存在1个变形参数dn，则可以获得多组偏移量，最后对所有偏移量进行加权计算。对于常规变形，采用均权计算。

图3 控制点截面Fig.3 Section of control nodes

2.2 齐次坐标变换

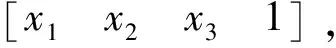
(3)

(4)

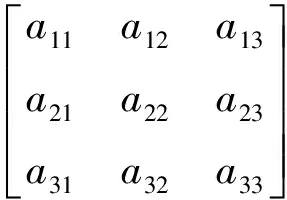
2.3 初始应力修正

在柔性织物的折叠建模仿真过程中，很难保证折叠模型褶皱处的充气展开状态与实际工程情况相同，这种误差会影响到数值计算的准确性。本文引入初始应力修正几何误差，使几何折叠模型具有初始本构力学特征，如图4所示，图中Li(i=1,2,3)为Lagrange坐标。由于折叠前后的几何拓扑结构不变，因此可得到从映射构型Lmap到参考构型Lref的每个单元的应变量：

ε=B(Lref-Lmap)

(5)

式中:B为几何函数矩阵；参考构型Lref表示没有初始误差的网格坐标;映射构型Lmap表示带有初始误差的折叠后网格坐标。

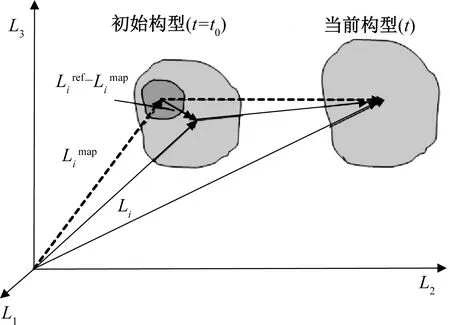
图4 初始应力修正原理Fig.4 Principle of initial stress modification

根据材料本构方程获得修正应力

σ=Dε

(6)

式中,D为弹性系数矩阵。

初始应力修正方法的具体提出及其在降落伞伞衣处理的比较验证，在文献[15]中有详细的阐述，本文不再赘述。

3 柔性伞衣织物充气展开控制方程

3.1 流固耦合控制方程

翼伞折叠模型的充气过程采用任意拉格朗日-欧拉(ALE)方法[24-25]进行数值模拟，流场控制方程为

(7)

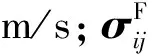
式中：p为压强，Pa;δij为Kroneckerδ函数，μ为动力黏度，N·s/m2。

翼伞结构和流场之间耦合，采用Lagrange方程进行数值计算：

(8)

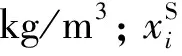
ALE网格的运动控制方程为

(9)

式中,Li为Lagrange坐标，m。

对上述控制方程采用中心差分方法进行全耦合计算。对每个节点，更新流场和结构的位移x和速度u：

(10)

式中:M为质量对角矩阵;Fint和Fext分别为内力矢量和外力矢量。

3.2 材料模型

对伞绳采用一维线弹性本构方程模拟其材料性能，即

σx=Eεx

(11)

式中：ε为应变；E为弹性模量，Pa。伞衣采用Kirchhoff材料进行模拟，其主要特点是小应变、大转动，从而得到

σ=J-1ESET

(12)

其中:J为雅可比矩阵;E为Green应变;S为第二类Piola-Kirchhoff应力,公式为

Sij=CijklEkl

(13)

式中：Cijkl为四阶切线模量张量，Pa；Ekl为Green应变。由于本文翼伞伞衣采用各向同性的线弹性材料，同时采用3节点壳单元进行计算模拟，属于平面应力问题，所以有

(14)

式中，υ为泊松比。

4 柔性伞衣织物折叠及充气过程

4.1 折叠建模

翼伞的真实展向折叠状态如图5所示。基于其真实的物理折叠特点，采用本文方法构建柔性翼伞的数值折叠模型。为保证折叠建模过程的高效性,只对参与折叠的上下翼面和肋片进行变换操作，得到翼伞伞衣的展向折叠模型。

图5 伞衣织物的真实折叠图Fig.5 Actual folded canopy fabrics

首先，建立伞衣织物的初始几何模型。基于三维建模软件建立伞衣充满状态下的几何外形，根据折叠要求在上下翼面各气室中间建立折痕线，并用三角形网格划分柔性伞衣的几何模型，如图6所示。然后，根据折叠的要求，建立约束控制及其对应的约束关系，如图7所示。其中点1、2、3、4为变形控制点，点5、6、7、8为固定约束点。

图6 伞衣初始几何模型Fig.6 Initial geometric model of canopy

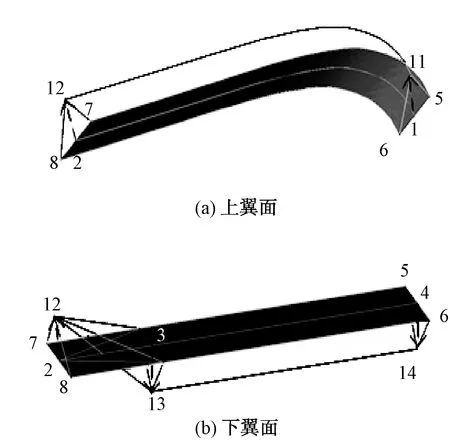
图7 上下翼面的控制节点及约束Fig.7 Control nodes and constraints of upper (a) and lower (b) wings surface

接下来进行上下翼面变形。将翼面单元设置为变形域，将图7中控制点1、2、3、4分别投影至变形后的位置点11、12、13、14处(根据物理真实折叠确定)，弧线1-2和折线2-3-4上的各个点的投影的最终位置无法确定，根据自由变形方法得到翼面变形结果,如图8所示。半气室的最终变形结果如图9所示，开孔部分为翼肋，由于开孔，因此图中开孔处显示的网格为孔后气室外侧伞衣的网格。

图8 上下翼面投影变形Fig.8 Projection distortion of upper (a) and lower (b) wings surface

图9 变形后的气室Fig.9 Deformed cells

采用上述操作，获得柔性伞衣织物整体的变形模型。最后采用齐次坐标变换方法，对伞衣各气室进行展向压缩，由于本文不涉及投影与缩放变换，因此a14,a24,a34,a44均为0。最终的翼伞折叠模型如图10所示。

图10 伞衣织物展向压缩Fig.10 Spanwise folded canopy fabrics

4.2 充气过程

为验证本文翼伞柔性伞衣织物折叠建模方法的准确性，采用空投实验进行对比验证。冲压翼伞以0攻角充气。对柔性伞衣织物结构周围的绕流流场网格进行加密处理。本文折叠建模方法仿真计算得到的开伞动载结果与空投实验数据对比如图11所示。

图11 开伞载荷变化Fig.11 Variation of opening load

从图11可以看出，数值计算结果和空投实验结果的变化趋势规律相似，仿真得到的开伞载荷峰值出现时刻略早，这和伞衣的包装方式有关。仿真的载荷峰值大小为4 760 N，和空投实验结果4 963 N相比，误差为4%，因此，本文的伞衣织物建模方法与充气计算误差满足柔性伞衣织物开伞仿真计算要求。计算得到的翼伞柔性伞衣织物外形结构及流场变化如图12所示。

从图12可以看出，在柔性伞衣织物的初始折叠状态时，织物之间由于存在一定的压缩率，因此结构间空隙较小，伞衣周围流场与载荷体相似，产生对称绕流现象，说明本文的翼伞折叠建模方法压缩率高，可完全满足实际建模要求。此后，随伞载系统运动，柔性伞衣的各气室逐渐充气形成充满翼型，而且各细节处伞衣均可正常充气展开，说明本文方法通过初始应力修正使得几何折叠模型具有了初始本构力学特征，降低了柔性伞衣织物充气展开时的应力集中和网格畸变现象，提高了数值计算的准确性，降低了折痕褶皱对计算稳定性的影响。

图12 充气过程结构及流场变化Fig.12 Evolution of structure and flow field during inflation. (a) Velocity vector contour; (b) Pressure contour

综上认为，本文基于曲面自由变形建立的多气室双翼面冲压翼伞伞衣织物折叠建模方法可以实现大体积压缩比的柔性伞衣织物折叠建模，解决了冲压翼伞柔性伞衣织物无法采用现有折叠方法建模的难题，从而使得翼伞充气研究不仅仅限于实验与动力学方法，基于数值耦合方法开展柔性翼伞充气机理研究成为了可能。

5 结 论

本文以多气室柔性冲压翼伞为研究对象，考虑其伞衣织物结构的复杂性，基于物理真实折叠特点，提出了基于自由变形的新型柔性伞衣织物折叠建模方法，通过充气过程流固耦合数值计算与空投实验的对比验证，得到以下结论。

1) 本文的折叠建模方法高度还原了柔性织物的物理真实折叠状态，同时通过坐标矩阵变换达到了较高的压缩率，实现了大体积压缩比的翼伞折叠建模要求。

2) 本文的折叠建模方法解决了非展平曲面无法采用现有模型折叠压缩的问题，同时采用初始应力方法修正几何误差，使几何折叠模型具有初始本构力学特征，减少了展开时的应力集中和网格畸变现象，提高了数值计算的准确性。

3) 本文折叠方法使得翼伞充气研究不仅仅限于实验与动力学方法，基于数值耦合的翼伞充气机制研究成为可能。同时也可应用于其他复杂充气式柔性织物的折叠建模研究，对充气式再入器、可展开式空间站等新型柔性织物装置的折叠方式设计和优化提供了参考。