基于有限区间云模型的地面塌陷危险性评价

刘懿俊，谭 飞，焦玉勇，汪 君，王伟垣

(1.深圳市地质局，广东 深圳 518023;2.中国地质大学(武汉)工程学院，湖北 武汉 430074)

随着经济的不断发展和城市化进程的不断加快，与人类活动关系密切的城市地面塌陷现象发生的频率也越来越高。因此，对城市各区域开展地面塌陷危险性评价就显得尤为重要。地面塌陷的危险性评价是一个综合性问题，涉及工程地质条件、天气、人类工程活动等因素，既有确定性指标，又有非确定性指标，其影响因素多、评价难度大。近年来，国内外在该领域做了大量的研究工作，提出了各种各样的地面塌陷危险性评价方法。如韩亚等从地质环境条件、采矿工程活动两个主要因素着手，采用模糊综合评价方法对河南城郊煤矿地面塌陷危险性进行了综合评价，确定了隶属函数，构建了模糊评价矩阵，并利用层次分析法确定了各影响因子的权重，进而建立了矿区地面塌陷危险性评价模型；Li等考虑岩溶发育、覆盖层条件和水文地质条件等因素，采用BP神经网络建立了武汉市岩溶地面塌陷危险性评价模型，并进行了分区评价。上述这些理论和模型在很大程度上完善了地面塌陷危险性评价体系，但自身仍存在一些不足之处。例如：模糊综合评判法在评价过程中计算复杂，对指标权重矢量的确定主观性较强，易出现超模糊现象；神经网络算法计算复杂，获取的样本代表性不强，拟合速度难以控制。

地面塌陷危险性评价中各种影响因素是不确定的，不仅具有随机性，而且还具有模糊性，有限区间云模型是基于传统模糊集理论和概率论提出的一种有效的定性概念与其定量之间不确定性的转换模型，能够同时考虑一定区间内信息的模糊性和随机性，因此常被用来处理定性与定量信息的相互转换问题。如戴兴国等将有限区间云模型应用到边坡稳定性评价中，并通过实例验证了该方法是有效可行的；张润来等探讨了有限区间云模型，并利用该模型对巷道冒顶危险性进行了评价。由于这些研究取得了很好的结果，因此本文通过引入评价指标服从均匀分布和正态分布的有限区间云模型，采用改进的层次分析法计算指标的权重，使含有不确定性特点的指标值与分级变量之间产生映射，从而使得到的地面塌陷危险性评价结果更具有合理性。

1 有限区间云模型的理论基础

1.1 有限区间云模型

设

U

是一个精确数值表示的定量论域，

C

是

U

上的一个定性概念，若存在任意的定量元素

x

∈

U

，且

x

是定性概念

C

上的一次随机实现,

x

对

C

的确定度

μ

(

x

)=(0,1)是有稳定倾向的随机数，即：

μ

:

U

→[0,1],∀

x

∈

U

,

x

→

μ

(

x

)

(1)

则

x

在论域

U

上的分布称为云，每个点(

x

,

μ

(

x

))称为一个云滴，并用期望

E

、熵

E

、超熵

H

3个特征值来表征这一概念。

(2)

(3)

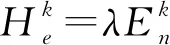
(4)

指标分类界限值同属于相邻2个等级，且两个级别间相互联系、互不干扰，由正态隶属函数可知，指标界限值同属于2个等级的确定度为0

.

5，其正态分布函数阶数的计算公式如下:

(5)

1. 2 正向有限区间云发生器

正向有限区间云发生器是实现定性概念转化为定量概念最主要的媒介，利用有限区间云模型特征参数

E

、

E

和

H

，结合指标等级特征和想要生成的云滴数

N

，可得到由

N

个云滴组成的定量值以及云滴图。当指标处于两端等级云均值之间的区间，此时

x

服从有限区间里的正态分布；当指标远离期望

E

，此时

x

服从确定度为1的均匀分布。综上所述，

x

服从有限区间里的均匀分布和正态分布公式如下：

(6)

2 地面塌陷危险性评价模型

2.1 改进层次分析法的算法及流程

在整个地面塌陷危险性评价过程中，云模型理论构成整个评价体系的主体，而指标权重的赋值是分类结果是否合理的关键。本文采用改进的层次分析法来确定指标的权重，以减小人为主观判断模糊性对评价结果的影响，避免重复性的计算工作。改进的层次分析法的算法及流程如下：

(1) 根据层次分析(AHP)法的基本原理，建立多因素层次结构模型。

(2) 比较每层因素对上一层某因素的贡献率，采用三标度法对因素进行两两比较，构造比较矩阵：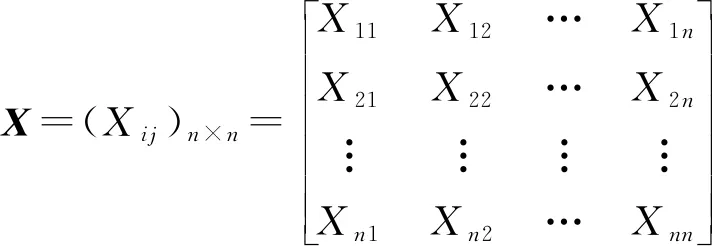

(7)

比较矩阵元素

X

表示因素

X

与因素

X

相比的重要性程度，其取值大小见表1。

表1 比较矩阵各元素的取值(三标度法)

(3) 按下式计算重要性排序指数

r

：

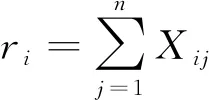
(8)

(9)

(10)

(11)

(7) 利用下式计算下层因素对上层因素的贡献率

ω

：

(12)

(8) 利用上述各层次间计算结果来计算指标的主观权重

ω

:

ω

=

ω

×

ω

(13)

式中：

ω

为指标层某因素对应准则层因素的贡献率;

ω

为相应准则层因素对目标层的贡献率。

2. 2 综合确定度的确定

基于公式(6)，可以计算出某指标实测值或评估值

x

隶属于某个等级云的隶属度；再结合各指标的权重，计算出样本指标的综合确定度

μ

:

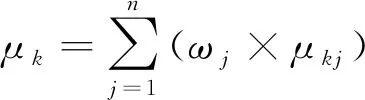
(14)

式中：

μ

为样本中第

j

个指标的实测值或评估值处于某一等级的确定度。参照综合确定度取值，按最大隶属度原则可得出最终的隶属等级

L

:

L

=max{

μ

,

μ

,…,

μ

}

(15)

2.3 地面塌陷危险性评价流

地面塌陷危险性评价的具体流程，见图1。

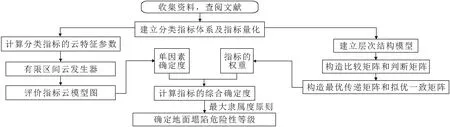
图1 地面塌陷危险性评价流程

3 案例应用研究

3.1 评价指标体系的建立与指标分级标准

影响地面塌陷危险性评价的因素错综复杂，其中最主要的因素为工程地质条件、天气、人类工程活动。迄今为止，其评价指标的选取在工程界和学术界都尚未达成统一的标准，现行的做法通常是经验选取法，依据不同的研究对象制定不同的评价标准。由于评价指标选择的合理性与否直接关系到最终结果的可靠性，因此在建立评价指标体系时应按照系统性、代表性、存异性、易获取、易量化等原则。通过综合分析研究区域内的工程地质条件,本文选取月降雨量、路基土回填程度、交通荷载等9个评价指标建立了地面塌陷危险性评价指标体系，各评价指标具体的分级标准见表2，运用正向有限区间云发生器分别生成各分类指标隶属于各级别的云滴图，见图2。

表2 地面塌陷危险性评价指标的分级标准表

图2 地面塌陷危险性评价分类指标隶属于各级别的云滴图

3.2 指标权重的确定

利用层次分析法建立地面塌陷危险性评价的层次结构模型，见图3。

图3 地面塌陷危险性评价层次结构模型

将准则层

B

、

B

、

B

进行两两综合比较构造比较矩阵，根据深圳市福田区地勘资料，参考实际地区工程实例，并结合专家意见，得到准则层中各要素的权重，见表3。

表3 比较矩阵及准则层权重

同理，可得到指标层各指标的权重，并结合准则层权重，最终得到指标的主观权重，见表4。

表4 比较矩阵及指标的主观权重

3.3 评价单元的划分

深圳市福田区面积为78.66 km,本次采用正方形网格单元划分法，以1 km×1 km为1单元格，不足1 km的单元格按照就近原则归入邻近单元或者单独作为一个新单元，将研究区共划分79个评价单元,见图4。

图4 研究区评价单元划分图

3.4 评价结果及分析

以图4中标号为7、44、69、73的4个评价单元作为评估样本，根据相关资料，结合有限区间云模型计算公式和指标权重，利用每个单元9个指标的评估值或者实测值计算该评价单元隶属于不同级别的综合确定度，并按照最大隶属度原则，求出不同评价单元地面塌陷的危险性等级，其计算结果见表5。

表5 评估样本地面塌陷的危险性分级

根据综合确定度结果，按照最大隶属度原则，可以得到：评估样本的4个评价单元中，评价单元7的地面塌陷危险性等级处于Ⅰ级，即反映该区域地面塌陷危险性极低；评价单元69的地面塌陷危险性等级处于Ⅱ级，即反映该区域地面塌陷危险性低；评价单元44的地面塌陷危险性等级处于Ⅲ级，即反映该区域地面塌陷危险性中等；评价单元73的地面塌陷危险性等级处于Ⅳ级，即反映该区域地面塌陷危险性高，要注意对该区域进行重点关注，重点防范。

同理，按照上述步骤对剩余的75个评价单元进行计算，其计算结果见图5。

图5 深圳市福田区地面塌陷危险性评价分级图

图5反映了整个研究区域内地面塌陷危险性评价的总体情况，共分为4个等级：Ⅰ级(地面塌陷危险性极低区)、Ⅱ级(地面塌陷危险性低区)、Ⅲ级(地面塌陷危险性中等区)、Ⅳ级(地面塌陷危险性高区)。图6为2013—2019年深圳市福田区地面塌陷数量的统计结果，其中红色表示某次地面塌陷危险性程度高；绿色表示某次地面塌陷危险性程度低。通过比较图5和图6可以发现：研究区地面塌陷危险性程度高的地点，地面塌陷危险性评价等级显示为危险性高区(Ⅳ级)；没有发生过地面塌陷的区域，地面塌陷危险性评价等级显示为危险性极低区(Ⅰ级)；发生多次危险性程度低地面塌陷的区域，地面塌陷危险性评价等级显示为危险性中等区(Ⅲ级)；发生少量危险性程度低地面塌陷的区域，地面塌陷危险性评价等级显示为危险性低区(Ⅱ级)。由此可见，基于有限区间云模型的地面塌陷危险性评价模型是合理的，其评价结果的可信度高。

图6 2013—2019年深圳市福田区地面塌陷数量的统计图

由图5可见，研究区地面塌陷危险性极低区(Ⅰ级)有6个评价单元，面积为5.34 km，面积占比为6.8%，主要分布于福田区西南角以及北部少量开发程度较低区，这些区域受到地面塌陷的危险性极低；研究区地面塌陷危险性低区(Ⅱ级)有38个评价单元，面积为35.07 km，面积占比为44.6%，主要分布于福田区东部、北部区域，南部以及西部区域也有少量分布，这些区域地铁线路和地下管线分布不密集，受到地面塌陷的危险性低；研究区地面塌陷危险性中等区(Ⅲ级)有21个评价单元，面积为22.77 km，面积占比为28.9%，主要分布于福田区中部区域，这些区域地铁线路和地下管线分布较为密集，导致地面塌陷的可能性较大，应对这些区域进行重点关注；研究区地面塌陷危险性高区(Ⅳ级)有14个评价单元，面积为15.47 km，面积占比为19.7%，主要分布于福田区中部以及东南部区域，这些区域地铁线路和地下管线分布密集，且人员密集、施工强度高，导致地面塌陷的可能性大，对这些区域须重点关注，尤其在台风、暴雨等恶劣天气下应加大巡查排查力度，尽量降低地面塌陷造成的人员伤亡和社会经济损失。

4 结 论

(1) 本文根据研究区域内的相关资料，针对地面塌陷危险性评价的不确定性，着重选择了9个影响地面塌陷危险性的不确定性因素建立了评价指标体系，使评价结果更具可靠性。

(2) 采用改进的层次分析法计算指标的权重，一方面降9标度为3标度，以减小人为主观判断模糊性对评价结果的影响；另一方面通过最优传递矩阵构建判断矩阵，可省略一致性检验过程，避免了重复性的计算工作。

(3) 将有限区间云模型方法引入到地面塌陷危险性评价中，用来处理评价指标的模糊性和随机性，从而提高了地面塌陷危险性评价的准确性和客观性，并结合改进的层次分析法计算指标权重，使得评价结果与实际情况更加符合，可为城市地面塌陷的防治工作提供一定的指导。