正弦规成30?时角值误差的测量不确定度评定

马超 董智

【摘要】 本文主要介绍了正弦规成30°角时角度误差的测量不确定度的评定，分析了测量结果不确定度的影响因素。为保障正弦规量值准确可靠提供一种技术手段，对安全生产和高质量制造具有一定指导意义。

【关键词】 正弦规;不确定度

【DOI编码】 10.3969/j.issn.1674-4977.2021.03.012

The Evaluation of Measurement Uncertainty of Angle Error When Sine Gauge is 30?

MA Chao1，DONG Zhi2

（1.Liaoning Institute of Measurement，Shenyang 110004，China;

2.Liaoyang Science and Technology Innovation and Entrepreneurship Service Center，Liaoyang 111000，China）

Abstract： This paper mainly introduces the evaluation of the measurement uncertainty of the angle error when the sine gauge is 30° angle，and analyzes the influencing factors of the uncertainty of the measurement results. It provides a technical means to ensure the accuracy and reliability of the sine gaugevalue，which has certain guiding significance for safe production and high quality manufacturing.

Key words： sine gauge;uncertainty

1 概述

正弦规是利用三角法测量角度的一种精密量具。一般用来测量带有锥度或角度的零件。因其测量结果，是通过直三角形的正弦关系来计算的，所以称为正弦规。它主要由一准确钢制长方体-主体和固定在其两端的两个相同直径的钢圆柱体组成。其两个圆柱体的中心距要求很准确，两圆柱的轴心线距离L一般为100 mm或200 mm两种。本文以测量1级中心距分别为200 mm和100 mm的正弦规为例，在0级平板上对其成30?时的角值误差进行不确定度评定。

2 测量依据

JJG 37-2005《正弦规检定规程》。其中所用00级标准平板在2013年新版检定规程JJG 117-2013《平板检定规程》中已经取消，故采用0级标准平板。

3 测量原理

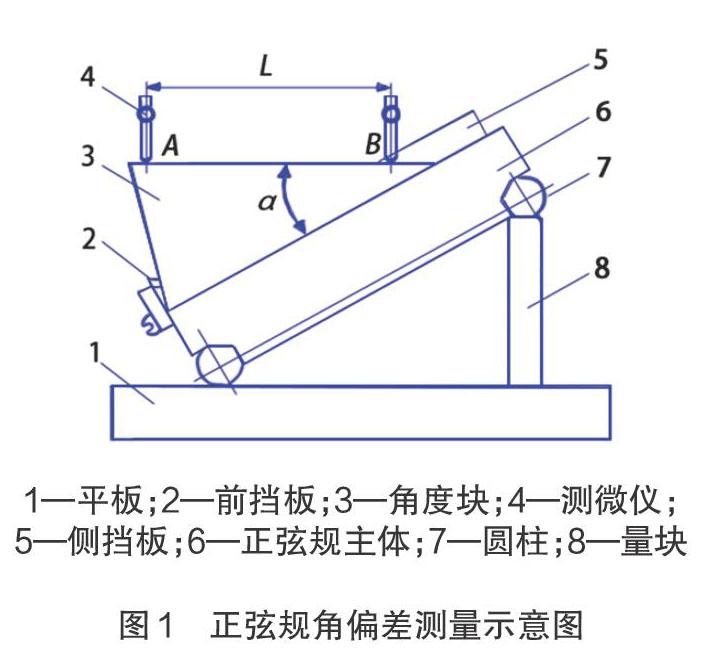
用正弦定理算出正弦规成30°角度时所需要的量块高度，在0级平板上使用量块与正弦规组成30°角度，将30°专用角度块置于正弦规上，并靠紧两挡板，用测微仪测量与角度块接触点A、B两点的数值a和b（使A、B两点间距固定为70 mm），计算二者差值?h，然后通过相关公式计算来确定正弦规的角值偏差的不确定度。

4 数学模型

式中：[Δα]——正弦规角度偏差（"）;

[Δh]——测微仪在A、B两点处测得的高度差（mm）;

[l]——测微仪在测量高度差时A、B两点的距离，本次取固定值70mm;

[L]——正弦规中心距（mm）;

[ΔH]——标准量块的高度偏差值，当[L=200 mm]时，[H=100 mm，]当[L=100 mm]时，[H=50 mm];

[Δi]——标准角度块角度偏差（"）;

n——弧度（rad）到角度的转换系数，[n=180π×3600=206264.81]。

5 数学模型

各输入量互不相关，则由方程[uc2（y）=?f?xi2?u2（xi）]得：

6 标准不确定度分量

6.1 测量[Δh]引入的不确定度分量[u1]

1）测量重复性引入的不确定度分量[u11]（A类评定）

重复性条件下测量A、B两点高度差[Δh]10次结果：4.7、5.0、5.3、5.2、4.8、5.4、5.4、5.0、5.2、4.8 μm。

用贝塞尔公式求得单次测量实验标准差[s]=0.2573 μm，则

2）由测微仪分辨力引入的不确定度分量[u12]（B类评定）

测微仪分辨力为0.1 μm，区间半宽度a=0.05 μm，按均匀分布计算取k=[3]，两次读数取差值：

[u11>u12]，在按贝塞尔方法进行的重复观测中的每一个示值，都无例外地已受到分辨力的影响，为了避免分辨力引入的不確定度的重复计算（二者取较大者），所以此处只考虑由重复性引入的不确定度即可。

3）测微仪示值误差引入的不确定度分量[u13]（B类评定）

测微仪最大允许误差为±0.25 μm，区间半宽度a=0.25 μm，按均匀分布计算取k=[3]：

4）由平板平面度引入的不确定度分量[u14]（B类评定）

JJG 117-2013《平板检定规程》中规定：平板任意250 mm×250 mm局部工作面的平面度允许限：0级平板为3.5 μm。

区间半宽度a=1.75 μm，按均匀分布计算取k=[3]：

6.2 测量[l]引入的不确定度分量[u2]

A、B两点的距离误差为±0.5 mm，服从均匀分布，则

6.3 由标准量块[ΔH]引入的不确定度分量[u3]（B类评定）

6.4 两圆柱中心距[L]测量误差引入的不确定度分量[u4]

两圆柱中心距中心距误差为±0.01 mm，服从均匀分布，则：

6.5 标准角度块角度偏差[Δi]引入的不确定度分量[u5]

标准角度块的不确定度为[U=1]"，[k=2]，则：

7 合成标准不确定度及扩展不确定度

1）当[L=200 mm]时

扩展不确定度：[U=kuc=6.3]"，[k=2]。

2）当[L=100 mm]时

扩展不确定度：[U=kuc=6.3]"，[k=2]。

8 不确定度汇总

不确定度汇总表见表1。

9 结论

正弦规成30?时角值误差的扩展不确定度为：

[U=6.3]"，[k=2]。

【参考文献】

[1] 测量不确定度评定与表示：JJF 1059.1-2012[S].

[2] 正弦规检定规程：JJG 37-2005[S].

[3] 王红敏，石沛林，郑国强.正弦规应用及误差分析[J].山东工程学院学报，2002（4）：61-64.

【作者简介】

马超（1992-），男，助理工程师，学士，研究方向为几何量计量。

董智（1965-），男，工程师，学士。