基于最优停止理论的网络欺骗防御策略优化

吕德龙，翁 溪，周小为

(1.陆军工程大学 指挥控制工程学院，江苏 南京210007；2.江南计算技术研究所，江苏 无锡214083)

0 引言

近年来，网络攻击的数量和复杂性都在迅速增加[1-2]，攻击者能够利用多种攻击载体(如零日漏洞、软件配置中的缺陷和访问控制策略等)渗透到其目标系统中。针对上述问题，研究人员提出了许多解决办法来增强网络和信息系统的安全防护能力，典型的解决方案包括入侵防护[3]、系统加固[4]以及高级攻击检测和缓解等[5]。尽管这些传统的安全措施在任何安全防护手段中都必不可少，但它们大多被动响应攻击者的行为，缺乏在网络杀伤链的早期就与攻击者进行交互的手段，导致防御方始终处于被动地位。

网络欺骗防御技术是为改变防御方被动地位解决攻防不对称问题[6]而引入的新思路，网络欺骗防御技术通过在攻击者必经之路上构造陷阱，混淆其攻击目标，使得攻击者难以辨别信息系统外显特征真假，陷入虚假系统探测和攻击中，增加攻击成本和代价，而且在受控的环境中可以记录并追溯攻击者的行为，最终实现保护网络内部的真实资产的目标。

但是，防御者诱骗攻击者的过程中也可能会被攻击者获取到过多的真实网络特征，如何在有效地迷惑住对手的同时，确保信息收益最大化是亟需解决的一大问题。为解决此问题，本文结合欺骗防御和最优停止理论，从防御者视角考虑，基于最优停止理论，求解防御方最佳抑制攻击时刻，实现最大化防御系统收益的目标。

1 相关工作

20世纪80年代末，斯托尔[7]首次讨论了如何利用欺骗技术来跟踪入侵者，以确保计算机安全，并在此基础上形成了蜜罐的概念。为了吸引潜在的攻击者，蜜罐把自己伪装成可能被利用的服务主机，通过收集和记录攻击者破坏蜜罐的方法，防御方可以使用学习到的知识来增强系统安全性。近年来，出现了不少利用欺骗技术[8-10]来迷惑或误导攻击者的技术手段。网络欺骗防御技术可用于保护易受攻击的业务系统，并因其自身的优势而受到了安全防御人员的关注。欺骗的概念在几乎所有安全领域都以不同的形式出现，但欺骗防御技术一般是指在攻击者与目标系统交互时用作防御机制来欺骗攻击者的技术。

欺骗防御不是在发现入侵者后，立刻驱逐攻击者，而是使用构建好的诱饵动作来响应攻击者，例如虚假协议消息[11]、响应延迟[12]、诱饵消息[13]等。在法国总统大选期间，马克龙的团队被曝利用伪造文件创建了大量的虚假账户[14]，并将其与大量虚假信息混淆。通过将这些账户主动暴露给攻击者，成功防御了网络钓鱼攻击等网络攻击手段。

文献[15]构建了基于陷阱的体系，防御方对监控密码、身份验证cookie、信用卡和文件等敏感数据进行修改、重放等操作后作为诱饵数据注入到系统中，诱发攻击者主动攻击，使得攻击者暴露。不过此时又出现了新的问题，即释放敏感数据的标准是什么，何时停止释放才能在取得最大收益的同时付出最小的代价。

对于网络欺骗策略的决策问题，目前有多种解决方案，文献[16]将决策问题建模为微分对策，从而得到网络欺骗的动态策略。文献[17]对攻击者和防御者之间的相互作用进行了博弈理论的研究，利用不完全信息的非合作二人动态博弈模型来模拟防御者和攻击者之间的交互，确定符合完美贝叶斯均衡的策略即为最佳策略。

针对网络欺骗防御的决策问题，本文引入了最优停止理论，最优停止理论在网络领域已经有了很好的应用，如黄羡飞[18]、彭颖[19]等人利用最优停止理论解决了无线网络中的数据传输效率问题。网络欺骗防御过程中的行为是随着时间变化的，该特点与最优停止理论是符合的，因此本文将欺骗防御过程中策略优化问题转变为最优停止问题的求解。

2 背景及问题描述

2.1 系统模型

在网络欺骗防御系统中，为了尽可能地欺骗对手，防御者需要在欺骗过程中适当放置一些真实的、敏感的信息，让对手误以为防御方没有检测到他们的行动进而继续对诱饵数据或在诱捕环境内攻击。本文研究防御方在已知攻击者的情况下，在满足防御总目标的前提下，如何使平均信息泄露量最小化。

在网络攻防中，可以将攻击者的攻击细化为单个行动。攻击者的每次行动都会对防御系统产生影响。攻击者每发起一次攻击行动，防御方就可以通过欺骗系统获取到该攻击行动所窃取到的有用信息，即泄露的真实信息。假设欺骗系统可以对每次攻击进行分析得到其攻击相关信息量为A，以及对应泄露的真实信息量L。防御者需要在一轮攻击中确定一个合适的时刻来抑制后续攻击行动，以确保自身利益最大化。一轮攻击防御过程如图1所示，若防御者未能选出最优抑制时刻，将会遭受攻击者的完整攻击。

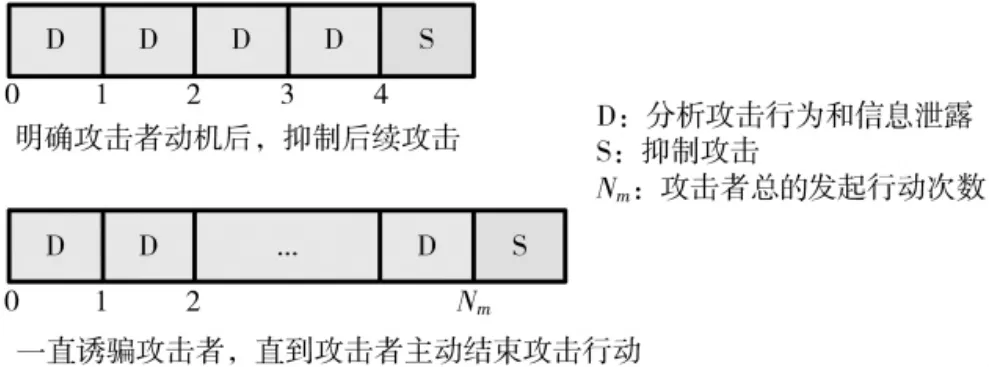
图1 一轮攻击防御过程

2.2 最优停止理论

最优停止理论是一个一般的数学模型，让决策者可以在一个由时间或数量组成的随机序列中，在合适的时刻做出相应的决策行为，实现获取最大的收益或付出最小的代价目标。最优停止理论问题有如下对象定义：

(1)随机变量X1，X2，…，并假设变量服从联合分布；

(2)实值报酬或成本函数序列：y0，y1(x1)，y2(x1，x2)，…，y∞(x1，x2…)。

相关联的停止规则是：在观察到X1=x1，X2=x2，…，Xn=xn(n=1，2，…)后，决策者选择停止观察并接受已知收益或代价函数yn(x1，…，xn)，或者继续观察Xn+1。图2展示了收益或代价函数Y随随机变量X的变化过程，其中，YN=yN(x1，…，xN)是表示在N时刻的收益或代价。如果不进行任何观察，决策者接受y0；如果不停止观察，决策者接受y∞(x1，x2，…)。这个策略可以使决策者在最优停止时刻N(0≤N≤∞)得到最大化期望收益E[YN]或最小化期望代价E[YN]。其中，E[]表示期望值。当n→∞，该最优停止问题则为无限范围的问题。但在实际中，n的值一般不会超过最大值Nm，此时该问题变成有限范围问题，它是无限范围问题的特殊情况，可进行反向归纳的方法求解，即从最大值Nm向最小值0进行反向计算。

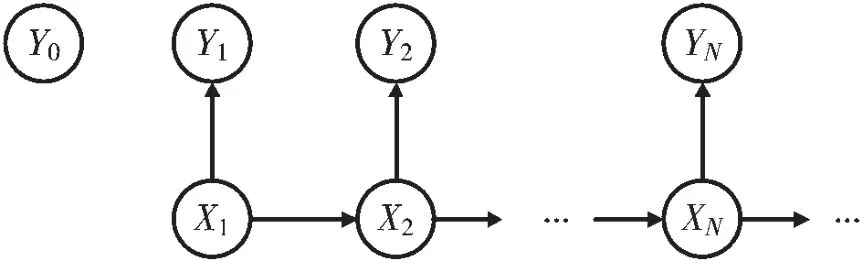
图2 最优停止问题流程图

2.3 网络欺骗防御的最优停止理论问题

在欺骗防御过程中，防御者既需要为部分攻击行为释放真实信息来引诱对手持续发起攻击直到主动驱逐攻击者，又需要尽可能少地泄露真实的信息。防御者可以通过欺骗系统持续观察攻击者的行为，并计算出攻击行为所暴露出的信息，同时计算出该攻击行为所窃取到的真实信息量。通过观察的结果选择最优时刻抑制攻击，以使信息收益最大化。因此该欺骗防御问题可转换为一个有限范围的最优停止问题。

在网络攻防中，攻击者的一次攻击包含多个操作行为，同时为了迷惑防御方，会对各攻击行为进行混淆，使防御方不能简单快速识别攻击。对于防御方，为了尽可能获取到更多的攻击特征信息，需要适当给攻击者透露一些有效信息以激励攻击者做出进一步动作。同时，防御方不能无止境地泄露真实信息，泄露过多会带来巨大安全隐患。因此，防御方通过对攻防信息的获取，选择最优时刻停止观察并抑制后续的攻击行为，以使获取到的总攻击信息与泄露的总的真实信息量之比最大化，这是一个最优停止策略问题。图3展示了网络欺骗问题和最优停止问题的各要素对应关系。

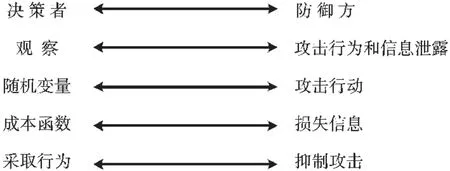
图3 问题要素对应关系

3 欺骗防御优化策略

3.1 信息收益最大化问题的构建

在欺骗防御中，攻击方进行第n次攻击时，定义观察到的变量序列为Xn={An，Ln}，其中An表示攻击者在第n次攻击时所暴露的信息量，Ln表示欺骗防御系统在第n次攻击时所泄露的信息量。攻击行为信息量的度量可以根据攻击行为类型进行量化，即计算一次攻击中所包含的各个行为所对应攻击目的的概率。即攻击行动an对应的攻击信息量计算公式为：

同样，泄露真实信息量则根据防御者在应对攻击时所使用的真实信息的重要性进行度量。即攻击行动an所造成的真实信息泄露量为：

假设对一个目标的攻击一共包含M次行动，N为防御者抑制后续攻击行动的时刻，则有1≤n≤N≤M。由此可知，第n次行动后攻击者所暴露的信息总量为，防御方泄露的真实信息量为那么，由攻击信息总和与泄露信息总和相比可得表达式：

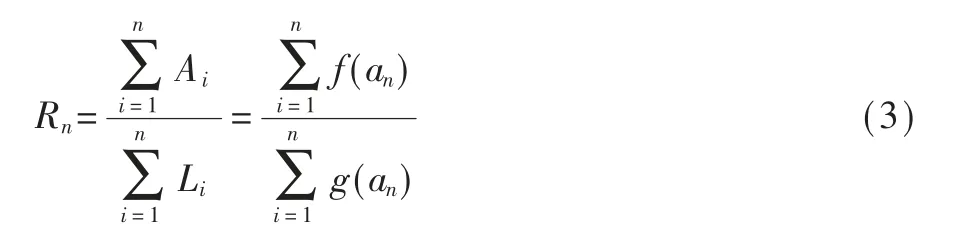
即需要根据式(3)确定如何获取最大的信息比。

3.2 信息收益最大化问题的求解

可以利用式(3)将如何获取最大的信息比Rn转换成一个面试问题。面试问题是如何在M个面试者中找出最优秀者，即如何在这M次攻击中找到最大信息比。首先需要按照秘书问题来给定一个随机变量yk(1≤k≤M)表示RN的绝对排名，当yk=1时，表示在第k次观察时得到的RN在M次观察中最优。由于本文的攻击-欺骗过程是不可逆的，因此还要再给定一个随机变量xj(1≤j≤k)来表示RN的相对排名，当xj=1时表示第j次侦测的RN在相对观察次数k中最优。如果要使得第k次侦测的RN在xj是最优值，可以得到第k次观察时RN在xj的概率为：

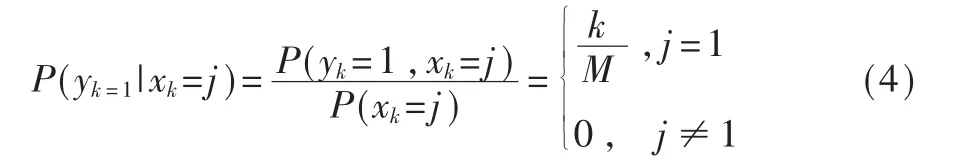
对于r=1，…，M，有以下停止规则ξ(r)存在：前r-1次攻击行动都不作出抑制，然后对剩下的M-r+1次的攻击进行侦测分析，如果任何一次攻击后的攻击信息和与泄露信息和比值都比之前要大，那么就在此次攻击动作之后抑制后续攻击动作。前r-1次攻击被选中的概率为0，假设从第r次攻击开始，侦测到第k次攻击时信息量比值最大且被选中作为抑制后续攻击的点，那么最大值被选中的概率为：

其中，第k次作为信息量比最大值并且被选中的攻击，根据概率论的知识，可以化简为：第k次攻击在最大值的前提下被选择。因为最大值只有一个，所以它的概率为1/M。既然是最大值，那么最大值对应的攻击行为被选择的概率大于其前后攻击被选中的概率，所以有：

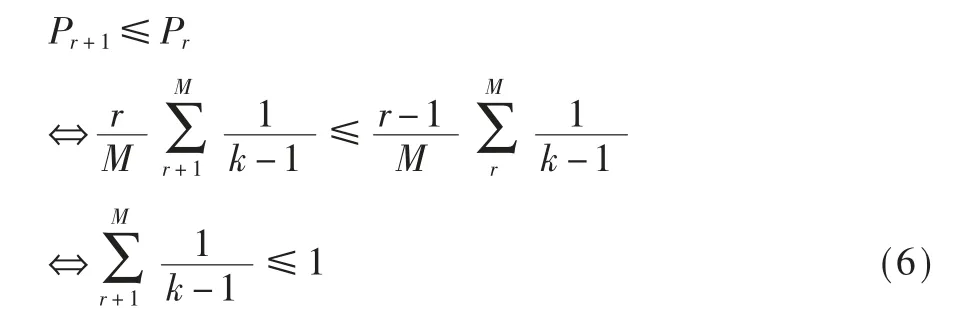
得到r的一般表达式，现要找出最优解，等价于找到满足以下条件最小的r值：

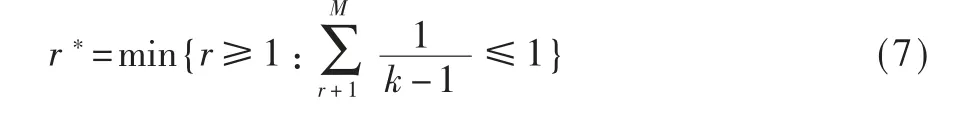
4 结论

网络欺骗防御是网络主动防御的重要手段，但传统的欺骗防御策略往往侧重于如何更好地引诱攻击者进行攻击，直至耗尽攻击者的攻击手段，而忽视了泄露过多信息可能带来的安全隐患。为此，本文针对网络欺骗防御系统中防守方的最佳抑制攻击时刻的选择进行了分析，发现在攻击信息量和与泄露信息量和之比的最大值时刻抑制对手后续攻击，可使防御方的利益最大化。本文基于最优停止理论构建了信息最大化收益问题模型，并做出了相应假设和数学推导，求解出最优解表达式。后续工作会根据不同攻击行动的分布模型，建立完备的信息量评价机制，同时对该最优停止理论模型进行实验评估。