初探旋转的工具作用

钟晓鸣

◆摘  要：在初中几何中有很许多的问题可以用旋转来解答。本文用旋转三种角度解决问题，进而呈现旋转的工具作用。在教学过程中向学生阐述旋转的工具性，培养学生的解题素养，使学生有的放矢，解答中往往可以起到事半功倍的效果。

◆关键词：旋转;变换;工具

图形的旋转是初中数学图形运动（变换）的第三种形式。它是认识刻画图形位置形状的一种方法。因此旋转图形是一种方法，是一种技巧，更是一种工具。旋转在平面几何中有广泛的应用，因此在教学中向学生阐明它的工具作用，培养学生使用旋转来解决问题的思维方法，进而问题得以简解。

一、旋转的定义

在平面内，把一个图形绕点O旋转一个角度的图形变换叫做旋转，点O叫做旋转中心，旋转的角叫做旋转角，如果图形上的点P经过旋转变为点P，那么这两个点叫做这个旋转的对应点。

二、旋转的性质

①对应点到旋转中心的距离相等（意味着：旋转中心在对应点所连线段的垂直平分线上）。②对应点与旋转中心所连线段的夹角等于旋转角。 ③旋转前、后的图形全等。

三、下面例举用旋转作为工具来解题、证题加以说明

（一）题目中出现有线段的中点，可以旋转1800来解答。

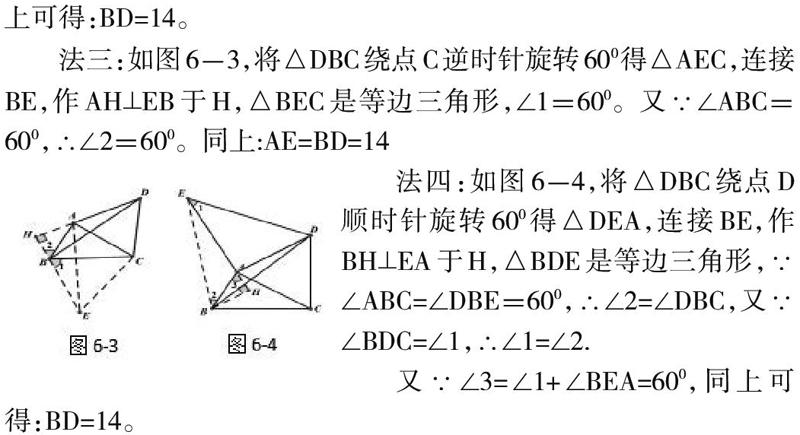
旋转600就会出现一个等边三角形和一对全等三角形，使求角度、线段等问题得以简解。

对于学生而言，只有具备充分的旋转的数学体验和经验，才能有意识地运用图形旋转这种工具来解决一些平面几何中的问题。

笔者认为，在教学旋转内容时，要切实让学生把握两点要求：一要充分理解旋转的情况下，几何元素中的变化量和不变量;二要懂得旋转是一种工具，是解决几何问题是可以运用的利器;旋转 600出现等边三角形，旋转900出现等腰直角三角形，旋转1800出现中心对称。通过旋转有了特殊图形，使得问题柳暗花明。因此，有了旋转这个实用的工具，使得一些几何问题得于简解。所以，在教學中向学生阐明旋转的工具作用是很在意义！

参考文献

[1]刘清泉.旋转变换与解题，几何证题.中学数学研究，2014（05）.

[2]黄永新.巧用旋转变换解初中几何问题.中学教学参考，2018（01）.