热风炉出风嘴优化设计
林 杉,高 文,尹识谋,夏 晶
(中国电科第43研究所-合肥恒力装备有限公司,安徽 合肥 230031)
0 引言
热风炉进出口结构、加热件热物性对于加热件本身升温速度和温度均匀性有着明显影响。利用仿真软件建立热风炉数值模型,并用试验结果进行校验。通过数值模型分析不同工况下加热件的温度变化情况和炉体内流场分布,为热风炉出风嘴的设计方案提供参考[1]。
1 模型建立
1.1 物理模型
环境条件如图1所示。
炉内起始温度为500℃,产品起始温度为100℃;热风从上往下吹,温度 500℃,风速 10 m/s;加热件为陶瓷材料,热物性见表1。

表1 加热件热物性参数表Tab.1 Heater thermal property parameter table
加热体从上至下存在方形孔,网格尺寸1.5 mm×1.5 mm,壁厚0.2 mm。加热件导热率未知,通过条件1下的试验结果进行校验,试验结果如图2。
为了方便叙述,将升温曲线分为三段。以测温点3为例,试验开始时,热量还未传导至测温点,该点温度基本不变,为起步段;当热流来向的加热件温度升高以后,测温点3得热增多,温度快速上升,为上升段;当温度较高以后,测温点3得热减少,温度变化减缓,缓慢上升至500℃,为稳定段[3]。利用校验后的模型仿真不同条件下,加热件的温度变化情况和炉体内流场分布,不同工况如下图3所示。
模型中加热件为分布均匀的实心固体,孔隙对传热的影响通过改变热物性及边界条件模拟。针对热风炉建模并划分网格,由于加热体周围温度梯度大[4],流场变化快,针对加热体附近网格进行加密,如图4所示。
加热件轴向即为计算域的Y向,径向在计算域X0Z平面上。
1.2 物性参数及边界条件
(1)比热容
加热件为多孔结构,孔边长 1.5 mm,壁厚0.2 mm,孔隙率 75%左右;堇青石比热容约为1000 J/kg*K,考虑到加热件两头孔隙率更小,等效比热容取300 J/kg*K。
(2)加热件边界条件
加热件侧面为光滑表面,不做特殊处理;加热件上表面有气流通过,加热件上表面通过的热流包括对流传热及气流带入的热量,所以上表面等效对流传热系数应远大于实际对流传热系数,通过拟合曲线确定等效对流传热系数[5]。加热体下表面为热风尾流,加上底部风扇,传热系数较小。
以输入参数的条件 1为例,通过调整参数确定各面等效传热系数,见表 2;其他条件的传热系数以条件1参数为基础随工况变化。

表2 条件1加热件各面传热系数Tab.2 Condition 1 heat transfer coefficient on each side of heating element
(3)导热率
考虑多孔材料的特性,加热件的径向和轴向导热率取不同值:径向取空气和材料的等效导热率;轴向上考虑材料、空气的等效导热率以及气流流动的传热。
2 验证模型—条件1
针对多孔材料特性建立导热率各向异性且随温度变化的模型,导热率详情如下。

表3 轴向(y方向)导热率随温度变化情况Tab.3 Axial (y direction) thermal conductivity changes with temperature
400℃—500℃之间,需要考虑气流流动及陶瓷烧结完成时的热物性变化,导热率变化较大,确定导热率的迭代过程。利用确定好的参数体系仿真条件1的工况下加热件温度变化曲线[6]。
2.1 温度场仿真结果
不同时间点炉内温度分布如下图5所示,产品的中心温度随着时间的推移越接近炉内温度,在18 min左右接近于炉内温度。
2.2 风速场仿真结果
T=10 min,炉体内风速矢量及风速云图如图6和图7。
3 验证结果
T=5 min时,测温点1温度为475℃,T=10 min时,测温点2温度为450℃,T=18 min时,测温点3温度为500℃。测温点1、2、3到达450℃的时间分别为1.15 min、10.48 min及12.12 min。
仿真模型与试验结果主要差距为:仿真中,温度点1在初始段缓慢变化的过程很短,与试验结果不符,可能是材料存在结晶水等气化吸热,温度变化较慢。加热过程中,各测温点之间、测温点与气流之间均存在温差,无法在加热过程中达到 500℃,各点到达稳定温度的时间与试验结果不同[7]。
利用模型仿真不同条件下各测温点温度变化曲线,得到各点到达450℃的时间,如下表4所示。
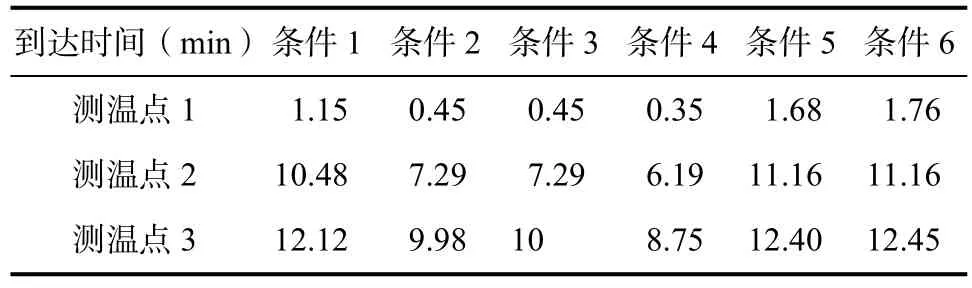
表4 各测温点到达450℃时间Fig.4 Time for each temperature measurement point to reach 450℃
4 结论
六种工况中,条件4中各点升温速度最快。仿真结果表明,通过改变出风嘴风道,将气流集中后射向加热件上端面的中心点附近,可以有效提升加热速率。对热风炉腔体的设计提供了有效参考。

