基于USLE的大豆C因子计算模型研究*

徐 宁，杨一凡，林青涛，谢欣利，吴发启

（1.西北农林科技大学水土保持研究所，陕西杨凌 712100；2. 西北农林科技大学资源环境学院，陕西杨凌 712100）

作物覆盖与管理对土壤侵蚀的影响通常用C表示，它来自于美国通用流失方程（USLE），USLE对C定义为有植被覆盖或实施田间管理的土壤流失量与同等条件下清耕休闲地上的土壤流失量之比。USLE中C因子的计算主要考虑了作物的生长阶段和降雨侵蚀力两个因素，即：作物每个生长阶段的值与该作物同一生长阶段所具有的R值占全年R值百分数乘积的总和[1]。1965年版USLE[2]划分5个农作期计算C值，1978年版USLE[3]划分了6个农作期且增加了适用于水土保持耕作法的土壤流失比率表。在观测数据的基础上，USLE手册给出了主要农作物和耕作制度下的土壤流失比率表，年平均C值需根据降雨侵蚀力年内季节分布进行加权计算。RUSLE则采取了与之完全不同的次因子法，不再使用基于观测数据的土壤流失率表，也不再划分农作期而是以15 d为步长计算半月土壤流失率。RUSLE1中土壤流失率（SLR）计算主要考虑5个次因子，即前期土地利用次因子（PLU）、冠层覆盖次因子（CC）、地面覆盖次因子（SC）、地表糙度次因子（SR）和土壤水分次因子（SM）等，每个次因子均有具体计算公式，使C值的计算更加科学合理[4]。RUSLE2中将C因子的计算步长缩短至每天，次因子数量由5个增加至8个，次因子的计算公式也更加细化，考虑了植被覆盖和管理对细沟侵蚀和细沟间侵蚀的影响。在美国最新一代水蚀预报模型（WEEP）中，C因子考虑得更为详细，分散在土壤模块、植物生长模块和残留分解模块等子模块中[5]。80年代初USLE被引入我国后，国内学者开始对USLE在中国的应用开展了广泛研究。总体来看，C因子计算主要有手册查询法、标准小区法、次因子法、反算法和盖度法等。与美国相比，我国基于作物各生长阶段土壤流失比率计算C值的径流小区资料相对匮乏，难以通过土壤流失率直接计算C值，符合要求的小区资料就更少，因此出现了大量利用植被覆盖度估算C值的方法。

植被的存在能增加土壤入渗、减少径流与流速、提高土壤抗蚀性与抗冲性[6]。有研究表明植被覆盖度与径流量、土壤流失量之间存在较强的相关性[7-8]。如Mayor等[9]在坡面和流域尺度上植被阻蚀减沙效应的研究中指出，侵蚀产沙总体随植被盖度增加而减少；Gao等[10]在对坡面植被盖度与水土流失关系的研究中发现，植被盖度越高，其降低径流含沙率的作用就越明显。目前利用植被覆盖度估算C值是C值计算的主要方法之一。针对农作物的植被覆盖度估算C值，刘宝元等[11]、刘秉正等[12]、蔡崇法等[13]、马波等[14]均给出了不同计算公式，但是覆盖度仅能体现出作物覆盖这一方面，未体现出C因子定义中的管理因素，如结皮、糙度等反映土壤地表结构与微地形态的因子。并且植被覆盖度也不是唯一影响土壤侵蚀的因素，作物的高度也会影响雨滴的溅蚀。植被枝叶和主干仅能拦截部分降雨量，还有一部分降雨量在枝叶上形成大水滴落向地面，可对地表形成较大的雨滴击溅侵蚀[15]。蔡强国等[16]认为植被覆盖度和株高在防止土壤侵蚀与溅蚀产沙过程中有着重要作用，株高的增加以及与植被覆盖度的交互作用，使植被覆盖对侵蚀的保护作用减弱。Sreenivas等[17]研究发现作物冠下溅蚀量随作物冠层距地面高度的增加而增加，随冠层覆盖度的增加而减少，因此冠层越密，高度越低的作物溅蚀量越少。由此可见，株高在土壤侵蚀产沙研究中的影响作用不可忽视。Schiettecatte等[18]利用RUSLE模型研究玉米-烟草轮作与玉米-大豆间作等对C值的影响中发现，豆科植物的作物冠层高度小，且生育期短，能在较短时间内增加作物冠层覆盖度，因此大豆-玉米间作C值（0.369）较烟草-玉米轮作C值（0.478）小，可有效减少土壤流失量。刘宝元等[11]将株高纳入了C值计算，综合构建北京土壤流失方程。

土壤结皮作为一种特殊的土壤下垫面，其表面强度大，孔隙较细且导水性较差，能够减少入渗，促进地表径流，降低作物生物量和产量，影响坡面产沙[19]。土壤结皮对地表径流有促进作用，这是目前大家一致认同的观点。然而，土壤结皮是否对坡面产沙也有促进作用还存在争议。吴发启和范文波[20]研究认为前期土壤结皮的存在使得坡面径流量增加但产沙量却降低。然而，蔡强国等[16]研究认为坡耕地前期有土壤结皮时，地表更容易形成径流，更易发生侵蚀产沙。由此可见，虽然土壤结皮对地表径流有促进作用的同时对侵蚀产沙是否有促进作用还存在较大争议，但其影响程度对于侵蚀产沙而言不容忽视。C因子计算模型的发展过程中，WEEP模型[5]在土壤模块的水文参数和土壤分离参数中均有考虑结皮因子。因此，可将结皮因子纳入C值计算，进一步完善C因子的计算模型。

地表糙度是在耕作活动下土壤重新分布，形成高低起伏、凹凸不平的微地形结构。地表糙度具有增加土壤入渗、减缓坡面径流产生和削弱径流能量的作用，并且很多土壤侵蚀预报模型如WEEP等均将地表糙度作为重要参数之一。但目前针对地表糙度对坡面土壤侵蚀作用的认识还不够全面，一般认为土壤流失量与地表粗糙度存在反比例关系，即地表粗糙度具有减少坡面土壤侵蚀的作用。地表粗糙度能够通过影响径流而影响产沙，即通过减少坡面径流量进而减少侵蚀量[21]。有学者认为增大地表糙度会增大径流阻力，使径流流速变缓，降低径流剪切力，侵蚀作用减弱[22]。也有学者认为地表粗糙度会引起地表径流的集中或分散，而径流的集中会造成局部侵蚀量的增加，在这种情况下，粗糙地表土壤侵蚀的增加归因于地表径流的集中[23]。因此，研究地表糙度对侵蚀产沙及C因子计算有重要意义。

综上，植被覆盖度只是表征地表作物覆盖的指标之一，并不能体现管理措施对土壤流失的影响。因此，本研究以大豆为研究对象，通过室外人工模拟降雨，以植被覆盖度作为关键因子，以株高、结皮厚度、地表糙度作为调节因子逼近误差，使得模型计算的C值与实测C值间的误差不断减小，建立大豆植株在不同生育期的C因子计算模型，以期为黄土高原农耕地C因子计算模型的深化研究及不断完善提供理论依据和科学参考。

1 材料与方法

1.1 研究区概况

试验地点位于陕西省黄土高原南部（34°14′～34°20′ N，107°59′～108°08′ E），海拔高度为468 m，属于半湿润大陆性季风气候，年平均降水量635～646 mm，年平均蒸发量为993 mm，大约60%～70%的降水发生在7—9月。黄土高原典型的黄土地貌分为谷间地地貌和沟谷地貌，坡度大多介于24.9%（13.98°）～53.2%（28.01°）。主要土壤类型为塿土，是当地森林褐土经长期施加土肥以及农业耕作所逐渐形成的特殊耕作土壤。

表1 研究区土壤的基本理化性状Table 1 Physical and chemical properties of the soil in the study

1.2 试验设计

室外模拟降雨试验于西北农林科技大学水土保持与荒漠化防治教学实验基地的径流小区上进行。采取中国科学院水土保持研究所制造的侧喷式组合降雨模拟器进行试验。降雨模拟器的侧式喷头高为6 m，安装于由三脚架固定的降雨支架上，两侧喷头座架距离为7 m，降雨高度为7.5 m，有效降雨面积为35 m²。可通过压力表调节供水压力进而控制降雨强度。径流小区规格为4 m×1 m，设置小区坡度为10°，为我国采用的的标准小区坡度[24]。供试品种为大豆（中黄13），大豆株行距为20 cm×40 cm。由于该地区夏季多大到暴雨[25]，因此设置降雨强度为80 mm·h-1。为避免天然降雨对试验结果产生影响，天然降雨时，所有小区均需进行遮盖处理。

该试验共设置3组重复，在径流小区坡面进行作物+糙度+结皮处理，10°裸坡作为对照。降雨试验开始前对所有小区进行统一翻耕与整平，种植作物小区在翻耕整平的地表上按照当地农作习惯进行锄耕后，再通过预降雨在有糙度地表上产生结皮，使地表处于结皮与糙度共存。其中，根据前期试验，发现在降雨强度为40 mm·h-1，降雨时间为15 min，降雨量达到10 mm时，可在地表形成一定特征结皮，满足试验实施。大豆播种时间及后续田间管理均参考黄土高原大田实际情况进行，播种前进行翻耕整地并施加有机肥。并且依据大豆生长、叶片的面积及数量将大豆全生育期划分为五个生育期（幼苗期、始花期、盛花期、结荚期及始粒期）。

1.3 参数测定

产沙量的测定：降雨开始后，观察径流小区出口处水流呈连续流出状态时，即为产流开始，此时对应的时间为产流开始时间。从小区产流开始，在径流小区出口处用塑料小桶每3 min收集径流和泥沙样品1 min，直至产流结束。降雨历时1 h，将收集的径流样本静置24 h后倒掉上清液，将沉淀的泥沙样品在105℃下烘干称得重量即为产沙量。

植被覆盖度的测定：借助Image J软件通过“照相法”测量植被覆盖度[26]。首先距离地表3 m垂直地面进行拍照，再借助Image J软件将彩色图转化为灰度图，提取所拍照片上的植被像素点。照片中植被像素点与总像素点的比值即为植被覆盖度。

株高的测定：定苗后，在每次降雨试验前，任选5～10株大豆，用卷尺测定其顶端至地面的距离，取其平均值即为株高。

结皮厚度的测定：在径流小区的不同部位随机收集10块结皮样本，用游标卡尺测量其厚度，样本厚度的均值即为结皮厚度。

地表糙度的测定：利用“链条法”测定地表糙度[27]。链条原长为0.9 m，由于粗糙地表形态有起伏，因此链条紧贴地表会有明显缩短。地表糙度计算公式如下：

式中，Cγ表示地表糙度，无量纲；L1表示链条原长，m；L2表示放置地表之后链条两端的直线距离，m。

1.4 C值计算

基于实测值的C值计算。根据USLE的定义，C值为有植被覆盖或实施田间管理的土壤流失量与同等条件下清耕休闲地上的土壤流失量之比。本研究通过室外人工模拟降雨可观测得到种植大豆小区与对照裸地小区的土壤流失量，进而计算C值。计算公式为：

式中，A为土壤流失量，g·m-2。

基于植被覆盖度的C值计算。在充分搜集和学习相关文献的基础上，对于不同生育期大豆C因子值的计算选取刘秉正等[12]、蔡崇法等[13]以及刘宝元等[11]的计算公式。其中，刘秉正等及蔡崇法等的计算公式仅包含植被覆盖度这一个自变量，而刘宝元等公式不仅包括植被覆盖度，也将株高纳入其中。

刘秉正等[12]定义了“植被保土作用系数”的概念，并且根据收集的西峰、淳化两地17个径流小区有关侵蚀与植被覆盖的资料，通过计算发现，C值仅与作物覆盖度有关，与其他因素无关，建立了利用覆盖度估算C值的对数关系式：

式中，V为作物覆盖度，%。

蔡崇法等[13]利用径流小区人工降雨以及一部分天然降雨观测资料，通过计算坡面产沙量以及植被覆盖度之间的相关关系，建立了C因子与植被覆盖度的对数关系式：

式中，V为某生长季作物或者植物的覆盖度，%。

与一般C因子与植被覆盖度的关系式不同，刘宝元等[11]考虑了群落层次结构。其研究综合考虑了地表作物高度、冠层覆盖度以及地表覆盖度的影响，利用人工降雨试验和径流小区观测资料建立北京土壤流失方程。将C因子分解为两个子因子：冠层覆盖子因子和地表覆盖子因子。

式中，CC为冠层覆盖子因子，无量纲；CS为地表覆盖子因子，无量纲；VC为作物冠层覆盖度，%；h为冠层高度，cm；VR为地表枯落物覆盖度，%。

1.5 模型构建

加入关键因子模型。植被覆盖因子作为关键因子，已有众多学者研究得出了其与C值间不同类型的关系式，将植被覆盖度代入各学者公式中得出预测C值，与实测C值进行作图对比并计算其均方根误差，选取与实测C值曲线最接近、均方根误差最小的公式，以其含植被覆盖度因子的因式函数类型及系数作为本研究模型中关键因子即盖度与C值间的函数类型及系数。

加入调节因子模型。关键因子（植被覆盖度）加入模型的形式确定后，记为因式A。将调节因子（株高、结皮厚度、地表糙度）加入模型以减小模型误差。首先将植被覆盖度代入因式A，得到一组数据（数据集a）。再进行两个处理：（1）将数据集a与实测C值做差，将这组差值作为误差项。误差项作为因变量，结皮、糙度和株高因子作为自变量，进行回归分析，得到此误差项与结皮、糙度和株高之间的最佳拟合公式。（2）将数据集a与实测C值相除，将这组商值作为误差项。误差项作为因变量，结皮、糙度和株高因子作为自变量，进行回归分析，得到此误差项与结皮、糙度和株高之间的最佳拟合公式。

最后通过计算均方根误差（Root-meansquare-error，RMSE）来对比分析两种处理得到的C因子估算模型的精度。

2 结 果

2.1 实测C值

大豆不同生育期植被覆盖度、株高、结皮厚度、地表糙度变化特征以及不同生育期基于实测数据计算的C值见表2。表2数据表明，随着大豆的生长，植被覆盖度和株高均显著增加；结皮厚度从始花期开始显著增加，幼苗期和始花期无显著差异；地表糙度则呈现先减小后增大的趋势。大豆对泥沙的拦截作用随其生长发育逐渐递增，种植大豆的作物小区产沙量从幼苗期到始粒期减少80.01%，从始花期开始显著减少。表中C值随着大豆的生长发育呈逐渐减小趋势，也反映了作物保土减沙作用的逐渐增强。

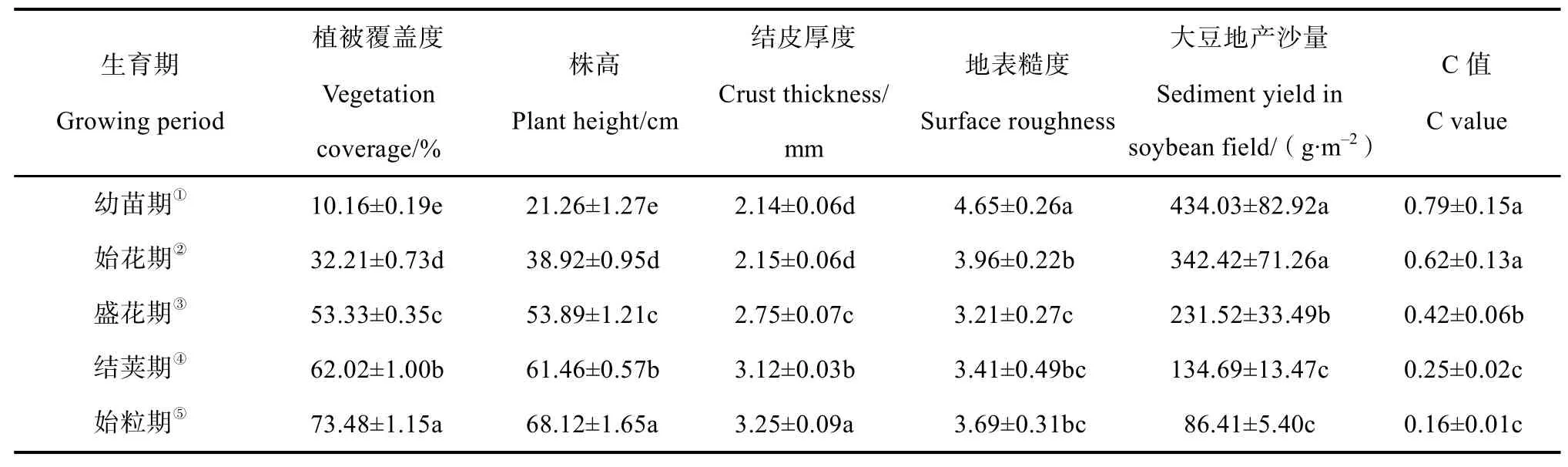
表2 各指标及C值变化特征Table 2 Variation of C with each index

2.2 植被覆盖度的C因子模型

将大豆不同生育期的植被覆盖度代入刘秉正、蔡崇法以及刘宝元的计算公式，其中刘宝元还将株高纳入了C值计算，将其一并代入公式中，得到对应计算公式下的C值，将其与实测C值进行对比，见图1。

从图1可知，刘秉正、刘宝元及蔡崇法公式计算所得C值变化趋势相同，均随植被覆盖度的增加呈减小趋势。由于几位学者研究的地域及作物种类之间有差别，且通过软件在拟合过程中也存在一定误差，因此各学者公式计算所得C值与实测C值均有不同程度的误差，这是难以避免的。其中刘秉正计算公式所得C值与本试验实测C值更为接近。此外，计算RMSE来对比三位学者计算公式所得C值与实测C值的偏差程度，蔡崇法为0.37，刘宝元为0.14，刘秉正为0.12。

由于本试验实测C值曲线与刘秉正公式拟合的曲线（图1）最为接近，且RMSE最小，因此以刘秉正公式含植被覆盖度因子的因式函数类型及系数作为本研究模型关键因子（植被覆盖度）加入模型的基本形式。即为刘秉正公式剔除常数项得到的C值与植被覆盖度间的模型：

式中，V为植被覆盖度，%。

2.3 加入调节因子的C因子模型

采用将调节因子加入模型的两种处理方法，将结皮厚度、地表糙度和株高加入模型，结果如下：

式中，1Δ表示将植被覆盖度代入式（6）中得到的C值与实测C值相减得到的的差值误差项；Δ2表示将植被覆盖度代入式（6）中得到的C值与实测C值相除得到的比值误差项；x1表示结皮厚度，mm；x2表示地表糙度，无量纲；h表示株高，cm。

通过以上两个处理得到的误差公式与前面包含植被覆盖度的因式结合起来，得到两种处理下的不同C因子计算模型（表3）。

2.4 两种模型精度评价

两种处理下得出的模型表达式均有较好的回归效果且精度较高（表3）。由表3可知，两种模型的RMSE均小于刘秉正公式（0.12），其中处理二所得误差公式与包含植被覆盖度的因式结合所得模型RMSE最小，表明其模型的预测精度最高。同时也表明，在植被覆盖度作为关键因子的前提下，添加株高、结皮厚度与糙度这三个调节因子来建立C因子模型是可行的，并且较单独采用植被覆盖度预测C值的结果更加精确，可为进一步完善C因子模型提供思路。

表3 模型评价Table 3 Model evaluation

3 讨 论

现有的研究成果中，有大量关于植被覆盖度与C值的计算公式，关系模型的形式也各有不同，有指数形式、对数形式等等。刘宝元在植被覆盖度的基础上，将株高纳入了计算模型，并且考虑了群落层次结构，使C值的计算更加科学合理。但植被覆盖度与株高只是表征地表作物覆盖的指标，并未体现管理措施对土壤流失的影响。正是以此为启发，本研究尝试考虑更多对C值有影响作用的因子，共同拟合C值，建立计算C值更精确的预测模型。

作物种植覆盖地表，能有效削减雨滴能量，截留一定的降水，并且作物秸秆能够阻滞径流，甚至改变径流状态，减缓径流流速，起到增加土壤入渗，减少冲刷的作用；其次，作物生长发育过程中的人为管理虽然会扰动地表土壤，但同时又会形成高低不一、大小不等的微地形，从而提高地表粗糙度，利于水沙停积，也起到了减轻土壤侵蚀的作用。因此，将植被覆盖度作为关键因子，株高、结皮厚度、地表糙度作为调节因子共同建立C因子模型，理论上可以提高精度。实际上，本研究得到的C因子计算模型的RMSE仅为0.089，较最接近实测C值的刘秉正公式的RMSE（0.12）更小，精度更高。

本文在建模方法上对比已有学者关于植被覆盖度与C因子的不同模型，选择模型预测值与本研究实测C值最接近的模型（刘秉正公式）。以刘秉正公式中含植被覆盖度因子的因式类型及系数作为本研究中关键因子即植被覆盖度加入模型的基本形式，然后以两种形式（加、乘）纳入调节因子去逼近误差。得出的模型RMSE较刘秉正公式小。这里建模的整体思路是以不同形式（加、乘）加入调节因子（结皮、糙度和株高）对仅通过关键因子（植被覆盖度）计算C值进行修正，提出一种新的模型。后期可将试验设计进一步细化，如通过设置坡面处理为作物地+非结皮与作物地+结皮，可对比分析结皮对C值的影响，以此类推设计试验，分析不同单因子对C值的影响，再探讨复合因子，如结皮和糙度共同作用对C值的影响，从而分层递进式研究C因子的计算，使C因子模型更加精确。

本研究也存在可改进之处。首先，研究对象为单一作物，若能将多种作物综合对比，对作物覆盖与管理因子的研究会有更大促进作用，这也是下一步要进行的研究；其次，本试验为小区试验，数据有限，后期结合大田试验数据则能更好反映问题。

4 结 论

我国作物坡地C因子研究整体缺乏一定的系统性，虽有大量利用植被覆盖度计算C值的公式，但植被覆盖度只是表征地表作物覆盖的指标之一，并无体现出管理措施对土壤流失的影响，且建模方法也多是直接进行回归分析，因此还需进一步强化研究。本研究通过室外人工模拟降雨，以大豆为研究对象，划分五个生育期进行试验。以植被覆盖度作为关键因子，以株高、结皮、地表糙度作为三个调节因子分步进行建模。先确定关键因子主体结构，再采用调节因子去逼近误差项，对仅利用植被覆盖度计算C值进行修正，分步得出C因子模型。本研究C因子体现大豆作物植被覆盖及其管理措施对土壤侵蚀的综合影响，但决定C因子的诸多因素还有待深入研究，且研究广度需拓宽至多种作物。要推广完善C因子模型，无论是因子的选取还是建模的方法均需要进一步思考和研究。