广义限制的P-限制半群

晏 潘，王守峰

云南师范大学 数学学院，昆明 650500

众所周知，逆半群是半群代数理论研究中最受重视的半群类，其研究成果极为丰富(可参见文献[1-2]).自20世纪70年代起，逆半群的一些推广形式得到半群研究者的重视.作为逆半群在正则半群中的一种推广，文献[3]提出了正则*-半群.随后，正则*-半群成为20世纪70年代到90年代的研究热点之一，许多著名的半群学者对此类半群进行了研究(参见文献[4-7]).

特别地，文献[6]研究了一类特殊的正则*-半群(即广义逆*-半群)的代数结构和自由对象.与此同时，作为逆半群在非正则半群中的推广，限制半群也得到了充分研究，取得了较丰富的成果(参见文献[8-9]).为了给出正则*-半群和限制半群的共同推广形式，文献[10]引入了P-限制半群.当前，P-限制半群类及其子类受到了半群工作者的充分关注(见文献[11-16]).

本文的目的是对一类P-限制半群(即广义限制的P-限制半群)展开研究.这类半群是广义逆*-半群在P-限制半群中的某种对应，形成P-限制半群簇的一个子簇.本文利用左正规带与限制半群的拟直积给出了广义限制的P-限制半群的一个结构定理，并据此刻画了广义限制的P-限制半群这一半群类的自由对象.本文的结果改进和推广了文献[6]中关于广义逆*-半群的相关结果.

1 预备知识

设(S，·)是半群，+和*是S上的两个一元运算.据文献[10]，若对任意x，y∈S，下列等式成立：

则称(S，·，+，*)为P-限制半群，此时，称PS={a+|a∈S}={a*|a∈S}为S的投射元集.P-限制半群有如下一些基本性质：

引理1[10]设(S，·，+，*)是P-限制半群，x，y∈S，e，f∈PS.则：

(1°)(x+y)+=x+y+x+，(xy*)*=y*x*y*；

(2°)x+(xy)+x+=(xy)+，y*(xy)*y*=(xy)*；

(3°)e+=e，e*=e，efRefe=(ef)+=(fe)*∈PS；

(4°)若eLf或eRf，则e=f.

据文献[10]，若PS是S的子半格，则称P-限制半群(S，·，+，*)为限制半群，类似于广义逆*-半群，若对任意e，f，g，h∈PS，有

efgh=egfh

(1)

则称P-限制半群(S，·，+，*)为广义限制的P-限制半群.显然，限制半群一定是广义限制的P-限制半群.但反之不然(见文献[15]中的例2.9).

据文献[11]，若P-限制半群(S，·，+，*)的投射元集PS生成的子半群CS=〈PS〉是S的子带，即S的任意有限个投射元的乘积均为幂等元，则称其为纯正P-限制半群.

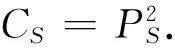
设S是纯正P-限制半群.在S上定义关系γ如下：

γ={(x，y)∈S×S|x+DCSy+，x*DCSy*，y+x=yx*}

其中DCS是CS上的格林关系.则有以下结果：

引理3[11]设(S，·，+，*)是纯正P-限制半群，a，b∈S，

(1°)aγb当且仅当a=a+ba*，b=b+ab*.特别地，当e，f∈PS时，eγf当且仅当e=efe，f=fef；

(2°)γ是最小的(2，1，1)-限制半群同余，且S/γ的投射元半格为

PS/γ={(aγ)+|a∈S}={a+γ|a∈S}={(aγ)*|a∈S}={a*γ|a∈S}={eγ|e∈PS}

引理4[1]设B为正规带，则：

(1°)B上的格林关系R是同余且商半群B/R为左正规带；

(2°)B是左正规带当且仅当它是左零带的强半格.

具体来说，若B是左正规带，则B上L关系是同余，且商半群Y=B/L是半格.设B的全体L-类为{Lα|α∈Y}.当α，β∈Y且α≥β时，定义

其中u是Lβ中任意元素.则B=(Y，Lα，ψα，β).

由等式(1)，容易验证以下结果：

引理5设(S，·，+，*)是广义限制的P-限制半群.则CS是正规带.

2 结构定理

本节的目的是利用左正规带与限制半群的拟直积给出广义限制的P-限制半群的一个结构定理.先介绍左正规带与限制半群的拟直积.

命题1设(S，·，+，*)是限制半群，L=(PS，Lα，φα，β)是左正规带.对∀(a，x，b)，(c，y，d)∈Q，在

Q=[L∶S]={(a，x，b)∈L×S×L|a∈Lx+，b∈Lx*}

上定义

(a，x，b)(c，y，d)=(aφx+，(xy)+，xy，dφy*，(xy)*)

(a，x，b)+=(a，x+，a) (a，x，b)*=(b，x*，b)

则(Q，·，+，*)是广义限制的P-限制半群，称其为左正规带L与限制半群S的拟直积.

证设(a，x，b)，(c，y，d)∈Q.则a∈Lx+，b∈Lx*，c∈Ly+，d∈Ly*.由引理1(2°)知(xy)+≤x+，(xy)*≤y*，故Q上定义的二元运算是合理的.此外，注意到x+*=x+，x*+=x*，x++=x+，x**=x*，Q上的两个一元运算也是合理的.

现设(a，x，b)，(c，y，d)，(m，z，n)∈Q.则

由上述事实及其对偶知(Q，·)是半群.

下证(Q，·，+，*)是P-限制半群.设(a，x，b)，(c，y，d)∈Q，由对称性，分以下几步证明：

步骤1 对S利用等式及引理1(3°)知x+x=x及x++=x+.故

步骤2 对S利用等式知(xy+)+=(xy)+.故

步骤3 对S利用引理1及等式，知x++=x+=x+*，(x+y+x+)+=x+y+x+=(x+y+x+)*=(x+y+)+.故

步骤4 对S利用引理1(3°)及等式和知x++=x+=x+x+=x+*.故

步骤5 对S利用引理1(3°)知x+*=x+.故

(a，x，b)+*=(a，x+，a)*=(a，x+*，a)=(a，x+，a)=(a，x，b)+

步骤6 对S利用引理1(3°)知(xy)++=(xy)+和x**=x*，而对S利用等式知(xy)+x=xy+x*.故

综上所述，(Q，·，+，*)是P-限制半群，且其投射元集为

设(a，x+，a)，(b，y+，b)，(c，z+，c)，(d，w+，d)∈PQ.则由S是限制半群知y+z+=z+y+，故

这就说明(Q，·，+，*)是广义限制的P-限制半群.

命题2任意广义限制的P-限制半群均(2，1，1)-同构于某个左正规带与某个限制半群的拟直积.

CS/R={Rx|x∈CS}={Rx+|x∈CS}={Re|e∈PS}

记L=CS/R并取Re，Rf∈L，其中e，f∈PS.则据引理3(1°)知：ReLRf当且仅当ReRf=Re；RfRe=Rf当且仅当Ref=Re；Rfe=Rf当且仅当efe=e；fef=f当且仅当eγf.由引理3(2°)，(S/γ，·，+，*)是限制半群，其投射元半格为Y=PS/γ={pγ|p∈PS}.对任意α∈Y，记Lα={Re∈L|eγ=α，e∈PS}.设Re，Rf∈Lα，e，f∈PS.则eγ=α=fγ.因此ReLRf.

下证映射

是S到[L∶S/γ]的(2，1，1)-同构.

设x，y∈S.若(Rx+，xγ，Rx*)=xφ=yφ=(Ry+，yγ，Ry*)，则Rx+=Ry+，xγ=yγ，Rx*=Ry*.据引理1(4)，有x+=y+，x*=y*和xγy，而利用引理3(1°)可得x=x+yx*=y+yy*=y.故φ是单射.

对任意(Re，xγ，Rf)∈[L∶S/γ]，有eγ=x+γ和fγ=x*γ.故

(exf)γ=(eγ)(xγ)(fγ)=(x+γ)(xγ)(x*γ)=xγ

由于

(xf)γ=(xγ)(fγ)=(xγ)(x*γ)=xγ

据引理3(2)°，有(xf)+γx+，进而由引理3(1°)知x+(xf)+x+=x+.由eγ=x+γ及引理3(1°)知ex+e=e.故由等式及引理1(3°)，(2°)知

(exf)+=(e(xf)+)+=e(xf)+e=ex+(xf)+x+e=ex+e=e

类似地，(exf)*=f.因此(exf)φ=(Re，xγ，Rf).故φ是满射.

设x，y∈S.注意到

R(xy)+∈L((xy)γ)+=L(xy)+γR(xy)*∈L((xy)γ)*=L(xy)*γ

由ψ(xγ)+，((xy)γ)+和ψ(yγ)*，((xy)γ)*的定义及引理1，有

此外，据引理1(3°)，有x++=x+=x+*.故

类似地，(xφ)*=x*φ.

结合命题1和2，得到本节的主要结果：

定理1同构意义下，广义限制的P-限制半群是且仅是左正规带和限制半群的拟直积.

3 自由对象

本节的目的是刻画广义限制的P-限制半群这一半群类的自由对象.为此，需要自由限制半群的相关概念和结论.

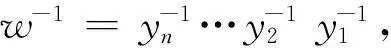
E={A⊆G|A有限非空，且对任意w∈A，都有w↓⊆A}

对任意g，h∈G，用gh表示g与h先连接再约简得到的约化字.由文献[1]，FIM(X)={(A，g)∈E×G|g∈A}关于下列二元运算和一元运算：

(A，g)(B，h)=(A∪gB，gh) (A，g)-1=(g-1A，g-1)

构成以({1}，1)为单位元的逆半群，其中gB={gw|w∈B}.易见FR(X)={(A，g)∈FIM(X)|g∈X*}{({1}，1)}是FIM(X)的子半群.据文献[8]，若考虑FR(X)上的一元运算+和*：

(A，g)+=(A，1) (A，g)*=(g-1A，1)

(A，1)≤(B，1)⟺A⊇B∀(A，1)，(B，1)∈PFR(X)

(2)

在L={(x，A)∈Y×E|x∈A}上定义二元运算如下：对任意(x，A)，(y，B)∈L，(x，A)(y，B)=(x，A∪B).则由文献[6]知L是左正规带.易知，对任意(x，A)，(y，B)∈L，(x，A)L(y，B)当且仅当A=B.记L(A，1)={(x，A)∈L|x∈A}.则{L(A，1)|(A，1)∈PFR(X)}就是L的全部L-类.当(A，1)，(B，1)∈PFR(X)，(A，1)≥(B，1)时，定义

(3)

其中(y，B)是L(B，1)中某元素.据引理4，有L=(PFR(X)，L(A，1)，ψ(A，1)，(B，1)).考虑拟直积

据命题1，([L∶FR(X)]，·，+，*)是广义限制的P-限制半群.设((x，A)，(A，g)，(y，g-1A))，((u，B)，(B，h)，(v，h-1B))∈[L∶FR(X)]，注意到

((A，g)(B，h))+=(A∪gB，gh)+=(A∪gB，1)

((A，g)(B，h))*=(A∪gB，gh)*=((gh)-1(A∪gB)，1)

及(3)式，有

(4)

((x，A)，(A，g)，(y，g-1A))+=((x，A)，(A，g)+，(x，A))=((x，A)，(A，1)，(x，A))

(5)

((x，A)，(A，g)，(y，g-1A))*=((y，g-1A)，(g-1A，1)，(y，g-1A))

下面的定理给出了非空集合X上的自由广义限制的P-限制半群的刻画.

定理2定义映射

则([L∶FR(X)]，i)是X上的自由广义限制的P-限制半群.

设x∈X.则xη=(xα，xπ，xβ)∈T=[M∶S].于是

xα∈M(xπ)+=M(x(εφ))+=M(({1，x}，x)φ)+=M({1，x}，x)+φ=M({1，x}，1)φ

对偶地，可知xβ∈M({1，x-1}，1)φ.故对任意y∈Y，都有yα∈M({1，y}，1)φ.设((x，A)，(A，g)，(y，g-1A))∈[L∶FR(X)].则1，x∈A.据(2)式知({1，x}，1)≥(A，1).由({1，x}，1)，(A，1)∈PFR(X)及φ是(2，1，1)-同态可知

({1，x}，1)φ≥(A，1)φ=(A，g)+φ=((A，g)φ)+({1，x}，1)φ，(A，1)φ∈PS

(6)

({1，y}，1)φ≥(g-1A，1)φ=(A，g)*φ=((A，g)φ)*({1，y}，1)φ，(g-1A，1)φ∈PS

(7)

下证σ是(2，1，1)-同态且iσ=η.设((x，A)，(A，g)，(y，g-1A))，((u，B)，(B，h)，(v，h-1B))∈[L∶FR(X)].据(4)，(6)式和(7)式知

另外，注意到((A，g)φ)+=(A，g)+φ=(A，1)φ及(5)式，有

类似地，(((x，A)，(A，g)，(y，g-1A))σ)*=((x，A)，(A，g)，(y，g-1A))*σ.故σ是(2，1，1)-同态.设x∈X.由x-1{1，x}={1，x-1}及εφ=π知

故iσ=η.最后证Xi能生成[L∶FR(X)].任取z∈X.则

zi=((z，{1，z})，({1，z}，z)，(z-1，{1，z-1}))

从而

(zi)+=((z，{1，z})，({1，z}，z)+，(z，{1，z}))=((z，{1，z})，({1，z}，1)，(z，{1，z}))

对偶可知

(zi)*=((z-1，{1，z-1})，({1，z-1}，1)，(z-1，{1，z-1}))

设((x，A)，(A，g)，(y，g-1A))∈[L∶FR(X)].则(A，g)∈FR(X).由FR(X)是自由限制半群知Xε生成FR(X).因此存在x1，x2，…，xn∈X，使得x1ε，x2ε，…，xnε在FR(X)的运算·，+，*下生成(A，g).根据[L∶FR(X)]中的运算，必存在a，b∈Y，使得x1i，x2i，…，xni可按照x1ε，x2ε，…，xnε生成(A，g)的方式生成元素((a，A)，(A，g)，(b，g-1A))(参考(4)式).若x，y∈X，则利用(4)式，1，x∈A及1，y∈g-1A，可得

类似可证其他情况.由以上讨论知Xi能生成((x，A)，(A，g)，(y，g-1A)).于是Xi能生成[L∶FR(X)].这表明满足iσ=η的σ是唯一的.故([L∶FR(X)]，i)是X上的自由广义限制的P-限制半群.