傅里叶变换耦合DNA编码的图像加密算法

史 进，蔡 竞，徐 锋

(1.浙江警察学院 现代教育技术实验中心，浙江 杭州 310053；2.浙江警察学院 刑事科学技术系，浙江 杭州 310053；3.浙江大学 信息技术中心，浙江 杭州 310058)

0 引 言

当前广泛研究的图像加密方法主要有两种：混沌加密[1-5]和光学加密[6-8]。如刘海峰等[3]利用两个超混沌系统输出一个无关联性的随机数组，然后将原始图像与其完成XOR运算，再将加密后的密文作为圆锥曲线加密的明文进行二次加密。Pan等[4]利用两个不同的Logistic映射来设计加密算法，通过设置两组初始条件，得到不同的随机序列，从而完成明文像素值的混乱与扩散。Guo等[5]利用3D位置乱方法来改变明文像素的位置，再借助Logistic-Fibonacci级联混沌系统的输出序来加密像素值。

但是上述方案也存在较大的缺陷，对此，研究人员提出了光学加密方案，如陈晓东等[6]利用迭代分数阶Chen混沌系统的随机序列来置乱明文图像，再借助量子细胞神经网络超混沌系统调制随机相位模板，再基于调制相位模板，利用Fourier变换来完成光学加密。但是该技术无法消除混沌周期性，导致其安全性有待提高。Zhou等[7]首先利用DRPE获取明文图像的相位信息，并量化生成认证信息，同时，利用CS对原始目标实施压缩，借助sigmoid图对CS完成量化，然后在量化测量中嵌入认证信息，通过置换和扩散得到密文图像。虽然该技术具有较高的信息认证安全性，但是，双随机相位编码所得到的频谱信息被完全保留在POMS中，导致其密文易出现轮廓问题[2]。Sun等[8]将相位图像加载到空间光调制器中，并将相位图像与振幅图像掩模结合，将其作为输入复振幅，借助Graytor变换与伽马分布相位掩码，对振幅进行加密。但是该方案忽略了明文数据，使其缺乏敏感性，且伽马分布相位掩码无法校准光轴，降低了密文的安全性。

为了增强加密系统的安全性，本文设计了分阶Fourier变换耦合DNA序列编码的光学图像加密算法。首先，根据DNA编码技术来处理图像，形成DNA序列矩阵。随后，将编码后的矩阵与另一个由Lorenz系统产生的混沌矩阵以及平面图像的Hash值进行XOR运算，得到混淆密文。迭代Lorenz系统，形成3个随机矩阵，采用不同阶数的Fourier变换，借助联合相位掩码对混淆密文进行级联光学加密。最后，测试了所提方法的加密安全性与敏感性。

1 DNA编码

DNA序列[9]主要含有A、C、G和T等4个碱基。在这4种碱基种，A和T，G和C是互补的[9]，如果将其应用到二进制基中，则00和11、10和00都是互补的。表1展示了24种编码准则，其中只有8种编码方案满足Waston-Crick补码准则[10]。

表1 8种DNA映射规则

在所提加密算法中，将明文图像视为3个矩阵：红R、绿G、蓝(B)，其中的每个像素均可表示为长度为4的DNA序列，例如，如果我们取红色矩阵中的一个像素值为173，将其转换为二值序列[10101101]，根据表1中的第1个规则，得到序列[10101101]。为了混淆明文像素，根据表2中XOR类型，对图像与密钥矩阵实施异或运算。

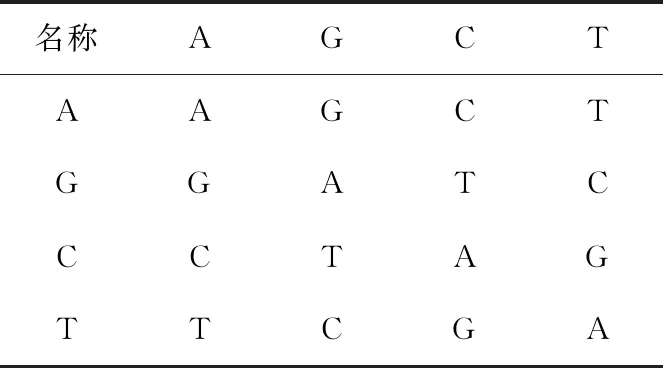
表2 DNA序列的XOR操作类型

2 所提的光学图像加密算法

所提的分阶Fourier变换耦合DNA序列编码的光学图像加密算法过程如图1所示。由图发现，其主要有两部分：①基于DNA编码的明文混淆；②基于混沌Lorenz系统与分阶Fourier变换的光学加密。通过采用DNA编码，将明文对应的DAN序列矩阵与混沌矩阵进行XOR运算，以有效消除混沌周期性，提高密文的抗破译能力。在加密过程中，采用了联合相位掩码，将其置于中间平面，并借助3次Fourier变换，实现明文的级联扩散，提高光电装置的光轴对准度。

图1 光学加密过程

2.1 基于DNA编码的明文混淆

设输入明文f(x,y) 的大小为M×N， 为了改善密文的敏感性，本文借助SHA-256散列函数[11]来生成图像的哈希元素值，以此作为一个256位的密钥K， 然后把它分割成32个子密钥ki

K=k1,k2,k3,…,k32

(1)

再根据式(1)来计算Lorenz系统的3个初值x0、y0与z0。 其中，Lorenz系统的模型[12]为

(2)

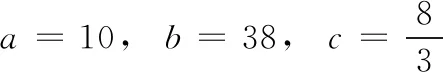
借助子密钥ki来计算x0、y0与z0

(3)

其中，x′0、y′0与z′0是用户给定的初始值。

令明文像素值组成的矩阵为P，并将其转换为一个M×8N维的二值矩阵Pbin，再根据表1，对Pbin进行处理，得到新的M×4N维的矩阵PDNA。同样地，将256位的密钥K转换为二值序列Kb，通过对其重复 [(M×8N)/32] 次，输出矩阵Mk。再采用相同的DNA编码规则，得到一个M×8N维DNA序列矩阵Mke。再根据表2中的XOR操作，对PDNA与Mke进行处理，形成混淆矩阵P0

P0=PDNAXORMke

(4)

最后，使用DNA编码规则，对P0实施解码，得到图像P1。

以图2(a)为例，设置x′0=10.003、y′0=6.009与z′0=20.001， 利用表1中的规则，根据上述过程，对其进行混淆，得到的解码图像如图2(b)所示。由图发现，经过DNA编码，明文的信息被有效混淆。

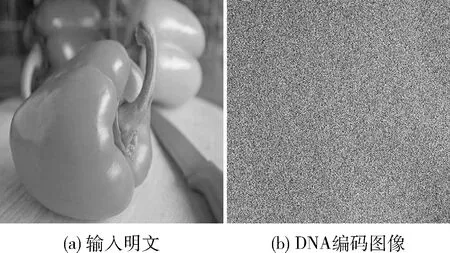
图2 基于DNA编码的明文混淆

2.2 基于混沌Lorenz系统与分阶Fourier变换的光学加密

根据式(3)得到的初值x0、y0与z0， 对Lorenz系统迭代100次，以消除瞬态效应，增强序列的随机性。随后，在此基础上，再迭代M×N次，输出3个序列 {(Xi),(Yi),(Zi)},i=1,2…M×N， 并通过设计量化函数，对 {(Xi),(Yi),(Zi)} 实施优化，消除局部单调性

(5)

再将3个新的序列 {(X′i),(Y′i),(Z′i)} 转换为3个矩阵X、Y、Z。在引入分阶Fourier变换[13]对X、Y、Z进行频域变换处理。分阶Fourier变换(fraction Fourier transform，FRFT)是一种时频分布，是经典Fourier变换的扩展板[13]。对于输入明文f(x,y)， 其Fourier变换为[14]

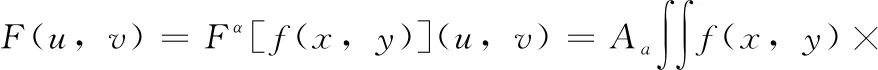
(6)

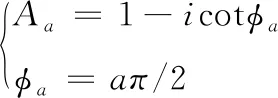
(7)

其中，F(u,v) 是Fourier变换；a是阶数；Aa是一个相位因子，取决于a值。

令K(x,y,u,v)=exp[iπ(x2+y2+v2)cosφa-2(xu+yv)/sinφa]， 则式(6)的逆变换为[14]

(8)

由文献[14]可知，FRFT的光学变换结构较为简单，由1-2个透镜来实现光学处理。在借助FRFT来完成输入信号的频域变换时，通常需要将一个掩码置于透镜前面。而普通的调制掩码容易引起光轴偏离问题，从而影响了加密过程中的光学干涉。为此，本文联合Fresnel波带[15]与Hilbert相位[16]来生成新的光学调制掩码。Fresnel波带自带一个光束聚焦环，可与光轴对齐，其模型如下[15]

(9)

其中，r是半径；f为焦距；λ是光束波长。

而Hilbert相位能够容忍一个pπ弧度的相对位误差，具备较好的光轴自动调整特性，其模型[16]为

H(ρ,θ)=exp(jpθ)

(10)

式中：p为Hilbert的阶数； (ρ,θ) 是极坐标

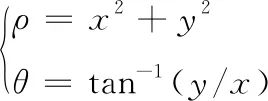
(11)

联合式(10)和式(11)，可形成新的调制掩码

(12)

再根据式(12)所示的掩码，通过式(6)与图3所示的光电装置，对解码图像P1完成光学干涉

图3 加密过程的光电混合装置

I(u,v)=Fa{P1exp[i2πR(r,φ)]}

(13)

通过式(13)的光学加密，可得到第一个变换密文I1。再将I1的像素值转换为对应的矩阵Q。随后，对X与Q进行XOR操作，得到过渡矩阵Q1

Q1=XOR(Q,X)

(14)

将Q1转变为对应的图像P2，借助阶数为β的Fourier变换，对其完成加密

I2(u,v)=Fβ{P2exp[i2πR(r,φ)]}

(15)

通过式(15)的加密，可得到过渡密文I2，将其转换为矩阵Q2。对Y与Q2进行XOR操作，得到矩阵Q3

Q3=XOR(Q2,Y)

(16)

将Q3转变为对应的图像P3，借助阶数为λ的Fourier变换，对其完成加密

I3(u,v)=Fλ{P3exp[i2πR(r,φ)]}

(17)

随后，将式(17)的输出密文I3转换为矩阵Q4。对Z与Q4进行XOR操作，得到矩阵Q5

Q5=XOR(Q4,Z)

(18)

根据上述的3次XOR操作与不同阶数的Fourier变换，可在图3中的输出平面上得到最终的加密密文I4。设置阶数a=0.76、β=1.32、λ=3.06，对图2(b)进行上述3次Fourier变换，形成的加密密文如图4所示。其中，经典的Fresnel波带与Hilbert掩码分别如图4(a)和图4(b)所示。二者形成的调制掩码如图4(c)所示。通过三次级联FRFT加密，得到的密文安全性越高，明文的视觉信息被充分隐藏，非授权访问者只能看到“噪声”内容，无法获取其真实的内容，如图4(d)～图4(f)所示，三者对应的熵值分别达到了7.976、7.989、7.997。

3 实验与分析

为了测试本文光学加密方案的优势，采用Matlab软件实施实验，并将安全性较高且较为新颖的技术作为对比组：文献[7]与文献[8]。产生调制掩码的经典光学参数为p=1,r=3,b=40mm,λ=632.8mm； 3个不同的Fourier阶数a=0.76、β=1.32、λ=3.06；以及混沌参数x′0=8.275、y′0=10.003与z′0=18.016。

3.1 光学加密效果

将图5(a)所示的彩色明文作为加密目标，借助上述3种技术对其实施光学干涉，输出的密文如图5(b)～图5(d)所示。对比这些密文发现，对于彩色目标而言，3种方法的输出结果均是彩色密文，且三者都可以较好地完成光学调制，且都没有视觉信息外泄，原始图像的内容被充分混淆，呈现一幅重度噪声图像。为了客观体现三者之间的优劣，本文统计了图5(a)～图5(d)对应的直方图，结果如图6所示。由数据发现，明文的直方图分布非常不均，很容易给攻击者留下破绽，如图6(a)所示。而所提算法的加密效果最佳，其直方图均匀分布最好，要优于文献[7]和文献[8]，如图6(b)所示。主要是所提算法采用了DNA编码技术来降低混沌周期性，且利用了新的调制掩码，提高了整个光学加密的光轴对准度，通过3次级联Fourier变换与XOR操作，充分破坏了加密系统的线性特征，显著提高了密文的抗破译能力。文献[7]则是采用CS方法与双随机相位编码来进行图像信息的光学加密，虽然其不受混沌周期性的影响，但其加密结果的频谱信息被完全保留在POMS，且其不能有效破坏线性关系，降低了密文的抗破译能力。文献[8]则是联合伽马分布与Graytor变换来实现图像的光学干涉处理，将明文分解为幅度图像与相位密文，但其进行Graytor变换的调制掩码无法校准光轴问题，影响了光学干涉过程，从而削弱了密文的安全性。

图5 3种算法的加密结果

图6 直方图测试结果(图中横坐标代表像素灰度等级，单位：级，纵坐标为灰度像素的个数，单位：个)

3.2 相关性测试

对于初始明文而言，其相邻像素间的紧密度是较高的，会给非授权访问者留下有用信息，给其破译加密系统带来一定的成功率，所以，光学加密方法输出的密文首先应该拥有非常低的紧密度[17]。首先，在明文与光学密文中随机确定3500对相邻的像素点，再借助式(19)对二者的紧密度Cxy完成估算[17]

(19)

以图5(a)和图5(b)为样本，根据上述过程，得到二者在Y轴上的Cxy分布结果，如图7所示。依据图7(a)中的像素分布发现，原始明文中任意两个相邻像素间的Cxy值都是很高的，而且所有的像素分布也是非常不理想，其中的像素都堆积成一条直线，此时的Cxy=0.9783。 但是经过光学干涉后的密文，其所有的像素分布情况比较良好，均匀遍历在整个灰度水平范围内，此时对应的Cxy很低，仅为0.0019，没有像素聚集效应，如图7(b)所示。

图7 Y轴方向上的Cxy测试结果

另外两个方向上Cxy统计结果见表3。观察输出结果发现，就明文而言，不管是哪个方向，其相应的Cxy都非常高，几乎解决最大值“1”，例如，其垂直方向的Cxy=0.9594。 但是经过光学干涉后，其3个方向上的Cxy值都非常低，几乎趋于“0”。

表3 3个方向的Cxy统计结果

3.3 敏感性测试

密钥敏感性是客观评价一个密文安全性的常用手段，即使破译密钥与正确密钥之间的误差非常小[18]，此时输出的解密结果仍然是错误的。根据这个原理，本次实验，验证了a=0.76的敏感性。首先，对进行a微小变动，剩余的密钥均维持不变，这样就形成了两组破译密钥a1=0.76+10-16、a2=0.76-10-16。再利用这些密钥对图5(b)实施解密，结果如图8所示。由破译结果发现，即使密钥出现了10-16这样细小的误差，非用户仍然是得不到正确的解密结果，如图8(a)～图8(b)所示。只有采用正确密钥对其复原时，才可获取完整清晰的明文，如图8(c)所示。另外，观察图8(d)可知，只有密钥误差为0时，对应的MSE曲线急剧下降，对应的MSE值接近0。这些数据显示了该方法拥有理想的敏感性，当未授权访问者所采用的密钥来出现微小变动时，其复原的结果与原始明文内容有着非常大的差异。

图8 密钥敏感性测试结果

3.4 抵御明文攻击能力测试

NPCR、UACI曲线[19]是客观衡量加密系统低于选择明文攻击强弱的经典指标，二者的计算函数为

(20)

(21)

(22)

其中，M×N为图像尺寸；I是初始图像的加密数据；I′是篡改I中的一个像素值后形成的新图像对应的加密数据。

把图5(a)当成本次实验的对象f，并将 (256,109) 处的像素值87篡改为78，以形成新的明文f′。再采用所提方法与其它两个对比组技术，对f与f′完成光学加密，输出对应的密文I、I′。随后，基于式(21)～式(22)，可形成不同算法的NPCR与UACI曲线，如图9所示。根据输出数据发现，所提加密方法的抵御明文攻击能力更为理想，其NPCR、UACI值始终是最大的，优于文献[7]和文献[8]，稳定值均超过了99.2%、35.6%。而文献[7]、文献[8]的NPCR、UACI值均低于所提方法。原因是本文算法利用明文来生成混沌系统的初值条件，使得生成的3个混沌矩阵均与明文相关，在三次级联Fourier变换与XOR操作过程中，都与明文内容紧密联系，从而增强了加密系统对明文变化的敏感性。文献[7]和文献[8]算法在整个加密期间，均与明文无关，导致其对明文内容变化不敏感，降低了密文的抵御明文攻击能力。

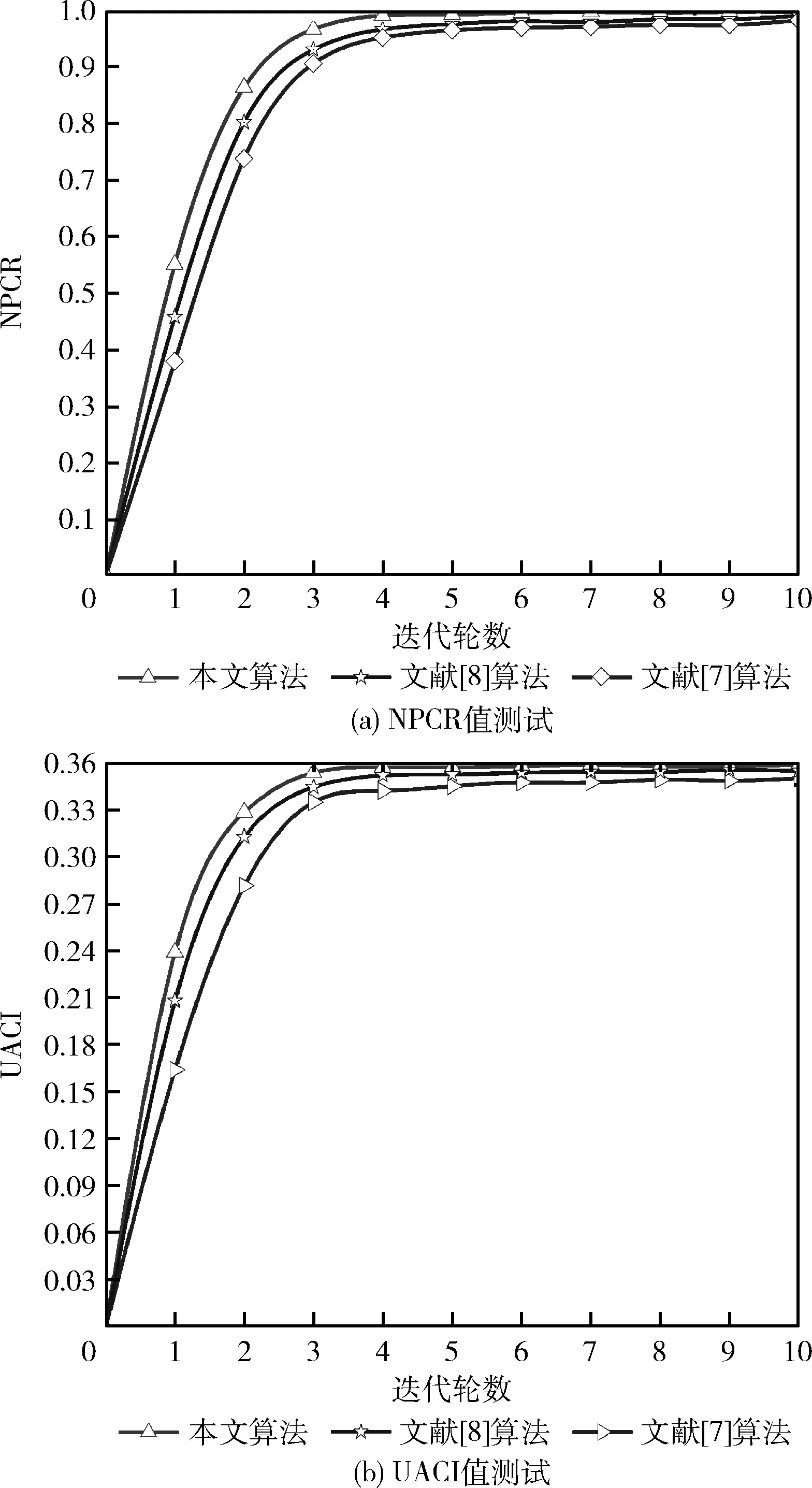
图9 抵御选择明文攻击能力测试

3.5 抵御剪切攻击能力测试

剪切攻击是目前评估加密系统的抗破译能力与稳健性的常用介质[1]。在本次测试中，把图5(b)～图5(d)当成实验样本，再把同等干扰程度的剪切攻击附加到三者上面，分别如图10(a)、图10(c)和图10(e)所示。随后，借助3种方法的逆过程来完成复原，获取的结果如图10所示。通过对比观察解密数据发现，当干涉密文受到未知的剪切攻击时，所提方案呈现出高度安全性与更好的稳健性，仍然可准确地对其实施复原，且输出结果较为完整，细节保持度较好，如图10(b)所示。但是，文献[7]、文献[8]两种技术的复原结果不理想，在遇到剪切攻击时，二者在一定程度上也能对其实施复原，但是效果不佳，图像较为模糊，而且细节保持度不高，和原始明文的相似度较低，分别如图10(d)和图10(f)所示。原因是所提方法联合了DNA编码与明文内容来完成图像的混淆，削弱了迭代周期性，而且还借助Fresnel波带与Hilbert函数来设计了新的调制掩码，通过三次级联Fourier变换与XOR操作，改善了整个光学干涉过程中的光轴对准度，增强了加密效果，充分破坏了加密系统的线性特征，显著提高了密文的抗破译能力，使得输出密文的像素分布均匀度较高，从而保证了剪切攻击下的复原质量。而文献[7]和文献[8]的技术都是借助普通的调制掩码来实现明文的光学干涉，无法解决光轴对准问题，导致加密不充分则，使其在剪切攻击下，难以准确复原图像。

图10 剪切攻击能力测试

4 结束语

本文通过使用分数阶Fourier变换、混沌系统与DNA编码，提出了一种光学加密算法。借助SHA-256方法来生成明文对应的密钥矩阵。通过DNA编码及其规则来处理初始明文，生成DNA序列矩阵，将其与密钥矩阵完成XOR操作，获取混淆密文。再根据明文对应的256位密钥迭代混沌Lorenz系统，输出3个随机序列，并将其转换为对应的混沌矩阵。联合Fresnel波带与Hilbert相位来建立一个新的调制掩码，将其置于透镜前，利用不同阶数的Fourier变换，联合3个混沌矩阵，在相应的光电结构中，对混淆密文进行级联光学加密，获取干涉密文。并对该方法进行了测试，输出数据显示其具备理想的加密安全，呈现出较强的抵御明文攻击能力。