基于粘结裂缝模型的混凝土受拉性能数值模拟

王 营，梁 力，李 明，赵 岐

(东北大学 资源与土木工程学院， 辽宁 沈阳 110819)

混凝土作为一种复杂的非均质复合材料。早期，学者[1-4]将骨料形状简化为球形，不考虑砂浆与骨料的交界面，仅将混凝土简化为砂浆与骨料并进行力学分析。为了更加全面的分析混凝土的力学性能，考虑砂浆与骨料间的力学性能，学者们又提出了更多的混凝土细观模型，如由Schlangen等[5]提出的格构模型，由Mohamed等[6]提出的M-H细观模型，由清华大学刘光廷等[7]提出的随机骨料模型等等，并在混凝土细观模型的基础上采用扩展有限元，双折线损伤本构等方法进行混凝土损伤断裂分析。

程一磊等[8]将骨料简化为正多边形来创建沥青混合料二维模型，开展三点弯曲试验，并结合扩展有限元，将试验结果与数值仿真进行对比。利用数值模拟与实验相结合的方式探究了沥青混合料在不同条件下的开裂行为，分析了骨料分布，初始裂缝位置对开裂行为的影响。王江等[9]应用蒙特卡罗方法，采用均匀化方法建立了混凝土多尺度均匀化数值模型。考虑骨料形状以及骨料分布的影响，得到细观混凝土的损伤以及应力应变曲线。田梦云等[10]，基于混凝土细观结构建立了混凝土的2D随机骨料模型，应用塑性损伤本构模型，模拟了混凝土在单轴拉伸和压缩载荷下的力学性能和裂纹的萌生扩展。

文献[8-10]中所采用的扩展有限元方法、均匀化方法以及塑性损伤本构模型应用较为广泛，但是，扩展有限元方法在处理非均质材料断裂过程中经常遇到数值奇异问题，均匀化方法以及塑性损伤模型只能显示单元损伤的位置，并不能模拟出宏观裂缝。相较于以上方法粘结裂缝模型能解决数值奇异问题，更好的模拟宏观裂缝发生扩展。目前，混凝土细观粘结裂缝模型由于需要自行编制粘结单元插入程序，所以应用相对较少。徐海滨等[11]采用单向拉伸模型，研究黏性界面单元的网格密度、圆形骨料分布及界面单元的断裂参数对混凝土应力-位移曲线的影响。刘永平等[12]采用粘结裂缝模型，证明微裂纹成核造成的初期损伤具有随机性与全场性，导致试样在峰值应力前出现非线性。董凡[13]采用粘结裂缝模型，将骨料形状假设为圆形，研究了骨料体积含量及试件尺寸对抗拉强度的影响，除此之外，还进行了三点弯曲、四点弯曲的数值实验。Li等[14]采用粘结裂缝模型，利用数字技术重构沥青混合料小梁，并进行了三维模型与二维模型断裂形态、荷载位移曲线以及能量释放进行对比。

以上粘结裂缝模型都采用单一的骨料形式，并未讨论骨料形状对于受拉性能的影响进行讨论，也没有对粘结裂缝数值模型砂浆与界面的细观参数进行统一的讨论。本文在有限元软件ABAQUS上，采用圆形、椭圆形、随机多边形三种骨料形式，建立混凝土细观粘结裂缝模型，进一步分析网格尺寸、骨料形状、细观参数即界面粘结单元断裂能、粘结强度，砂浆间粘结单元断裂能、粘结强度对于混凝土宏观力学性能的影响。

1 随机骨料生成

采用蒙特卡罗法建立二滩拱坝二级配混凝土平面细观数值模型[15]，混凝土模型平面尺寸取边长为150 mm的正方形，通过自编的随机骨料生成程序。骨料形状考虑圆形、椭圆形、随机多边形三种，其中各级配所对应的总面积相等，水工二级配混凝土的两种粒径为大石40 mm～20 mm与小石20 mm～5 mm，中石和小石骨料体积比例为45∶55，占总质量的50%。参考文献[9-13]中以直径12.5 mm与30 mm为代表粒径，生成细观混凝土，虽然与实际混凝土结构有一定差距，但可以满足计算与分析要求，通过瓦拉文公式，计算各级配骨料所占面积，大石所占面积为2 840 mm2，小石所占面积为3 940 mm2。取圆形骨料直径，椭圆形骨料长边为直径，随机多边形外接圆直径为代表粒径，各级配骨料个数不同，但是总面积相同，利用Python自编程序生成混凝土二维细观算法与模型，数值模拟整体流程如图1所示。骨料模型如图2所示。

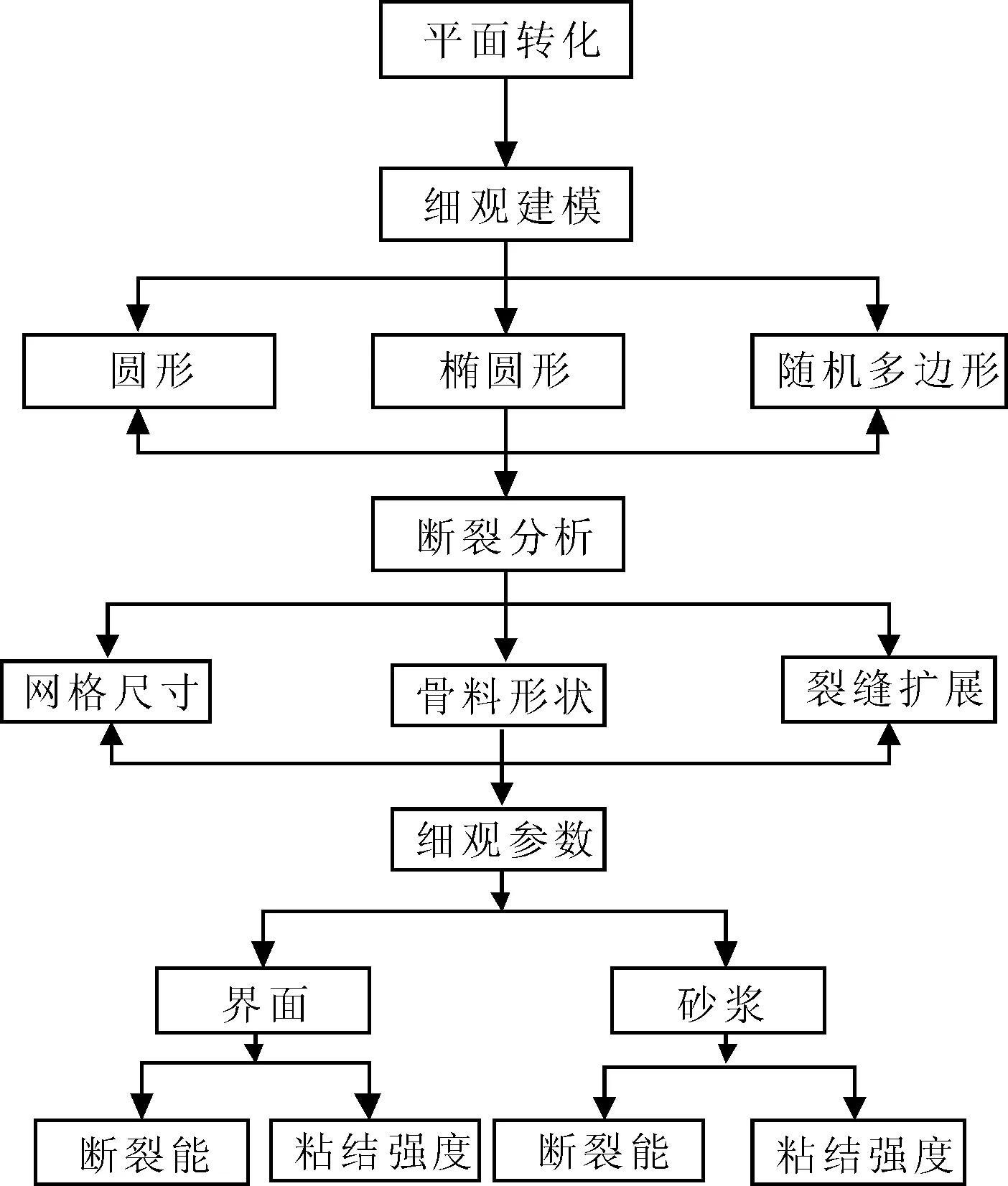
图1 数值模拟整体流程

图2 骨料模型

2 粘结裂缝模型

2.1 粘结单元

ABAQUS中的粘结单元采用了适用于模拟裂缝的牵引力-分离模型，其力-张开位移关系见图3。

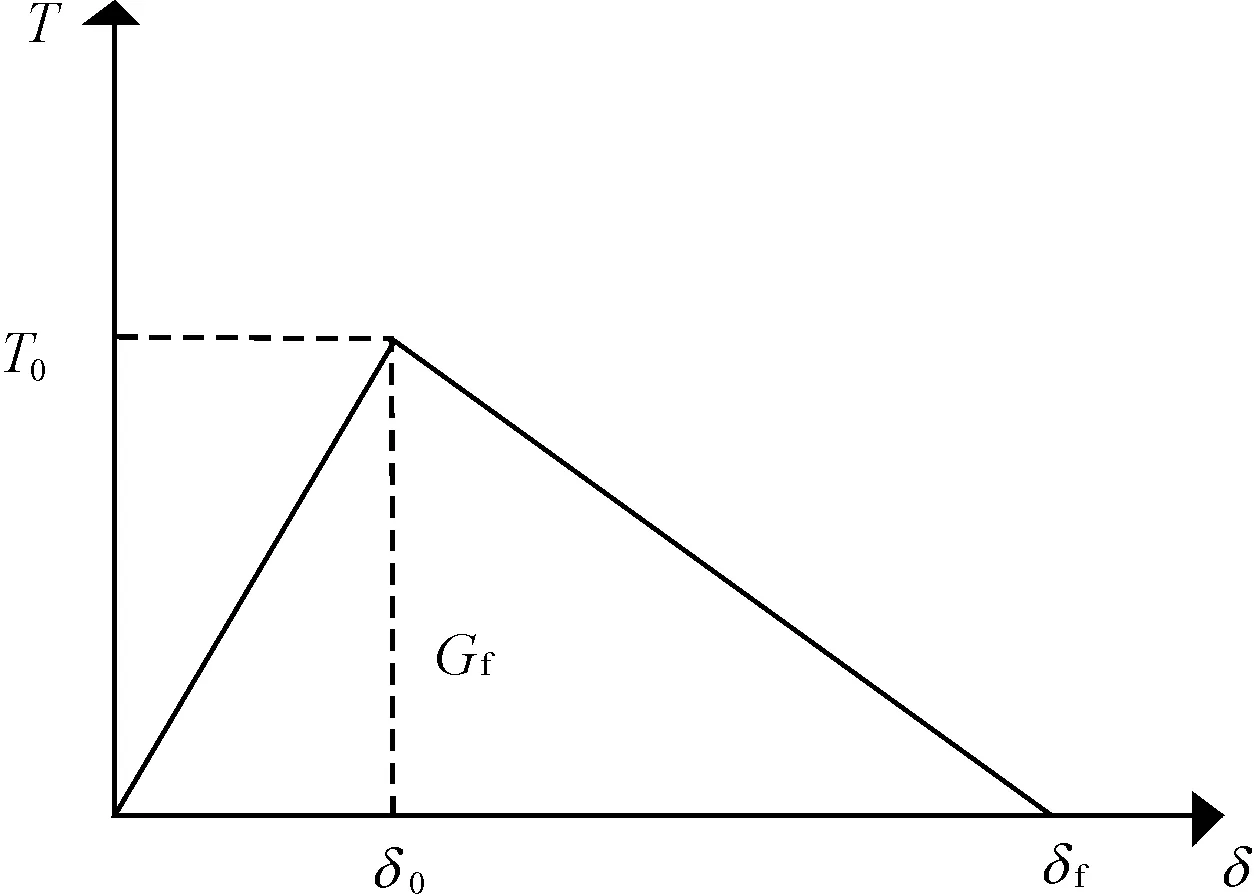
图3 力-张开位移关系

当裂缝尖端的拉应力小于混凝土的抗拉强度时，无裂缝产生，应力-位移线性增大；当达到混凝土的抗拉强度时，裂缝发生扩展，裂缝的扩展位移决定了裂缝面上传递应力的大小，峰值后的应力-位移曲线替代了应力-应变曲线的下降段，表现为张拉软化行为[11]。

图中Gf表示为断裂能，T0表示为材料的极限承载强度，即为粘结强度，这两个数值可以在实验室中测出。δf为材料的破坏位移，其中：

(1)

在未达到粘结强度T0时，其力-张开关系是线弹性的，材料表现出线性行为，当达到粘结强度以后，材料开始出现损伤，其损伤可以表示为：

(2)

式中：δm,max是加载历史中的最大有效相对位移；δm0和δmf分别为裂缝起裂和完全破坏时的有效相对位移；D为损伤变量，退化后的刚度KT可表示为：

KT=K0(1-D)

(3)

式中：K0为初始刚度矩阵。

本文选取二次名义应力准则作为开裂准则，当满足关系：

(4)

粘结单元出现损伤

式中：Tn和Ts分别为粘结单元的法向和切向应力；Tn0和Ts0分别为粘结单元的法向和切向的极限拉应力。〈〉是Macaulay括号。

2.2 粘结单元的嵌入

采用随机多边形模拟骨料，选择平面应力三角形单元，利用Python语言具有可操作性强的特点，通过ABAQUS建模导出的inp文件进行0厚度的Cohesive单元的插入，把整个细观混凝土分为开裂区、开裂区与非开裂区界面以及非开裂区，将砂浆视为开裂区，由于骨料的强度很大，通常情况下不开裂，所以将骨料视为非开裂区，两者界面视为最薄弱处。其步骤是：

(1) 记录单元、节点信息。

(2) 节点分裂，并重新编号。

(3) 生成Cohesive单元，区分界面与砂浆内部并将全部单元重新编号。

图4为插入Cohesive单元嵌入前后的示意图，图5为嵌入0厚度的粘结单元之后生成的混凝土细观粘结裂缝模型。

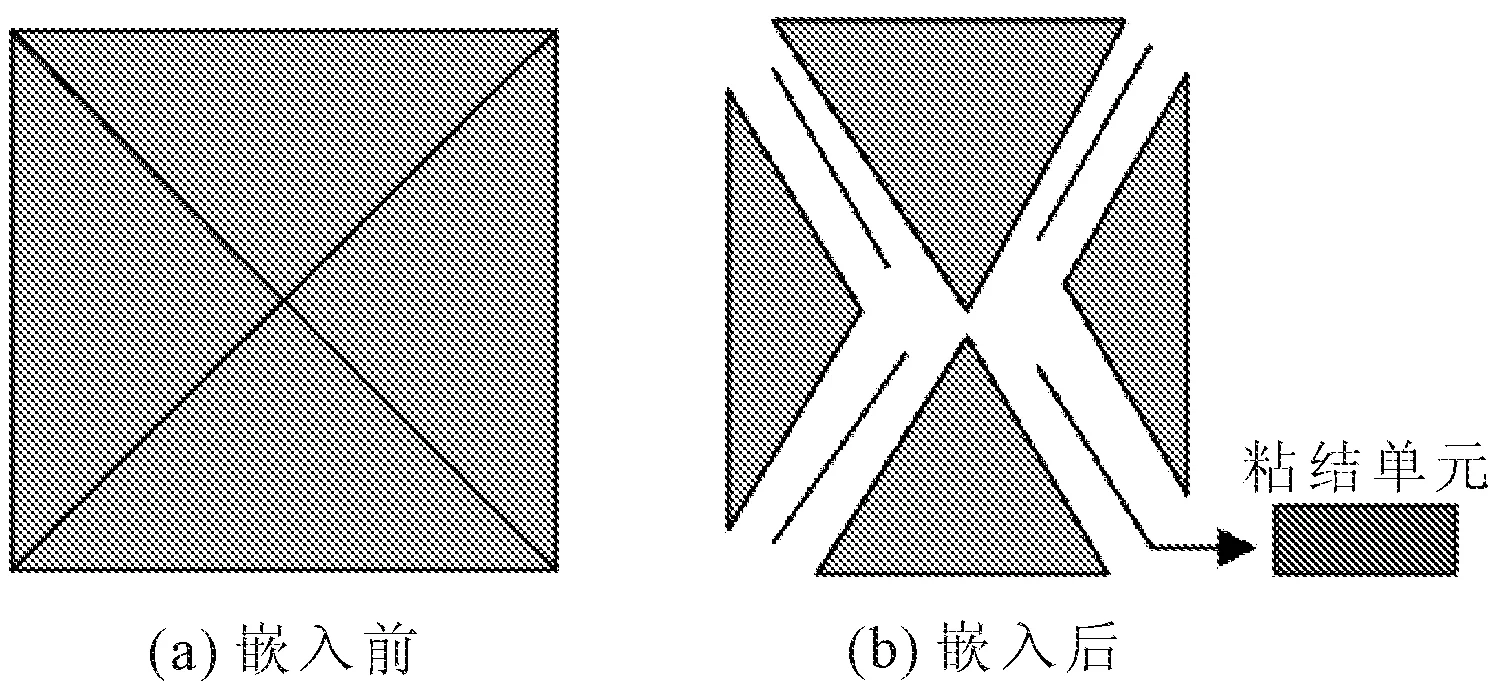
图4 粘结单元嵌入

图5 混凝土粘结裂缝模型

3 裂纹扩展及参数分析

3.1 力学模型

单向拉伸模型边长为150 mm的正方体，边界条件采用下部约束竖直方向位移，左下角约束左侧位移，左右两侧无约束，上表面施加垂直向上的位移荷载，计算模块采用ABAQUS/Stardand，力学模型见图6。

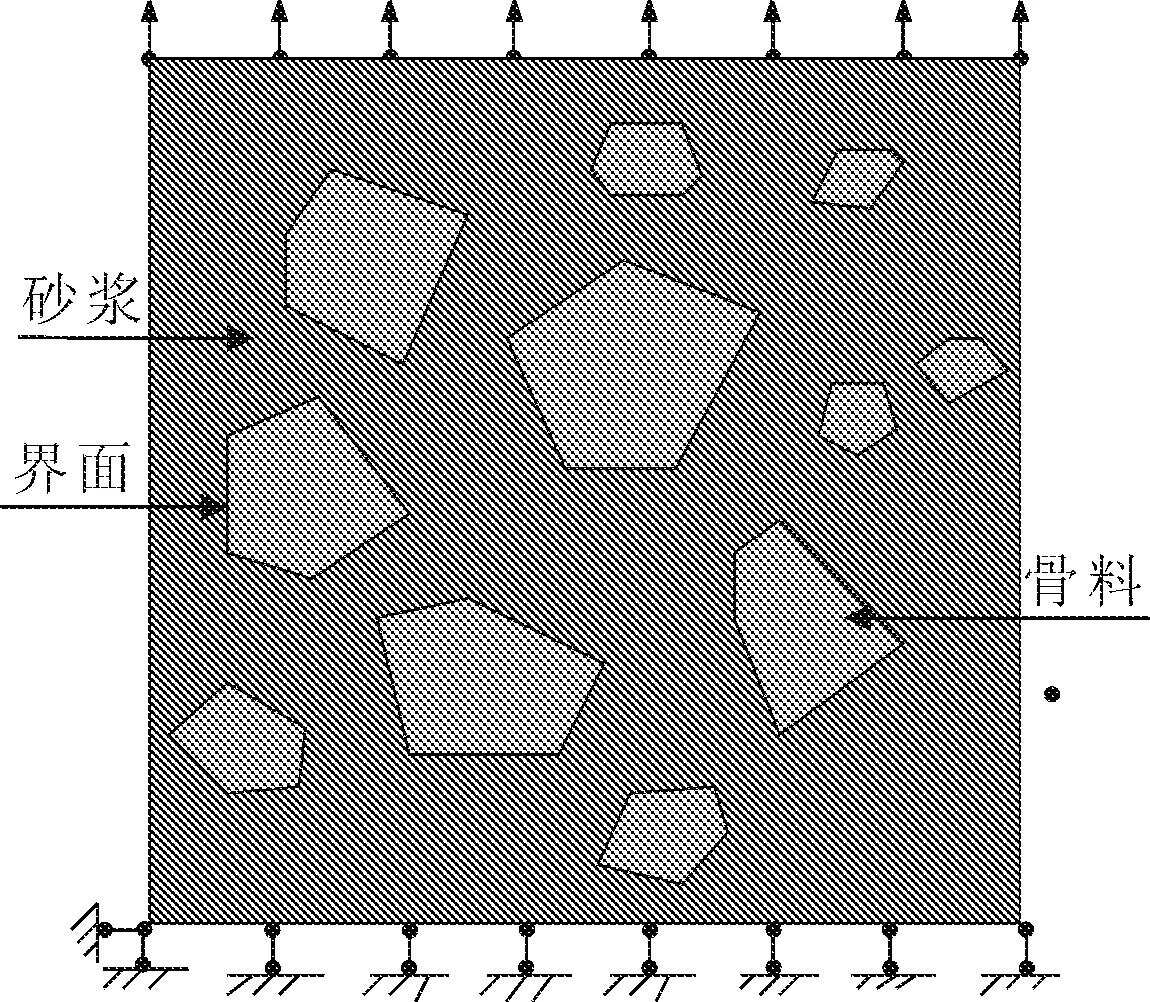
图6 单向拉伸模型

单向拉伸模型在各组分在达到各自的抗拉强度之前，应力-应变关系是线弹性的；当达到抗拉强度之后，采用线性应力-裂缝宽度关系来表征混凝土材料的软化力学行为[11]。采用二次应力准则，基于能量的线性软化的损伤演化方式，参考文献[11-13]并经过检验校核，选取参数，见表1。

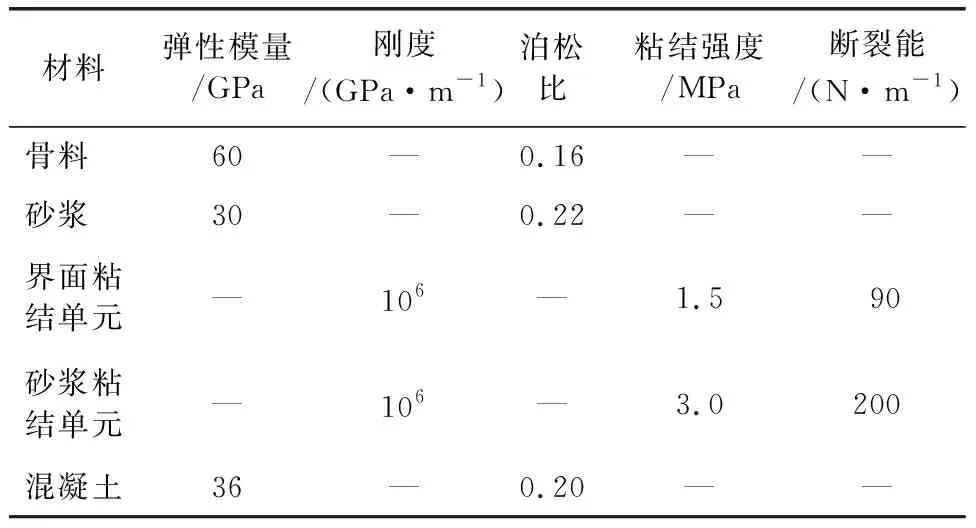
表1 力学参数

3.2 网格敏感性

生成骨料为随机多边形数值模型，网格的尺寸分为2 mm、3 mm、4 mm，生成三种不同的网格密度的有限元模型，图7中三个数值模型从左到右依次为3 140个实体单元，3 266个粘结单元；5 542个实体单元，5 510个粘结单元；12 346个实体单元，12 128个粘结单元；图8是对应图7中3种不同网格密度下的裂缝扩展形态，图9为三种网格密度下的应力-位移曲线。

图7 不同网格密度

从图8中可以看出，三种网格密度下裂缝位置稍有变化，破坏过程相同，都是围绕着中部骨料开裂，最开始界面发生开裂，后砂浆开裂，最后贯穿混凝土。

图8 不同网格密度裂缝扩展形态

图9是3种不同网格密度下获得的混凝土试件的应力-位移曲线，三者基本重合。抗拉强度为2.27 MPa、2.26 MPa以及2.27 MPa，数值模拟得到抗拉强度与文献[15]中的抗拉强度2.28 MPa，最小误差0.4%，最大误差0.8%。且3种网格密度获得的应力-位移曲线基本重合，可见粘结裂缝模型对于网格的依赖性很小。

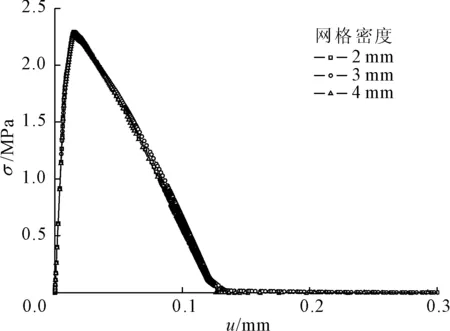
图9 不同网格密度应力-位移曲线

3.3 骨料形状

为考虑不同骨料形状的影响，建立了三组混凝土粘结裂缝模型数值试件，试件骨料形状为最理想的圆形、适合模拟卵石骨料的椭圆形以及模拟碎石骨料的随机多边形，其中每个级配的混凝土骨料的总面积相等，裂缝扩展形态以及应力-位移曲线如图10—图13所示。

图10 圆形骨料裂缝扩展形态

图11 椭圆形骨料裂缝扩展形态

图12 多边形骨料裂缝扩展形态

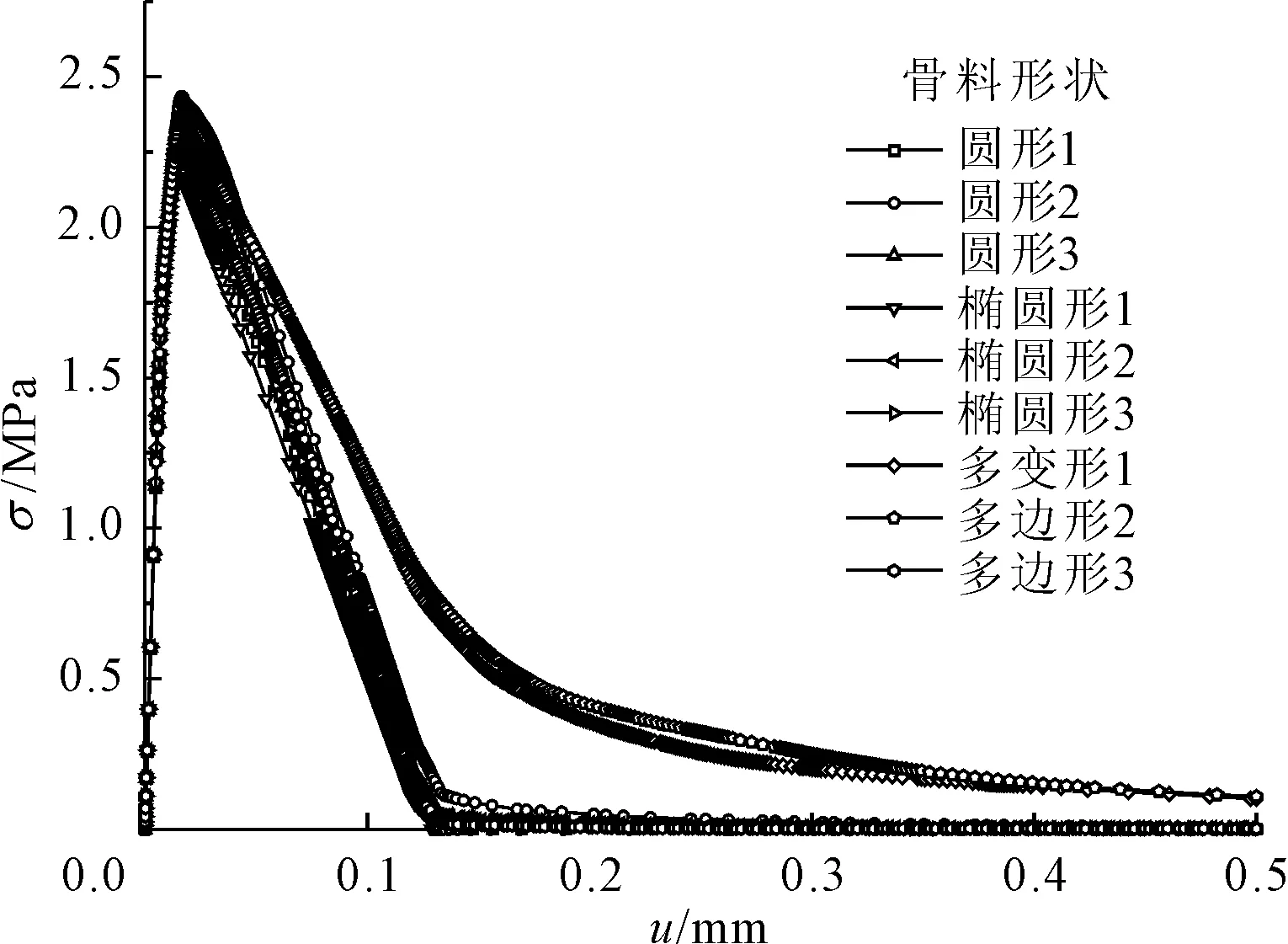
图13 三种形状骨料应力-位移曲线

由图10—图12可知，三种骨料的裂缝扩展形态都是自界面处首先发生，其次发生在砂浆之中，随着上部荷载的加大，最后裂缝连接成为一个整体，贯穿混凝土。裂缝扩展形态曲折，不再像均质模型一样，可以更好的模拟混凝土在单轴拉伸条件下的裂缝扩展形态。

由图13可知，圆形骨料的三个抗拉强度分别为2.31 MPa、2.43 MPa以及2.37 MPa。椭圆形骨料的三个抗拉强度分别为2.25 MPa、2.33 MPa以及2.26 MPa。随机多边形骨料的三个抗拉强度分别为2.33 MPa、2.37 MPa以及2.26 MPa。骨料的随机分布对于三种骨料形状的抗拉强度都有很大影响。圆形骨料平均抗拉强度为2.37 MPa，椭圆形骨料平均抗拉强度为2.28 MPa，随机多边形骨料平均抗拉强度为2.32 MPa。三种骨料形状平均抗拉强度最大的是圆形，其次是随机多边形，最后是椭圆形，最大相差3.8%，三种骨料的抗拉强度总体上相差很小。

随机多边形骨料的应力-位移曲线有两条包含面积明显大于椭圆与圆形，由此可见，由于骨料形状以及分布的随机性，虽然圆形、椭圆形、随机多边形三者抗拉强度相差不大，但是随机多边形骨料因为更加具有离散性，导致混凝土断裂耗能有时会比圆形、椭圆形明显增加。

3.4 细观参数分析

(1) 粘结强度。当断裂能确定时，分别改变砂浆间粘结单元和界面粘结单元的粘结强度，其应力-位移曲线分别见图14、图15。

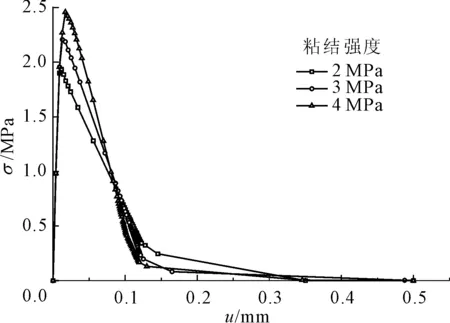
图14 砂浆间粘结单元粘结强度不同的应力-位移曲线

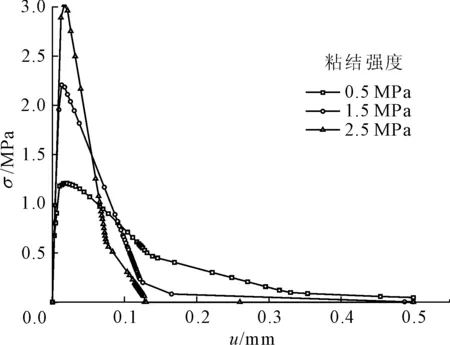
图15 界面粘结单元粘结强度不同的应力-位移曲线

由图14、图15可知，随着砂浆间粘结单元与界面粘结单元粘结强度的增大，混凝土材料的抗拉强度分别提高，应力-位移曲线在弹性阶段基本相同，但是应力-位移曲线在软化阶段展示出差异，粘结强度越大，软化阶段曲线的下降速率越快。

当界面粘结单元的粘结强度为1.5 MPa时，改变砂浆间粘结单元的粘结强度，混凝土单向拉伸的抗拉强度分别为：1.93 MPa，2.21 MPa以及2.46 MPa。

当砂浆间粘结单元的粘结强度为3.0 MP时，改变界面粘结单元的粘结强度，混凝土单向拉伸的抗拉强度分为1.21 MPa，2.21 MPa以及3.02 MPa。

总体来讲，粘结强度对于混凝土应力-位移曲线的影响主要集中抗拉强度与软化阶段，并且改变界面粘结单元的粘结强度较改变砂浆间粘结单元的粘结强度对于混凝土单向拉伸的抗拉强度与软化阶段更有影响。

(2) 断裂能。当粘结强度确定时，分别改变界面粘结单元以及砂浆间粘结单元的断裂能，其应力-位移曲线分别见图16、图17。

由图16、图17可知，随着砂浆间粘结单元断裂能与界面粘结单元断裂能的增大，应力-位移曲线在弹性阶段基本相同，抗拉强度大小无变化，在软化阶段表现出差异，随着砂浆间粘结单元断裂能与界面粘结单元断裂能增大，应力-位移曲线在软化阶段曲线的下降速率越慢。

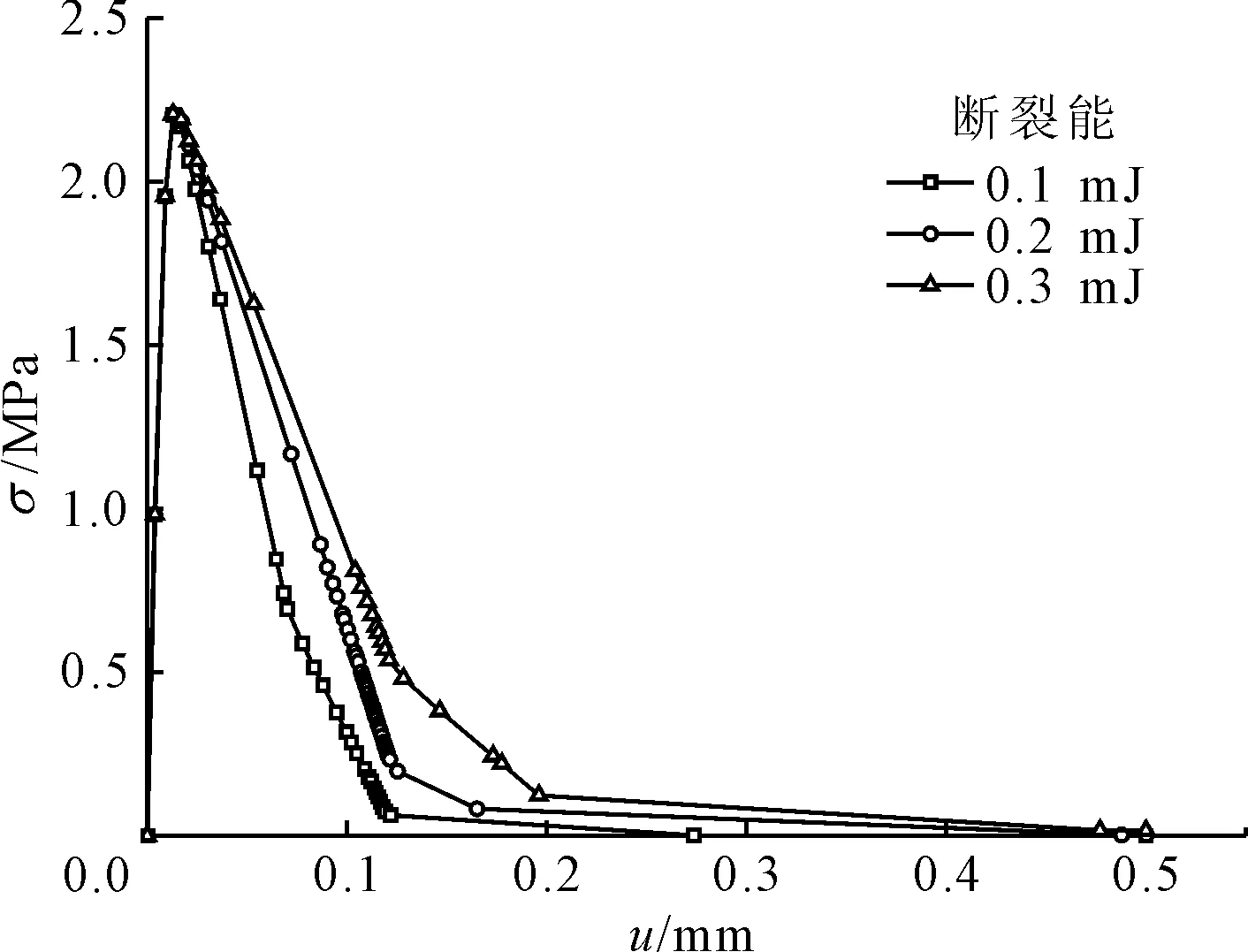
图16 砂浆间粘结单元断裂能不同的应力-位移曲线

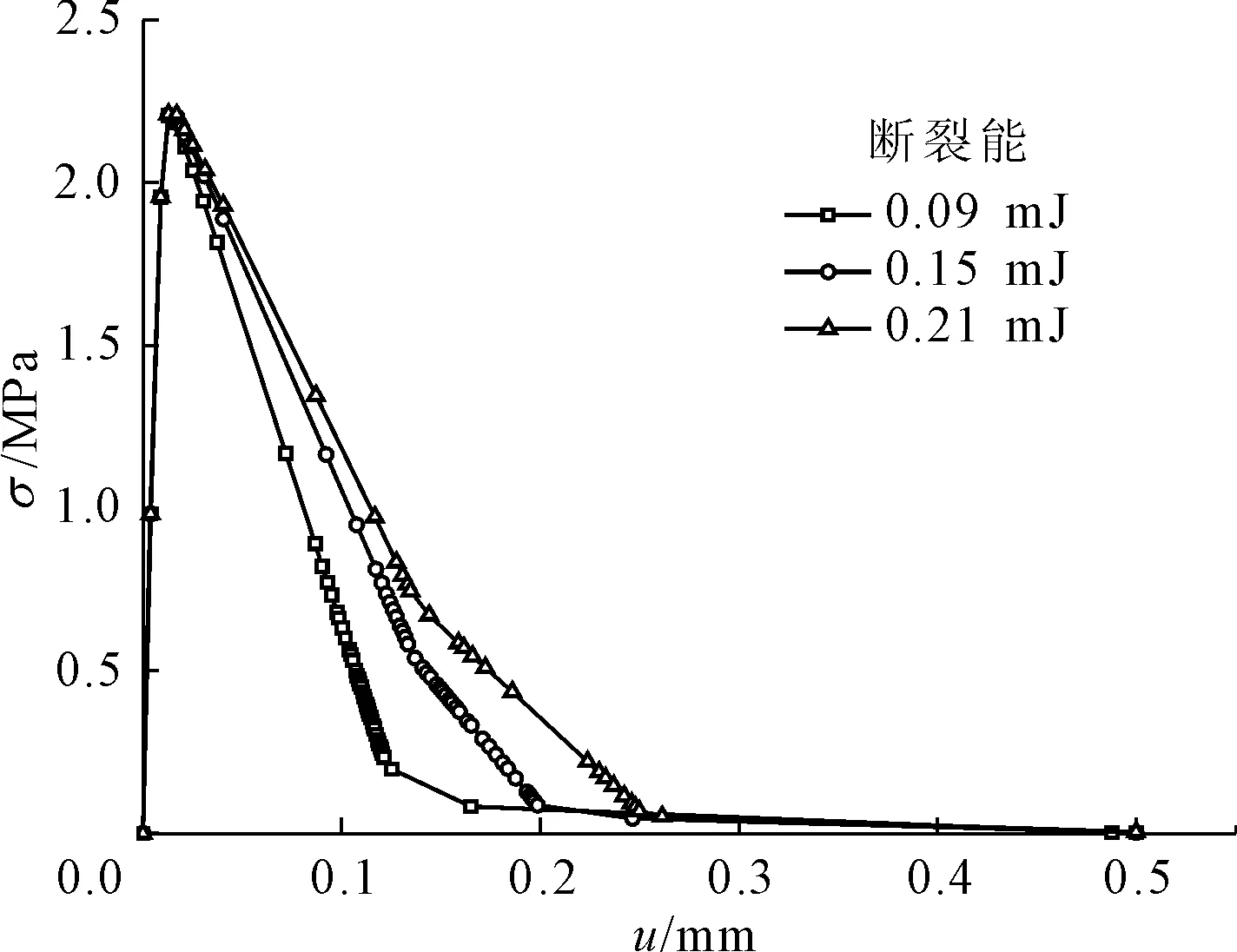
图17 界面粘结单元断裂能不同的应力-位移曲线

总体来讲，断裂能对于混凝土应力-位移曲线的影响主要集中在软化阶段，并且改变界面粘结单元断裂能较改变砂浆间粘结单元断裂能对于混凝土的应力-位移曲线的软化阶段更有影响。

4 结 论

(1) 通过自编程序生成混凝土细观粘结裂缝模型，建立的混凝土细观粘结裂缝模型在裂缝扩展形式、位置都与均质模型存在差别，更加接近混凝土实际裂缝扩展形态。混凝土细观粘结裂缝模型开裂位置具有随机性，裂缝扩展形态曲折，开裂位置起始于骨料与界面交界处，再向外扩展，然后贯穿混凝土。

(2) 网格尺寸对于粘结裂缝模型影响很小。

(3) 在含有相同骨料面积多边形、圆形、椭圆形骨料的数值混凝土模型中，三种骨料形状平均峰值应力最大的是圆形，其次是随机多边形，最后是椭圆形，但总体上差别很小。应力-位移曲线下降段也存在差异，随机多边形骨料耗能有时会明显大于圆形与椭圆形骨料。

(4) 当断裂能一致时，提升界面粘结单元以及砂浆间粘结单元的粘结强度都能提升模型的抗拉强度，改变界面粘结强度较改变砂浆间粘结强度对于模型整体抗拉强度影响更大。

当粘结强度一致时，改变界面粘结单元以及砂浆间粘结单元的断裂能对于模型抗拉强度以及弹性阶段几乎没有影响，断裂能越大模型的软化速率越慢，相同条件下，界面断裂能对模型软化阶段曲线影响比砂浆单元间断裂能影响要大。

(5) 通过对于砂浆间粘结强度、断裂能以及界面粘结强度、断裂能进行定性分析可知，界面单元的粘结强度和断裂能对混凝土的宏观力学性能有较大的影响，研究混凝土的力学性能时应优先考虑界面的影响，可为实际工程提供参考意义。